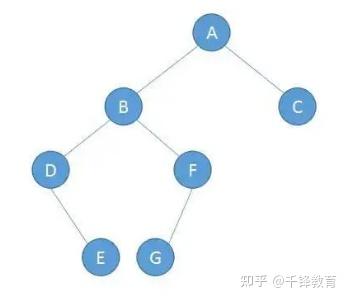
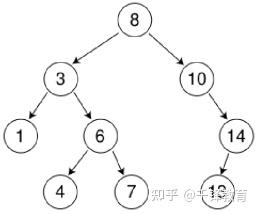
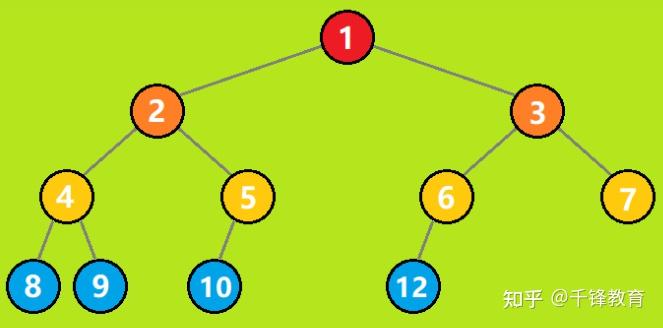
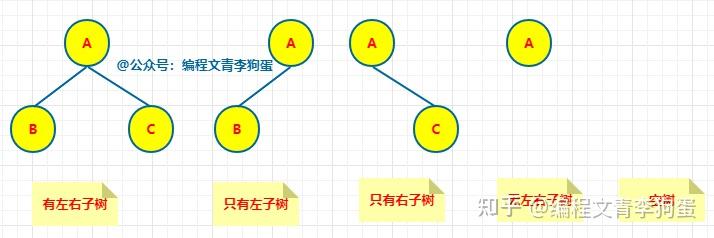
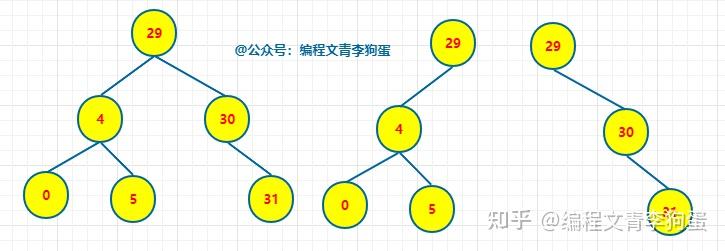
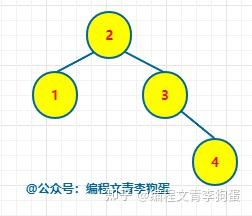
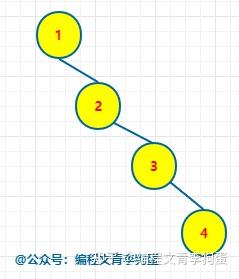
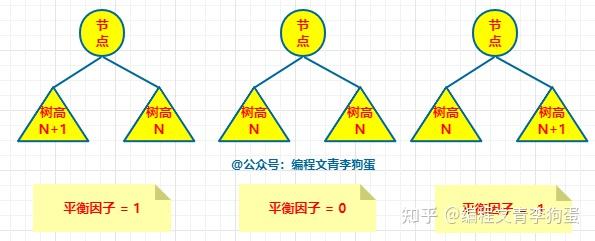
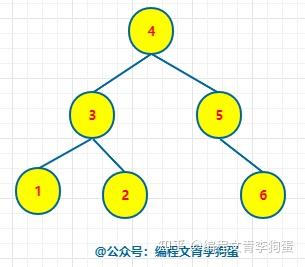
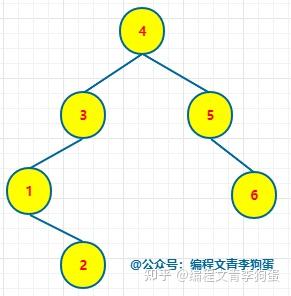
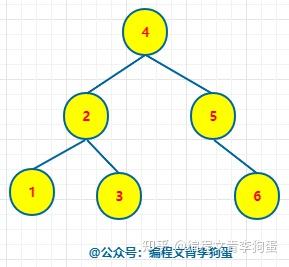
二叉树、二叉查找树、二叉排序树、二叉平衡树的区别是什么？ 二叉查找树又叫二叉排序树，也叫二叉搜索树，左节点小于根节点，右节点大于根节点。 二叉平衡树简称AVL树，比较追求高度平衡。 以上两种树都属于二叉树。 相关性质这里就不说了，可以参考这篇文章：二叉树、红黑树以及Golang实现红黑树 二叉树就是每个节点最多有两个子节点的树。它对节点的内容没要求。 二叉排序树 = 二叉查找树。它是一种二叉树，但是对节点内容有要求。每个节点的左子树（如果有的话）里所有节点的值都必须小于当前节点的值；每个节点的右子树（如果有的话）里所有节点的值都必须大于当前节点的值。 如果一颗二叉树看上去基本没有缺胳膊少腿（从根到每片叶子的路径长度最多相差1），那么它是棵平衡二叉树。对于一般二叉树而言，平衡不平衡没啥特别意义，但是对二叉查找树而言，越平衡则查找效率越高。 前言 首先感谢邀请。很荣幸，这些文章我都写过了，哈哈哈（真的不是为了推广自己写的文章，只是正好看到这个邀请回答的问题，而且又都会，很开心罢了）。 一、区别 二叉树：每个结点最多 2 棵子树，没有其它限制了。 二叉查找树：也叫 二叉搜索树，首先它是二叉树，并且 左子树上所有结点的值 小于 它根结点的值，右子树上所有结点的值 大于 它根结点的值。 二叉排序树：就是二叉查找树。 二叉平衡树：更加准确的应该叫 “平衡二叉树”，它是 “平衡二叉搜索树” 的简称。首先它是 “二叉搜索树”，其次，它是平衡的，即是它的每一个结点的左子树的高度和右子树的高度差至多为 1。 二、扩展阅读 1、二叉树 英雄哪里出来：二叉树 —— 用递归来描述数据结构 2、二叉搜索树 英雄哪里出来：二叉搜索树 —— 不能说完全没用，至少思想是经典的 3、平衡二叉树 英雄哪里出来：平衡二叉树 —— 如何优雅的进行旋转 4、二叉堆 英雄哪里出来：二叉堆 —— 数组 和 链表 的完美结合 废话不多说，让我们直接进入正题，让我们一起来看看二叉树、二叉查找树、二叉排序树、二叉平衡树的区别是什么吧！ 1. 二叉树 二叉树是一种特殊的树形结构，每个节点最多只有两个子节点。二叉树的特点如下： ● 每个节点最多只有两个子节点 ● 左子树和右子树是有顺序的 ● 即使只有一棵子树，也要区分左右子树
二叉树是每个节点最多有两个子树的树结构。通常子树被称作左子树和右子树。二叉树的定义如下： 二叉树的遍历方式有三种，分别是前序遍历、中序遍历、后序遍历。 2. 二叉查找树二叉查找树，又名二叉搜索树、二叉排序树，它或者是一棵空树，或者是具有下列性质的二叉树：
● 若它的左子树不空，则左子树上所有结点的值均小于它的根节点的值； ● 若它的右子树不空，则右子树上所有结点的值均大于它的根节点的值； ● 它的左、右子树也分别为二叉查找树。 二叉查找树的实现代码如下： 3. 二叉排序树
二叉排序树（BST）是一种特殊的二叉树，它的每个节点都满足左子树上所有节点的值都小于该节点的值，右子树上所有节点的值都大于该节点的值。BST的特点如下： ● 左子树上所有节点的值都小于该节点的值 ● 右子树上所有节点的值都大于该节点的值 ● 左右子树都是BST 二叉排序树的实现代码如下： 二叉排序树的遍历方式同二叉树，即前序遍历、中序遍历、后序遍历。 4. 二叉平衡树 二叉平衡树是一种特殊的二叉排序树，它的每个节点的左右子树高度差不超过1。二叉平衡树的特点如下： ● 每个节点的左右子树高度差不超过1 ● 左右子树都是平衡二叉树
二叉平衡树的实现代码如下： 二叉平衡树的遍历方式同二叉树，即前序遍历、中序遍历、后序遍历。 5. 总结 二叉树、二叉查找树、二叉排序树、二叉平衡树都是树结构的一种形式，但是它们在实现和使用上有很大的区别。二叉查找树和二叉排序树都是基于二叉树的基础上进行了优化，可以更快速地查找特定的数据。而二叉平衡树则是为了解决二叉查找树在极端情况下退化为链表的问题而提出的，它保证了每个节点的左右子树高度差不超过1，使得树的高度始终保持在O(log n)的级别。因此，在不同的场景下，我们要根据自己的需求选择不同的树结构来实现哦。 最后给大家把二叉树、二叉查找树、二叉排序树、二叉平衡树他们之间的区别给大家做一个汇总，这样方便大家总结学习： ● 二叉树是一种树状数据结构，每个节点最多有两个子节点。其中，根节点没有父节点，叶子节点没有子节点。二叉树可以为空树。 ● 二叉查找树（BST）是一种二叉树，它满足以下条件：若左子树不为空，则左子树上所有节点的值均小于它的根节点的值若右子树不为空，则右子树上所有节点的值均大于它的根节点的值左右子树均为二叉查找树没有键值相等的节点 ● 二叉排序树（BST）和二叉查找树（BST）是同一个概念，是一种二叉树，满足二叉查找树的条件。 ● 二叉平衡树（AVL）是一种自平衡的二叉查找树，它满足以下条件： 左子树和右子树的高度之差不超过1 左右子树均为二叉平衡树 总结一下，二叉树是一种树状数据结构，每个节点最多有两个子节点。二叉查找树和二叉排序树是同一个概念，它们是一种满足特定条件的二叉树。二叉平衡树是一种自平衡的二叉查找树，它保证了树的高度平衡，防止树失衡过深。 对于“二叉”各种类型的树我可是太熟了，下面我就来给大家好好讲一下！ 首先来看「二叉树」。 二叉树，表面上看上去是有“两个叉的树”，这样应该不准确，这上面还得加个限制条件：最多。 每个节点最多只有两个叉的树叫二叉树 既然是最多，那对于每个节点来说，可以一个叉，也可以没有叉，所以像下图这些都是二叉树。
ecsrm-10 上面 5 种包括了二叉树的所有基本形态。 除了上面讲的基本形态，还有很多特殊的二叉树：二叉查找树、二叉排序树，二叉平衡树。 其实「二叉查找树」和「二叉排序树」它俩是同一个树，我更喜欢称它们为「二叉搜索树」，前面俩算是它的别名。 见名知意，从它的别名可以看出，二叉搜索树是有数值的树（不然怎么排序呢），且有序（不然干嘛排序呢）。 既然有数且有序，肯定有合乎这俩的性质。 二叉搜索树有以下的性质：若左子树不空，那左子树所有节点的值均 < 根节点的值。若右子树不空，那右子树所有节点的值均 > 根节点的值。左右子树也均为二叉搜索树。
下面再来讲「平衡二叉树」，在这呢，我就先透漏一下平衡二叉树的半个概念，它和二叉搜索树有点关系：平衡二叉树也是一棵二叉搜索树。 那现在可能又有一个疑问，为啥有了二叉搜索树还要脱裤子放屁整出个平衡二叉树？ 那就得从盘古开天辟地，呃，从二叉搜索树的一个特殊情况说起… 如果你看过我二叉搜索树的实战文章，在分析递归题解时间复杂度的时候我一般会说：xx 大小取决于二叉搜索树的高度，二叉搜索树最坏情况下的高度为 n。 问题就出在这个高度为 n 上。 比如对于序列 root = [1,2,3,4]，正常情况下，我们构造的应该是下面这样的：
但总有不正常的时候，比如在老年痴呆的的情况下构造出的二叉搜索树可能是下面这样的：
你看这像啥样子，好好一棵二叉搜索树非得 cos 个”单链表“。 这就造成了，本来我查找一个节点的时间复杂度度是 O(logn)，现在硬生生的成了 O(n)。 比如我正常情况下找 4 这个节点，找 2 次就够，而在 cos 情况下，我得找 4 次，这种现象就是二叉搜索树的退化。 从上面两张不同二叉搜索树的图可以看出，树的高度决定了它的查找效率，那我们是不是可以这么考虑：当树的高度最小时，就能够保证树的查找效率。
连我都能考虑出来的东西，显然大佬们早就解决了，当然了也没很早，也就区区…60 年叭~ 1962 年，两个数学家 AV + L 提出了平衡二叉树的概念。 哎呀妈呀，终于套上了，至于平衡二叉树到底是个什么东西，我们下…面分解。
我在上面说了平衡二叉树的半个概念，现在来把它补充完整。 平衡二叉树，是一种二叉排序树，其中对于每个节点的左右子树高度相差小于等于 1。 后半句点出了平衡二叉树中”平衡“的实际指向，即”高度平衡“！ 把二叉树左右子树的高度看成是左右子树的重量，把这两个重量放在天平上，尽可能保证这个天平是平衡的。
那怎么确定什么程度是”尽可能的平衡“呢？这里就引出一个概念：平衡因子（BF，Balance Factor）。 它的计算公式：平衡因子 = 左子树的高度 – 右子树的高度。 那对于平衡二叉树来说，它概念中”每个节点的左右子树高度相差小于等于 1“，这么来看，平衡二叉树的平衡因子只可能是 1，0，-1。
phecsrm1-9 也可以这么说，只要你的平衡因子的绝对值 > 1，那你就不是平衡二叉树。 由此，我们在判断一棵二叉树是不是平衡二叉树，2 个条件：这棵二叉树是二叉搜索树。这棵二叉树的每个节点的 BF 绝对值 < 1。 比如下图：
这就不是一棵平衡二叉树，它首先就不满足条件 1：是一棵二叉搜索树。 比如下图：
这也不是一棵平衡二叉树，它虽然满足条件 1 是一棵二叉搜索树，但是不满足条件 2，对于节点 3 来说，它的 BF = 2。 比如下图：
这就是一棵平衡二叉树，它同时满足条件 1 和条件 2。 平衡二叉树就通过这种“尽可能的平衡”，让树的高度保持在 logn，这是相对最小的树高，也正因为是维持了这个树高，对于一棵有 N 个节点的平衡二叉树来说，它每一个操作的时间复杂度都可以维持在 O(logn)。二叉树非递归遍历算法如何实现的？为什么说二叉树遍历用递归的方法不如非递归方法?算法学习中如何用递归函数求一个二叉树的高度？
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/28792.html
