硬件狗教你学电路【二】:电路分析方法 【硬件狗持续更新,两小时带你学完电路!】 目录: 一、电路模型与定理参考:邱关源《电路》第五版 章节【一】【二】【四】【五】 二、电路分析方法参考:邱关源《电路》第五版 章节【三】【十五】【十六】 三、电路动态分析方法参考:邱关源《电路》第五版 章节【六】【七】【十四】 四、正弦电路分析参考:邱关源《电路》第五版 章节【八】【九】【十】【十一】【十二】【十三】 五、非线性电路与均匀传输线参考:邱关源《电路》第五版 章节【十七】【十八】 上节回顾:硬件狗教你学电路【一】中我们解读了各种电路数学化的定理与建模的一般方法,通过该方法我们可以将电路里面的物理件转化为我们需要分析的数学问题,从而通过数学的语言来描述电路的状态,而不考虑其中的物理现象,真正实现“透过现象看本质”。 电路的组成主要包含两个要素:件和拓扑。本章的主要内容为分析电路的一般性方法 二、电路分析方法 对于一个电路而言,我们需要抽丝剥茧形成最简单的电路图,忽略电路各器件的组成,由最纯粹的节点和支路组成。在一般的教学过程中对电路的图一般解读不多,这就导致后面什么节点电压法,回路电流法,网孔电流法学得云里雾里,本篇文章中将重点解读下“电路的图”,对这些基本的图论有一定了解后面的方法自然就能够很好的理解了。总体的思路是:将具体问题抽象化(电路拓扑)以提高理解维度,然后再降低为低维度(电路支路)问题,从而对复杂电路进行一般性分析。这也是电路课程学习的主要意义:掌握一般性方法! 0、电路的图与树的概念 随着电路复杂度的提升,我们需要总结出一般性的电路分析方法,这里面涉及到大量的“图论”和“拓扑学”的相关知识,本文不展开讨论,但是了解其基本概念还是有利于我们对电路进行分析。对于一个电路而言需要将其电路的转化成如下的“抽象图”,称为电路的图,这种图包含了电路里面关键的两个信息:节点和支路。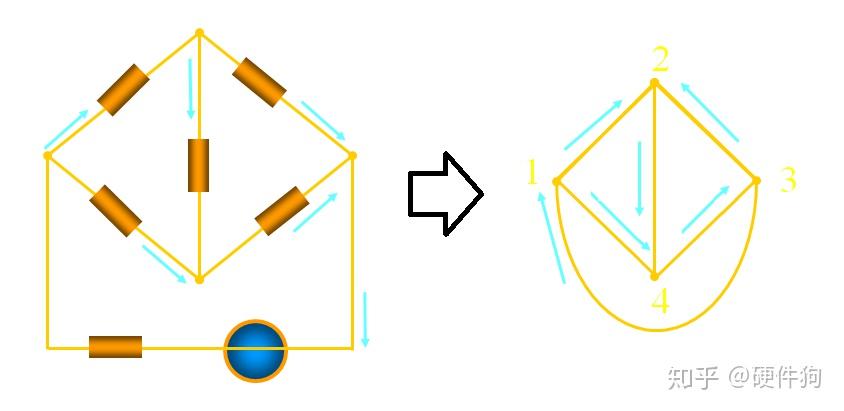
 电路的简化 对于一个电阻电路而言,两个节点之间的电路称为一条支路,每条支路拥有两个约束量:电压和电流,求解出每条支路的电压和电流即能够求解出整个电路的结果。比如对于一个电路,有n个节点,b条支路(支路数和节点数无关),该电路有2b(电压和电流)个未知量需要求取,如果能够列出2b个独立的方程组即能够完整地描述出电路状态。 那么重点问题是我们描述这个电路的方程应该怎么列? 1、 电路分析的方程解法 通过图论的分析,可以得到以下几个基本的规律: 对于电路中的n 个节点而言,在任意(n-1)个节点上可以得出(n-1)个独立方程数 对于电路中的回路列KVL可以得到b-(n-1)个独立方程数 对于电路中的支路可以根据VCR关系得到b个方程 因此,以上是一般性的方法获得2b个独立方程数,简称2b法 那么我们在分析电路的时候如何进行这些方程的选取呢? KCL方程很好列,任意选取(n-1)个节点即可得出KCL方程。这里因为将n个节点看做一个“大节点”那么其广义节点的电流和为零,因此只能获得(n-1)相互独立的KCL方程。 那么如何选取独立的KVL的回路进行列方程呢?对于一个电路而言,找到独立的回路数,是有一般方法的: 1、先在电路中找一个“树”(连通,包含所有节点,不含闭合路径),可以证明一个树包含的支路数为(n-1),那么剩下的支路数就是b-(n-1) 2、对于选定的“树”,再添加一条支路必然构成一个闭合回路(包含该支路),那么可以对该闭合回路列出其KVL方程,那么可以得到b-(n-1)个KVL方程,并且可以证明这些方程是相互独立的。 3、剩下添加进去VCR关系方程即可列出所有的电路方程
电路的简化 对于一个电阻电路而言,两个节点之间的电路称为一条支路,每条支路拥有两个约束量:电压和电流,求解出每条支路的电压和电流即能够求解出整个电路的结果。比如对于一个电路,有n个节点,b条支路(支路数和节点数无关),该电路有2b(电压和电流)个未知量需要求取,如果能够列出2b个独立的方程组即能够完整地描述出电路状态。 那么重点问题是我们描述这个电路的方程应该怎么列? 1、 电路分析的方程解法 通过图论的分析,可以得到以下几个基本的规律: 对于电路中的n 个节点而言,在任意(n-1)个节点上可以得出(n-1)个独立方程数 对于电路中的回路列KVL可以得到b-(n-1)个独立方程数 对于电路中的支路可以根据VCR关系得到b个方程 因此,以上是一般性的方法获得2b个独立方程数,简称2b法 那么我们在分析电路的时候如何进行这些方程的选取呢? KCL方程很好列,任意选取(n-1)个节点即可得出KCL方程。这里因为将n个节点看做一个“大节点”那么其广义节点的电流和为零,因此只能获得(n-1)相互独立的KCL方程。 那么如何选取独立的KVL的回路进行列方程呢?对于一个电路而言,找到独立的回路数,是有一般方法的: 1、先在电路中找一个“树”(连通,包含所有节点,不含闭合路径),可以证明一个树包含的支路数为(n-1),那么剩下的支路数就是b-(n-1) 2、对于选定的“树”,再添加一条支路必然构成一个闭合回路(包含该支路),那么可以对该闭合回路列出其KVL方程,那么可以得到b-(n-1)个KVL方程,并且可以证明这些方程是相互独立的。 3、剩下添加进去VCR关系方程即可列出所有的电路方程
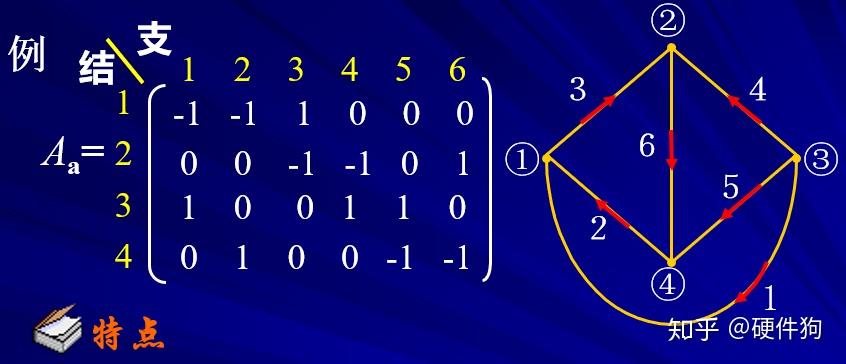
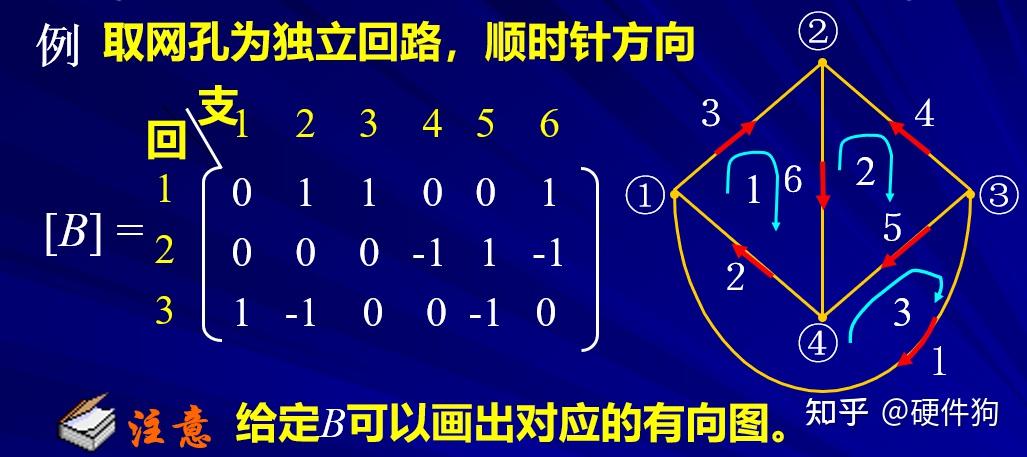
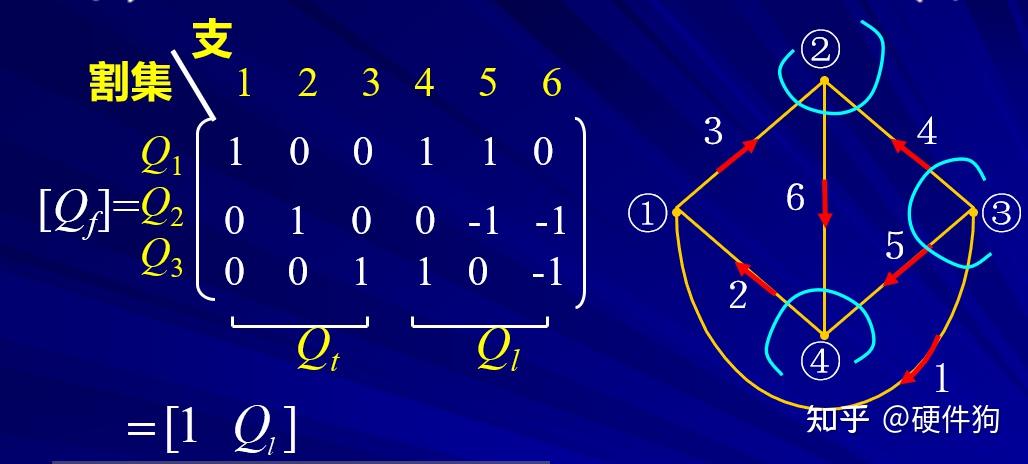
 电路拓扑中“树”的选取 通过以上的方法所获得KVL独立方程的方法,称为“支路电流法” 注意:支路电流法存在一种特殊的情况–网孔电流法,网孔电流法的适用范围仅适用于“平面电路”,也即是不能存在节点以外支路交叉的情况,网孔电流也是支路电流的一种特殊情况,因此不难看出网孔电流的个数为b-(n-1)。 支路电流法,网孔电流法,节点电压法,为一般的电路分析方法,在我们对一个电路进行方程选取过程中,通过对电路的观察尽可能多的获得已知量,从而简化方程复杂度,以下为一些常用的方程选取的一般性原则: 1、支路为独立电流源/电压源可以直接确定该条支路的电流/电压结果 2、选取合适的0电压参考点可以大大简化方程的复杂度 3、对于“平面电路”可以直接利用网孔电流法,而无需找“树”和“枝干” 当然,最最重要的是灵活应用基尔霍夫定律!!通过在电路图上局部列写基尔霍夫方程尽可能多的确定电路参数,对于不是太过复杂电路可以很快得出结果,但是因为由于没有进行独立方程的区分,可能会列出非独立的方程,使得局部电路方程无解,这样需要寻找更多非关联的信息来求取电路方程。 2、电路的矩阵形式 学过《线性代数》的我们知道,方程组的形式可以等效为矩阵的形式,将系数矩阵
电路拓扑中“树”的选取 通过以上的方法所获得KVL独立方程的方法,称为“支路电流法” 注意:支路电流法存在一种特殊的情况–网孔电流法,网孔电流法的适用范围仅适用于“平面电路”,也即是不能存在节点以外支路交叉的情况,网孔电流也是支路电流的一种特殊情况,因此不难看出网孔电流的个数为b-(n-1)。 支路电流法,网孔电流法,节点电压法,为一般的电路分析方法,在我们对一个电路进行方程选取过程中,通过对电路的观察尽可能多的获得已知量,从而简化方程复杂度,以下为一些常用的方程选取的一般性原则: 1、支路为独立电流源/电压源可以直接确定该条支路的电流/电压结果 2、选取合适的0电压参考点可以大大简化方程的复杂度 3、对于“平面电路”可以直接利用网孔电流法,而无需找“树”和“枝干” 当然,最最重要的是灵活应用基尔霍夫定律!!通过在电路图上局部列写基尔霍夫方程尽可能多的确定电路参数,对于不是太过复杂电路可以很快得出结果,但是因为由于没有进行独立方程的区分,可能会列出非独立的方程,使得局部电路方程无解,这样需要寻找更多非关联的信息来求取电路方程。 2、电路的矩阵形式 学过《线性代数》的我们知道,方程组的形式可以等效为矩阵的形式,将系数矩阵


![积分电路的波形图_微分电路波形插图37 Z=[Y]^{-1}](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
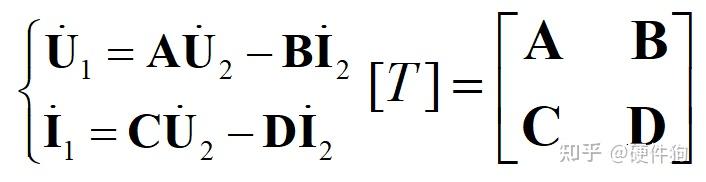
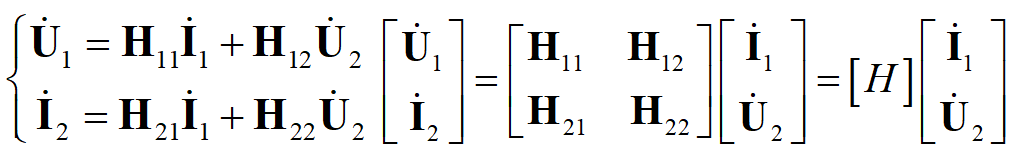

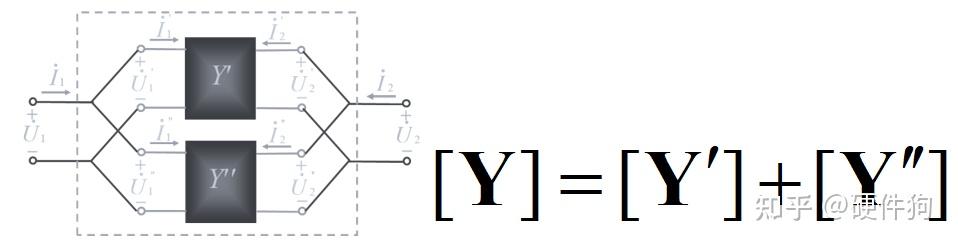
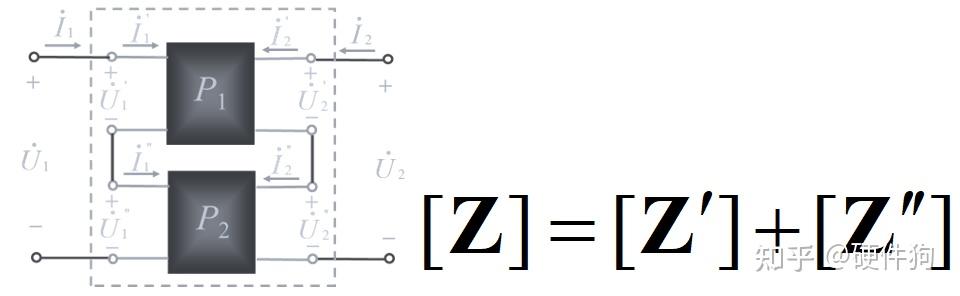
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/22074.html