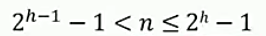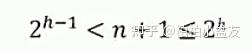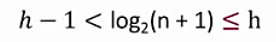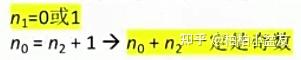树和二叉树的定义及性质
一、树
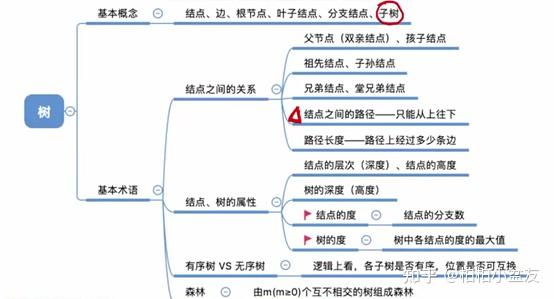
（1）树是什么
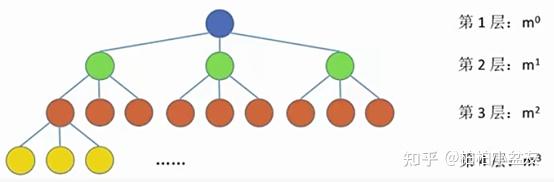
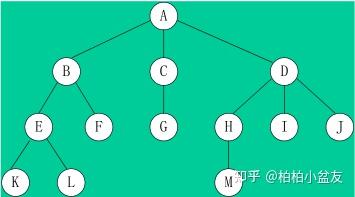
请看图：
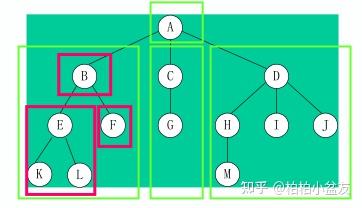
树（Tree）是n（n>=0）个结点的有限集，它或为空树（n=0）；对于非空树：有且仅有一个称之为根的结点；除根结点以外的其余结点可分为m（m>0）个互不相交的有限集T1，T2，…，Tm，其中每一个集合本身又是一棵树，并且称为根的子树（SubTree）。
它的逻辑关系是一对多的关系，并且体现一种明显的递归特性，也就是当前每一层（每一个子结构）和上一层（父结构）有着相似的分支结构，
（2）树的基本术语
结点：树中的一个独立单元。包含一个数据元素及若干指向其子树的分支，如上图中的A、B、C、D等。结点的度：结点拥有的子树数。例如，A的度为3，C的度为1，F的度为0。树的度：树的度是树内各结点度的最大值。上图中所示的树的度为3叶子：度为0的结点称为叶子或终端结点。结点K、L、F，G、M、1、J都是树的叶子。非终端结点：度不为0的结点称为非终端结点或分支结点。除根结点之外，非终端结点也称为内部结点。双亲和孩子：结点的子树的根称为该结点的孩子，相应地，该结点称为孩子的双亲。例如，B的双亲为A，B的孩子有E和F。兄弟：同一个双亲的孩子之间互称兄弟。例如，H、1和J互为兄弟。堂兄弟：双亲在同一层的结点。例如，结点G与E，F，H.1.J互为堂兄弟。祖先：从根到该结点所经分支上的所有结点。例如，M的祖先为A、D和H.子孙：以某结点为根的子树中的任一结点都称为该结点的子孙。如B的子孙为E、K、L和F。层次：结点的层次从根开始定义起，根为第一层，根的孩子为第二层。树中任一结点的层次等于其双亲结点的层次加1。树的深度：树中结点的最大层次称为树的深度或高度。图中所示的树的深度为4有序树和无序树：如果将树中结点的各子树看成从左至右是有次序的（即不能互换），则称该树为有序树，否则称为无序树。在有序树中最左边的子树的根称为第一个孩子，最右边的称为最后一个孩子。森林：是m（m20）棵互不相交的树的集合。对树中每个结点而言，其子树的集合即为森林。由此，也可以用森林和树相互递归的定义来描述树。
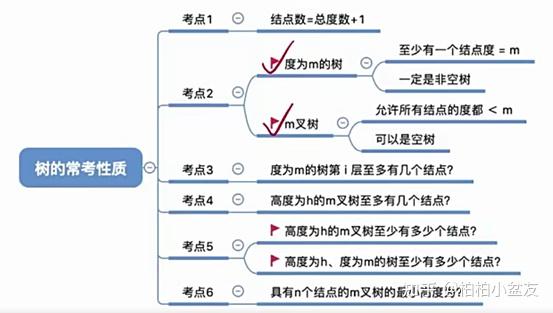
2、树的性质
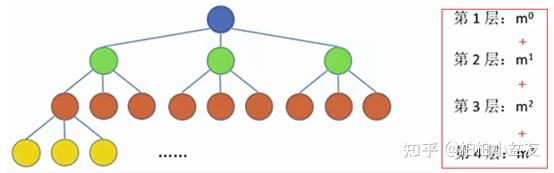
（1）结点数=总度数+1结点：树中的一个独立单元结点的度：结点拥有的子树数，也就是那一根线。+1是因为根节点没有前驱也就没有线了
（2）度为m树、m叉树的区别（选择题考点）
（3）度为m的树或m叉树，第i层至多有m^(i-1)个结点（i>=1）
（4）高度为h的m叉树至多有m^h-1/m-1个结点
（5）高度为h的m叉树至少有h个结点；
高度为h，度为m的树至少有h+m-1个结点（在中必须有一结点的度为m）；
（6）有n的结点的m叉树的最小高度为
二、二叉树
1、二叉树是什么
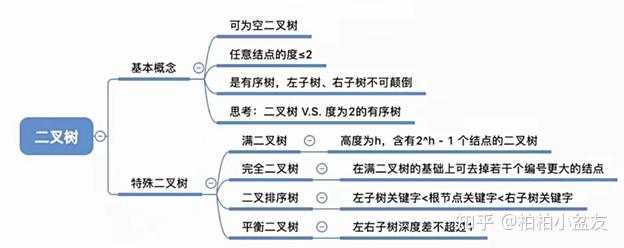
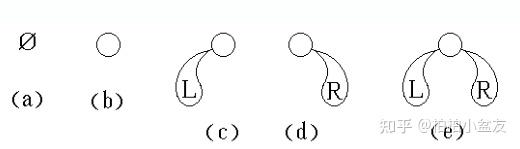
二叉树（Binary Tree）是n（n>0）个结点所构成的集合，它或为空树（n=0）；或为非空树，对于非空树。有且仅有一个称之为根的结点；除根结点以外的其余结点分为两个互不相交的子集T1和T2，分别称为T的左子树和右子树，且T和工本身又都是二叉树。
二叉树特点：·结点的度小于等于2·有序树（子树有序，不能颠倒）根据定义，有五种基本形态：
2、特殊的二叉树
（1）满二叉树：除了叶子结点以外，所有分支结点的度数都是2
结点数=2^高度-1
特点：只有最后一层有叶子结点不存在度数为1的结点按层序从1开始编号，结点n的左孩子编号为2n，右孩子编号为2n+1，父结点编号为n/2。
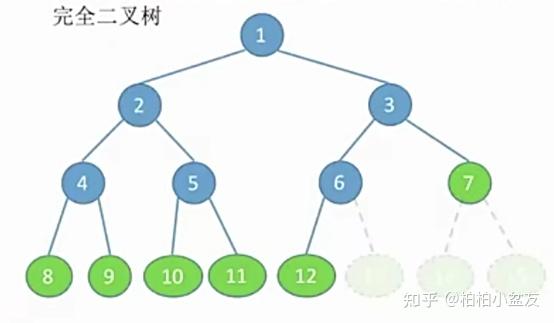
（2）完全二叉树：少了些叶子结点时，具有的编号都能和满二叉树一一对应上。
特点：只有最后两层可能有叶子结点，最多只有一个度为1的结点按层序从1开始编号，结点n的左孩子编号为2n，右孩子编号为2n+1，父结点编号为n/2（如果存在）当有i个结点，结点编号为n，n<=(i/2)时为分支结点，n>(i/2)时为分支结点
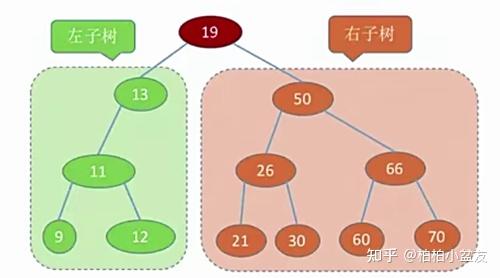
（3）二叉排序树（想一想二分法）左子树所有的关键字小于根结点的关键字右子树所有的关键字大于根节点的关键字左子树和右子树又各是一个二叉排序树
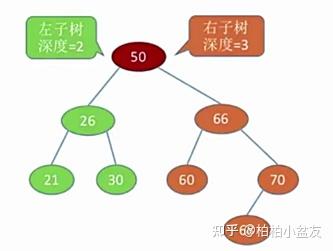
（3）平衡二叉树：任何一结点的左子树和右子树的深度之差不超过1.
3、二叉树的性质
考点1：设非空二叉树中度为0、1和2的结点个数分别为n0，n1和n2，则n0=n2+1（叶子结点比二分支结点多一个）（选择题）
设结点数为n，则有：①n=n0+n1+n2结点数=度为0的结点数+度为1的结点数+度为2的结点数②n=n1+2n2+1结点数=度为1的结点数*延伸出来的度数1+度数为2的结点数*延伸出来的度数2+根结点1③结点数=总度数+1②-①得：n0=n2+1
考点2：二叉树第i层至多有2^(i-1)个结点（i>=1）
m叉树第i层至多有m^(i-1)个结点（i>=1）
考点3：高度为h的二叉树至多有2^h-1个结点（满二叉树）
高度为h的m叉树至多有 m^h一1/m-1个结点
考点4：具有n个结点（n>0）的完全二叉树的高度计算：
得：
两边对数得第一个式子：
第二个式子：
同理得：
所以知道：
考点5：对于完全二叉树，可以由的结点数n推出度为0、1和2的结点个数为n0，n1和n2
根据完全二叉树最多只有一个度为1的结点，即
得
以上就是树和二叉树的定义和性质，希望对你有所帮助
感谢浏览，祝你学习快乐！
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/94575.html
