【王道408数据结构习题整理】7.2 顺序查找和折半查找 理论
前言
王道408数据结构习题目录
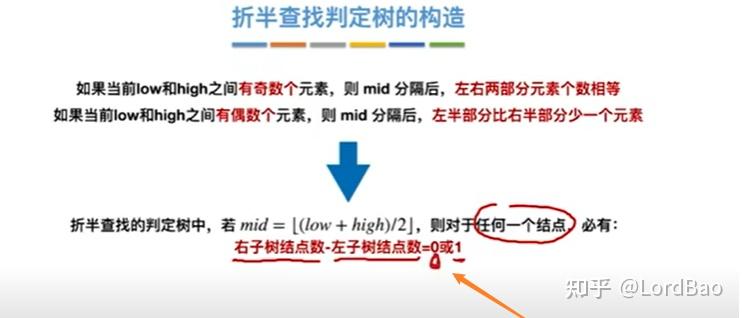
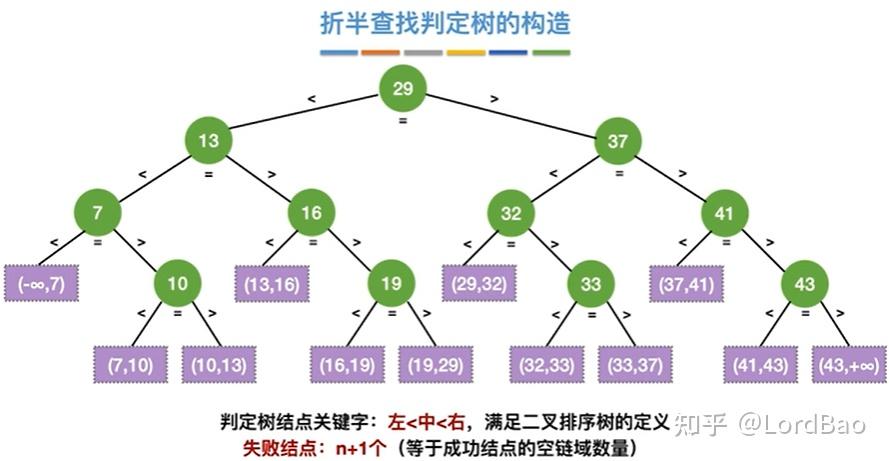
折半查找
结论1
结论2
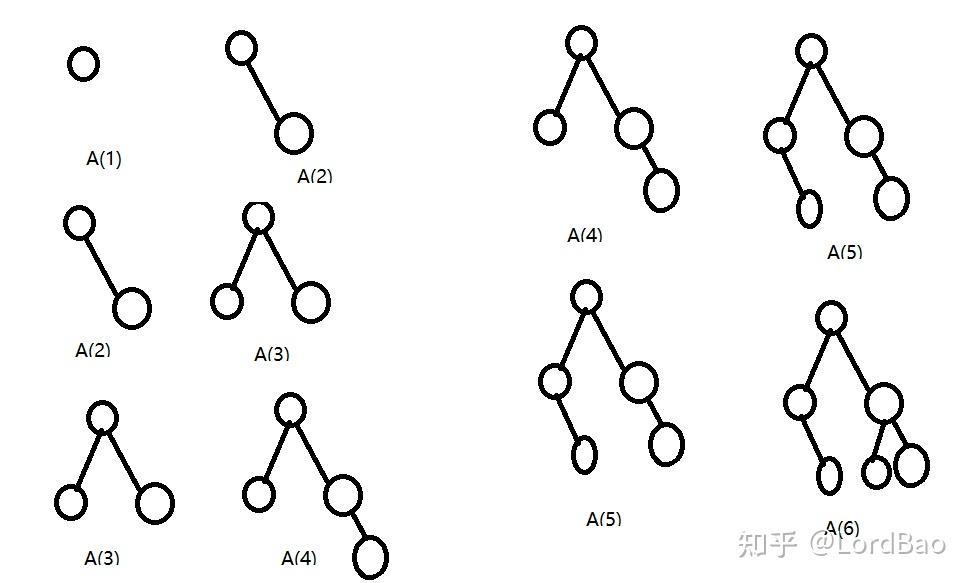
复习:假定存在一棵树



折半查找的判定树一定是平衡二叉树。但与前面一个结论:右子树的节点 减去 左子树的节点为0或1 有出入,请与平衡二叉树的定义区分。
粗糙地说明为什么折半查找的判定树一定是平衡二叉树。注意,直观上看判定树的生成过程可以看出它是平衡二叉树。
结论1:假定树的节点为n,则对于每个n,都有唯一判定树形式。
证明:
当
当





至此,我们说明了
考虑一棵




由此可知,若保证

考虑集合










可以推出,对于每个整数


因此,对于任意的

证毕!
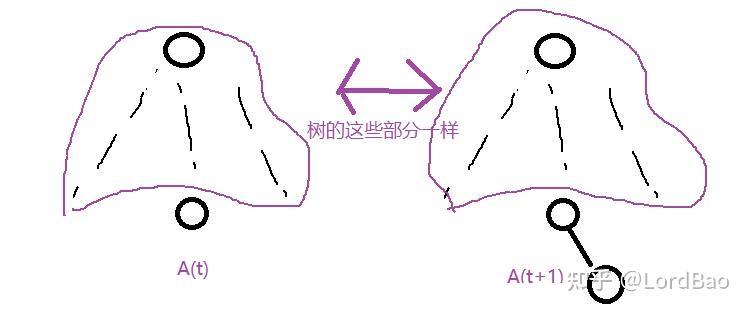
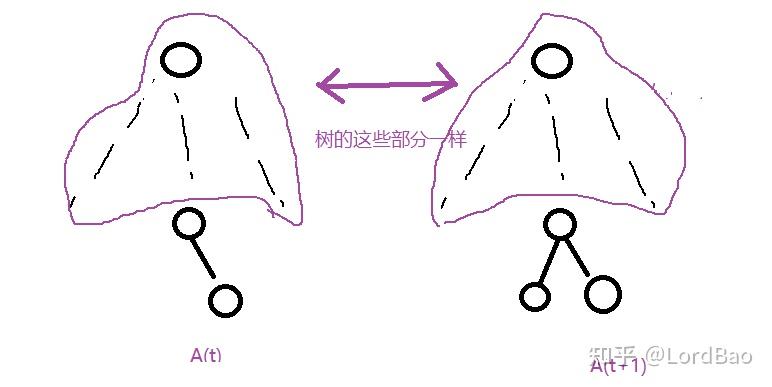
观察1 :令



若










若










总之,





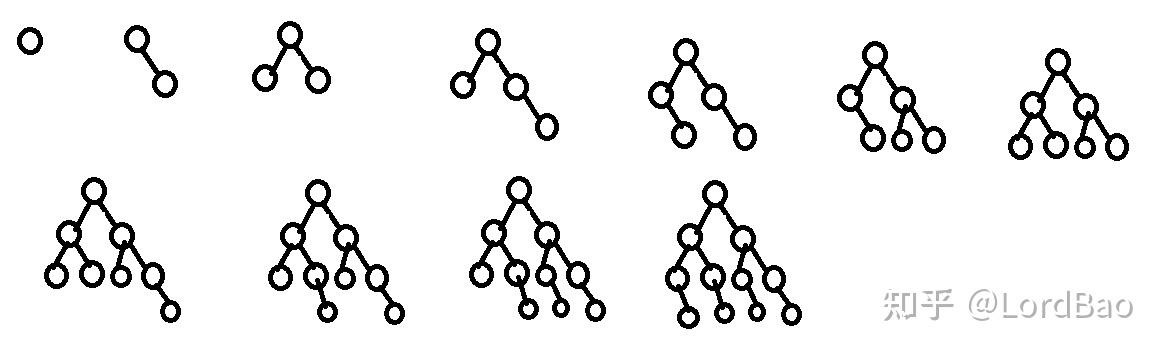
我们可以列举
对于任意大于5的整数




也就是说,














综上所述,





结论2:折半查找的判定树一定是平衡二叉树。
证明:
假定判定树有n个结点,考虑以树上任意节点为根节点的子树
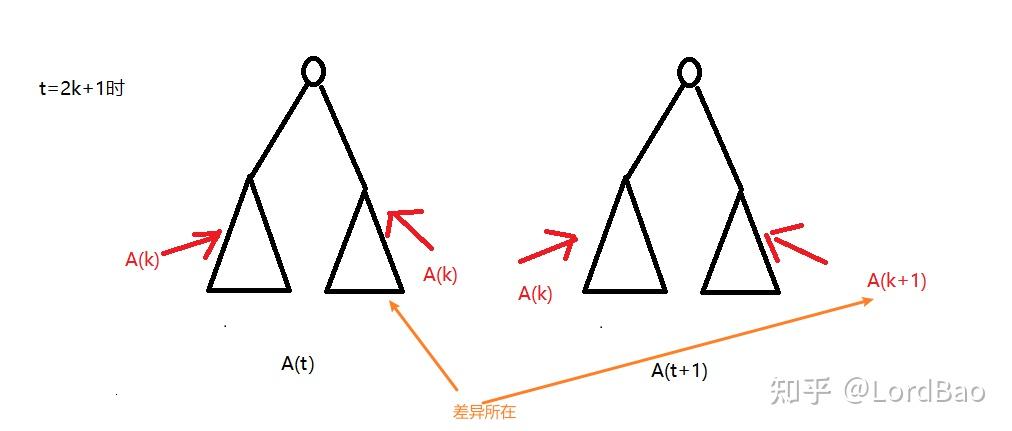
若

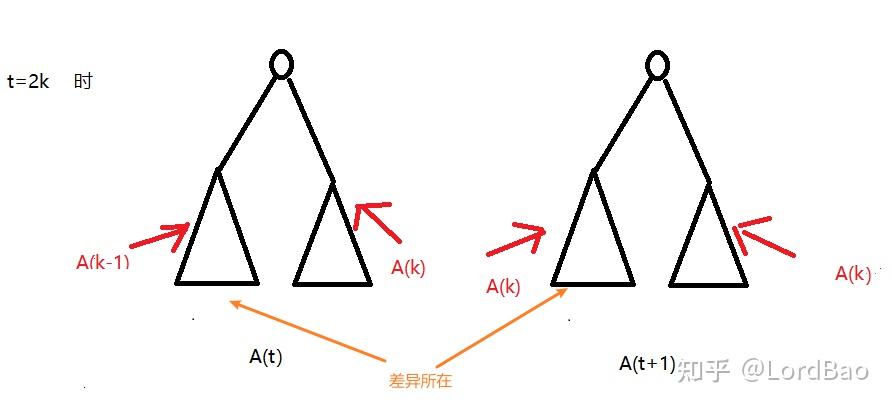
若
1、

2、

由于
证毕!
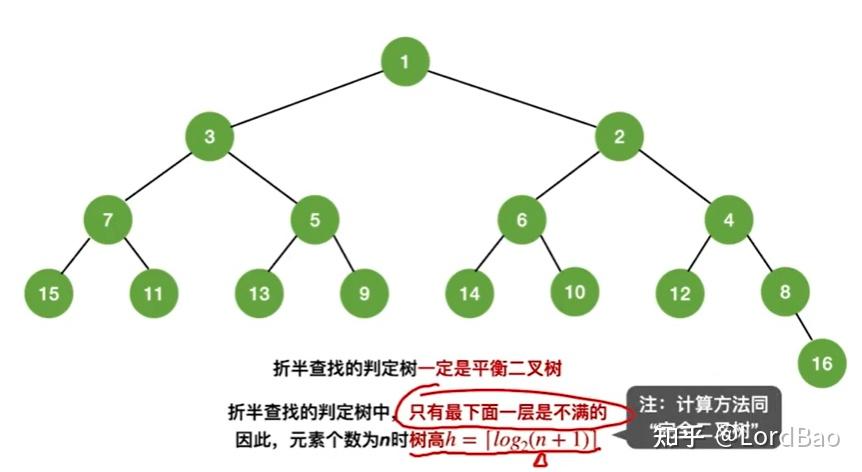
结论3:折半查找的判定树只有最下面一层不满,即假定判定树高为h,则它的前h-1层必然是满二叉树。假定判定树的节点个数为

证明:
从构造判定树的过程来看,折半查找的判定树只有最下面一层不满,即假定判定树高为h,则它的前h-1层必然是满二叉树这一点是成立的。
怎么证明这一点,我说不清楚,感觉从判定树的构成过程就体现了这一点。
折半查找的判定树只有最下面一层不满,且折半查找的判定树实际上是同等高度的满二叉树的子图。因此,假定判定树的高度为h,则
故而
证毕!
结论3
最后的折半查找判定树是二叉排序树,失败节点为n+1个。
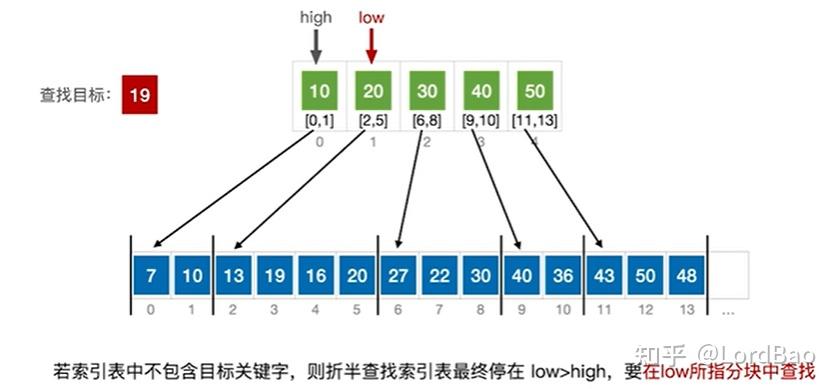
分块查找
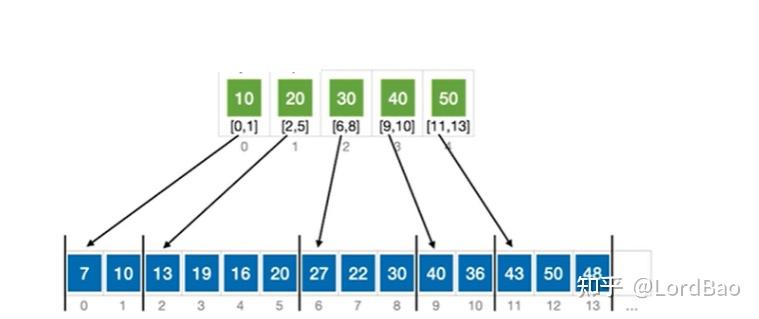
分块查找的基本思想
注意索引表上的顺序查找和折半查找和我们常规说的不一样。
索引表上进行顺序查找:
判断key是否小于等于第一个块的索引值,若为true,转为第一个块查找,若为false,判断key是否小于等于第二个块的索引值,若为true,则转为第二个块查找,以此类推。失败的情况有2种,1、key大于索引表的所有关键字;2、某个块中没有key对应的元素。
索引表上进行折半查找:
注意,我跟王道上的做法不一样。。。
观察:
1、上面的索引表关键字10,20,30,40,50实际上划分了 6个区间![折半查找判定树和二叉排序树的区别_折半查找判定树是二叉排序树吗插图149 A_1=(-\infty,10],A_2=(10,20],A_3=(20,30],A_4=(30,40],A_5=(40,50],A_6=(50,+\infty)](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
其中
2、代码框架
1、在处理key 在
2、while循环中的内部中,有一行代码,至于为什么这么做,原因写在代码里面了。
3、怎么处理while中的条件?这个是最重要的一环。
我们进行一些观察:
1、当

也就是说当


2、当

也就是说当

综上可知,初始区间为



我们断言,对于任意的整数










因此,在执行上述循环体代码时,要么key匹配,要么最后搜索的区间长度为2或3。
当搜索区间长度为2时,
若key不匹配,则最终区间长度为1。
当搜索区间长度为3时,
若key不匹配,则最终区间长度为1或2,对于2的情况,其最终仍然变为区间长度为1的情况。
总之,若key不匹配,最终的结果是搜索区间长度变为1,即的情况,由于我们所在的key仅可能在下标 [low,high] 所在分块中,因此我们只需要对此时的low(或high)所在分块进行查询即可。
因此循环的判断应该写为。
完整的代码如下
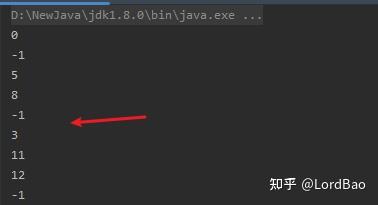
针对此表,设计测试案例 7,8 20,30 12,19 43,50,51
测试代码
测试结果
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/92666.html