随处可见的红黑树详解
前言
刚开始接触红黑树的时候,感觉很难。其实不然,红黑树只是情况分的多了一点而已,相较于线段树,主席树等等,简单多了。对于红黑树3种插入维护4种删除维护没必要去记忆,稍作了解,对于红黑树的性质和特点,需要特别记忆。
注意,本文图中红黑树的叶子结点默认不画出来
为什么要有红黑树
二叉搜索树
二叉搜索树(又叫二叉排序树,BST):对于任意一个结点,其左子树的值必定小于该结点,其右子树的值必定大于该结点。那么中序遍历的时候,就是有序的了。理论上来说,增加,删除,修改的时间复杂度都是O(log(N))。但是它存在一个致命的问题。
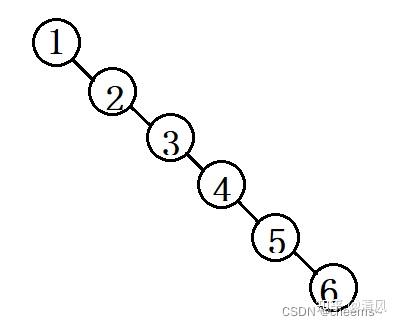
退化:向树中插入[1,2,3,4,5,6],此时树退化成了一个链表,增加,删除,修改的时间复杂度退化为O(N)
平衡二叉搜索树
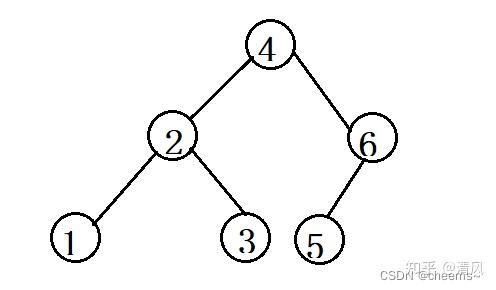
平衡二叉搜索树(AVL Tree):它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉搜索树。如果向树中插入[1,2,3,4,5,6]
可以看到AVLTree在最坏的情况下,依然保持了“绝对的平衡”:左右两个子树的高度差的绝对值不超过1。那么AVL Tree是如何保证平衡的呢,是通过旋转,可以看到,无论是插入还是删除元素,都要去通过旋转维护整个树的平衡。 AVL查询元素:O(log(N)) AVL插入元素:最多一次旋转O(1),加上查询的时间O(log(N)),插入的复杂度O(log(N)) AVL删除元素:必须检查从删除结点开始到根结点路径上的所有结点的平衡因子。因此删除的代价比较大,删除最多需要log(N)次旋转,加上查询的时间,删除的复杂度O(2log(N))
红黑树
我们发现,AVL树未免太严格了一些,有没有一种数据结构,能让AVL树不那么严格平衡,降低维护平衡的开销,同时又不能像BST一样退化呢?
当然有,就是本文所写的红黑树(rbTree): rbTree查询元素:O(log(N)) rbTree插入元素:插入最多2次旋转,加上查询的时间O(log(N)),插入的复杂度O(log(N)) rbTree删除元素:删除最多需要3次旋转,加上查询的时间,删除的复杂度O(log(N))
虽然插入和删除元素后,需要旋转和变色(本文中统一为维护),但是这一时间复杂度可以估算为O(1)不计
因为rbTree的第6条性质(见下文) – ==所以红黑树的查询效率略低与AVL的查询== – ==红黑树和AVL插入的速度差不多== – ==红黑树删除的速度比AVL快,因为AVL删除最多需要og(N)次旋转==
红黑树的应用场景
c++ stl map,set(红黑树的封装)进程调度cfs(用红黑树存储进程的集合,把调度的时间作为key,那么树的左下角时间就是最小的)内存管理(每次使用malloc的时候都会分配一块小内存出来,那么这么块就是用红黑树来存,如何表述一段内存块呢,用开始地址+长度来表示,所以key->开始地址,val->大小)epoll中使用红黑树管理socketfdnginx中使用红黑树管理定时器,中序遍历第一个就是最小的定时器
红黑树的性质(重点)
==1. 每个结点是红的或者黑的 2. 根结点是黑的 3. 每个叶子结点是黑的(因为这条性质,一般用叶子结点在代码中被特殊表示) 4. 如果一个结点是红的,则它的两个儿子都是黑的(不存在相邻红色) 5. 从任一节点到叶子节点,所包含的黑色节点数目相同(即黑高度相同) 6. 最长路径长度不超过最短路径长度的2倍(2n-1,一条黑红黑红….一条全黑)==
红黑树的定义
红黑树的左旋与右旋
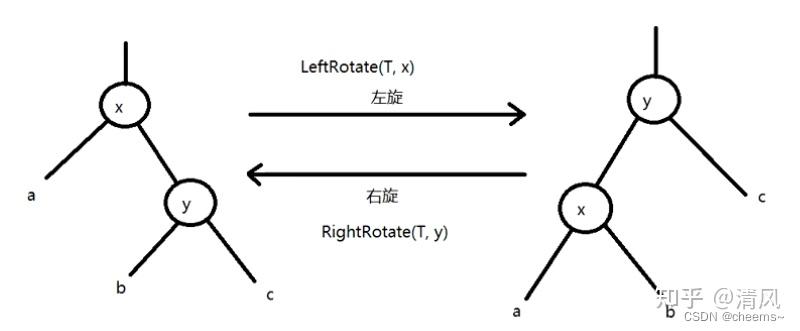
动三个方向,改6个指针。 通过旋转,调整左右高度,使树达到平衡。
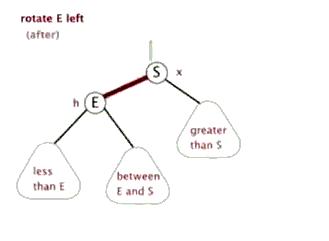
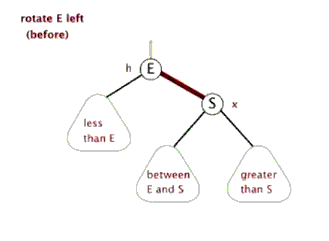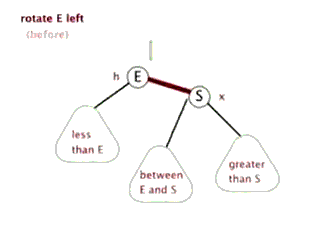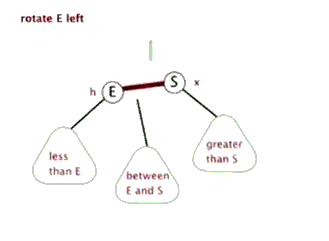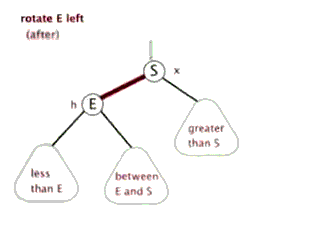
左旋leftRotate(T,x)—中右->左中
降低X结点的高度,提高X结点右结点(即Y)的高度。x的右子树指向y的左子树本来指向x结点的父指针,改成指向yy的左子树指向x结点
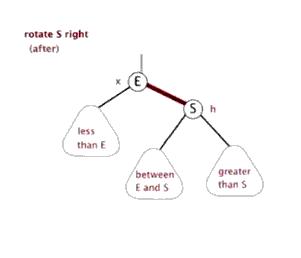
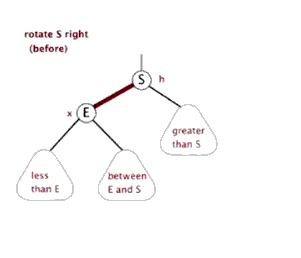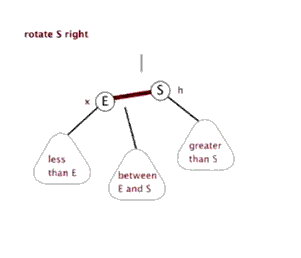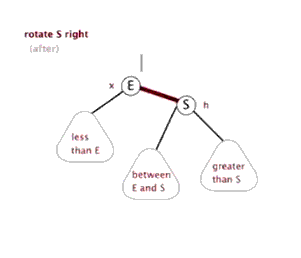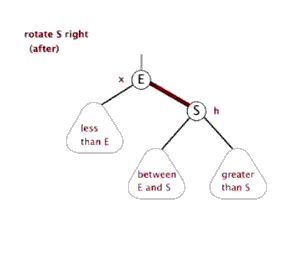
右旋rightRotate(T,y)—中左->中右
降低Y结点的高度,提高Y结点左结点(即X)的高度。y的左子树指向x的右子树本来指向y结点的父指针,改成指向xx的右子树指向y结点
红黑树插入结点与插入维护红黑树的三种情况
插入结点
在插入结点时,我们始终认为“==插入这个结点之前,原来的红黑树是满足红黑树性质的====”,那么插入的位置容易找,就是不断的对比key,最终找到位置,那么新增的结点是什么颜色呢?我们通过性质发现: – 如果新结点是黑色,违背了第5条性质 – 如果新结点是红色,可能违背第4条性质
而第四条性质,我们可以通过旋转与上色的方式修复,所以在我们插入结点的时候,我们始终认为新结点是红色
插入结点后维护红黑树
我们知道新增结点是红色,如果新结点是父节点也是红色,那么就需要维护红黑树了。
如果父结点是爷结点是左子树,可以归纳出来三种情况。同理如果父结点是爷结点是右子树,我们也可以归纳出来三种情况。但是这三种情况的差异就是旋转方向的区别而已。一共是6种情况,但是归纳出来其实是3种,读者不要搞错了。
在下面的图中:z表示新增结点,y表示叔结点
父结点是爷结点是左子树
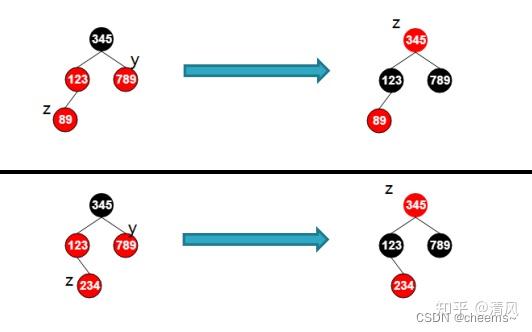
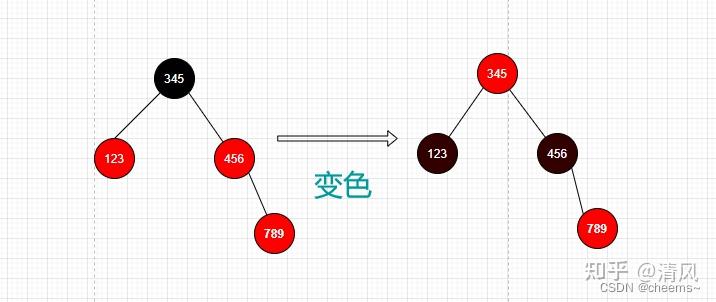
1. 叔结点是红色的
将叔结点和父结点变黑,爷结点变红将当前结点变成爷结点(因为爷结点是红,爷结点的父节点也可能是红,所以要递归维护)
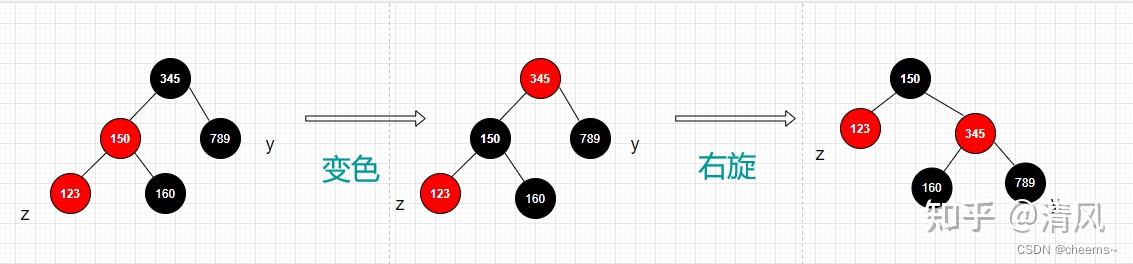
2. 叔结点是黑色的且新结点是左子树
将父结点变成黑色,爷结点变成红色以爷结点为中心右旋
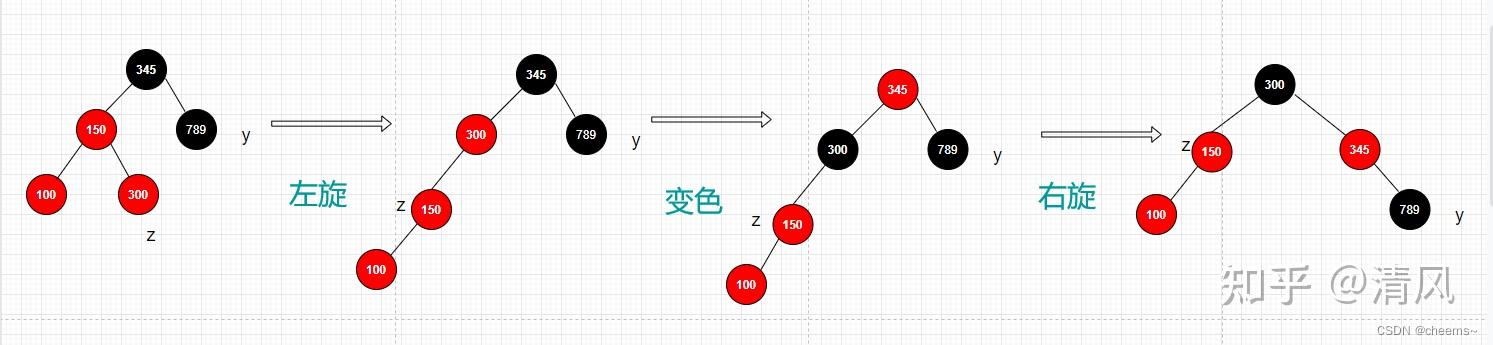
3. 叔结点是黑色的且新结点是右子树
以父结点为中心左旋将父结点变黑色,爷结点变红色以爷结点为中心右旋
父结点是爷结点是右子树
1. 叔结点是红色的
将叔结点和父结点变黑,爷结点变红将当前结点变成爷结点(因为爷结点是红,爷结点的父节点也可能是红,所以要递归维护)
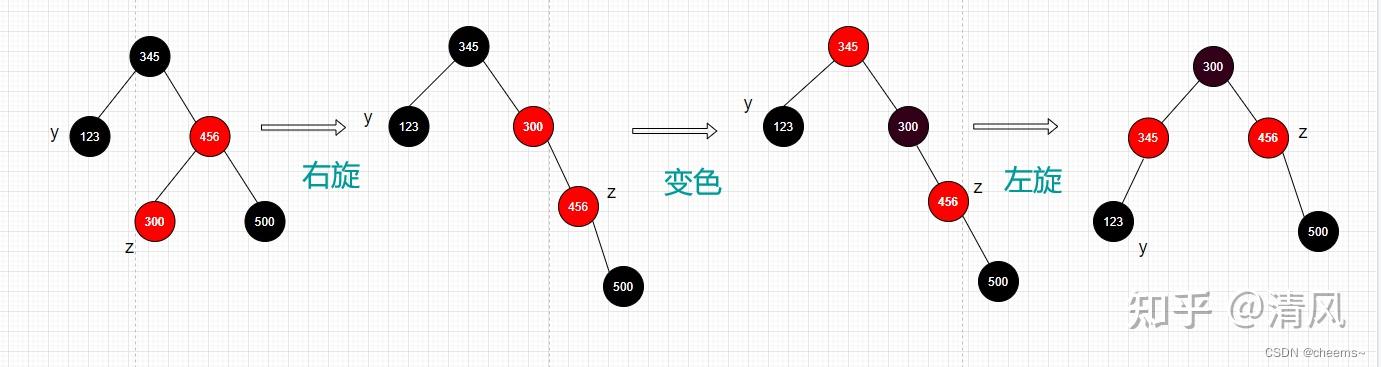
2. 叔结点是黑色的且新结点是左子树
以父结点为中心右旋将父结点变黑色,爷结点变红色以爷结点为中心左旋
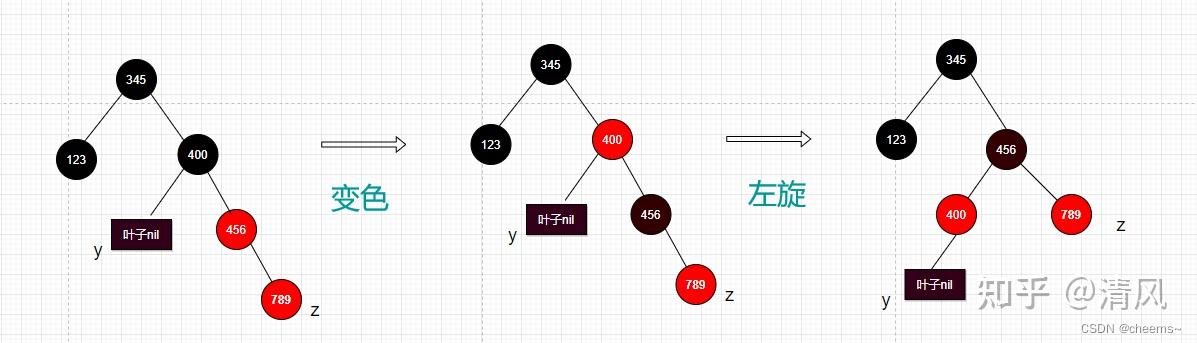
3. 叔结点是黑色的且新结点是右子树
将父结点变成黑色,爷结点变成红色以爷结点为中心左旋
维护代码
红黑树删除结点与删除维护红黑树的四种情况
删除结点
我们定义:覆盖结点:z(被指定删除的结点,实际上被覆盖)删除结点:y(实际上被删除的结点,一般是后继结点)轴心结点:x(维护红黑树的结点)
红黑树删除结点根据改结点的左右子树分为三种情况:没有左右子树有且仅有一个子树左右子树都有
对不同情况的处理: – 情况1:直接删除该结点 – 情况2:将该结点的唯一子树挂到父结点上,然后删除该结点 – 情况3:找一个删除结点y(后继结点)覆盖 指定结点z,然后删除 删除结点y,对于这个删除结点y来说,它的情况一定是情况1或情况2
删除代码
删除结点后维护红黑树
想一想,删除一个结点,该结点是什么颜色的时候才需要维护红黑树呢? – 如果是红色,没有违反任何性质。所以如果是红色直接删除即可,无需维护 – 如果是黑色,黑色被删除,那么必定违反第5条性质,破坏了黑高,所以我们需要针对这一情况进行维护
如果当前结点是父结点的左子树的情况,可以归纳出来四种情况。同理如果当前结点是父结点的右子树,我们也可以归纳出来四种情况。但是这四种情况的差异就是旋转方向的区别而已(镜像的)。一共是8种情况,但是归纳出来其实是4种,读者不要搞错了。
当前结点是父结点的左子树的情况
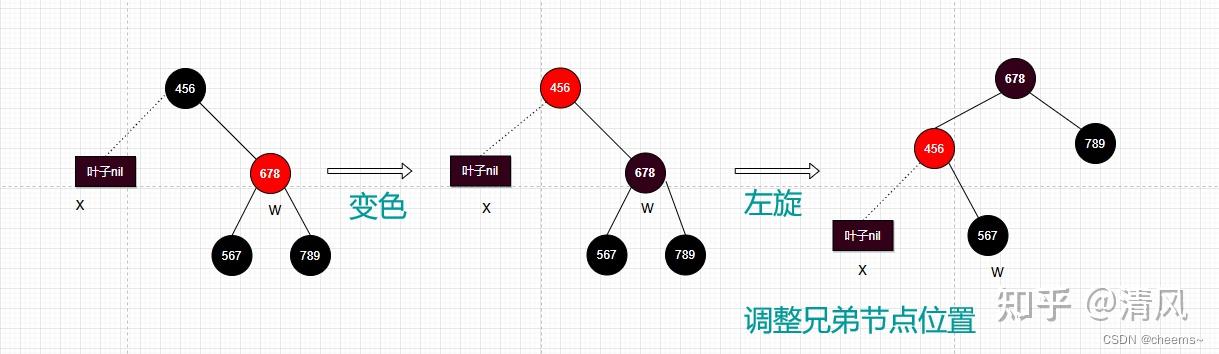
1. 当前结点的兄弟结点是红色的
兄弟节点变成黑色父节点变成红色父节点做左旋将兄弟结点调整为父节点的右子树
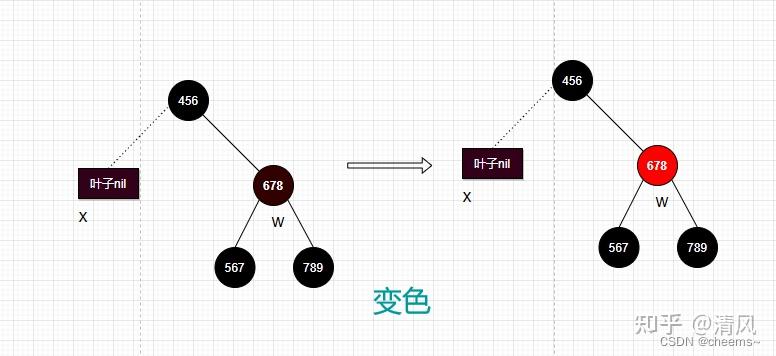
2. 当前结点的兄弟结点是黑色的,而且兄弟结点的两个孩子结点都是黑色的
兄弟节点变成红色轴心结点变为父节点
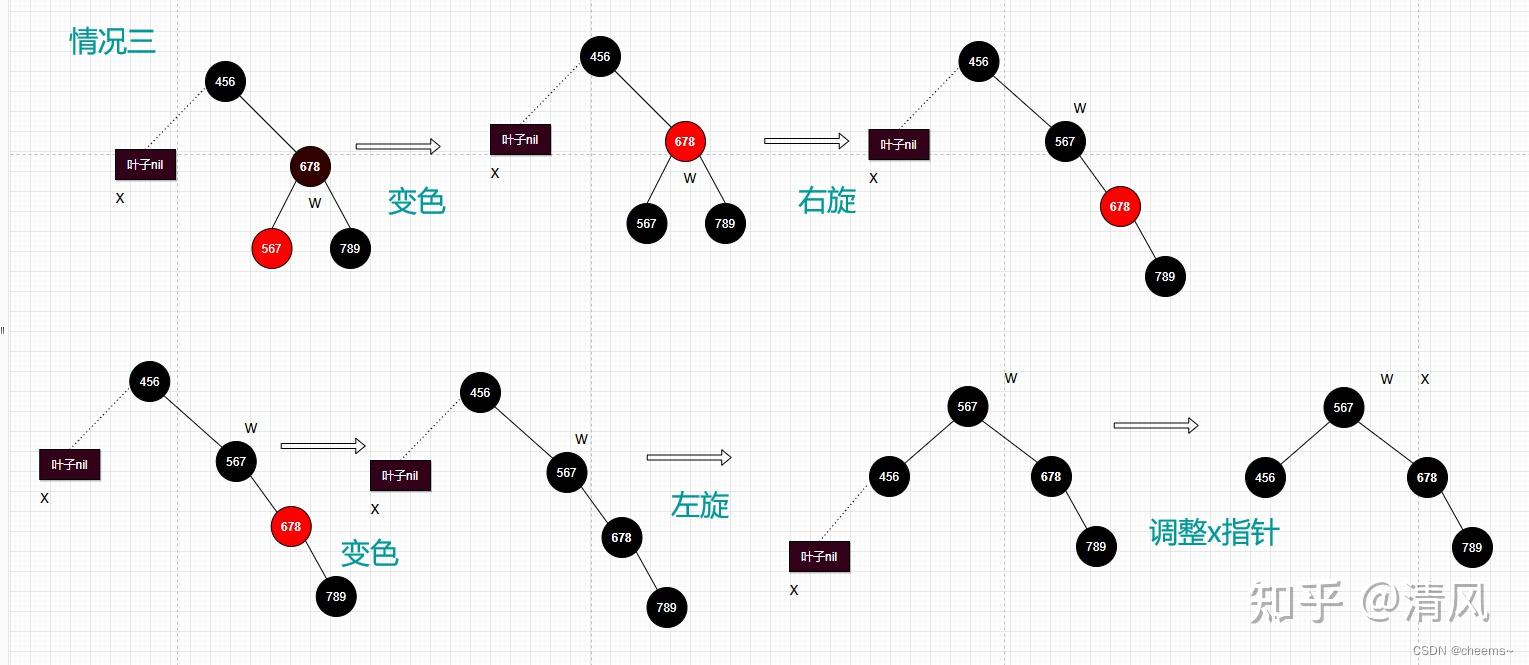
3. 当前结点的兄弟结点是黑色的,而且兄弟结点的左孩子是红色的,右孩子是黑色的
将左孩子涂黑将兄弟节点变红对兄弟节点右旋 将兄弟结点调整为父节点的右子树 现在情况3就会变成情况4,接着做情况4的步骤
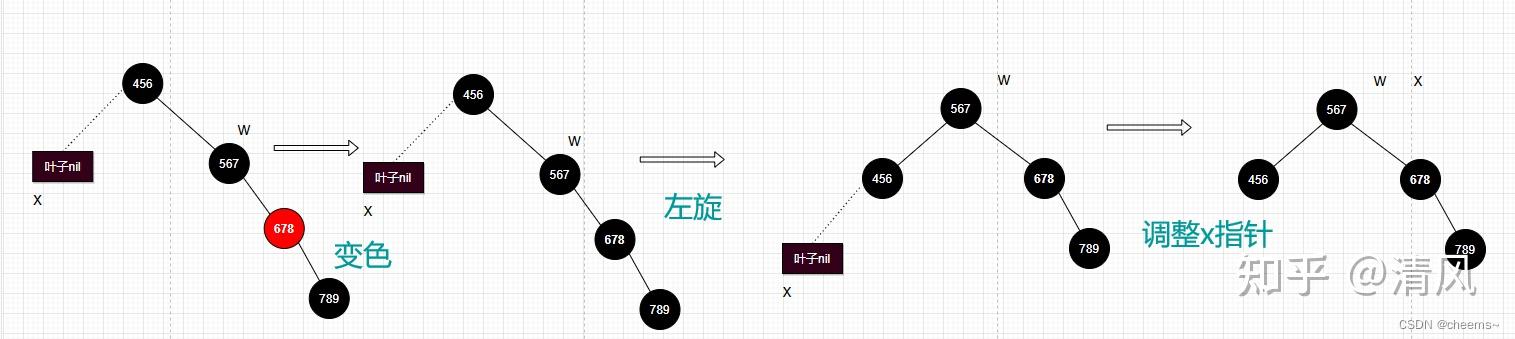
4. 当前结点的兄弟结点是黑色的,而且兄弟结点的左孩子是黑色的,右孩子是红色的
将兄弟节点换成父节点的颜色把父节点和兄弟节点的右孩子涂黑对父节点做左旋设置x指针,指向根节点
当前结点是父结点的右子树的情况
1. 当前结点的兄弟结点是红色的
兄弟节点变成黑色 父节点变成红色 父节点做右旋 将兄弟结点调整为父节点的左子树
2. 当前结点的兄弟结点是黑色的,而且兄弟结点的两个孩子结点都是黑色的
兄弟节点变成红色 轴心结点变为父节点
3. 当前结点的兄弟结点是黑色的,而且兄弟结点的左孩子是黑色的,右孩子是红色的
将右孩子变黑 将兄弟节点变红 对兄弟结点左旋 将兄弟结点调整为父节点的左子树 现在情况3就会变成情况4,接着做情况4的步骤
4. 当前结点的兄弟结点是黑色的,而且兄弟结点的左孩子是红色的,右孩子是黑色的
将兄弟节点换成父节点的颜色 把父节点和兄弟节点的左孩子变黑 对父节点做右旋 将轴心结点调整为根结点
维护代码
红黑树的遍历、查询、测试
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/92383.html