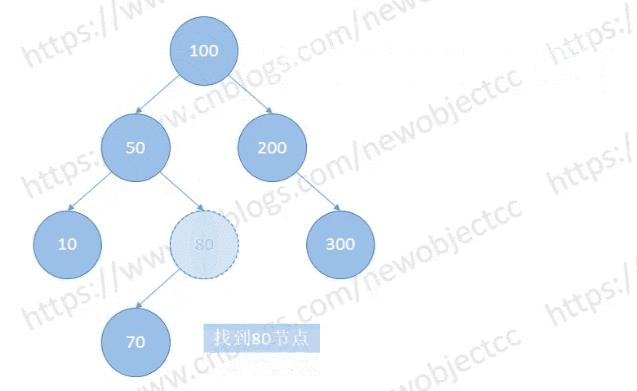
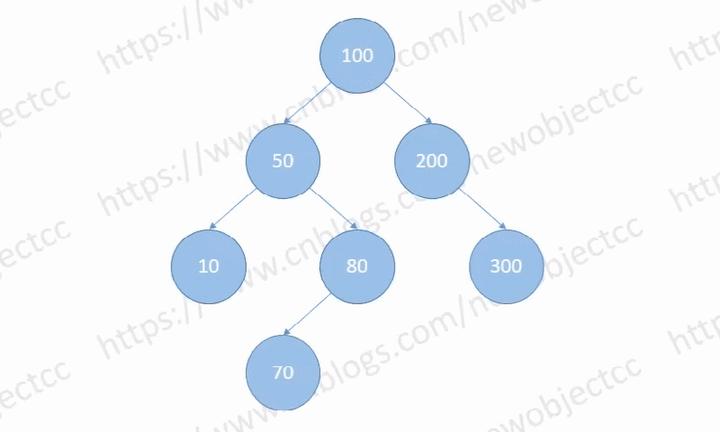
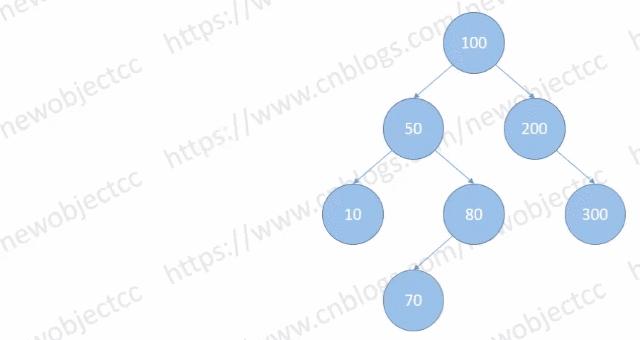
红黑树与普通的平衡二叉树除了颜色到底有什么区别？为什么要引入红黑树，它比普通的平衡二叉树究竟好在哪？ 类似问题：红黑树比 AVL 树具体更高效在哪里？ 大家好，我是阿呆【Coder阿呆】，一个不务正业的程序员。 要想知道这二者的区别，就要从根本上理解这二者的原理是什么，以为内容比较多，这里先说下二叉搜索树的原理以及红黑树旋转内容。 只讲原理，不谈具体实现，最多只是伪代码。内容有点长，也有点干，建议看完。（本文部分原理图来自：CSDN-NO编程 ) 0、二叉查找树 二叉查找树（Binary Search Tree），也称有序二叉树（ordered binary tree），排序二叉树（sorted binary tree），是指一棵空树或者具有下列性质的二叉树：若任意结点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；若任意结点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；任意结点的左、右子树也分别为二叉查找树。没有键值相等的结点（no duplicate nodes）。 下图是一棵典型的二叉查找树：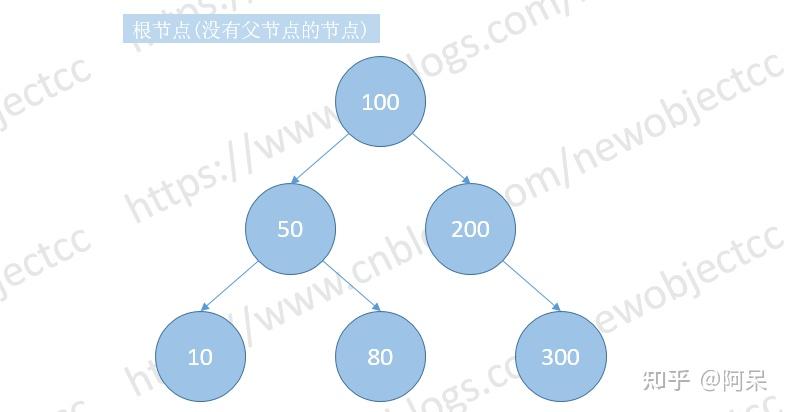 
对于一棵二叉树来说，最重要的就是它的结点插入、删除和查找，下面我们分别来看一下，对于二叉查找树，是如何完成这些动作的。 0.1、插入结点 插入结点就是从根结点开始查找比较，如果要插入的结点值大于比较的结点，就取比较结点的右子节点比较，否则就取左子节点比较，直到比较结点为叶子结点，然后根据值的大小，插入到叶子结点的左侧或者右侧。来看一张动图理解一下。 依次插入结点[100,50,200,80,300,10] 
看图是不是很好理解，我们再来看下对应的伪代码： 0.2、查找结点 查找结点其实在刚才的插入结点中就有所体现了，其实就是那一段while循环，这里就不再放伪代码了，直接看个动图。 
0.3、删除结点 二叉查找树的删除结点，就是先找到要删除的结点，然后从树中移除。 但是删除的时候会出现一些复杂的情况，我们来总结一下：1、要删除的结点没有子结点，代表要删除一个叶子结点，这是最简单的情况，直接移除就好2、要删除的结点有一个子结点，3、要删除的结点有两个子结点， 我们先来看最简单的情况，也就是要删除的结点是叶子结点的时候，还是来看一张动图。这张图里我们要删除的结点是70。 
我们再来看另外一种情况，要删除的结点有一个子结点的情况。这种情况下，只需要把要删除的结点的子结点，交给它的祖父节点，也就是要删除结点的父节点，然后再删除就好了。 下面这张图我们要删除的结点是200。 
最后来看一下最复杂的情况，删除有两个子结点的结点，这种情况要涉及到结点的位置变换，需要用该结点的右子树中最小结点替换当前节点。我们通过动图来理解一下。比如我们要删除的是50结点。 
最后我们来看下上边这三种情况的伪代码。 0.3、二叉查找树的缺点 由于二叉查找树是一种非平衡树，由于插入数据的顺序，可能会导致所有的结点都倾向于一侧，这种极限情况下，树就变成了一个线性结构，相当于链表。 这种不平衡会导致树的层级增多，也就是高度增加，从而导致查找和插入的效率变低。时间复杂度从O(log n)变为O(n)。 那么如何避免这个问题呢，只需要在每次插入或者删除结点的时候，去动态的维持树的平衡，就不会出现数据向某一侧倾倒的情况了。 而红黑树正是通过这样的方式，来动态保证树的平衡。接下来我们正式介绍红黑树。 1、红黑树 前面我们已经说过，红黑树，本质上来说就是一棵二叉查找树，但它在二叉查找树的基础上增加了着色和相关的性质，使得红黑树相对平衡，从而保证了红黑树的查找、插入、删除的时间复杂度最坏为O(log n)。 但它是如何保证一棵n个结点的红黑树的高度始终保持在h = logn的呢？这就引出了红黑树的5条性质：1）每个结点要么是红的，要么是黑的。2）根结点一定是是黑的。3）所有叶子结点（叶子结点即指树尾端NIL指针或NULL结点）一定是黑的。4）如果一个结点是红的，那么它的俩个子结点一定都是黑的。5）从任一结点出发，到叶子结点的每一条路径，都包含相同数目的黑结点。 正是红黑树的这5条性质，使得一棵n个结点是红黑树始终保持了logn的高度，从而也就解释了上面我们所说的 “红黑树的查找、插入、删除的时间复杂度最坏为O(log n)” 这一结论。 我们先来看一下一棵标准的红黑树是什么样子： 
上面我们所说的 “叶子结点” 或”NIL结点”，它不包含数据而只充当路径在此结束的一个指示，这些结点在绘图中经常会被省略。 可以从这张图上来自行验证一下刚才说的5条性质。 1.1、树的旋转知识 当我们在对红黑树进行插入和删除等操作时，也就是树的结点个数发生变化，那么就可能会导致红黑树不再满足性质。 为了继续保持红黑树的性质，我们可以通过对结点进行重新着色，以及对树进行相关的旋转操作，也就是通过修改树中某些结点的颜色及指针结构，来保证对红黑树进行插入或删除结点等操作后，能继续保持它的性质或保持平衡。 树的旋转，分为左旋和右旋，这两种旋转是对称的，我们以右旋为例看一下旋转的过程，下面这张图在p结点上做右旋操作： 
我们来简单总结一下这个过程： 当在一个结点上做右旋操作时，需要移动的两个单分别为：该结点和该结点的右子结点，以及该结点的左子节点和左子结点的左子结点。这两个单做顺时针旋转。 左旋和右旋对称，是逆时针旋转： 
我们来看一下旋转的伪代码： 对于树的旋转，能保持不变的只有原树的搜索性质，而原树的红黑性质则不能保持，在红黑树的数据插入和删除后可利用旋转和颜色重涂来恢复树的红黑性质。 今天的文章就到这里，下一篇文章我们重点来说红黑树对于插入查找的优化。 我是阿呆，公号【Coder阿呆】，我，及时干货内容。
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/51091.html
