图像的fft_fft算法FFT(快速傅里叶变化) 介绍&相关应用1.前言本人有幸在算法学习过程中接触该算法 , 在了解算法背后的原理后 , 不禁为先人的巧妙设计感到倾佩.不管以后是算法竞赛还是项目研究 , FFT是一种多领域的、十分常用的多项式乘积优化算法.就本人的理解 , 在这里写下一篇文章好好介绍
FFT(快速傅里叶变化) 介绍&相关应用 1.前言 本人有幸在算法学习过程中接触该算法 , 在了解算法背后的原理后 , 不禁为先人的巧妙设计感到倾佩. 不管以后是算法竞赛还是项目研究 , FFT是一种多领域的、十分常用的多项式乘积优化算法. 就本人的理解 , 在这里写下一篇文章好好介绍这种算法. 2.问题的产生 我们思考这么一个问题: 对于给定的两个多项式
 与
与
 , 试计算
, 试计算
 显然 , 我们可以计算出
显然 , 我们可以计算出
 中
中
 项的系数
项的系数
 , 就可以确定
, 就可以确定
 的表达式 根据幂运算 ,
的表达式 根据幂运算 ,
 我们可以用一层循环枚举
我们可以用一层循环枚举
 , 然后再用一层循环枚举
, 然后再用一层循环枚举
 , 即可确定所有
, 即可确定所有
 显然这种算法的时间复杂度为
显然这种算法的时间复杂度为
 (因为每个
(因为每个
 要与所有
要与所有
 乘一次) 当
乘一次) 当
 的数量级很大时,这种算法的计算效率显然会比较低. 有没有任何方法降低计算的时间复杂度呢? 3.重新整理思考方向 我们不妨从确定函数的方式上做文章. 在数值分析这门课程上 , 我们知道 , 任何一个
的数量级很大时,这种算法的计算效率显然会比较低. 有没有任何方法降低计算的时间复杂度呢? 3.重新整理思考方向 我们不妨从确定函数的方式上做文章. 在数值分析这门课程上 , 我们知道 , 任何一个
 次多项式函数都可以由平面中
次多项式函数都可以由平面中
 个横坐标互异的点个唯一确定. 因此 , 如果我们可以找到函数
个横坐标互异的点个唯一确定. 因此 , 如果我们可以找到函数
 上任意
上任意
 个互不重合的点,那么我们就可以确定唯一的
个互不重合的点,那么我们就可以确定唯一的
 但是 , 如果我们仅仅就是随便选取互不相等的
但是 , 如果我们仅仅就是随便选取互不相等的
 , 然后计算
, 然后计算
 ,并用
,并用
 来间接表示
来间接表示
 ,我们的时间复杂度还是保持在
,我们的时间复杂度还是保持在
 的水平,仿佛问题又回到了原点. 真的回到了原点嘛?我们不妨思考这样一个问题: 现在有一个程序内载
的水平,仿佛问题又回到了原点. 真的回到了原点嘛?我们不妨思考这样一个问题: 现在有一个程序内载
 次多项式偶函数
次多项式偶函数
 ,它能够输出每次输入的值对应的函数值,那么,你至少需要输入几次数据,根据它的输出,才能保证得出具体的表达式? 答案是
,它能够输出每次输入的值对应的函数值,那么,你至少需要输入几次数据,根据它的输出,才能保证得出具体的表达式? 答案是
 次,这是因为如果我们算出了
次,这是因为如果我们算出了
 的值,那么根据偶函数的性质,可以得到图像上必有
的值,那么根据偶函数的性质,可以得到图像上必有
 两点 显然这点对于奇函数也是成立的,对于奇函数
两点 显然这点对于奇函数也是成立的,对于奇函数
 ,如果我们算出了
,如果我们算出了
 ,那么图像上必有
,那么图像上必有
 两点 那我们可不可以利用这种奇偶性质来简化原问题中
两点 那我们可不可以利用这种奇偶性质来简化原问题中
 计算过程呢? 4.深入思考与推导 对于待确定函数
计算过程呢? 4.深入思考与推导 对于待确定函数
 (
(
 为奇数) 可以改写为
为奇数) 可以改写为
 即
即
 上式中,
上式中,
 都可以看作自变量
都可以看作自变量
 的多项式函数,即
的多项式函数,即

 这意味着,如果我们能算出两个子多项式
这意味着,如果我们能算出两个子多项式
 ,
,
 的在
的在
 处的函数值
处的函数值
 那么原多项式
那么原多项式
 在
在
 可以这样导出:
可以这样导出:

 注意到
注意到
 都是关于
都是关于
 的偶函数,因此,我们通过计算出两个子多项式上的两点
的偶函数,因此,我们通过计算出两个子多项式上的两点
 ,实际上可以通过上式子导出
,实际上可以通过上式子导出
 上的两个点:
上的两个点:

 将子多项式看作
将子多项式看作
 的函数,两个子多项式的次数都是
的函数,两个子多项式的次数都是
 ,这意味着我们只需要解决两个规模更小的子问题即可以解决原问题 仔细观察,两个子多项式仍然是多项式,除了次数规模与原问题不一样外基本一致,这意味着我们可以按照上述方法继续递归求解两个子多项式. 形式化地说,整个算法的解决思路如下:
,这意味着我们只需要解决两个规模更小的子问题即可以解决原问题 仔细观察,两个子多项式仍然是多项式,除了次数规模与原问题不一样外基本一致,这意味着我们可以按照上述方法继续递归求解两个子多项式. 形式化地说,整个算法的解决思路如下:
 要解决
要解决
 次多项式问题
次多项式问题
 ,相当于先解决两个
,相当于先解决两个
 的子问题,然后利用子问题的计算结果计算原问题. 这样做的时间复杂度是多少呢? 设求解
的子问题,然后利用子问题的计算结果计算原问题. 这样做的时间复杂度是多少呢? 设求解
 次多项式的时间规模为
次多项式的时间规模为
 那么由上述思路,必有
那么由上述思路,必有
 (这里加
(这里加
 是因为有
是因为有
 个点由两个子问题计算结果推导得出) 显然
个点由两个子问题计算结果推导得出) 显然
 (
(
 次多项式是一条水平直线,其值恰好等于唯一点的纵坐标) 所以
次多项式是一条水平直线,其值恰好等于唯一点的纵坐标) 所以
 由于
由于
 ,即
,即
 后面的括号中有
后面的括号中有
 项. 所以
项. 所以
 也就是说,这种做法的时间复杂度应该是
也就是说,这种做法的时间复杂度应该是
 ,明显优于我们之前的朴素暴力解法. 5.新问题的产生&解决 貌似我们的问题得以解决了,但是新的问题产生了. 对于多项式
,明显优于我们之前的朴素暴力解法. 5.新问题的产生&解决 貌似我们的问题得以解决了,但是新的问题产生了. 对于多项式
 拆分得到的
拆分得到的
 不能利用奇偶性质选取正负点对,这是因为
不能利用奇偶性质选取正负点对,这是因为
 这意味着,如果我们要将上述算法继续递归进行的话,我们有必要将自变量从实数范围扩展到复数范围内 拿待确定多项式
这意味着,如果我们要将上述算法继续递归进行的话,我们有必要将自变量从实数范围扩展到复数范围内 拿待确定多项式
 举例,将其转化为
举例,将其转化为
 令
令
 ,也就是要确定子函数
,也就是要确定子函数
 上的点 继续进行拆分:
上的点 继续进行拆分:

 根据算法,对于
根据算法,对于
 这四个
这四个
 次多项式,此时可以直接任意取横坐标求得点. 但如果我们取横坐标形如
次多项式,此时可以直接任意取横坐标求得点. 但如果我们取横坐标形如
 这样的点,那么就会出现一个问题:
这样的点,那么就会出现一个问题:
 我们当初设
我们当初设
 ,当
,当
 时,
时,
 在实数范围内无解! 因此我们必须将数域扩展到复数并选取复数正负点对,以保证算法的正确进行,在这个例子中我们在四个
在实数范围内无解! 因此我们必须将数域扩展到复数并选取复数正负点对,以保证算法的正确进行,在这个例子中我们在四个
 函数上分别取横坐标
函数上分别取横坐标
 这样可以算得
这样可以算得



 根据上述方程,推导出
根据上述方程,推导出
 上的点:
上的点:

 最后导出
最后导出
 上的点:
上的点:

 这个算法对于求解
这个算法对于求解
 次多项式
次多项式
 ,更为一般性的方法应该是这样的: ·找到最小的整数
,更为一般性的方法应该是这样的: ·找到最小的整数
 ,满足
,满足
 ·对于每次取点计算,自变量选取
·对于每次取点计算,自变量选取
 ,其中
,其中
 ,即方程
,即方程
 在复平面内按辐角排列的第
在复平面内按辐角排列的第
 个解 ·按照递归思路,利用上述方法可以求出原函数
个解 ·按照递归思路,利用上述方法可以求出原函数
 上的
上的
 个不同的点 6.关于单位根的疑问与解答 看了,上面的算法描述,好像确实是这么回事,但为什么要这样设计? 我们从横坐标的选取入手,不难看出,样例中换
个不同的点 6.关于单位根的疑问与解答 看了,上面的算法描述,好像确实是这么回事,但为什么要这样设计? 我们从横坐标的选取入手,不难看出,样例中换
 之后,如果不对数域进行扩展,那么解决两个子问题产生的点会有一半用不上.更为形式化的说,我们必须找到一个极小横坐标集合
之后,如果不对数域进行扩展,那么解决两个子问题产生的点会有一半用不上.更为形式化的说,我们必须找到一个极小横坐标集合
 ,使得对于
,使得对于
 成立,才能保证所有子多项式的计算结果可以被重复利用,达到优化效果.
成立,才能保证所有子多项式的计算结果可以被重复利用,达到优化效果.
 在复数域内的解集合是恰好满足这个性质的. 这是因为
在复数域内的解集合是恰好满足这个性质的. 这是因为
![图像的fft_fft算法插图185 \forall j \in[0,2^N-1],w_j^2=(e^{\frac{2j\pi}{2^N}i})^2=e^{\frac{4j\pi}{2^N}i}](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 而
而
 ,所以
,所以
 利用上面这一点性质可推出
利用上面这一点性质可推出
 (
(
 的意思表示求模),而
的意思表示求模),而
![图像的fft_fft算法插图195 2j\%2^N \in [0,2^N-1]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 因此满足我们需求的性质. 7.问题剩下的一半? 那我们现在求出了
因此满足我们需求的性质. 7.问题剩下的一半? 那我们现在求出了
 个不同的点,那我们该如何求出待求
个不同的点,那我们该如何求出待求
 次多项式
次多项式
 呢? 经过上述算法操作,对于多项式
呢? 经过上述算法操作,对于多项式
 ,我们找到了它上面的
,我们找到了它上面的
 个点
个点
 相当于确定了一个
相当于确定了一个
 一次方程组.
一次方程组.
 根据线性代数的知识,可以写成如下形式:
根据线性代数的知识,可以写成如下形式:
 其中:
其中:
![图像的fft_fft算法插图207 \bold c=[c_0,c_1,···,c_{N-1}]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E)
 ,显然这也是范德蒙矩阵
,显然这也是范德蒙矩阵
![图像的fft_fft算法插图211 \bold f=[f(w_0),f(w_1)···,f(w_{N-1})]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 我们相当于要求出
我们相当于要求出
 ,即求出
,即求出
 到这里,FFT最为巧妙的一点来了,我们只需要把所求
到这里,FFT最为巧妙的一点来了,我们只需要把所求
 个点的纵坐标构造函数
个点的纵坐标构造函数
 ,然后以横坐标点集
,然后以横坐标点集
 ,求出
,求出
 上的
上的
 个点即可,
个点即可,
 (这样做的原因涉及到离散数学中的对偶、线性代数中范德蒙矩阵的逆等问题,这里不再细究.) 这意味着我们算法思路与大体框架不变,可以仅仅通过修改参数的方式实现多项式系数的求解. 8.算法总结&代码实现 综上分析,我们来总结一下解决问题的算法:
(这样做的原因涉及到离散数学中的对偶、线性代数中范德蒙矩阵的逆等问题,这里不再细究.) 这意味着我们算法思路与大体框架不变,可以仅仅通过修改参数的方式实现多项式系数的求解. 8.算法总结&代码实现 综上分析,我们来总结一下解决问题的算法:
 系数
系数
 点:(也叫FFT正变换) ·对于两个多项式
点:(也叫FFT正变换) ·对于两个多项式
 ,找到最小的整数
,找到最小的整数
 ,使得
,使得
 M+N-2″ eeimg=”1″> ·利用第5点中的取点算法,分别求出
M+N-2″ eeimg=”1″> ·利用第5点中的取点算法,分别求出
 上的
上的
 个点坐标(横坐标取值依次为
个点坐标(横坐标取值依次为
 ),时间复杂度为
),时间复杂度为

 中间过渡 ·由
中间过渡 ·由
 上的
上的
 个点坐标,算出目标函数
个点坐标,算出目标函数
 上对应的
上对应的
 个点坐标,即
个点坐标,即
 ,时间复杂度为
,时间复杂度为

 点
点
 系数:(也叫FFT逆变换) ·构造
系数:(也叫FFT逆变换) ·构造
 ,按照第7点中的方法逆向求出
,按照第7点中的方法逆向求出
 中的系数,时间复杂度为
中的系数,时间复杂度为
 综上分析,时间复杂度为
综上分析,时间复杂度为
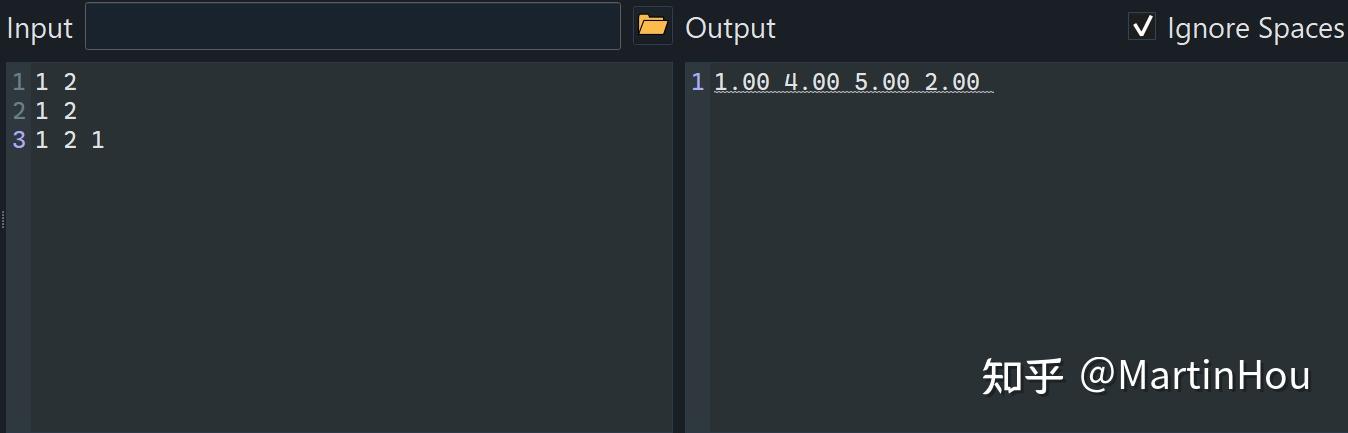
 代码(C++) 你可以自己测试一下这段代码,输入标准如下: 第一行是两个整数
代码(C++) 你可以自己测试一下这段代码,输入标准如下: 第一行是两个整数
 ,分别表示
,分别表示
 的最高次项. 第二行有
的最高次项. 第二行有
 个实数,第
个实数,第
 个数表示
个数表示
 的
的
 次项系数
次项系数
 第三行有
第三行有
 个实数,第
个实数,第
 个数表示
个数表示
 的
的
 次项系数
次项系数
 如果你的输入无误,那么应该会得到
如果你的输入无误,那么应该会得到
 个实数输出,从左到右第
个实数输出,从左到右第
 个数表示目标函数
个数表示目标函数
 的
的
 次项系数
次项系数
 例如: 输入: 输出:
例如: 输入: 输出:

 表示函数
表示函数
 与
与
 的乘积为
的乘积为
 9. 应用领域 FFT算法的应用领域十分广阔. ·大数乘法 对于任何一个数字,我们都可以将其写成一个多项次形式,例如
9. 应用领域 FFT算法的应用领域十分广阔. ·大数乘法 对于任何一个数字,我们都可以将其写成一个多项次形式,例如
 因此对于两个大数乘法,我们可以先将它们对应的多项式形式写出来,然后利用FFT算法进行函数乘积,最后令目标函数中的自变量为
因此对于两个大数乘法,我们可以先将它们对应的多项式形式写出来,然后利用FFT算法进行函数乘积,最后令目标函数中的自变量为
 即可得到答案,这种做法比朴素竖式乘法快很多. 例如,要计算
即可得到答案,这种做法比朴素竖式乘法快很多. 例如,要计算
 可以将
可以将
 同理
同理
 计算出
计算出
 ,
,
 即是乘积 目前这种做法被运用于大数相乘,如Java BigInt类 与Python 自带的高精度. ·波形分解 无论是地震波还是声波,它们在一定时间内可以看作是周期函数,利用FFT算法,我们可以从总分解得到这些波形的构成,或者更为专业地说,一组正弦函数正交基.以便我们用于对波形进行分析、预测、处理. 详情可见:【官方双语】形象展示傅里叶变换_哔哩哔哩_bilibili ·图像处理 利用FFT算法处理图像,可以获知图中每个点在灰度空间地变化频率,图像上某一点与邻域点灰度值差异的强弱,即梯度的大小,也即该点的频率的大小(差异/梯度越大,频率越高,能量越低,在频谱图上就越 暗。差异/梯度越小,频率越低,能量越高,在频谱图上就越 亮。换句话说,频率谱上越亮能量越高,频率越低,图像差异越小/平缓)。一般来讲,梯度大则该点的亮度强,否则该点亮度弱。 多用于训练集的提前处理.
即是乘积 目前这种做法被运用于大数相乘,如Java BigInt类 与Python 自带的高精度. ·波形分解 无论是地震波还是声波,它们在一定时间内可以看作是周期函数,利用FFT算法,我们可以从总分解得到这些波形的构成,或者更为专业地说,一组正弦函数正交基.以便我们用于对波形进行分析、预测、处理. 详情可见:【官方双语】形象展示傅里叶变换_哔哩哔哩_bilibili ·图像处理 利用FFT算法处理图像,可以获知图中每个点在灰度空间地变化频率,图像上某一点与邻域点灰度值差异的强弱,即梯度的大小,也即该点的频率的大小(差异/梯度越大,频率越高,能量越低,在频谱图上就越 暗。差异/梯度越小,频率越低,能量越高,在频谱图上就越 亮。换句话说,频率谱上越亮能量越高,频率越低,图像差异越小/平缓)。一般来讲,梯度大则该点的亮度强,否则该点亮度弱。 多用于训练集的提前处理.
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。
文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/46521.html





















































































































![图像的fft_fft算法插图185 \forall j \in[0,2^N-1],w_j^2=(e^{\frac{2j\pi}{2^N}i})^2=e^{\frac{4j\pi}{2^N}i}](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)




![图像的fft_fft算法插图195 2j\%2^N \in [0,2^N-1]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)









![图像的fft_fft算法插图207 \bold c=[c_0,c_1,···,c_{N-1}]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)

![图像的fft_fft算法插图211 \bold f=[f(w_0),f(w_1)···,f(w_{N-1})]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)