fft 计算_fft算法有什么用

请问为什么fft可以加速卷积运算？　　我们知道对
点的序列
x(n) 和M点的序列
h(n) 计算卷积，可以先将
x(n) 补零为
N+M-1 点
$\tilde x(n)$ ，以及将
h(n) 补零为
N+M-1 点
$\tilde h(n)$ ，然后计算它们的DFT函数（用fft实现）：
$\tilde X(k)$ 和
$\tilde H(k)$ ，然后将它们乘起来再计算IDFT（用ifft实现）。　　但问题来了：为什么变换到频域进行fft计算再变换回来会加快运算速度？　　可能大家没有明白我的疑惑在哪里，这里我以N=M=4举个例子。　　计算它们卷积相当于计算反对角线的求和，如下图所示，矩阵里面的素没有任何重复的，而仅仅是计算矩阵的素都已经需要执行
o(N^2) 次乘法运算了。为什么转换到频域进行fft运算后却只需要执行
$o(N \log N)$ 量级的运算呢？
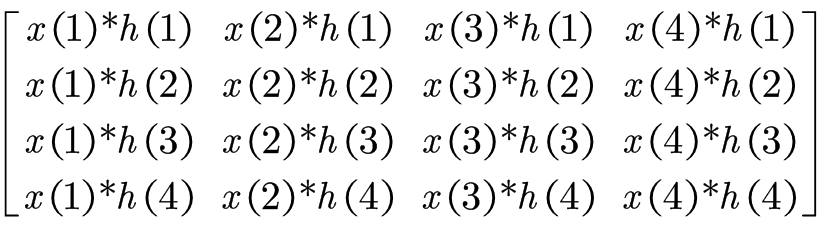　　当然从结果反推过程的思路来想，或许会有一个答案：因为素虽然不重复，但是彼此之间有关联，利用这些关联就会让我们不需要执行这么多运算。或者有答主可能会说因为fft的定义是：　　
$\displaystyle X(k)=\sum_{n=0}^{N-1}x(n)\,W_N^{kn}$ 　　而
W_N 因子的周期性、对称性使得我们可以通过奇偶拆分函数，最后通过递归降阶问题从而降低运算复杂度。但我认为这些都是知道答案反推过程合理性的方法，并没有指出这种运算为什么“正向地”合理。　　打个比方，假设你看到卷积定义
$y(n)=\sum_kx(k)h(n-k)$ ，然后看到计算过程竟然是　　
$y(n)=\sum_kx(k)h(n-k)=\frac1N\sum_m\left(\left(\sum_k\tilde x(k)\,W_N^{km}\right)\left(\sum_k\tilde h(k)\,W_N^{km}\right)W_N^{-mn}\right)$ 　　一定会觉得这个过程很不可思议。一方面是为什么实数运算突然就变到了复数运算，另一方面是疑惑这些奇妙的构造是什么原理？确切地说，我的疑惑就在于这里——为什么通过频域的计算，我们就能加快卷积计算？
N^2 次乘法运算时究竟如何被偷天换日为了
$N \log N$ ，这一运算复杂度是如何被吸收掉的。再换一个可能更深甚至没有答案的问题，既然是实数的运算，我们能不能通过实数本身的某种递归降阶的运算方式加速计算，而不借助频域的帮助。　　当然，我的想法是：频域可能和卷积运算具有某种特定联系，这种联系将会使得卷积这种运算在频域中具有什么特性。但问题在于：这种特定联系究竟是什么？如果说傅里叶变换的卷积性质就有一点事后诸葛亮的感觉了。而且即使如此，我还是没有明白为什么这种特性会让我们减少运算次数，是否有更加本质（正向推导）的原因，而不是使用
W_N 因子的周期性、对称性这种由结果导出过程的解释。　　那卷积肯定是有其特殊性的，首先我们看它的结构是输出函数的每个点都是原先的两个函数相乘再积分，这种运算是不是有点向量乘以矩阵的感觉，函数f是一个向量，函数g经过不同的平移之后形成一个矩阵，卷积就类似于向量乘以矩阵这样？对于离散的情况来说，那就更是这样了，完完全全就是一个矩阵乘法。　　一般来说一个向量乘以矩阵（记为Ax）应该是个O(n^2)的过程。但是，如果这个矩阵是个对角阵，或者可以比较容易地对角化，也就是：　　A=Q^T A’ Q 　　其中Q是一个单位正交阵，那么就有　　Ax = Q^T A’ (Qx) 　　如果又那么巧，Q或Q^T乘以一个向量有个快速算法，那么先算Qx，再算和一个对角阵的乘积，再算一个逆变换，就有意义了。　　那么如何将A对角化呢？我们大致知道可以求它的特征向量，也就是求各种u使得Au=λu，其中u是个向量而λ是个常数。而对于卷积运算来说，很巧，exp(iωx)就是这个特征向量，任何函数和exp(iωx)卷积，都会得到exp(iωx)的常数倍，这样我们真的可以做到将这个卷积对应的矩阵对角化了，而且这组特征向量甚至和卷积函数本身无关。更巧的事情在于，对于2^k阶的矩阵来说，这个正交阵Q与向量的乘法还真的就是有快速运算的方法，也就是FFT。这样就真的可以将卷积用FFT来提速了。　　所以可以看出，卷积运算的特殊性在于有固定的特征向量，因而可以稳定地对角化，从而将矩阵乘法转换为乘以对角阵。　　以4维为例，向量卷积
$x\ast y$ 相当于如下运算：　　
$\begin{bmatrix} x_1&x_4&x_3&x_2\\ x_2&x_1&x_4&x_3\\ x_3&x_2&x_1&x_4\\ x_4&x_3&x_2&x_1\\ \end{bmatrix} \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}$ 　　这个本来是
O(n^2) ，但是前面这个矩阵有个名字叫 circulant matrix. 它的特殊之处在于其特征向量的方向与
的值无关，而其特征值又是
的DFT结果，　　对它对角化之后得到
$Q\Lambda Q^T$ ，这个
Q^T ，也就是由其特征向量并排组成的矩阵，刚好是一个DFT矩阵，所以可以用FFT加速到
。　　题主那个关于“实数”的问题，答案是不行，不能对角化的矩阵就肯定免谈了，就算是一般的hermitian矩阵正交对角化，得到的
Q^T 并不符合被FFT加速的性质。你写出来的那个很长的公式，只不过是把
$Q\Lambda Q^Ty$ 用
O(n^2) 在暴力算而已。　　题主如果想了解卷积和傅立叶变换之间到底有什么关系，想想这个问题：　　已知
的傅立叶级数，如何求
的傅立叶级数？　　你的直觉是对的，直接计算傅里叶根本不能加速。加速的原理是有种东西叫快速傅里叶变换，能把傅里叶变换的过程从N方变NlogN，所以就加速了。　　这个问题很简单~ 　　下面我们只考虑圆周卷积的情况， * 代表圆周卷积，　　对于一维列向量，a 和 b，假设c = a*b 　　由于卷积是一个有限维度的线性运算，那么可以表达为矩阵向量的乘法形式　　
$c = Mb\\$ 　　这里面 M 是一个 Circulant Matrix，而Circulant Matrix 是一种特殊的 Toeplitz Matrix 可以被 DFT Matrix 对角化。
$M = F^H \Lambda F\\$ 　　那么　　
$c = Mb = F^H \Lambda F b\\$ 　　从右往左看这里面
是b 的傅里叶变换，
$\Lambda (Fb)$ 是逐点相乘，FLOPS很便宜，
$F^H(\Lambda(Fb))$ 是逆傅里叶变换。这里面由于傅里叶变换的属性，我们存在快速解法， MIT 著名线性代数教授Gilbert Strang 曾经描述过FFT 算法可能是我们一生当中最重要的数值方法，他从
O(n^2) 降低到了
$O（n\log n)$ 。这样子我们每一步都能有一个比较省flops 的操作，那么整体上我们能够有一种相对快的方法。　　但是实际生活当中用zero padding FFT 作快卷积，不一定快，尤其是当卷积一方比较小的时候，或者为了满足类似
2^n 这样的 zero padding使得padding 长度过大，那么fft 做卷积都是慢的。只有当两者长度可比拟时候fft的优势才能体现出来。　　所以由此延伸出更好的overlap discard， overlap save等快速卷积方法，可以改善上述问题： https://en.wikipedia.org/wiki/Overlap%E2%80%93save_method 　　备注 1： FFT 其实是一种特殊的范德蒙矩阵，范德蒙矩阵的一类子集都存在矩阵向量相乘的快速数值方法，比如Fast Walsh Hadmard Transform等 https://en.wikipedia.org/wiki/Fast_Walsh%E2%80%93Hadamard_transform 　　备注 2：但是!但是！所有上述推导都是纯理论的flops比较，但是实际上flops小的速度并不一定快！！！！我的数值线性代数教授反复给我们强调过这一点！！！！　　是否能够减少overhead，还有能否充分调用CPU/GPU 性能，是否高度可并行化很多时候才能在实际生活中真正决定速度，纸上得来终觉浅哈，理论固然重要，但是不要轻易相信任何数值方法给的结论，最重要的是真的在实际生活中在对应的硬件软件平台上跑一跑才知道的。　　太长不看版　　定义序列
$a=\left\{a_0,a_1,\cdots,a_{n-1}\right\}$ 的离散傅里叶变换（DFT）是序列
$y=\left\{y_0,y_1,\cdots,y_{n-1}\right\}$ ，其中，　　
$y_k=\sum_{j=0}^{n-1}{a_j\omega_n^{kj}}$ 暂时忽略
$\omega_n$ 的具体值，目前不影响理解。　　序列
的逆变换（iDFT）是序列
$\tilde{a}=\left\{\tilde{a}_0,\tilde{a}_1,\cdots,\tilde{a}_{n-1}\right\}$ ，其中，　　
$\tilde{a}_k=\frac{1}{n}\sum_{j=0}^{n-1}{y_j\omega_n^{-kj}}$ 可以验证
$\tilde{a}_k=a_k$ 。　　如果用最朴素的方法计算DFT与iDFT，代价是
O(n^2) ；但是利用
$\omega_n$ 这个数的特殊性质，可以设计出高效的分治算法——FFT与iFFT，能在
$O(n\log{n})$ 时间内计算出DFT与iDFT。
$\omega_n$ 与FFT的详细介绍在“明星登场”部分。　　现在给定两个序列：
$a=\left\{a_0,a_1,\cdots,a_{n-1}\right\}$ ，
$b=\left\{b_0,b_1,\cdots,b_{n-1}\right\}$ ，他们的DFT：　　
$y_k=\sum_{j=0}^{n-1}{a_j\omega_n^{kj}}$ 　　
$y'_k=\sum_{j=0}^{n-1}{b_j\omega_n^{kj}}$
$\left\{y_k\right\}_{k=0}^{n-1}$ 与
$\left\{y'_k\right\}_{k=0}^{n-1}$ 的具体值可以用FFT在
$O(n\log{n})$ 时间内得到。　　计算乘积：　　
$y_ky'_k=\left(\sum_{j=0}^{n-1}{a_j\omega_n^{kj}}\right)\left(\sum_{j=0}^{n-1}{b_j\omega_n^{kj}}\right)$
$\left\{y_ky'_k\right\}_{k=0}^{n-1}$ 的具体值可以在
O(n) 时间内得到。　　如果令
$x=\omega_n^k$ ，那么，　　
$y_ky'_k=\left(\sum_{j=0}^{n-1}{a_jx^j}\right)\left(\sum_{j=0}^{n-1}{b_jx^j}\right)$ 　　这是两个多项式的乘积。所以有，　　
$y_ky'_k=\sum_{j=0}^{n-1}{\left(\sum_{t=0}^j{a_tb_{j-t}}\right)\omega_n^{kj}}$ 我们发现DFT与多项式乘积之间存在关联，因此正文“问题引入”部分从多项式乘积开始讲起，“头脑风暴”部分给出了该问题的建模方法。　　然后计算逆变换，即可得到：　　
$c_k=\frac{1}{n}\sum_{j=0}^{n-1}{y_jy'_j\omega_n^{-kj}}=\sum_{t=0}^k{a_tb_{k-t}}$ 逆变换可以用iFFT在
$O(n\log{n})$ 时间内得到。　　序列
$c=\left\{c_0,c_1,\cdots,c_{n-1}\right\}$ 就是序列
与序列
的卷积，整个过程的时间复杂度是
$O(n\log{n})$ 。频域可能和卷积运算具有某种特定联系，……，这种特定联系究竟是什么？　　其实就是一句耳熟能详的话：时域卷积=频域乘积。　　以上说明比较简略，想了解细节，可以继续阅读。分割线以下开始正文内容。注：正文内容整理自《算法导论》。　　问题引入　　有多项式：　　
$A(x)=\sum_{j=0}^{n-1}{a_j x^j}$ 　　
$B(x)=\sum_{j=0}^{n-1}{b_j x^j}$ 　　计算多项式乘积：　　
$C(x)=A(x)B(x)=\sum_{j=0}^{n-1}{c_j x^j}$ 　　其中，　　
$c_j=\sum_{k=0}^j{a_k b_{j-k}}$ 补零的部分大家应该都懂吧。比如，计算1次多项式
（
$a_1\ne 0$ ）与2次多项式
（
$b_2\ne0$ ）的乘积，结果肯定是3次多项式：
（
$c_3\ne0$ ），此时我们可以对多项式
和多项式
进行补零，得到
和
。　　头脑风暴　　若要直接计算，复杂度显然是
O(n^2) 。计算
c_j 一个数的复杂度是
O(n) ，如果直接计算
$\left\{c_j\right\}_{j=0}^{n-1}$ 共
个数，复杂度当然是
O(n^2) 。　　可是，真的只能直接计算吗？回答是否定的。　　先引入一个概念——多项式的表示。　　对于多项式
$A(x)=\sum_{j=0}^{n-1}{a_j x^j}$ ，我们可以用
$a=(a_0,a_1,\cdots,a_{n-1})$ 来唯一确定多项式
，因为
a_j 是多项式的系数，所以称
$a=(a_0,a_1,\cdots,a_{n-1})$ 是多项式
的系数表示。　　那多项式有没有其他的表示方法呢？　　假设我们取
个互不相同的值
$x=(x_0,x_1,\cdots,x_{n-1})$ ，然后将这些值带入多项式
，就可以得到
个点
$\left\{(x_0,y_0),(x_1,y_1),\cdots,(x_{n-1},y_{n-1})\right\}$ ，其中
。现在问一个问题：这
个点能不能（反过来）唯一确定多项式
（的系数
）？　　（建议想5秒钟再看）　　该问题就变成了求解
线性方程组了：　　
$\begin{pmatrix} 1 & x_0 & x_0^2 & \cdots & x_0^{n-1} \\ 1 & x_1 & x_1^2 & \cdots & x_1^{n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 1 & x_{n-1} & x_{n-1}^2 & \cdots & x_{n-1}^{n-1} \end{pmatrix} \begin{pmatrix} a_0 \\ a_1 \\ \vdots \\ a_{n-1} \end{pmatrix}=\begin{pmatrix} y_0 \\ y_1 \\ \vdots \\ y_{n-1} \end{pmatrix}$ 　　（别搞错了，
才是未知数）　　这个方程组解的情况如何？答：存在唯一解。　　因为最左边的矩阵是范德蒙（或者叫“范德蒙德”）矩阵，其行列式的值是：　　
$\prod_{0\le k<j\le n-1}{x_j-x_k}$ 　　又因为
$x=(x_0,x_1,\cdots,x_{n-1})$ 互不相同，所以行列式的值不等于零，即方程组存在唯一解。如果你对唯一解的部分存在疑问，可以回顾《线性代数》。　　到这里，可以说我们找到了多项式的一种新的表示方法——点值表示：给定
个二维平面点
$\left\{(x_0,y_0),(x_1,y_1),\cdots,(x_{n-1},y_{n-1})\right\}$ ，横坐标
$x=(x_0,x_1,\cdots,x_{n-1})$ 互不相同，即可表示多项式
。　　下面的问题是：点值表示有没有什么优越性？　　当然有，因为如果多项式
的点值表示是
$\left\{(x_0,y_0),(x_1,y_1),\cdots,(x_{n-1},y_{n-1})\right\}$ ，而多项式
的点值表示是
$\left\{(x_0,y'_0),(x_1,y'_1),\cdots,(x_{n-1},y'_{n-1})\right\}$ （注意，
是一样的），那么多项式
的点值表示就是
$\left\{(x_0,y_0y'_0),(x_1,y_1y'_1),\cdots,(x_{n-1},y_{n-1}y'_{n-1})\right\}$ ，计算多项式
点值表示这个步骤的复杂度是
O(n) 。提示：如果已知多项式
和多项式
在
x_k 处的取值分别是
和
，那么多项式
和多项式
的乘积多项式
在
x_k 处的取值则是
。　　总结一下，我们的问题发生了转变：要将多项式
和多项式
的系数表示转换为点值表示；用
O(n) 时间求出多项式
的点值表示；将多项式
的点值表示重新转换为系数表示。　　所以新的问题是：系数表示与点值表示之间，有没有高效的转换方法？　　明星登场　　高效的转换方法就是FFT与iFFT。　　首先登场的是
次单位根
$\omega_n^k$ （
$\omega_n$ 叫做“旋转因子”，
是旋转因子的指数），该复数满足：　　
$\left(\omega_n^k\right)^n=1$ 　　这样的数共有
个（注意这些数互不相同）：　　
$\omega_n^k=e^{2k\pi i/n}$ 　　其中，
$k=0,1,\cdots,n-1$ ，
$i=\sqrt{-1}$ 。　　利用欧拉公式，　　
$e^{ix}=\cos{x}+i\sin{x}$ 　　可以知道这
个数的
次方确实等于1：　　
$\left(\omega_n^k\right)^n=e^{2k\pi i}=\cos{2k\pi}+i\sin{2k\pi}=1$ 　　下面要登场的是
$\omega_n^k$ 的一些有意思的性质：
$\omega_{dn}^{dk}=e^{2dk\pi i/dn}=e^{2k\pi i/n}=\omega_n^k$ 如果
是偶数，
$\omega_n^{n/2}=e^{2\cdot\frac{n}{2}\pi i/n}=e^{\pi i}=\cos{\pi}+i\sin{\pi}=-1$
$\omega_n^{k+n/2}=\omega_n^k\omega_n^{n/2}=-\omega_n^k$ 　　现在我们要计算：　　
$y_k=A(\omega_n^k)=\sum_{j=0}^{n-1}{a_j\omega_n^{kj}}$ 　　等等，为什么把
$\omega_n^k$ 带入
x_k ？回顾一下“问题引入”与“头脑风暴”，我们并不关心
x_k 到底是什么，只要
$x=(x_0,x_1,\cdots,x_{n-1})$ 互不相同，然后完成“系数转点值——求积——点值转系数”即可。上面的公式正是“所谓的”离散傅里叶变换（DFT）的定义式，有的地方可能旋转因子的指数和本文的差了一个负号，看到逆变换以后，你会知道这真的只是一个符号问题。　　
y_k 怎么求？每个都要花费线性时间吗？不，现在登场的是分治。　　这里增加一个限制条件：
n=2^m （
0″ eeimg=”1″> ）。　　分治不是简单的左边右边分两份，而是分奇偶，令：　　
$A^{[0]}(x)=a_0+a_2x+a_4x^2+\cdots+a_{n-2}x^{n/2-1}$ 　　
$A^{[1]}(x)=a_1+a_3x+a_5x^2+\cdots+a_{n-1}x^{n/2-1}$ 　　于是，　　
$A(x)=A^{[0]}(x^2)+xA^{[1]}(x^2)$ 　　代入
$\omega_n^k$ ，　　
$A(\omega_n^k)=A^{[0]}(\omega_n^{2k})+\omega_n^kA^{[1]}(\omega_n^{2k})$ 　　别眨眼，我们用用上面的性质1：　　
$A(\omega_n^k)=A^{[0]}(\omega_{n/2}^k)+\omega_n^kA^{[1]}(\omega_{n/2}^k)$ 　　这里人为限制
$k=0,1,\cdots,n/2-1$ 。　　那对于
$k=n/2,n/2+1,\cdots,n-1$ 怎么办？这么算：　　
$A(\omega_n^{k+n/2})=A^{[0]}\left((\omega_n^{k+n/2})^2\right)+\omega_n^{k+n/2}A^{[1]}\left((\omega_n^{k+n/2})^2\right)$ 　　继续忍住别眨眼，这次我们先用性质2，再用性质1：　　
$\begin{aligned} A(\omega_n^{k+n/2})&=A^{[0]}\left((\omega_n^{k+n/2})^2\right)+\omega_n^{k+n/2}A^{[1]}\left((\omega_n^{k+n/2})^2\right)\\ &=A^{[0]}\left((-\omega_n^k)^2\right)-\omega_n^kA^{[1]}\left((-\omega_n^k)^2\right)\\ &=A^{[0]}(\omega_n^{2k})-\omega_n^kA^{[1]}(\omega_n^{2k})\\ &=A^{[0]}(\omega_{n/2}^k)-\omega_n^kA^{[1]}(\omega_{n/2}^k) \end{aligned}$ 　　是不是看出什么东西来了？把两个公式放在一起：　　
$A(\omega_n^k)=A^{[0]}(\omega_{n/2}^k)+\omega_n^kA^{[1]}(\omega_{n/2}^k)$ 　　
$A(\omega_n^{k+n/2})=A^{[0]}(\omega_{n/2}^k)-\omega_n^kA^{[1]}(\omega_{n/2}^k)$ 　　其中，
$k=0,1,\cdots,n/2-1$ 　　这两个公式看似普通，实际上包含的信息量还不少，简单梳理一下：多项式
的规模是
（输入
个系数
$\left\{a_j\right\}_{j=0}^{n-1}$ ），根据
的奇偶分组，得到规模是
n/2 的多项式
$A^{[0]}$ 和多项式
$A^{[1]}$ 。对于规模是
的多项式
，目标是计算
$A(\omega_n^k)$ （
$k=0,1,\cdots,n-1$ ）；类似地，对于规模是
n/2 的多项式
$A^{[0]}$ 和多项式
$A^{[1]}$ ，目标是计算
$A^{[0]}(\omega_{n/2}^k)$ 和
$A^{[1]}(\omega_{n/2}^k)$ （
$k=0,1,\cdots,n/2-1$ ）。对于
$k=0,1,\cdots,n/2-1$ ，如果已经算出了
$A^{[0]}(\omega_{n/2}^k)$ 和
$A^{[1]}(\omega_{n/2}^k)$ ，那么
$A(\omega_n^k)=A^{[0]}(\omega_{n/2}^k)+\omega_n^kA^{[1]}(\omega_{n/2}^k)$ ，这样我们就得到了“前一半”的结果；只要将等式右边中间的符号改成减号，就可以得到“后一半”的结果
$A(\omega_n^{k+n/2})=A^{[0]}(\omega_{n/2}^k)-\omega_n^kA^{[1]}(\omega_{n/2}^k)$ 。这是分治的中间过程。当
n=2^0=1 时，表示仅有1项要算，直接计算即可（带入公式会发现没有东西要算，直接返回即可），这是分治的终止条件。　　在给出具体的代码之前，我们还差一个步骤，那就是如何将点值转换回系数（也就是“逆变换”）。　　回顾一下将系数转换到点值的矩阵运算（已知系数
，求
）：　　
$\begin{pmatrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega_n & \omega_n^2 & \cdots & \omega_n^{n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 1 & \omega_n^{n-1} & \omega_n^{2(n-1)} & \cdots & \omega_n^{(n-1)(n-1)} \end{pmatrix} \begin{pmatrix} a_0 \\ a_1 \\ \vdots \\ a_{n-1} \end{pmatrix}=\begin{pmatrix} y_0 \\ y_1 \\ \vdots \\ y_{n-1} \end{pmatrix}$ 注意观察最左边这个矩阵，是不是有什么特点？（我不在这里展开，只是提醒你留意一下其他答主提到的矩阵性质）　　那么点值转换回系数的矩阵运算就是（已知
，求系数
）：　　
$\begin{pmatrix} a_0 \\ a_1 \\ \vdots \\ a_{n-1} \end{pmatrix}=\begin{pmatrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega_n & \omega_n^2 & \cdots & \omega_n^{n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 1 & \omega_n^{n-1} & \omega_n^{2(n-1)} & \cdots & \omega_n^{(n-1)(n-1)} \end{pmatrix}^{-1}\begin{pmatrix} y_0 \\ y_1 \\ \vdots \\ y_{n-1} \end{pmatrix}$ 这时候逆矩阵是否存在以及具体是什么还不知道。　　令，　　
$V=\begin{pmatrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega_n & \omega_n^2 & \cdots & \omega_n^{n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 1 & \omega_n^{n-1} & \omega_n^{2(n-1)} & \cdots & \omega_n^{(n-1)(n-1)} \end{pmatrix}$ 　　
$V_{k,j}=\omega_n^{kj}$ 　　现在直接告诉你：　　
$V_{k,j}^{-1}=\omega_n^{-kj}/n$ 　　不信你可以验证一下：　　
$\begin{aligned} \left[V^{-1}V\right]_{k,j}&=\frac{1}{n}\sum_{t=0}^{n-1}{\omega_n^{-kt}\omega_n^{tj}}\\ &=\frac{1}{n}\sum_{t=0}^{n-1}{\omega_n^{t(j-k)}}\\ &=\left\{\begin{matrix}1, & k=j\\ 0, & k\ne j\end{matrix}\right. \end{aligned}$ 　　对于
$k\ne j$ ，　　
$\begin{aligned} \sum_{t=0}^{n-1}{(\omega_n^{j-k})^t}&=\frac{1-(\omega_n^{j-k})^n}{1-\omega_n^{j-k}}\\ &=\frac{1-1}{1-\omega_n^{j-k}}\\ &=0 \end{aligned}$ 上面证明的是
$V^{-1}V=I$ ，其中
是单位矩阵。　　所以，回到点值转换回系数的矩阵运算（已知
，求系数
）：　　
$\begin{pmatrix} a_0 \\ a_1 \\ \vdots \\ a_{n-1} \end{pmatrix}=\frac{1}{n}\begin{pmatrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega_n^{-1} & \omega_n^{-2} & \cdots & \omega_n^{-(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 1 & \omega_n^{-(n-1)} & \omega_n^{-2(n-1)} & \cdots & \omega_n^{-(n-1)(n-1)} \end{pmatrix}\begin{pmatrix} y_0 \\ y_1 \\ \vdots \\ y_{n-1} \end{pmatrix}$ 　　再把另一个公式搬过来（已知系数
，求
）：　　
$\begin{pmatrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega_n & \omega_n^2 & \cdots & \omega_n^{n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 1 & \omega_n^{n-1} & \omega_n^{2(n-1)} & \cdots & \omega_n^{(n-1)(n-1)} \end{pmatrix} \begin{pmatrix} a_0 \\ a_1 \\ \vdots \\ a_{n-1} \end{pmatrix}=\begin{pmatrix} y_0 \\ y_1 \\ \vdots \\ y_{n-1} \end{pmatrix}$ 　　我们能用FFT，根据系数
，求出
。那么现在，只要新的旋转因子
$\omega_n^{-k}$ 拥有类似
$\omega_n^k$ 的一些性质（就是性质1和性质2，而且显然
$\omega_n^{-k}$ 也有类似的性质），我们就能修改FFT，得到iFFT，可以根据
，求出系数
。实际上，直接修改FFT（旋转因子的指数增加负号），得到的是
，所以iFFT的最后一步是整体除掉
。　　Python代码：　　简单分析一下的时间复杂度，假设的时间复杂度是
T(n) ，其中
是输入规模。当
n=1 时，直接返回，因此
。当
1″ eeimg=”1″> 时，首先在规模减半的数据上递归调用2次，再是一个循环，所以代价是
$T(n)=2T\left(\frac{n}{2}\right)+O(n)$ 。有了递推公式，不断代入
$T\left(\frac{n}{2}\right)$ 、
$T\left(\frac{n}{2^2}\right)$ 、……、
，不难得到FFT与iFFT的时间复杂度是
$O(n\log{n})$ 。通俗来说，因为每次递归调用的输入规模减半，所以递归深度是
$O(\log{n})$ ，又因为递归过程中还包含
O(n) 的操作，所以时间复杂度是
$O(n\log{n})$ 。　　上面的代码展示了求多项式乘积的一般方法：先将多项式
和多项式
的系数转换为点值，其代价是
$O(n \log{n})$ ；计算多项式
的点值，代价是
O(n) ；最后将多项式
的点值转换回系数，代价是
$O(n\log{n})$ ，所以整体代价就是
$O(n\log{n})$ 。注意：本文的实现代码仅仅是示意，真正的FFT有很多优化，比如不可能这么频繁地分配内存空间。　　完结，撒花！　　参考　　算法导论（第三版）acm-scl/fft.md at master · JonathanSilver/acm-scl (github.com)

fft 计算_fft算法有什么用

相关推荐