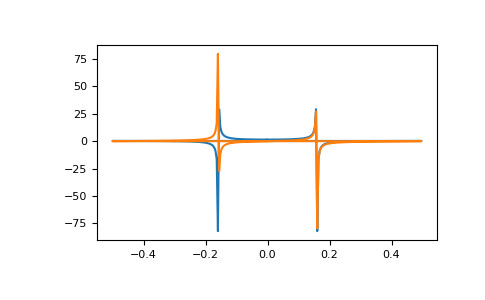
Python numpy fft.fft用法及代码示例 本文简要介绍 python 语言中 的用法。 用法: 计算一维离散傅里叶变换。 此函数使用高效的快速傅里叶变换 (FFT) 算法 [CT] 计算一维 n-point 离散傅里叶变换 (DFT)。 参数: a: array_like 输入数组,可以很复杂。 n: 整数,可选 输出的变换轴的长度。如果 n 小于输入的长度,则裁剪输入。如果它更大,则用零填充输入。如果未给出 n,则使用沿轴指定的轴的输入长度。 axis: 整数,可选 计算 FFT 的轴。如果未给出,则使用最后一个轴。 norm: {“backward”, “ortho”, “forward”},可选 标准化模式(参见 )。默认为“backward”。指示前向/后向变换对的哪个方向被缩放以及使用什么归一化因子。 返回: out: 复杂的ndarray 截断或补零的输入,沿轴指示的轴转换,如果未指定轴,则为最后一个。 抛出: IndexError 如果axis不是a的有效轴。 注意: FFT(快速傅里叶变换)是指通过在计算项中使用对称性,可以有效计算离散傅里叶变换 (DFT) 的一种方式。当 n 是 2 的幂时,对称性最高,因此对于这些大小,变换是最有效的。 在 模块的文档中定义了 DFT,以及此实现中使用的约定。 参考: CT: Cooley、James W. 和 John W. Tukey,1965 年,“复杂傅里叶级数的机器计算算法”,数学。计算。 19:297-301。 例子: 在此示例中,实输入具有 Hermitian 的 FFT,即实部对称而虚部反对称,如 文档中所述:
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/30988.html