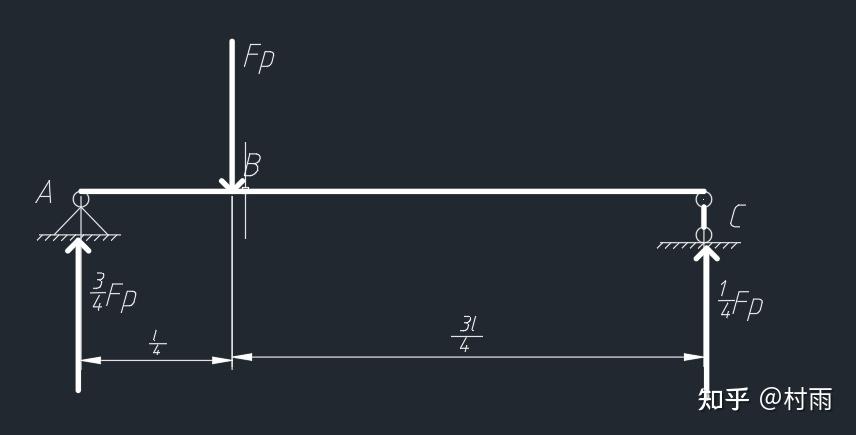
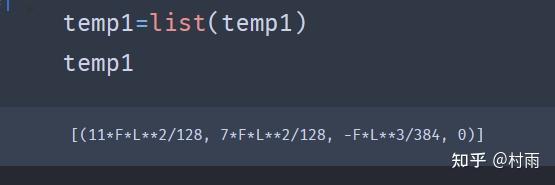
使用python_sympy库解决材料力学问题 (2) 今天下午本想好好写写材料力学,学到梁的挠曲线近似微分方程这一节,解方程、联立方程组求解写得我吐血,于是我就想着用sympy来解决,话不多说,先看题 题: 简支梁受力如图所示,











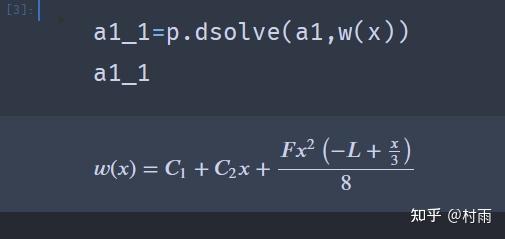
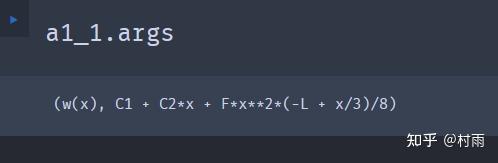
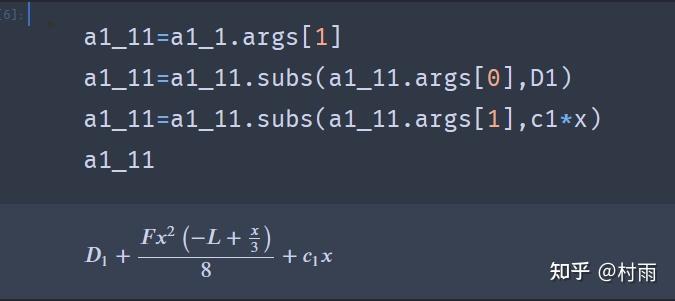
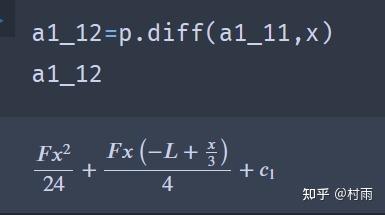
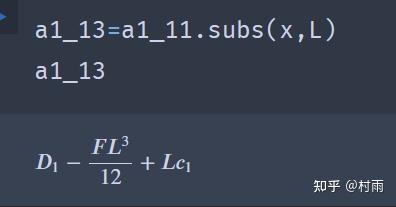
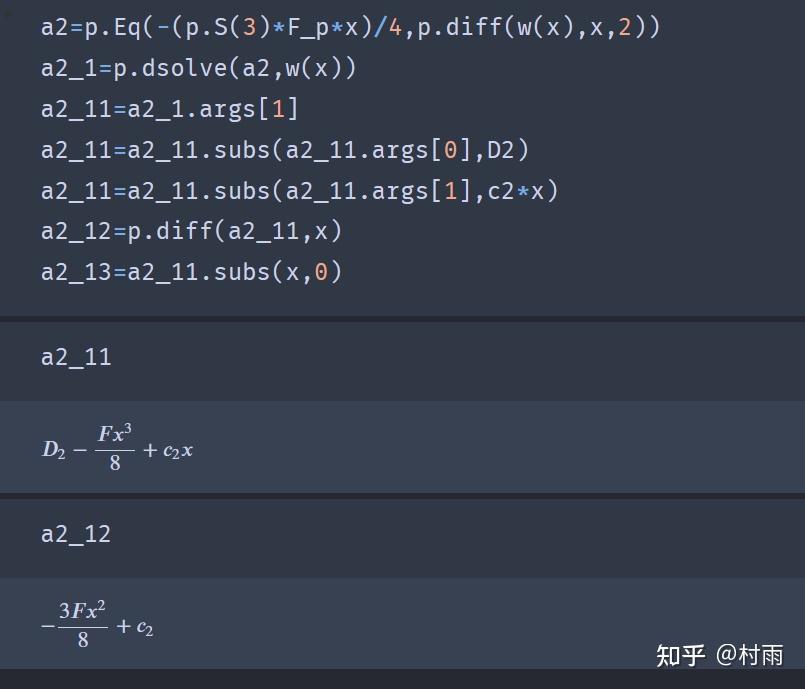
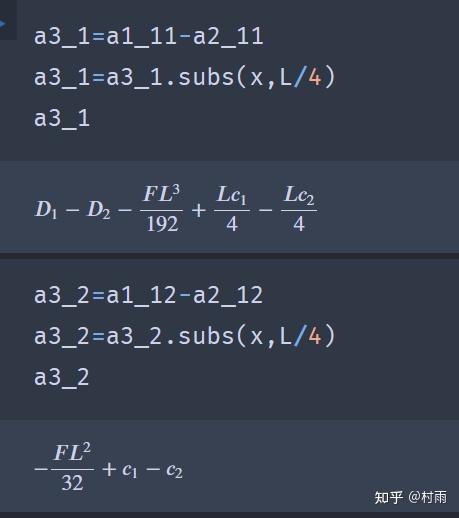
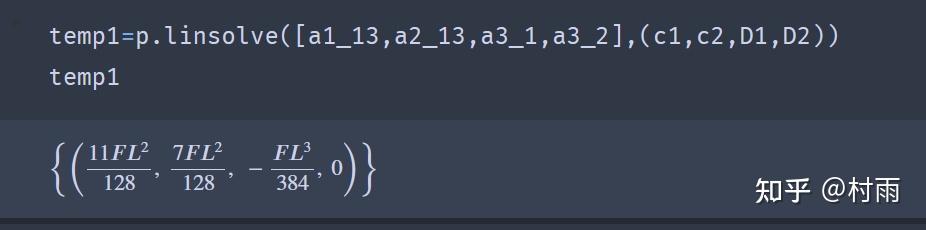
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/36094.html