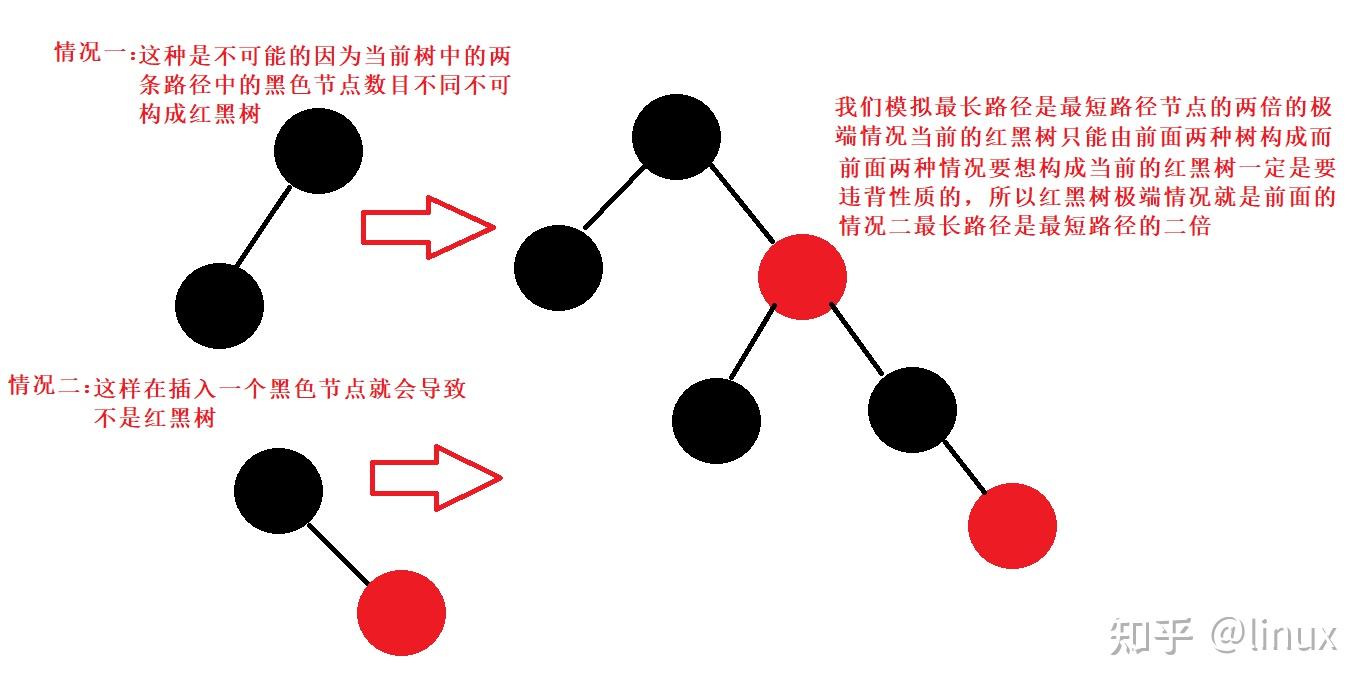
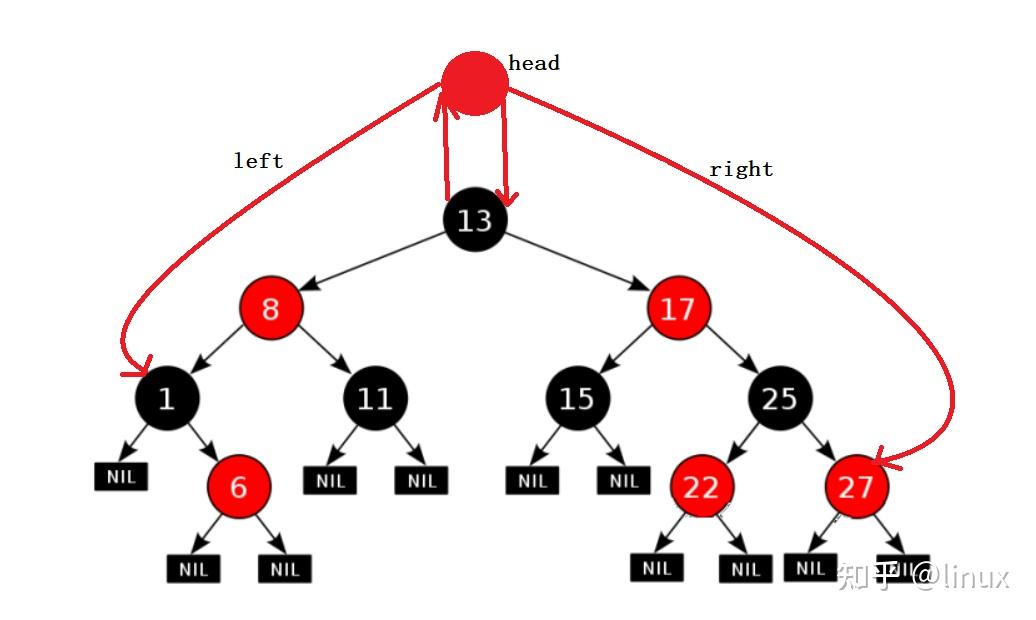
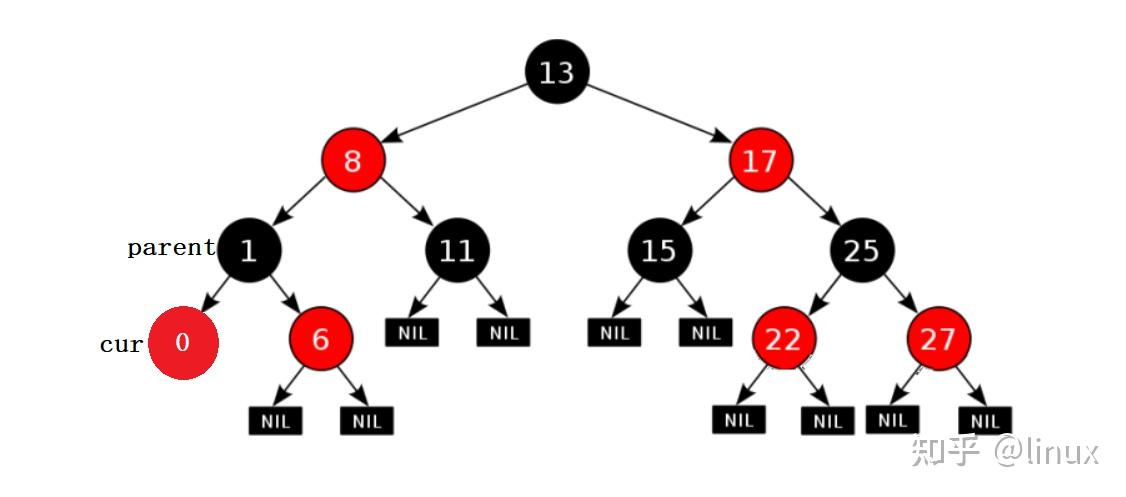
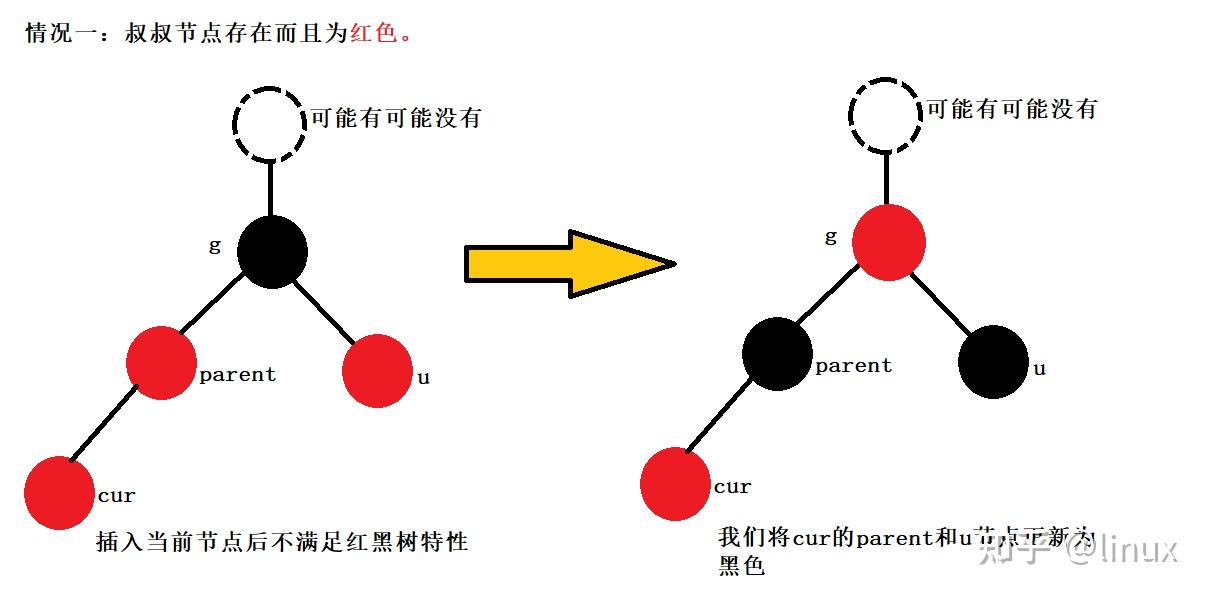
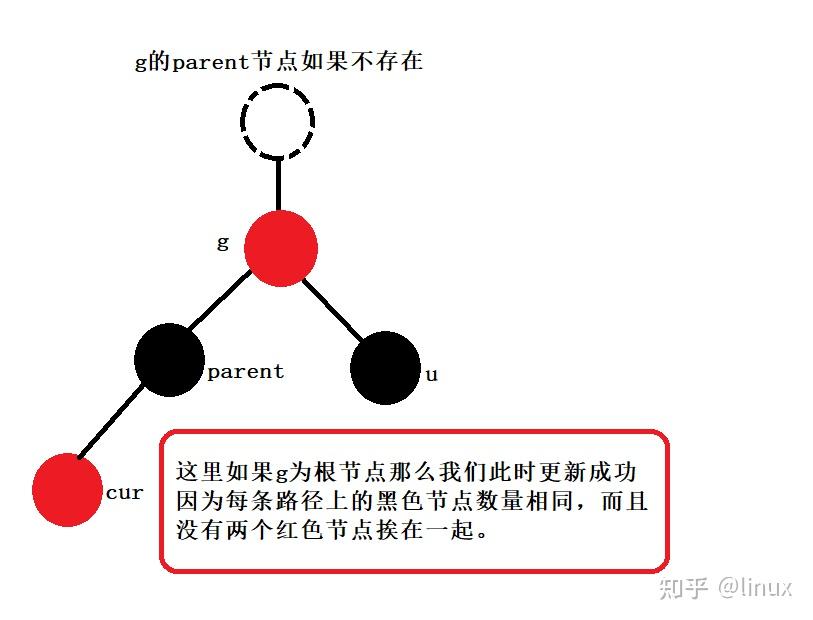
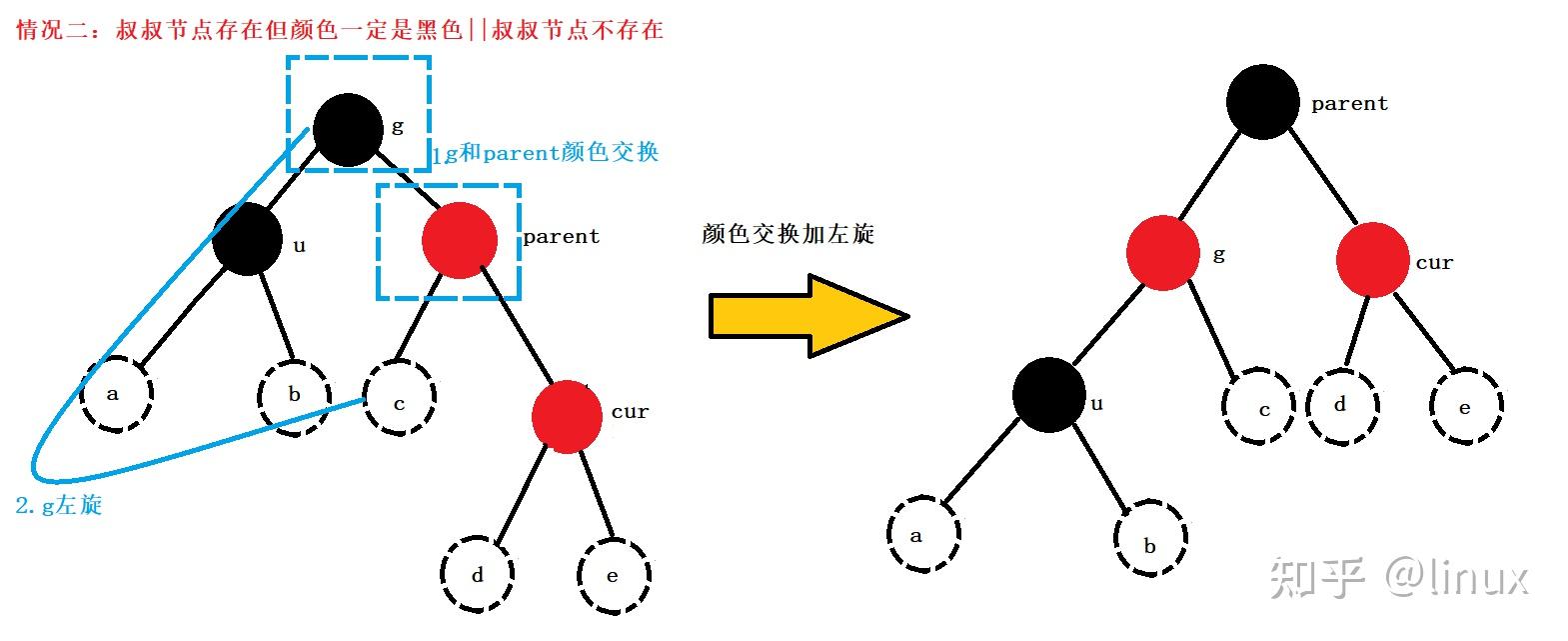
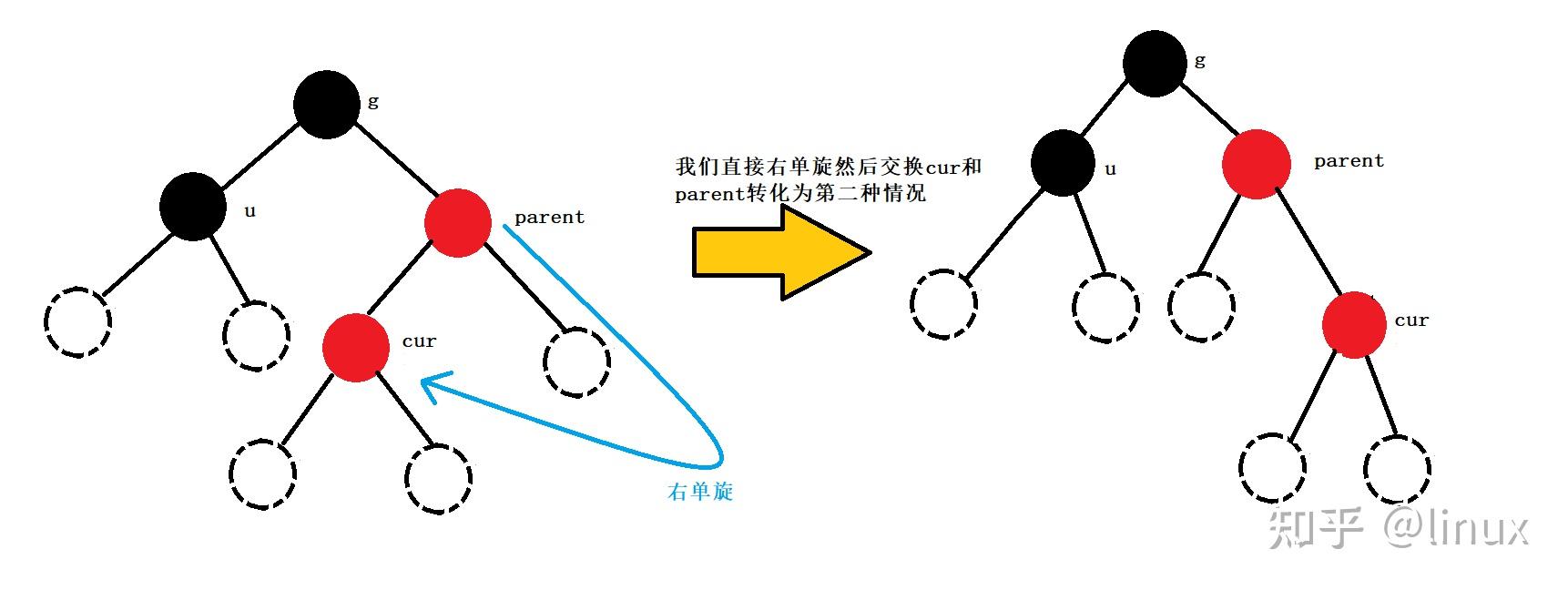
用通俗的语言解释一下红黑树有什么用处? 高中生,学习编程.最近正在拜读算法界的Bible<算法导论>,读到关于红黑树的介绍时基本理解了其概念,但是依然不清楚红黑树在算法中具体的作用.希望各位神犇能用通俗的语言帮我解释一下红黑树的用处.谢谢! 1. 红黑树的概念 红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。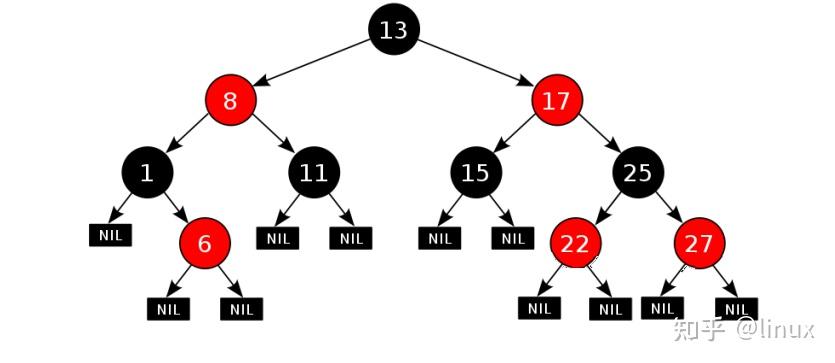
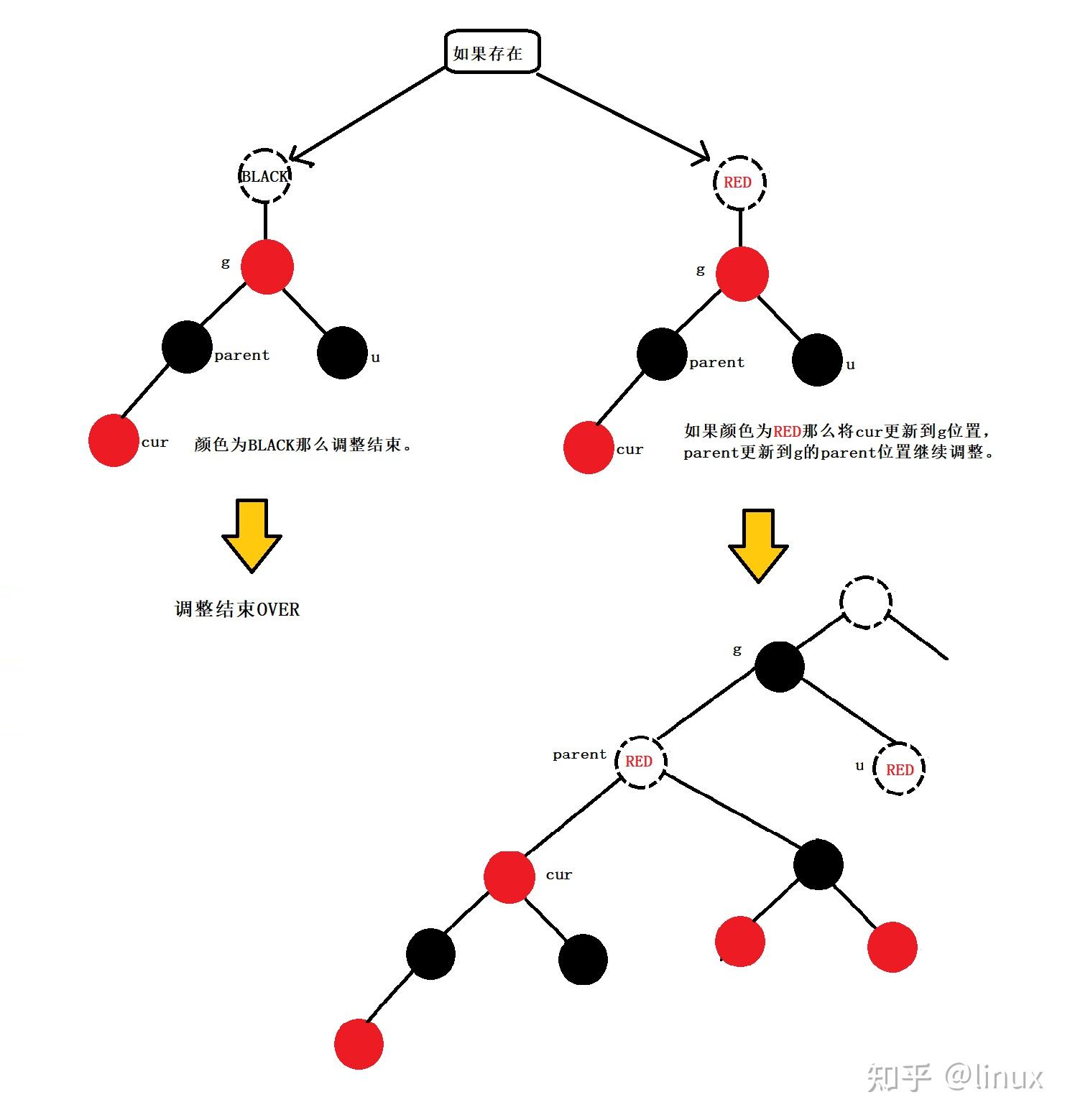
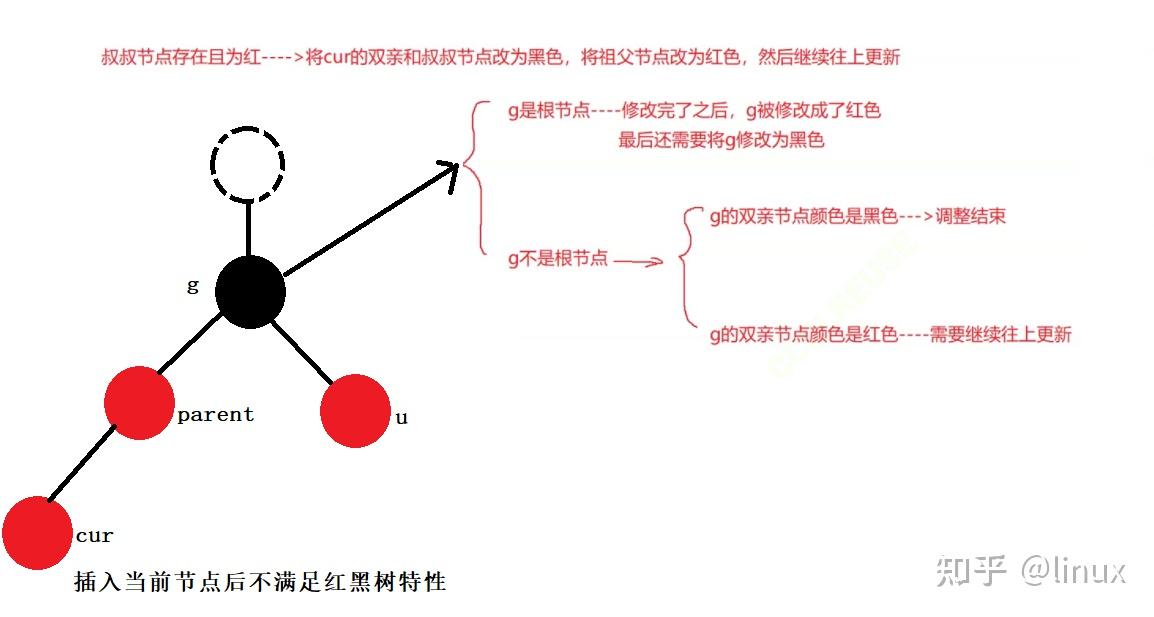
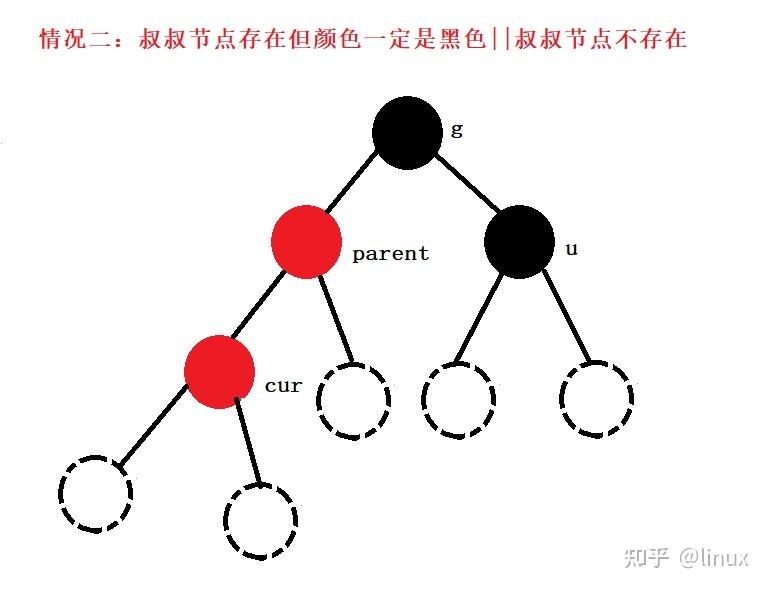
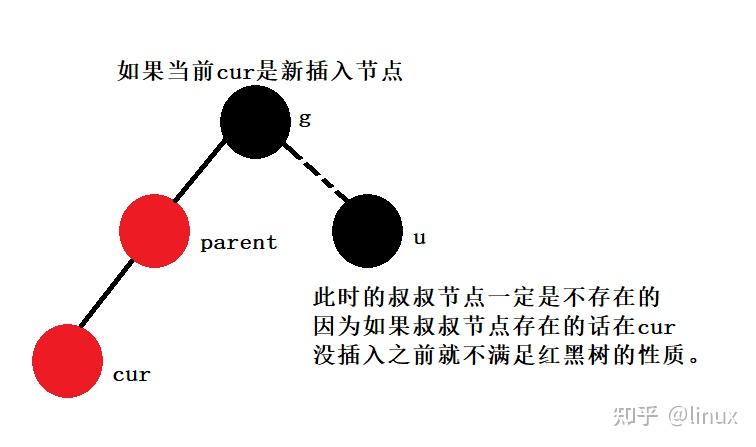
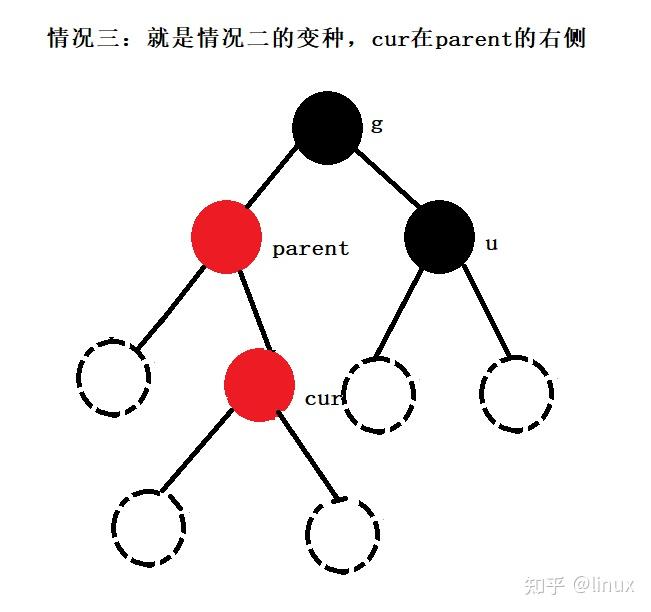
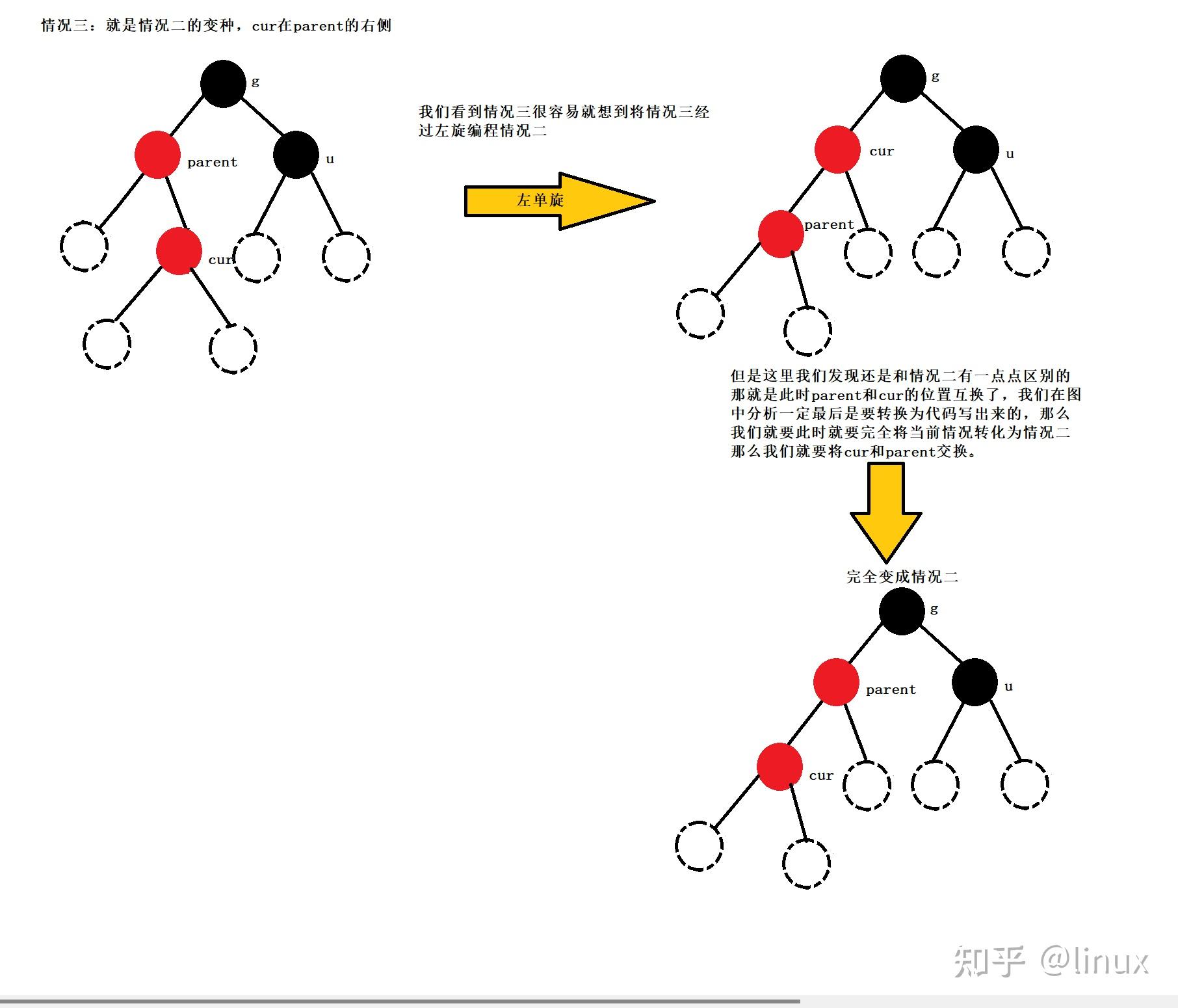
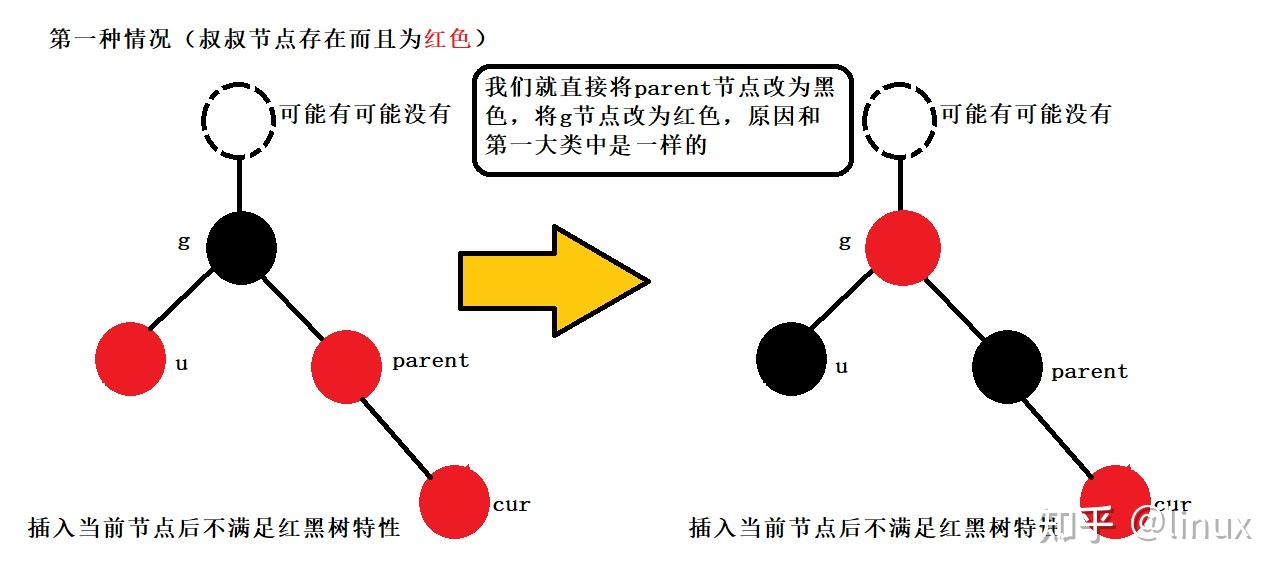
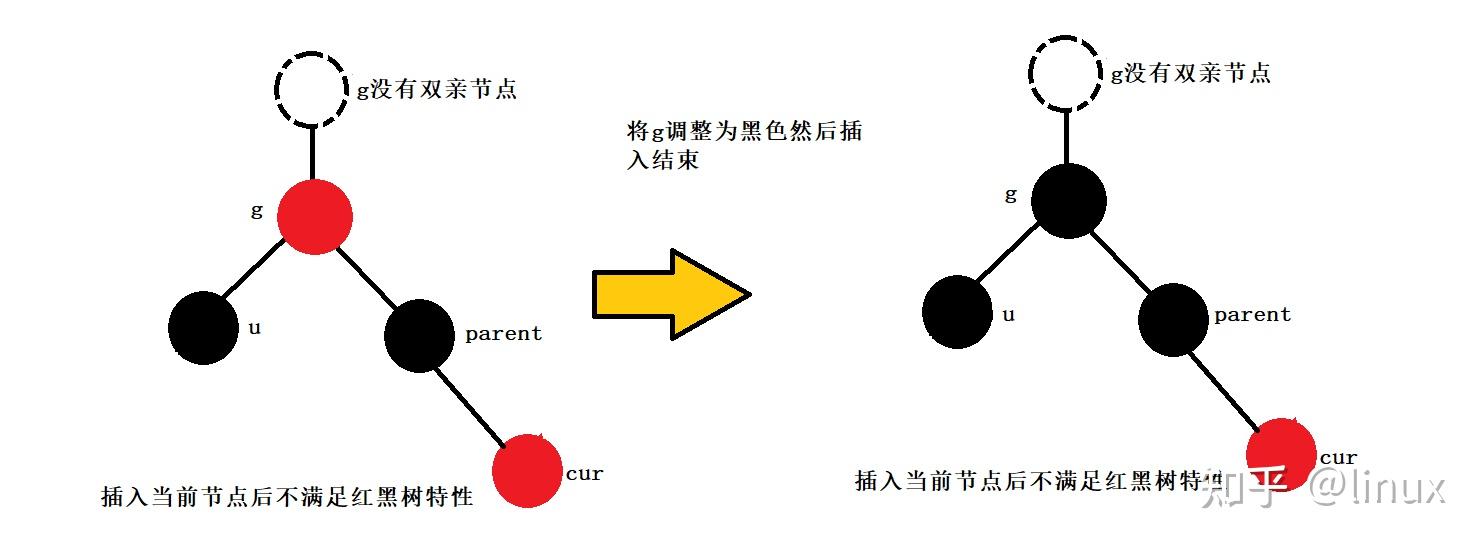
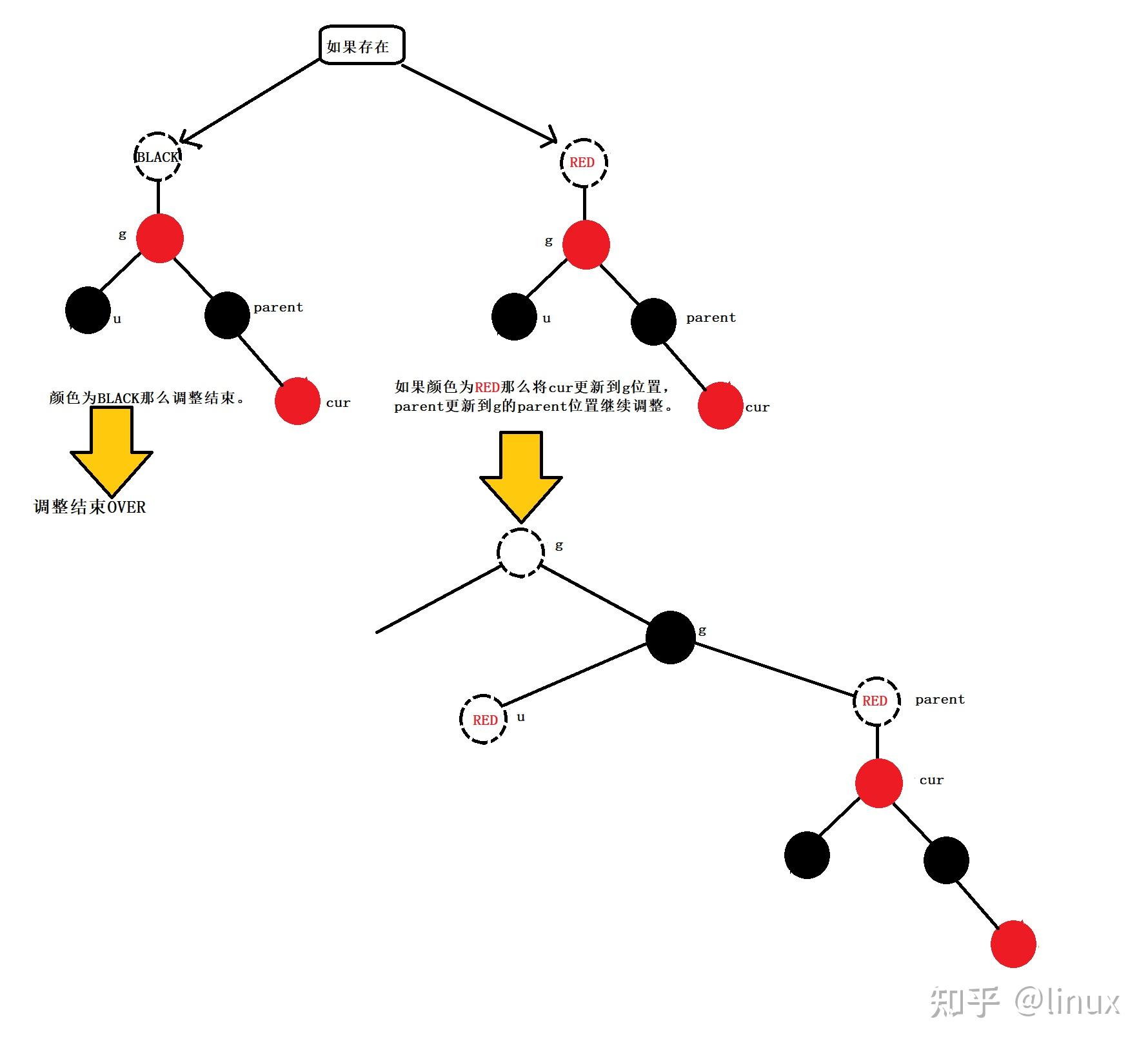
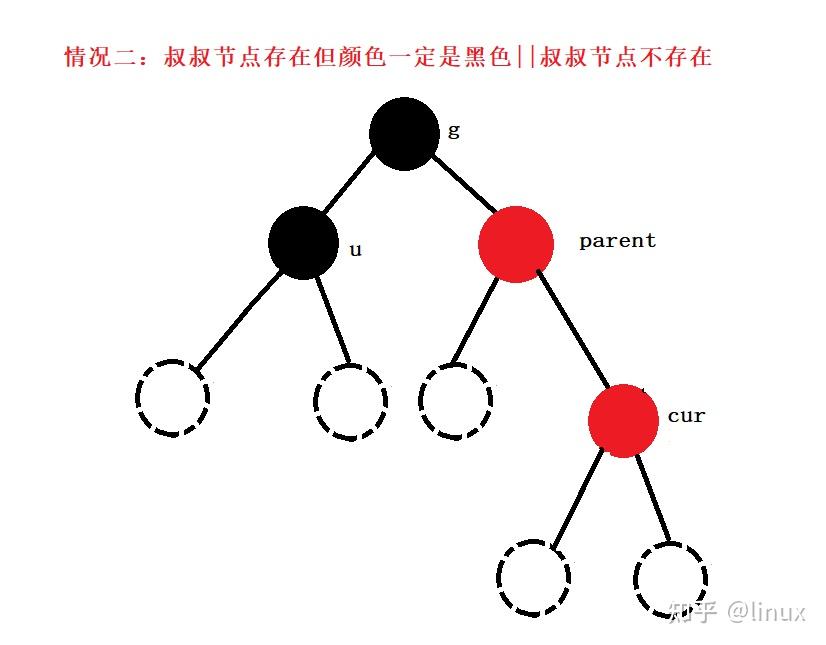
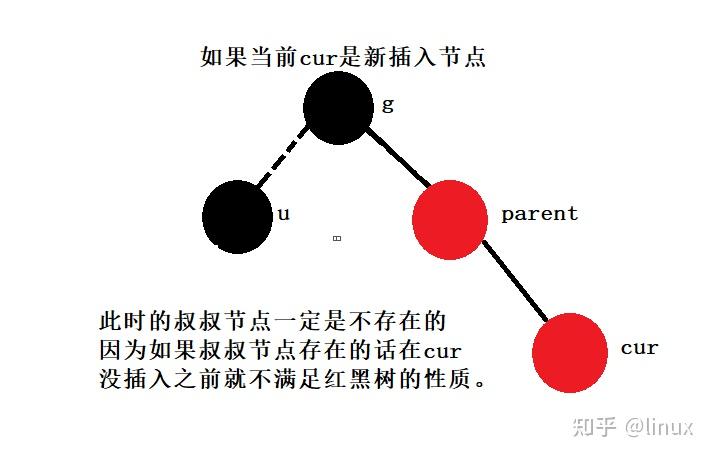
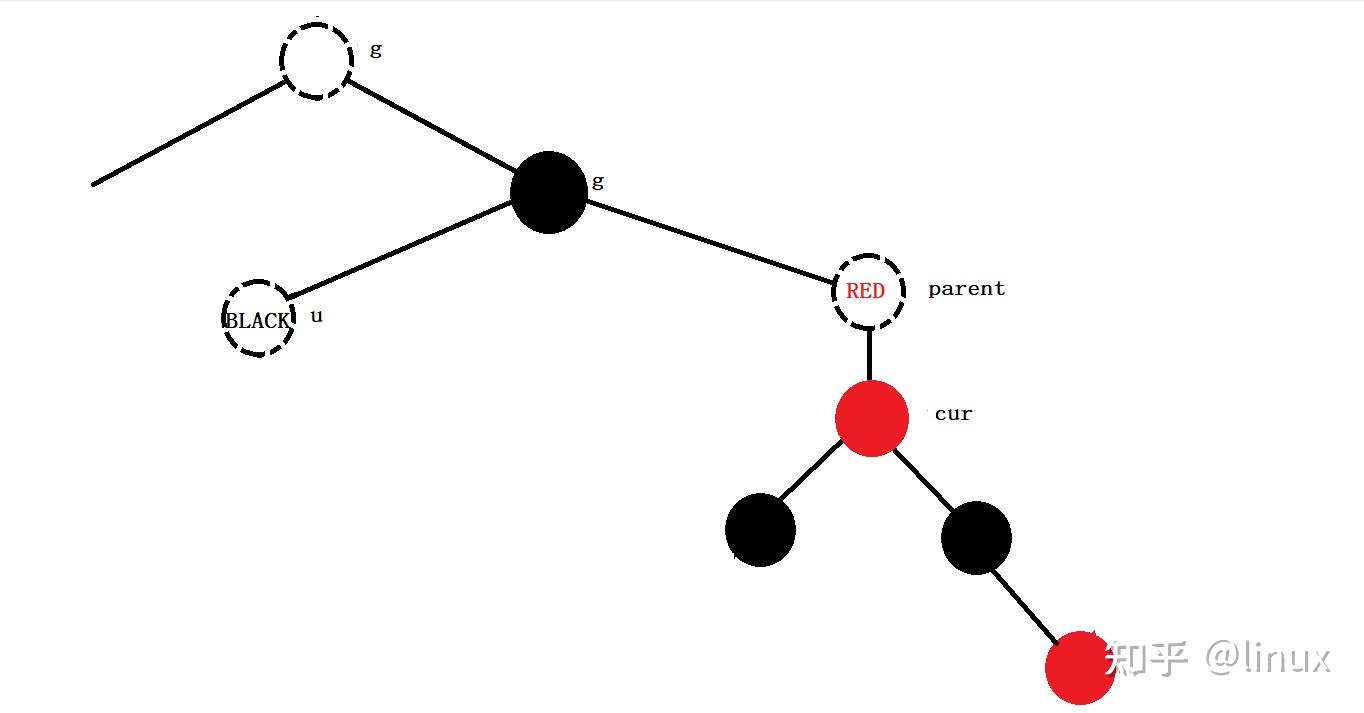
2. 红黑树的性质 2.1. 每个结点不是红色就是黑色 2.2. 根节点是黑色的 2.3. 如果一个节点是红色的，则它的两个孩子结点是黑色的（不会出现连在一起的红色节点） 2.4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点（在计算一条路径中黑色节点个数的时候要带上叶子节点，因为叶子节点也是黑色的，也就是空节点）。 2.5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)（为了保证空树也是红黑树） 2.6.红黑树确保没有一条路径会比其他路径长出俩倍（红黑树前面的性质保证了当前的性质）
3. 红黑树的实现 3.1. 带头节点的红黑树 这里我们将红黑树的实现给为带头的红黑树，因为红黑树是map和set的底层数据结构这里我们实现出来红黑树就可以直接用当前我们实现的带头红黑树来实现map和set至于头节点的给出是为了方便于map和set的遍历，在STL中我们区间给出都是左闭右开区间的，既然红黑树作为map和set的底层数据结构那么我们就一定有位置要来放map和set的迭代器，那么就可以将begin位置的迭代器放在head的左，end位置的迭代器可以放在head位置。这里我们将红黑树头节点的颜色给为红色。
3.2. 红黑树的节点
3.3. 红黑树插入节点的分析（实现红黑树最最最关键的一步） 可以看到我们上面在红黑树节点的构造的时候将节点的默认颜色给为红色，那么我们在插入节点的时候就要特别考虑性质3：不可以有两个红色节点连在一起。这里我们可以一共可以分为两大类，一类将节点插入当前红黑树的左子树中，另一类就是将节点插入红黑树的右子树当中。 第一大类（将节点插入红黑树的左子树中） 第一种情况（叔叔节点存在而且为红色，这里将节点插入红黑树的内测还是内测处理方式是一样的） 1.我们插入节点的parent节点为黑色：那么这种情况是不需要调整的。
2.我们插入节点的parent节点为红色，而且插入节点的叔叔节点也存在而且为红色的，那么当前节点插入之后就违反了红黑树的性质3，就需要对当前树进行调整。这里解决的时候我们就将当前parent节点和叔叔节点u的颜色变为黑色。
为什么要这样做呢？ 答案：这里我们将cur节点插入之后要解决当前parent和cur颜色都为红色的问题，那么只能将cur和parnet其中一个节点的颜色变为黑色，但是肯定不能将cur节点变为黑色，因为这样在包含cur的路径中就多一个黑色节点，那么我们就要将除包含cur之外的路径中的黑色节点全部都减少一个，又因为此时cur是新插入的节点如果将cur颜色变为黑色那么此时就只有一条路径黑色节点个数+1，如果要调整的话，其他所有节点中黑色节点个数都要减少一个这样肯定是不行的，那么我们只能将parent节点的颜色变为黑色，那么当parent节点变为黑色之后我们可以看到在包含parent的路径中黑色节点增加，但是包含parent节点的路径一定包含parent的双亲节点也就是g节点那么我们将双亲节点g颜色改为红色，那么不就将包含parent路径的黑色节点个数减少一个了吗。然后我们发现又出现新的问题了，就是原本包含u节点的路径因为g节点变为了红色那么包含u节点的路径中少了一个黑色节点（因为包含u节点的路径一定包含g节点）那么我们此时只要将u节点的颜色变为黑色即可。 上面将parent和u的节点更新为红色之后，我们还要考虑g节点让我们更新为红色之后那它的双亲节点是否存在，是否是红色节点： 相关视频推荐 5种红黑树的场景，从Linux内核谈到Nginx源码，听完醍醐灌顶 5种红黑树的用途，从应用到内核场景的优缺点 学习地址：c/c++ linux服务器开发/后台架构师 需要C/C++ Linux服务器架构师学习资料加qun（资料包括C/C++，Linux，golang技术，Nginx，ZeroMQ，MySQL，Redis，fastdfs，MongoDB，ZK，流媒体，CDN，P2P，K8S，Docker，TCP/IP，协程，DPDK，ffmpeg等），免费分享
如果g的双亲不存在： 那么此时g就是根节点那么我们此时需要将g颜色更新为黑色，因为红黑树的根节点必须是黑色的。
如果g的双亲存在： 分为两种情况：1、g的双亲为黑色那么调整结束直接退出。2、如果g的双亲为红色（而且g的叔叔为红色，这里如果g的叔叔为黑色我们下面会讨论）那么我们更新cur和parent继续当前的调整过程。
我们可以总结一下我们的第一种情况：
第二种情况（叔叔节点存在而且一定为黑色或者叔叔节点不存在）
当前cur节点是新插入节点，那么叔叔节点一定是不存在的
当前cur不是新插入节点，那么就和我们第一种情况，我们更新完祖父节点后祖父节点还有叔叔节点的情况这时叔叔节点一定是黑色的，其实下面这种情况的出现就是为了解决上面第一种情况：更新完祖父节点之后祖父节点还有叔叔节点且叔叔节点为黑色。
那么我们如何解决当前场景呢？ 我们这里一共给出三步： 1.将parent节点改为黑色 2.将g节点改为红色 3.将g节点右单旋
当叔叔节点不存在也是一样的做法
我们总结一下第二种情况：第二种情况其实就是对第一种情况其中的一种情况的分析解决。
第三种情况：第三种情况其实就是对第二种情况的变种，cur在parent的右侧。
如果你可以坚持看到这里，恭喜你你已经理解了手撕红黑树中基本最难的地方了，马上就能撕碎红黑树！！！
情况三的解决方案：（其实情况三就是转化为情况二来解决的） 至此我们就将红黑树插入的第一大类看完了，接下来就是第二大类基本就和我们的第一大类一样，不同的地方就是第二大类将节点插入到红黑树的右子树。 第二大类（将节点插入红黑树的右子树中） 第一种情况：插入节点的parent节点为红色而且叔叔节点存在为红色（这里将节点插入红黑树的内测还是内测处理方式是一样的）
那么我们和第一类中一样也分为g有双亲节点（g的叔叔为红色，g的叔叔为黑色两种情况）和没有双亲节点。 g没有双亲节点：没有双亲节点我们将g颜色更新为红色直接返回即可。
g的双亲节点如果存在:那么我们就又分为两种情况一种是双亲节点为黑色节点那么调整结束满足红黑树性质，另一种双亲节点为红色那么，就又分为两种情况：一种是当前叔叔节点为红色那么我们重复当前的调整步骤，另一种就是我们下面情况二要讨论的叔叔节点为黑色。
第二情况：叔叔节点存在但颜色一定是黑色||叔叔节点不存在
如果叔叔节点u为黑色节点当前节点一定不是新插入节点。
那么就是我们遗留的第一种情况中未处理的情况就是下面这种情况：
由于与第一大类中第二种情况类似我们这里直接将解决方式给出，这里的叔叔节点不存在也是同样的做法
第三种情况：叔叔节点存在但颜色一定是黑色||将节点插入内侧
4. 红黑树模拟实现 看到这里恭喜你，你已经彻底掌握了红黑树的插入，接下来你可以动手试一下红黑树的模拟实现，这里我也给出红黑树的模拟实现代码可以作为参考。 5. 基于红黑树的map的模拟实现 6. 基于红黑树的set的模拟实现
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/26284.html
