matlab fft频谱图_matlab fft频谱图 两个信号的幅值差

为什么FFT变换后的幅值感觉不对？ 请看一下问题出在哪里（matlab环境）。
　　原始信号的幅值最大值都在40+ 50+ 为什么经过fft之后的幅值却只有9.9 我已把fft的结果通过*2/nfft 得到真正的幅值. 这是我的代码 感觉应该没错，但这结果很难想明白， 感觉fft后的结果 的幅值应该也在40+50+的样子，可得到这样的结果这是为什么？time = [1:1:2049255];current = four(1,:); % datadata= (current/220)*1000;dt = (time(2)-time(1))*60; % the interval between samplefs = 1/dt; % after FFT, the max limitax = (abs(fft(data,length(time)))*2)/length(time); f = (1:length(time))*fs/length(time); %% % figuresubplot(211);plot(time,data);xlabel('Time(min)');ylabel('Power(mA)');title('Power signal profile');subplot(212);% plot(f,ax,'LineWidth',1);xlim([0 0.0083])semilogx(f,ax);xlabel('Frequency(Hz)');ylabel('Power(mA)');title('Power VS Frequency');

　　matlab的fft以及不少信号处理教材上的fft是按照如下公式：

　　变换后能量是会扩大的。若要能量不变，公式为：

　　代码为：

　　—————–

　　Last but not least，功率谱不能这么简单粗暴的估计。FFT有截断效应，相当于把要分析的信号乘以一个矩形窗，频域相当于于一个sinc函数卷积，使真实频谱发生扩散。所以至少要加一个窗函数，再用幅度谱的平方估计功率谱。

　　觉得麻烦就用pwelch(x)吧。

　　你这里所说的真实的幅值应该理解成某个频点下的幅值大小，这可以根据DFT公式看出来。

　　但是这个值等于等效到该频点上的对应幅值，根据帕斯瓦尔定理这个值应该是 才对，利用这个值计算，能量才相等。这两个概念并不一样。后者就是高票答案说的那个东西。

　　另外还有个问题，楼主你的Ts并不是1，所以你对离散傅里叶采样的结果应该用 量化才对。好像更小了（逃跑）。

　　真的naiive，原来楼主才是对的呀

　　 DFT虽然好，但由于计算的次数太多，数据量一大就显得相当复杂

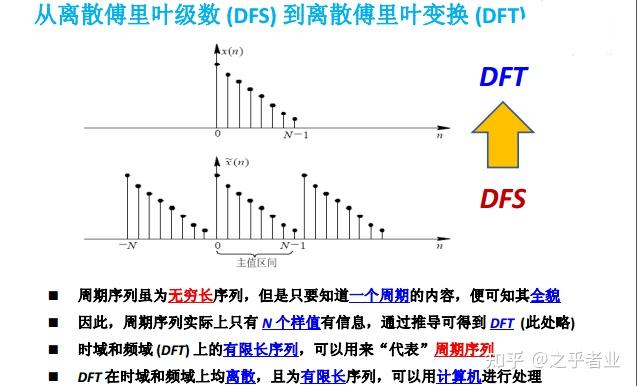
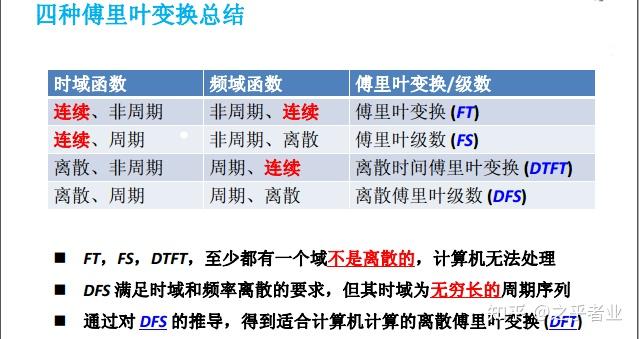
　　最后将DFT进行改进成FFT，即FFT是DFT的快速算法，本质上仍然是DFT。

　　MATLAB中提供“fft”函数，可以直接对数据进行快速傅里叶变换。但是由于FFT的本质仍然是DFT，则得到的频谱是用功率谱密度（PSD）定义的，也就是它的幅值表示的是单位带宽的幅值。

　　N：样本点

　　 ：采样频率

　　FFT变换之后的横轴为频率轴，频谱图横坐标显示的最大频率点为 （奈奎斯特采样定理），频率的坐标间隔（频率分辨率）为 ，也就是说最小能分辨的两个频率之间的差值要大于 。

　　横轴的频率点为：（0：1 ： ）。（经过FFT之后，频谱是关于中间位置对称的，只需要观察0~ 即可）

　　对于实数信号而言，N（先假设N为偶数，其实最好的情况是为2的n次幂个）个离散点的DFT将产生 +1个频率点（因为无论怎样都会有0频率），频率的序号从0~ 。故而N个实数点经过DFT之后的频谱带宽为 ，每一个频率点所占的带宽为 ，所以经过FFT之后的频率对应的幅值并不是真实的幅值，想要将FFT之后的频谱图跟实际的幅值对应，就要进行相应的转换。

　　那么，重点来了，怎么转化呢？

　　上边我们说的就是每一个频率点所占的带宽是 ，将带宽跟FFT之后得到的幅值相乘即可对应到原本的幅值。但是，需要特别注意的一点：

　　频率序号为0和 的两个点的带宽只占中间频率点的一半，也就是占 的带宽，因此只需要将幅值乘以 即可。

　　到这，也许有细心的童鞋发现了， 这个数据对应的N为偶数是最好的，那如果恰好N为奇数又该怎么解决呢？

　　事实上，当我们的样本点N为奇数时，只有0频率占 带宽，其余的 个频率点仍然是对应幅值乘以 得到真实的幅值。

　　以上都是基于实数信号，对于复数信号而言（生活中大部分的模拟信号转化为数字信号都是实数信号，很少遇到复数信号），处理方法则相对简单多了。对于复数信号，N个点FFT之后会产生N个频率点，频谱的带宽为N，每个点所占的带宽为 ，将每个幅值都乘以 即可得到真实的频率幅值。

　　以下为MATLAB实操：以这个题目为例

　　1、不进行幅值修正的情况：

　　时域信号傅里叶变换之后的频谱图

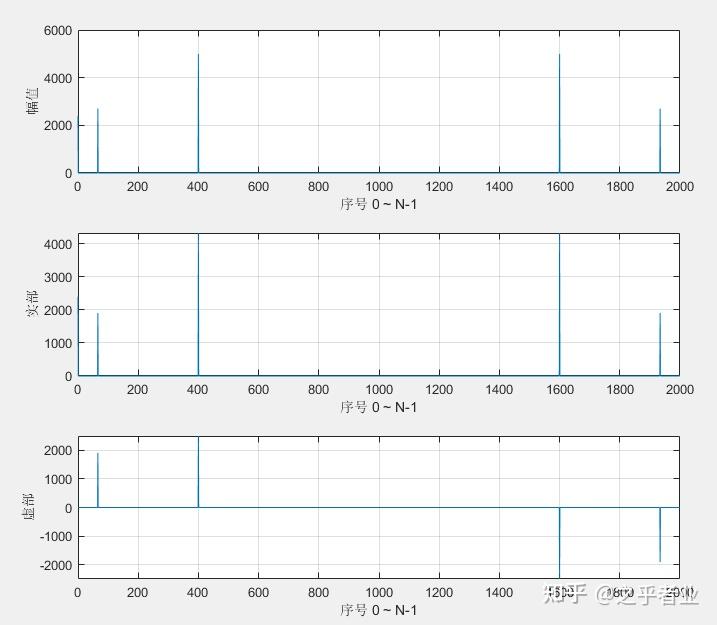
　　可以看到无论是幅值还是频率，跟我们所给的时域信号是对应不上的，并且同样也证实了关于中心点对称的观点，因此我们接下来只需观察从0到N/2的频率点即可。

　　2、对幅值进行修正的情况：

　　不用担心相位图杂乱无章，在没有频率处的相位是没有意义的，我们只需要有幅值处的相位即可

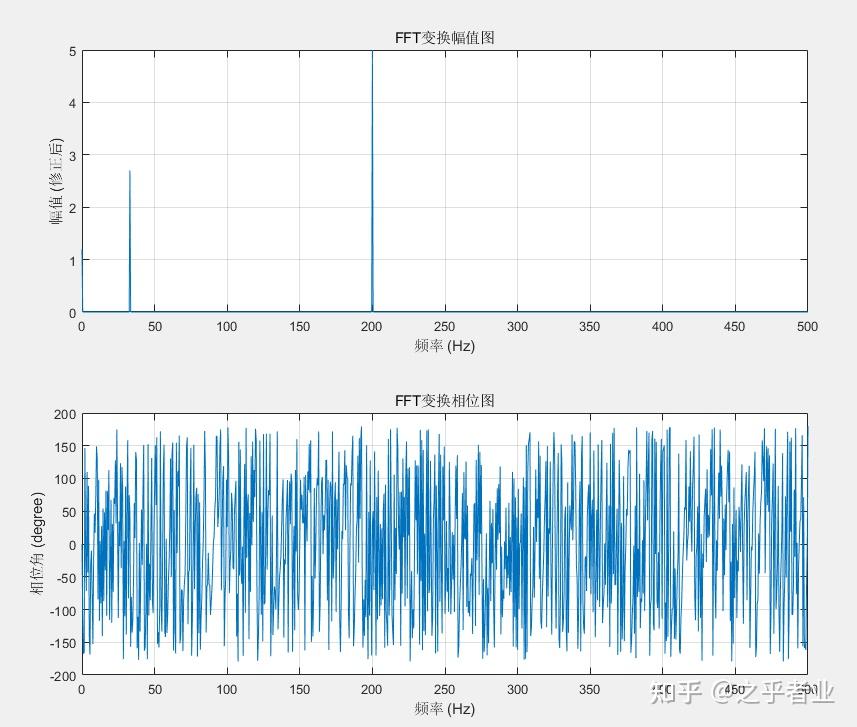
　　将图放大可以看到，修正后的幅频图跟时域对应相当好。

　　过程中如有任何问题，欢迎各位大佬在评论区讨论以及指出错误。

　　有意向代码，请转文末观看代码方式~也可转原文链接~

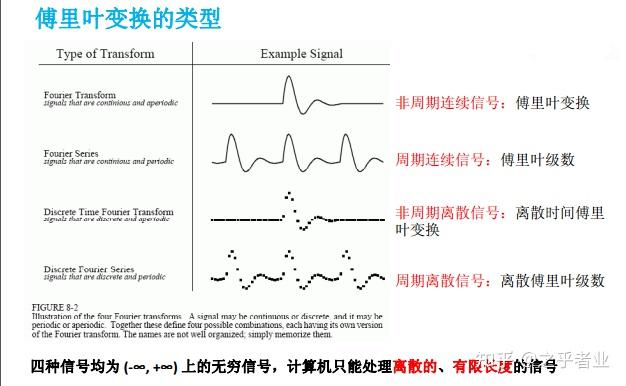
　　1 基本定义

　　EEMD+FFT+HHT组合算法的原理是：

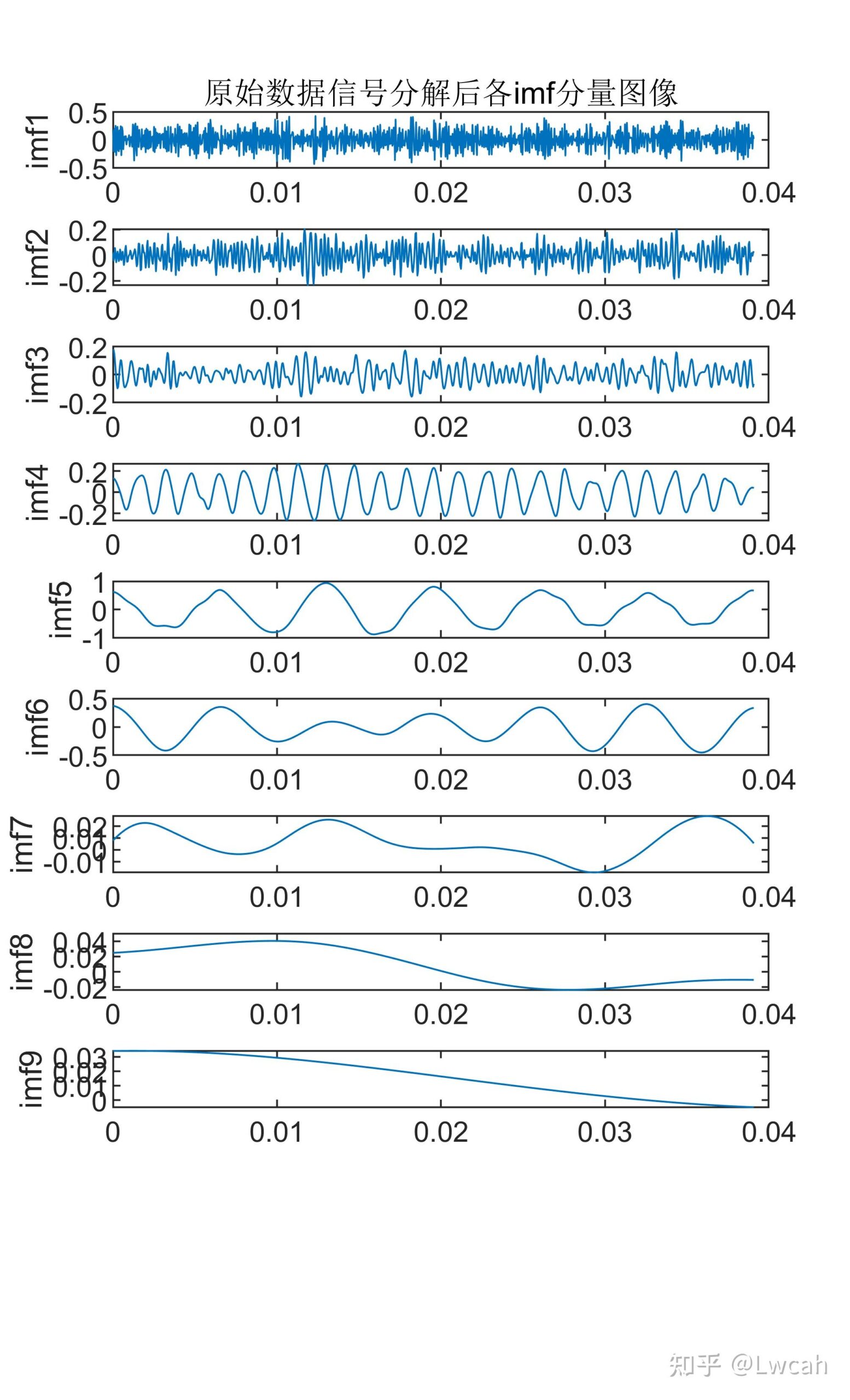
　　首先，利用EEMD（集成经验模态分解）对信号进行分解，得到一系列的IMF（固有模态函数）和一个残余分量。这些IMF代表了信号中的各种频率成分，每个IMF都包含了信号中的一部分信息。

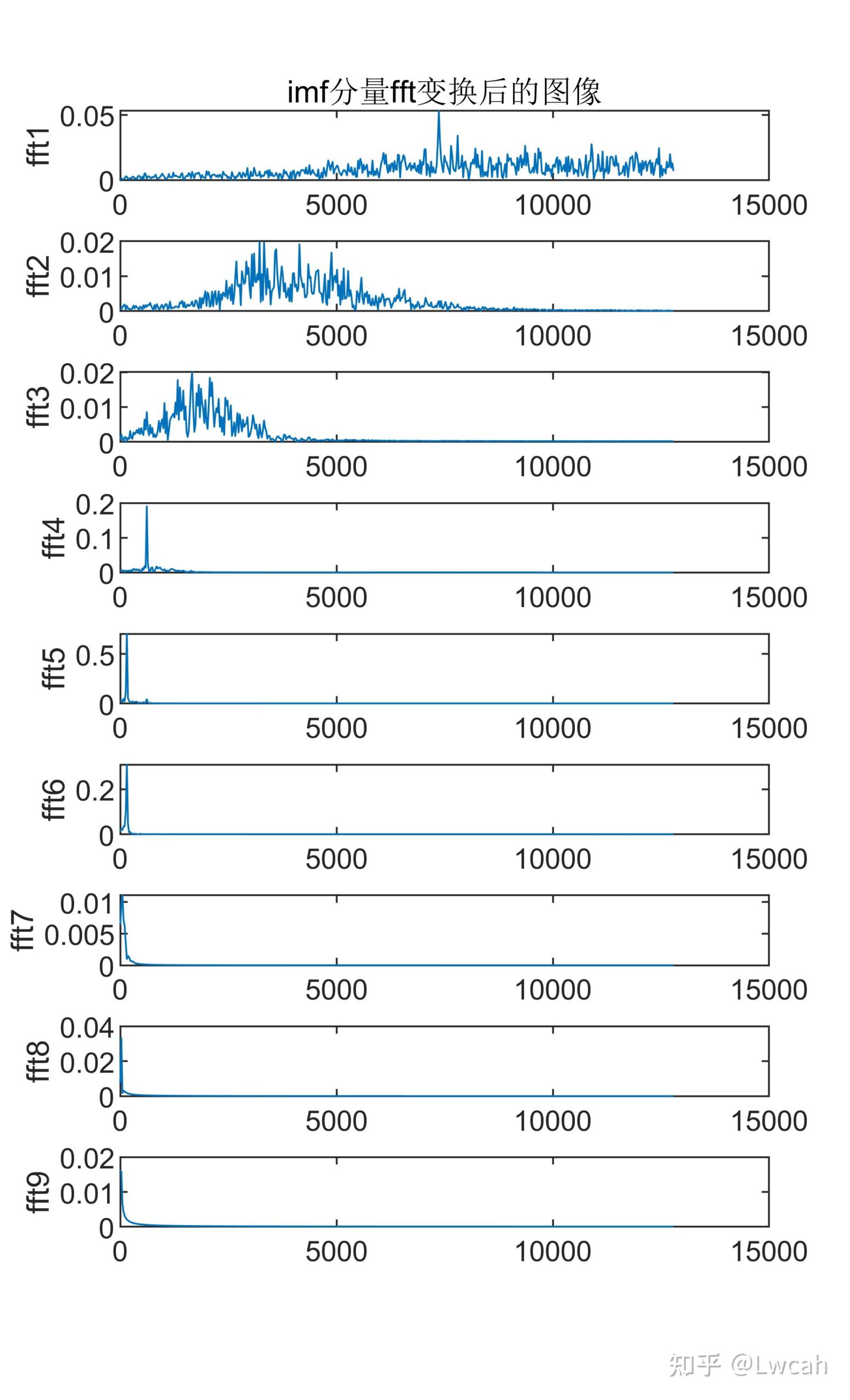
　　然后，对每个IMF进行FFT（快速傅里叶变换）计算，得到其频谱信息。FFT是一种高效计算离散傅里叶变换及其逆变换的方法，可以快速地计算出信号的频谱。通过FFT，我们可以得到每个IMF在频率域中的表示。

　　最后，利用HHT（希尔伯特-黄变换）对每个IMF进行希尔伯特谱分析，得到每个IMF的时间和频率信息。HHT是一种新的信号分析方法，能够同时提供信号的时间和频率信息，适用于非线性和非平稳信号的分析。通过HHT，我们可以进一步揭示每个IMF的频率和时间分布特征。

　　通过这种组合算法，我们可以更全面地分析信号的特征，提取出有用的信息。需要注意的是，在实际应用中，EEMD、FFT 和 HHT 的具体算法可能存在一定的差异和优化，以适应不同的应用场景和数据特点。此外，这种组合算法也需要一定的计算资源和时间成本，需要根据实际情况进行选择和应用。

　　除了上述提到的优点，EEMD+FFT+HHT组合算法还具有以下特点：适用性广泛：EEMD、FFT和HHT都可以用于处理不同类型的信号，因此该组合算法可以适用于各种不同的领域，如机械故障诊断、医学影像分析、语音信号处理等。组合灵活性：EEMD、FFT和HHT可以灵活组合使用，根据具体应用场景和需求进行选择和优化。例如，可以在EEMD分解后对每个IMF分别进行FFT计算，也可以在FFT计算后对每个频率分量进行HHT分析。自适应性：EEMD和HHT都具有自适应性，可以自动适应信号的特点和处理需求。例如，EEMD可以根据信号的局部特征进行分解，HHT可以根据信号的非线性特征进行希尔伯特谱分析。降噪能力：EEMD可以将信号分解成一系列IMF和一个残余分量，其中IMF包含了信号中的频率成分，而残余分量则代表了信号中的噪声成分。通过去除残余分量，可以有效地去除信号中的噪声干扰。多尺度分析能力：HHT可以进行多尺度分析，即在不同尺度下对信号进行处理和分析。这有助于提取出信号在不同尺度下的特征和模式，适用于多尺度问题的处理和分析。

　　总之，EEMD+FFT+HHT组合算法是一种综合性的信号处理方法，具有广泛的适用性、组合灵活性、自适应性、降噪能力和多尺度分析能力等优点。它可以用于各种不同的领域和场景，如机械故障诊断、医学影像分析、语音信号处理等，为信号处理和分析提供了新的工具和方法。

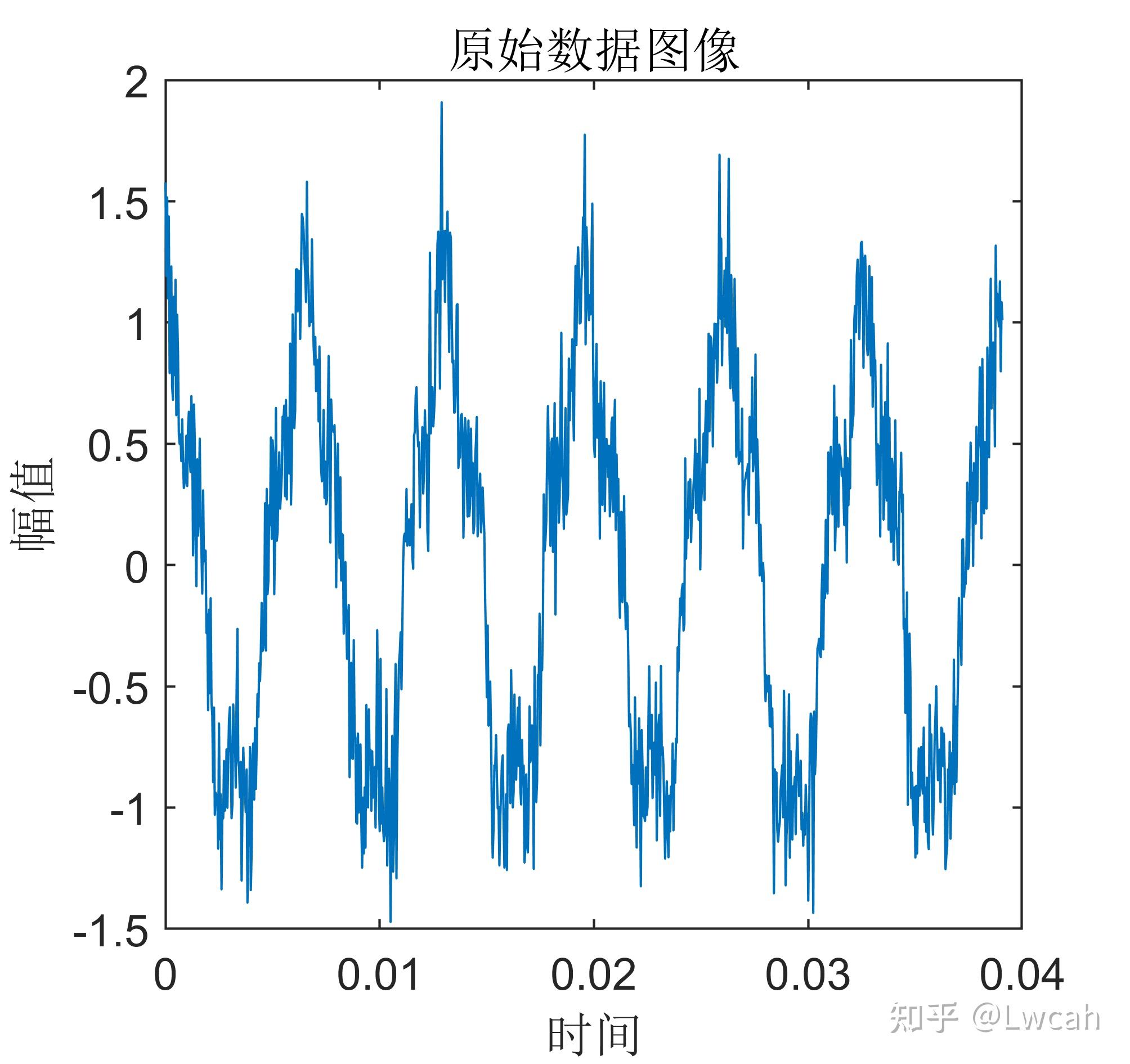
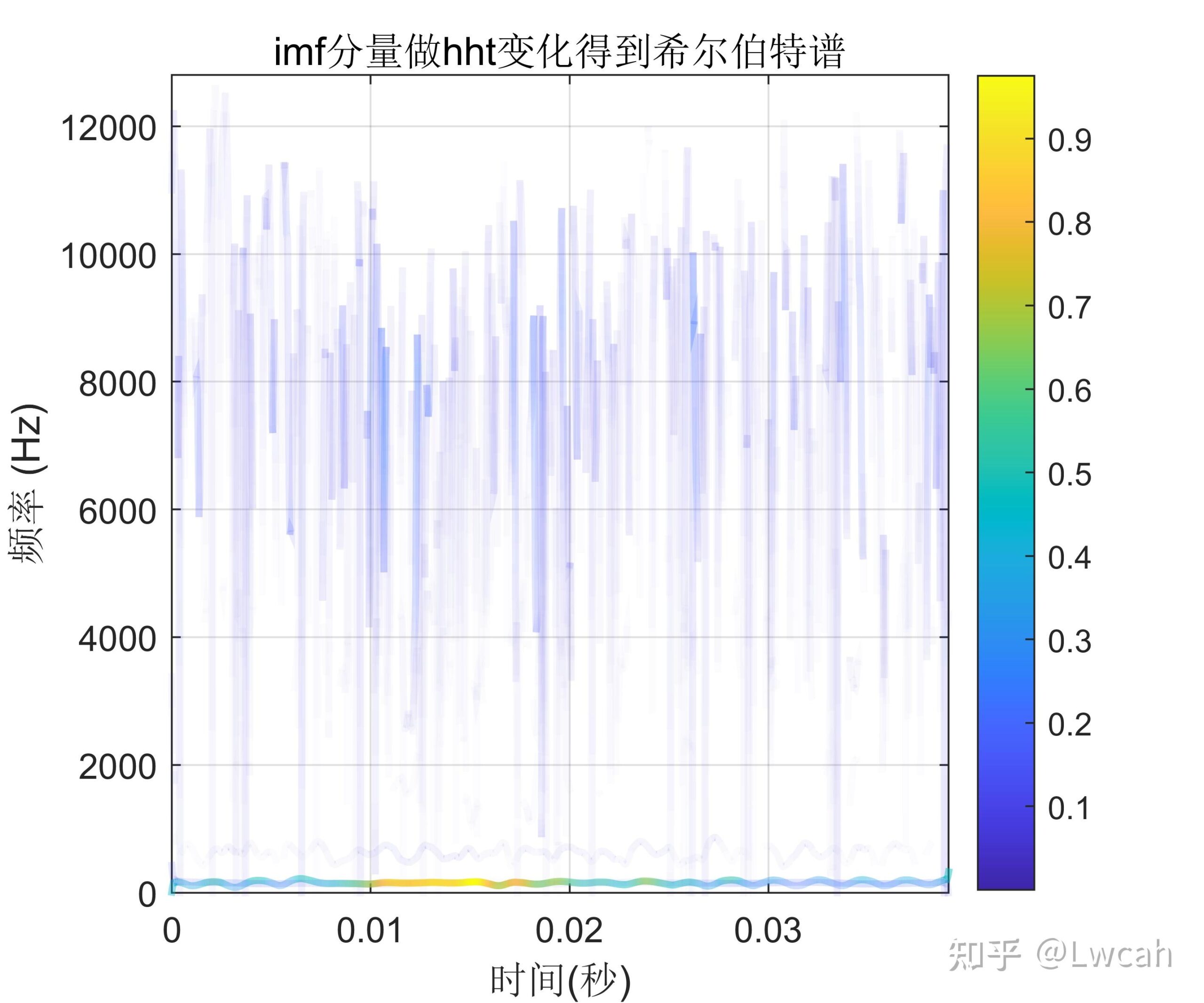
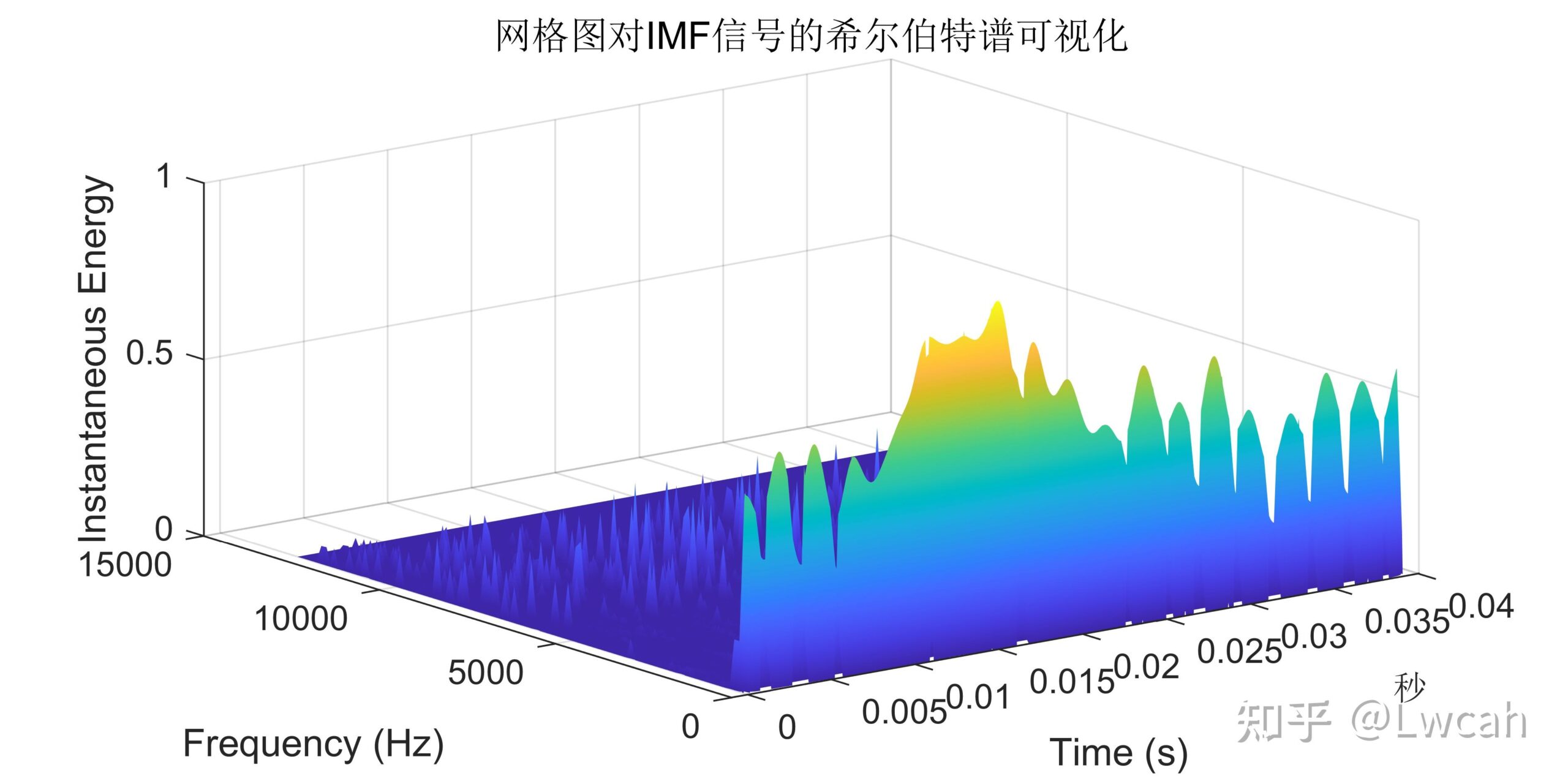
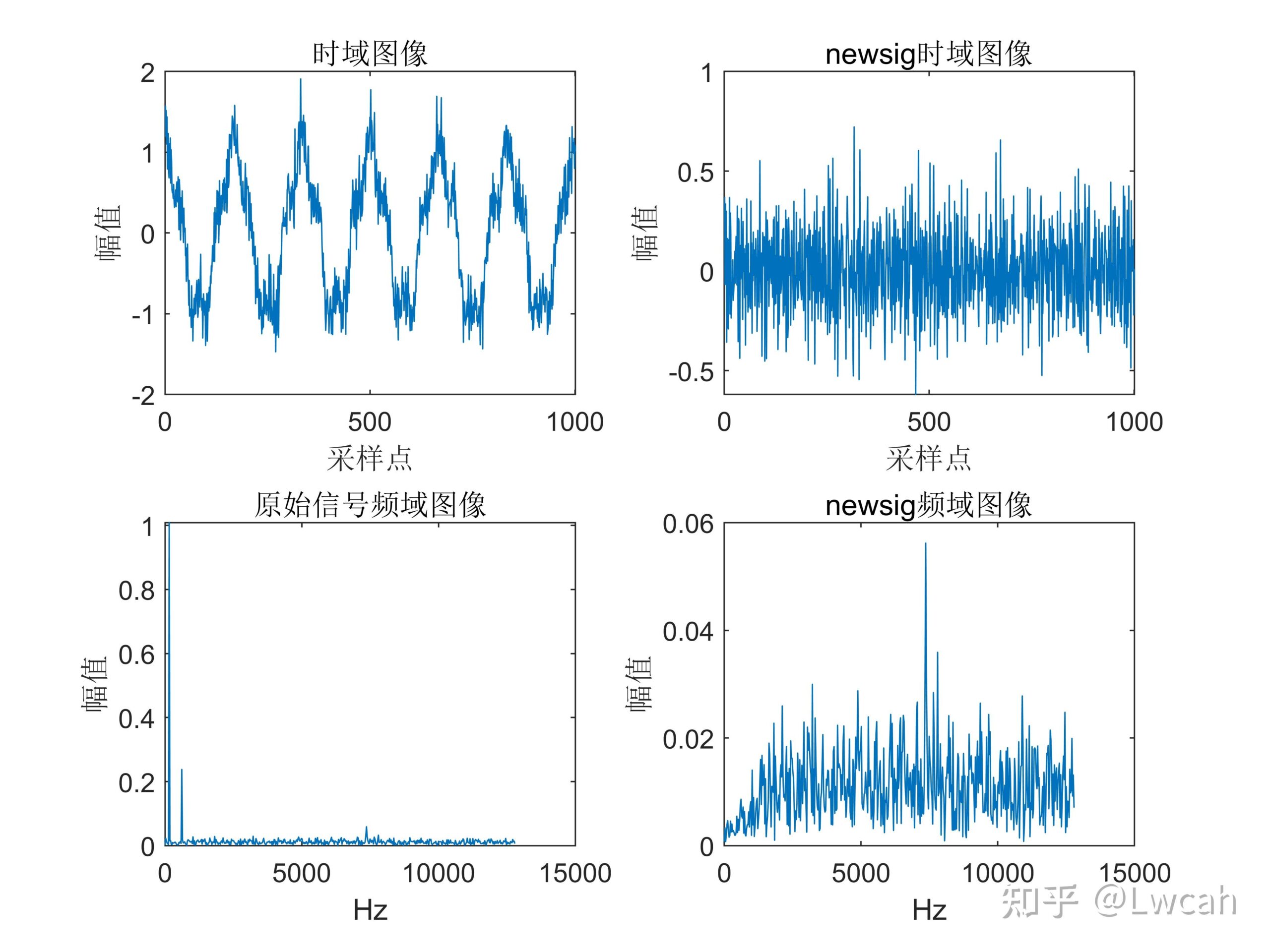
　　2 出图效果

　　附出图效果如下：

　　附视频教程操作：【MATLAB】EEMD+FFT+HHT组合算法_哔哩哔哩_bilibili

　　3 代码

　　MATLAB 开源算法及绘图代码合集汇总一览

　　https://www.aliyundrive.com/s/9GrH3tvMhKf

　　提取码: f0w7

　　参考了高赞 @知乎者业 的回答以及其他一些文章，自己写了一篇MATLAB和Python处理FFT数据的文章，供参考。

　　快速傅里叶变换（FFT）是常用的数据处理手段，MATLAB和python的numpy库等科学计算工具都提供了快速傅里叶变换 fft 函数。

　　但是，调用MATLAB或者python的numpy的 fft 函数对一个信号进行计算，却无法马上得到信号的频谱。我们还需要对函数返回的数据进行处理，才能得到正确的信号频率、幅值、相位等信息，准确绘制信号的频谱图，包括幅度谱和相位谱。

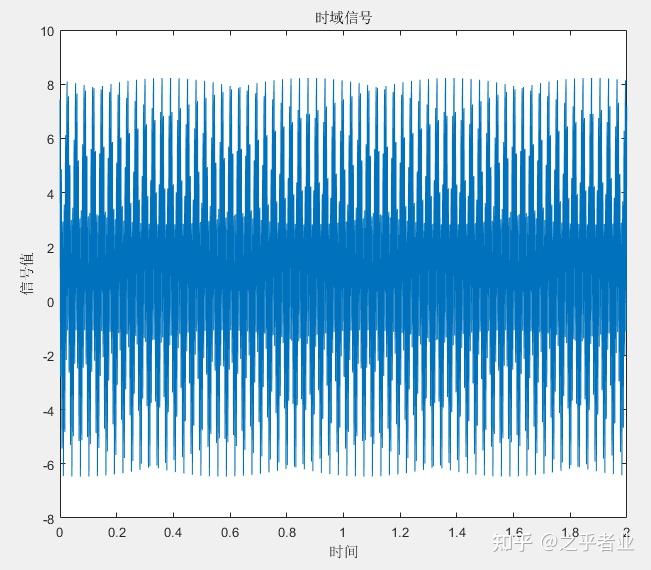
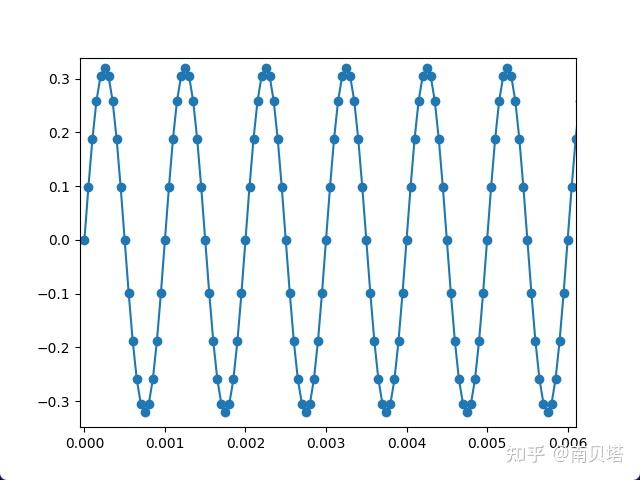
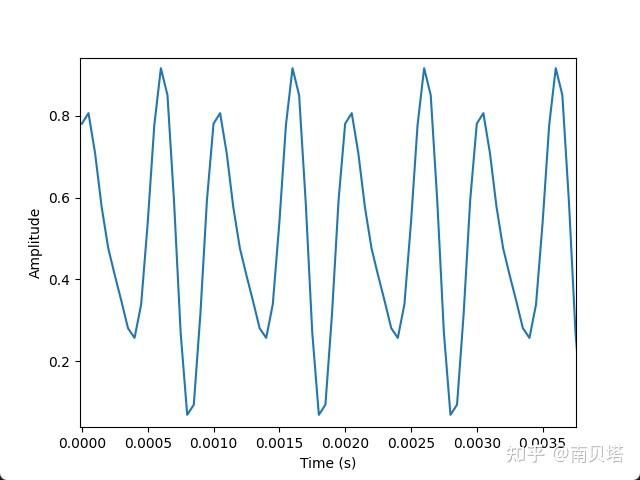
　　考虑一个频率为1 kHz、幅度为0.32的离散正弦波信号，它由许多个离散的点构成，每个点的时间间隔是0.05 ms，即采样频率是20 kHz。其时域波形如下：

　　使用Python，调用numpy的fft函数对其进行快速傅里叶变换：

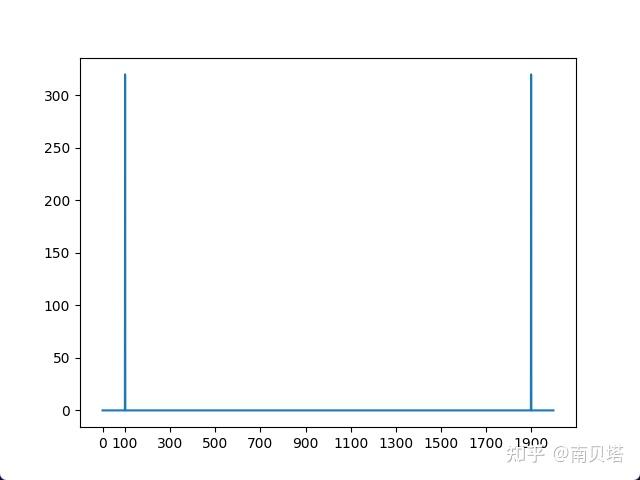
　　直接绘制函数所返回的数据 y 的绝对值，尝试绘制其幅度谱，得到的曲线是：

　　曲线存在两个尖峰，其横坐标分别是100和1900，尖峰对应的横坐标与信号的频率不对应，尖峰对应的纵坐标与信号的幅值不对应，因此这个还不是正确的频谱图。

　　为了得到正确的频谱图，包括幅度谱和相位谱，我们需要对 fft 函数返回的数据进行的一些处理，包括：生成横坐标，令频谱图可以正确反映时域信号的频率。令频谱图中的幅度谱可以正确反映时域信号的幅度。令频谱图中的相位谱可以正确反映时域波形的相位。

　　初学的小伙伴容易绕晕、被劝退。

　　本文在Python中逐步演示对 fft 函数返回的数据的处理过程，并给出完整的 Python 快速傅里叶变换代码，随后同理给出 MATLAB 代码，供自己查阅备忘，也希望可以帮助到有需要的小伙伴。

　　1. 使用Python进行快速傅里叶变换

　　在Python中对时域信号进行傅里叶变换，需要调用numpy库；为了绘图，调用matplotlib库：

　　以20 kHz采样频率生成频率为1 kHz、幅度为0.32的时域离散正弦波信号，该信号为一个一维数组：

　　对离散正弦波信号进行快速傅里叶变换：

　　傅里叶变换得到的数据 y，同样是一个一维数组，其长度等于时域信号 x 的数组长度。数组 y 的每一个元素是一个复数，对应一个频率点的信号幅值和相位信息。数组的第一个元素对应的频率为0，即直流；最后一个元素对应的频率为Fs，即时域信号 x 的采样频率。

　　据此，生成频率点数组，作为频谱图的横坐标，来与数组 y 的每一个点一一对应：

　　现在绘制频谱图中的幅度谱：

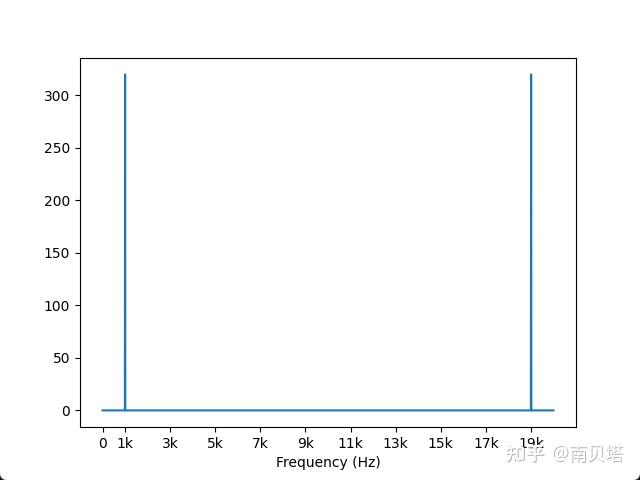
　　现在，曲线图仍然有两个尖峰。

　　对于第一个尖峰，其横坐标是1000，这与时域信号的频率1 kHz相符。

　　对于第二个尖峰，由于时域信号只有一个频率成分，因此其幅度谱不应该有第二个尖峰。第二个尖峰是傅里叶变换算法所生成的信号的镜像副本，该副本对应于信号的负频率。

　　据此，对于数组 y 和横坐标数组 freq，只取其1/2长度来绘制幅度谱，以消除镜像副本：

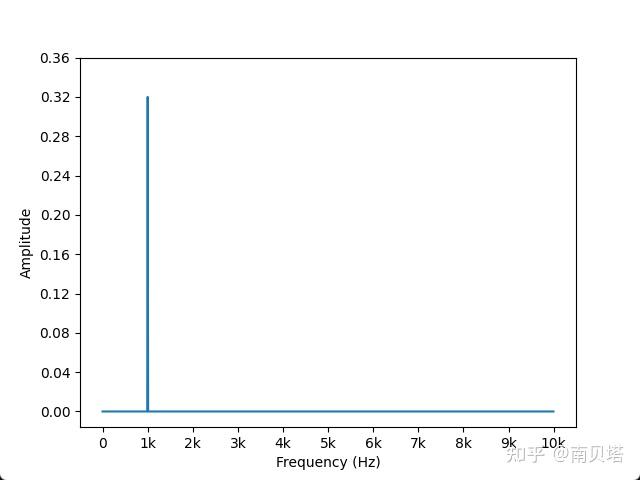
　　现在，曲线图只有一个位于1 kHz的尖峰，此时曲线图所表述的频率成分与时域信号完全相符了，我们完成了对幅度谱横坐标的生成和处理，这个横坐标数组同时也适用于相位谱。

　　可以看到，谱图横坐标最大的频率点为采样频率的一半 fs/2=10 kHz（拓展阅读：奈奎斯特采样定理）。

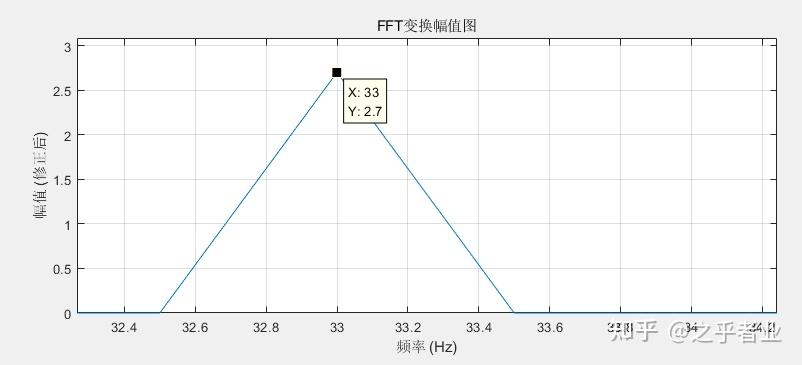
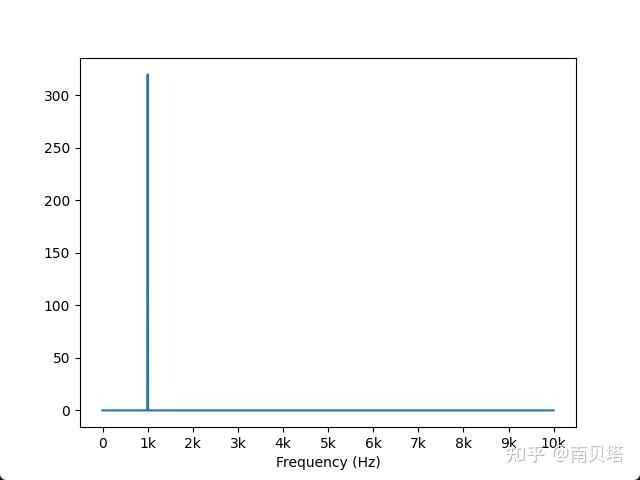
　　观察目前的幅度谱，发现尖峰的幅值为320，与时域信号的幅值0.32不符。因此我们还需要对数组 y 的幅值进行修正。

　　幅值“不准确”同样是由快速傅里叶变换的算法决定的。简单来说，参考 @知乎者业 的文章，这是因为快速傅里叶变换的本质是离散傅里叶变换，所得到的频谱是用功率谱密度（PSD）定义的，其幅值表示的是单位带宽的幅值，而非真实幅值。N个实数点经过离散傅里叶变换之后的频谱带宽为 N/2，每一个频率点所占的带宽为 2/N；而对于第0和第 N/2 个点（对应频率为直流和 fs/2），它们的带宽只占中间频率点的一半，也就是占1/N的带宽。需要据此对每个频率点的幅值进行修正才能得到真正的幅值。

　　修正的方法是，在数组 y 中，对于频率为0的点和频率为 fs/2的点，其幅值需要乘以 1/N；对于其他频率点，其幅值需要乘以 2/N：

　　现在曲线图中尖峰的频率为1 kHz，幅值为0.32，正确反映了时域信号的频率和幅值，我们顺利得到了信号的幅度谱。

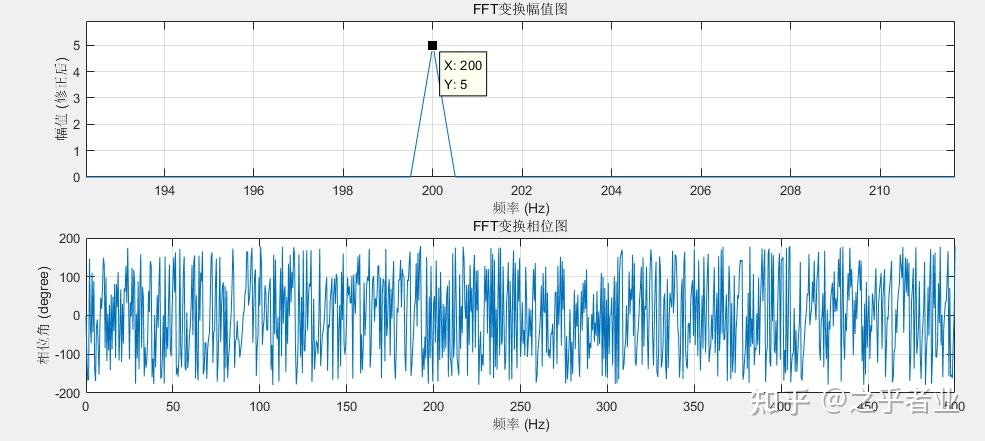
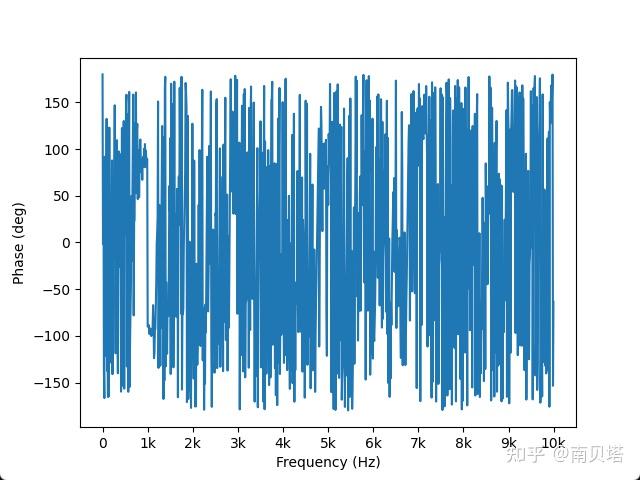
　　fft 函数所返回的数组 y，其每个元素都是一个复数。我们取复数的绝对值，则得到信号的幅值；利用反切计算取复数的角度，则可以得到信号的相位。据此绘制相位谱：

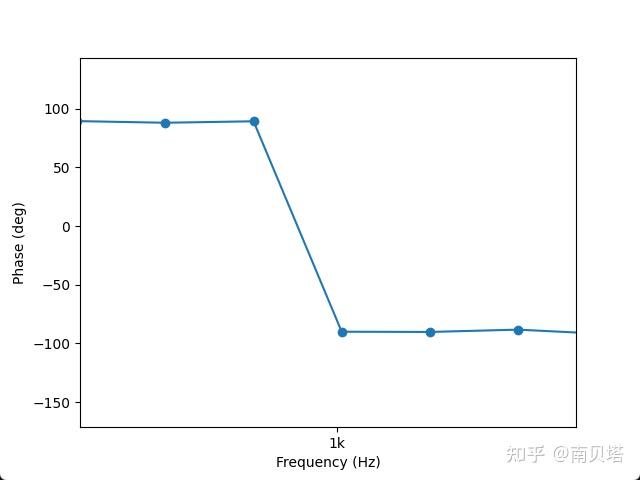
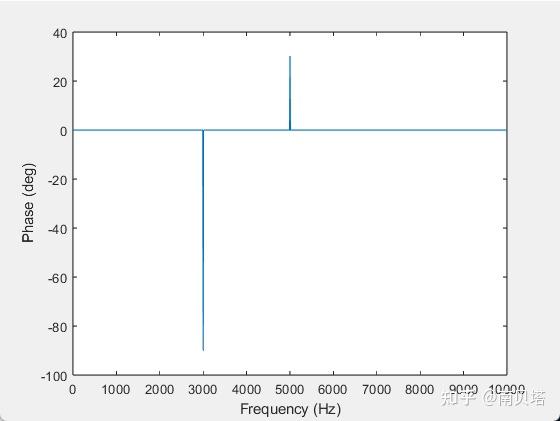
　　可以看到所得到的相位谱充满了噪声，这是由于计算时取数组 y 的元素的虚部和实部进行反切运算，每一个元素（每一个频率点）的虚部和实部都不是0，而是很小的浮点数，那么反切计算也会得到数值，导致相位谱每一个频率点都产生了相位信息（即使时域信号并没有这些频率分量）。（参考阅读：实战数字信号处理之三从FFT得到幅值和相位信息 – 知乎 (zhihu.com)）相位谱在1 kHz处的局部放大

　　我们放大相位谱在1kHz处的数值，发现其数值为-90°，对应正弦波的相位，是正确的，也就是说，时域信号的相位隐藏在相位谱的“噪声”中。

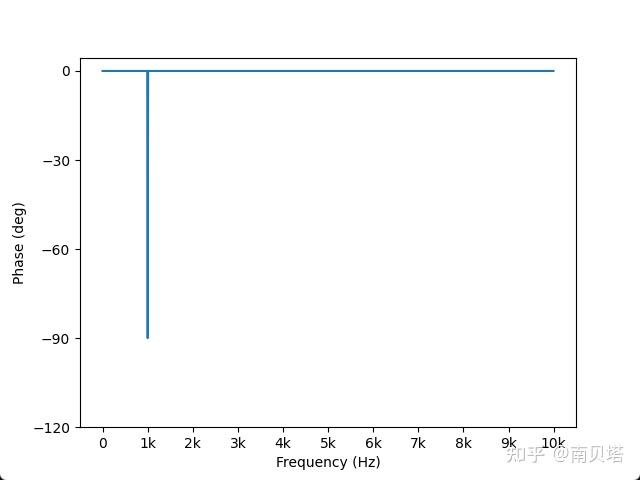
　　我们可以把信号真实存在的频率成分以外的相位信息剔除。方法是利用幅度谱判断频率成分是否真实存在，设置一个阈值，对于数组 y 的每一个元素，如果其幅值低于该阈值，则认为这个元素对应的频率成分不是真实存在的，那么将这个元素置零，以避免在这个频率点计算产生错误的相位信息。

　　现在，我们得到了一个“干净的”相位谱，谱图上在1 kHz处存在一个-90°的尖峰，对应时域信号正弦波的相位。

　　至此，我们获得了时域信号正确的幅度谱和相位谱。

　　完整的Python代码如下：

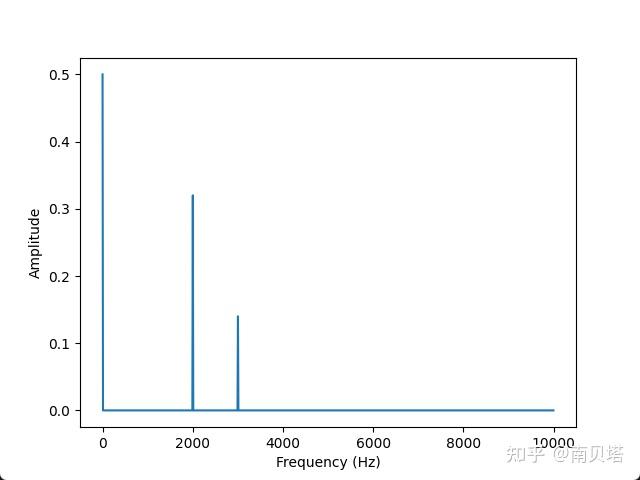
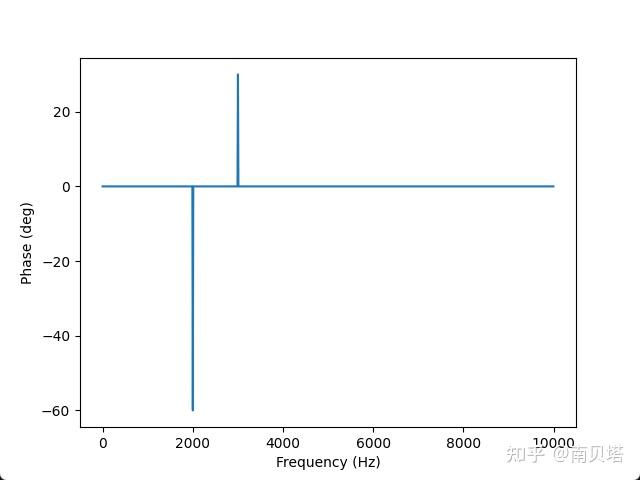
　　尝试另一个时域波形：

　　波形包含3个频率成分：直流成分，幅值0.5频率2 kHz，幅度0.32，初始相位30°频率3 kHz，幅度0.14，初始相位120°

　　使用代码计算其幅度谱和相位谱，成功验证代码的准确性：

　　2. 使用MATLAB进行快速傅里叶变换

　　同理，完整的MATLAB代码如下：

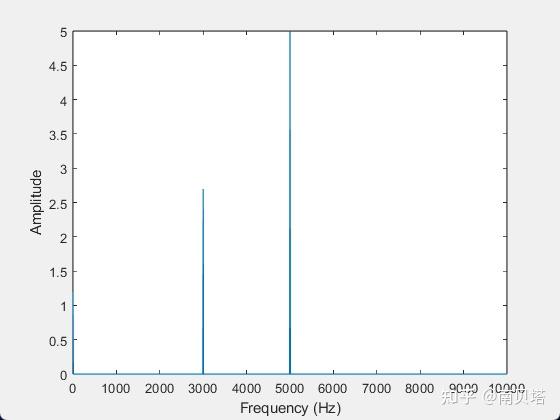
　　调用该函数，对时域波形进行快速傅里叶变换，绘制得到幅度谱和相位谱：

　　3. 总结和补充

　　在科学计算中生成或者物理世界中测量得到的时域数据，通常都是离散的。因此本文所给出的Python和MATLAB快速傅里叶变换程序，可以适用于对一维时域数据进行傅里叶变换并其幅度频谱和相位频谱图。

　　程序的两个输入，一个是波形数据，这个自然是可以的。另一个是这个波形数据的采样频率，如果波形数据是在科学计算中用代码生成的，那么采样频率可以从代码中；如果波形数据是使用示波器等仪器测量得到的，那么采样频率从仪器的设置中。

　　感谢阅读，春节快乐 ！