1. 数字信号基础知识与matlab实现
文章整理了数字信号处理的三个基础且常用的知识点及其matlab实现,包括信号的频移实现、信号时域取实部对频谱的影响、信号的时域上采样及其对频谱的影响。都尝试进行了公式的推导以及matlab仿真实现与验证。
1. 基础知识与准备工作
1. 欧拉公式
欧拉公式为: 

2. DFT与IDFT公式
DFT:
IDFT:
3. matlab仿真原始信号生成
在下面的章节中仿真数字信号的频移、时域取实部以及时域上采样时,均用到了同一个生成的原始信号,因为生成信号的过程有些长,为防止后续占用过多篇幅,所以在本节中,先附上生成原始信号的代码,得到原始信号频谱Pream_frq,与相应的信号时域Pream_time。原始信号使用1024点fft,采样率为25MHz。
生成的原始信号频谱Pream_frq为: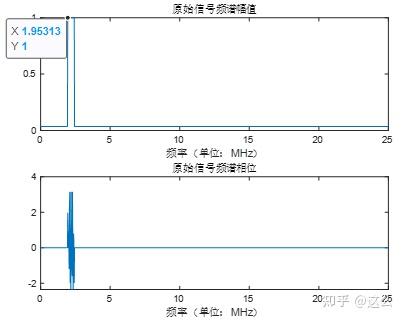
2. 数字信号的频移
1. 公式推导
本节提供了使用Matlab在频域进行移频和在时域进行移频的两种方法,所以先进行了时域移频的公式推导,假设需要在频域向右移 
即
2. matlab仿真
下面的代码分别从频域和时域实现了对原始信号Pream_frq向右频移128点的功能(若想向左平移可设l为负数):
下面画出代码运行生成的原始信号频谱和分别在频域和时域进行频移后的频谱(为方便观察频移的点数,横坐标改为频点值,而不是频率值),根据图中的标注可以看到第80点移位到了第208点,且在频域和时域实现频移后结果完全一致。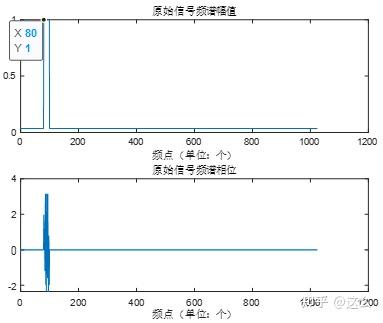
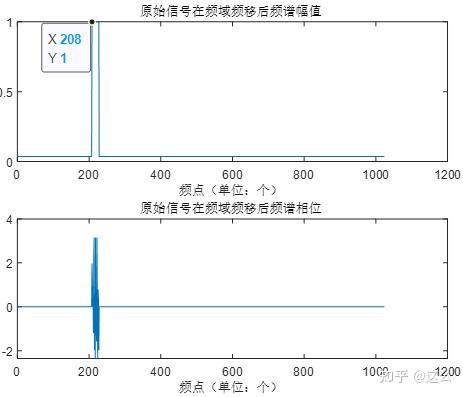
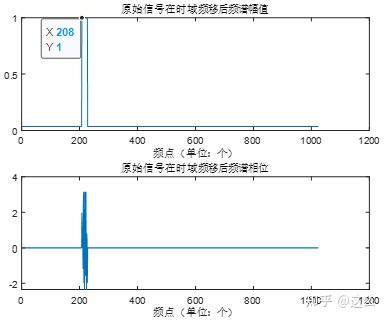
3. 数字信号在时域取实部对频谱的影响
1. 公式推导
首先,

即
原本的IDFT公式 
类比得到




即,
2. matlab仿真
代码如下:
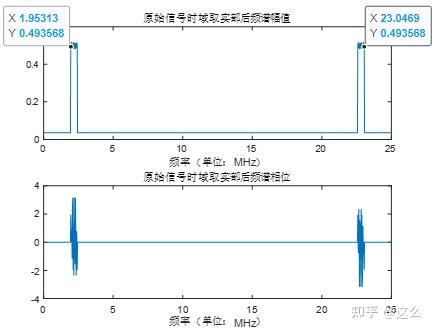
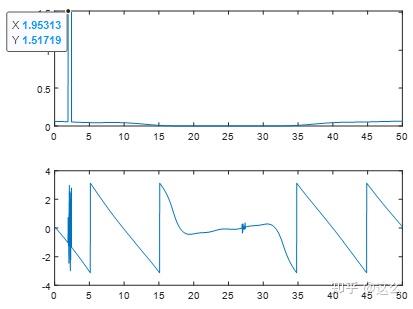
代码运行生成的结果图如下,可以观察到由公式推导得到的结论,取实部后,在与1.95MHz关于12.5MHz对称的位置23.05MHz处出现较高的频谱值。且频谱幅值从单边的1,变为双边的0.5左右,观察频谱相位可以发现,两边的相位是奇对称的,即双边的频谱值是共轭对称的。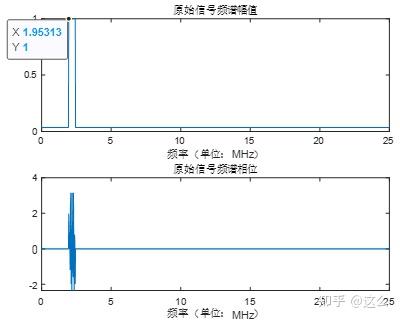
4. 数字信号的时域上采样实现,及其对频谱的影响
1. 公式推导
本节首先公式推导了把N点x(n)二倍上采样至2N点 


首先,

则,
(tip:因为X(k)中k的范围是[0,N-1], 

① 求[0,N-1]段 ,
令上式中 
则
② 求[N,2N-1]段,
令上式中
则
因为始终有
所以
————————
即
也就是时域的2倍上采样在频域上表现为频域扩展。
2. matlab仿真
代码如下:
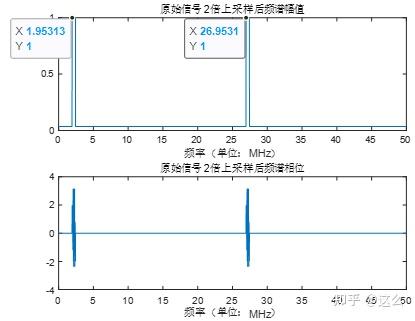
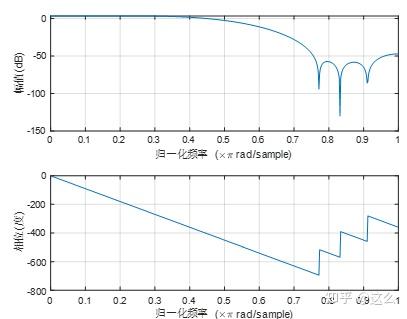
代码得到的仿真图如下,25MHz的原始信号插零后信号频谱与公式推导一致,得到了频谱的扩展。另外,为了把信号能量集中在原来的频段上,插值后,还需通过滤波器滤除其他频段,得到最终的50MHz采样率,且能量还集中在原来频段上的信号。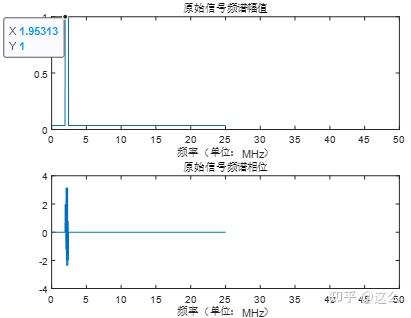
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/92273.html