matlab位与运算_matlab 位运算符

Matlab入门笔记（上）基础语法
　　分为上下两个部分，上篇是基础语法；下篇是应用，主要有MATLAB图像处理。

　　代码和全部内容见MATLAB笔记-github仓库

　　下篇内容是图像应用：omega：

　　本篇内容是曾经学习matlab笔记的整理

　　Q:how to improve my coding force level

　　A:我会找个教程/文档例子，把代码逐行敲一遍，感觉就像是我自己写的一样，一旦完成，我会从头重写一遍，添加注释，并根据自己的用例修改它。

　　一、变量与运算

　　（一）认识matlab

　　

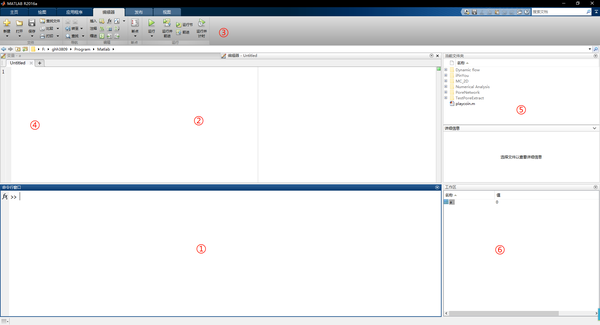
　　我们常规见到的界面应该包括在如图的6个窗口中：

　　1、命令行窗口

　　命令行窗口可以快速运行一些计算或执行命令。当出现提示光标>>时，即代表命令行准备就绪

　　2、编辑器

　　我们总是希望编写完程序后可以自动运行，而不是每次都手动输入命令。在编辑器中，我们可以编辑脚本文件或函数文件，其语法与命令行相同。

　　3、菜单栏

　　菜单栏覆盖了几乎所有的初学MATLAB的操作。例如，我们点击菜单栏中的“主页”->“新建脚本”，将会自动跳转到新的脚本界面。我们编辑以下脚本内容：

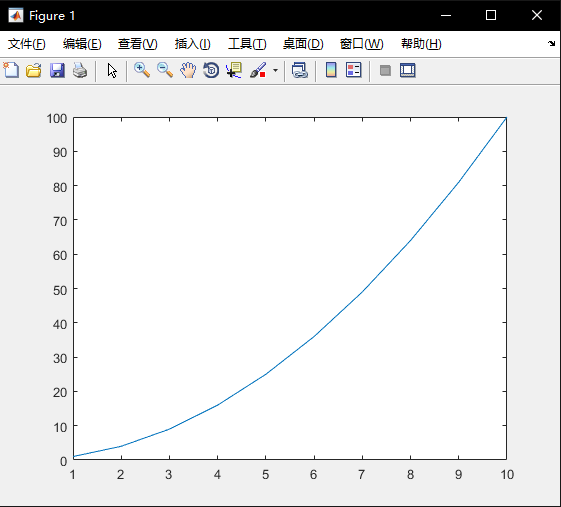
　　点击菜单栏中“编辑器”->“保存”，将脚本文件命名为“Script2_1.m”将结果直接保存至当前文件夹。再次点击 “运行”，即可出现下图所示结果。

　　

　　4、变量

　　在MATLAB或者所有第三代编程语言中，我们用变量操作数据，完成程序的功能。

　　它用特殊的组合，一般以有意义的英文字母开头，来表示数据。

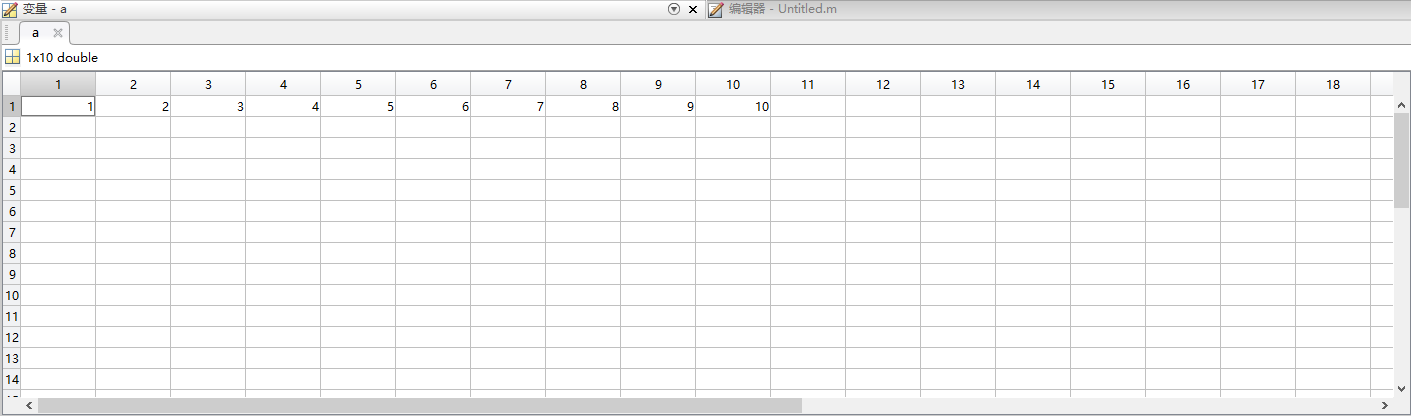
　　接着，运行完刚刚的程序，可以看到我们的工作区中目前有a，ans，b三个变量。我们双击a变量，即可打开变量窗口。可以看到下图所示的内容。

　　

　　“1×10 double”表明该变量的大小为1行×10列，每个元素的类型均为double（双精度浮点数）。以此点击别的变量，我们可以看到对应的变量内容。

　　需要注意的是，在变量窗口中，变量的值是可以直接被修改的。双击其中的一个元素，即可对元素进行更改。

　　5、当前文件夹&详细信息

　　同菜单栏下方的地址栏一起，表明你当前的工作位置。正常情况下，当前文件夹中显示的文件夹均为透明，表明这些文件夹处于不可用状态，即不在你的工作区当中。

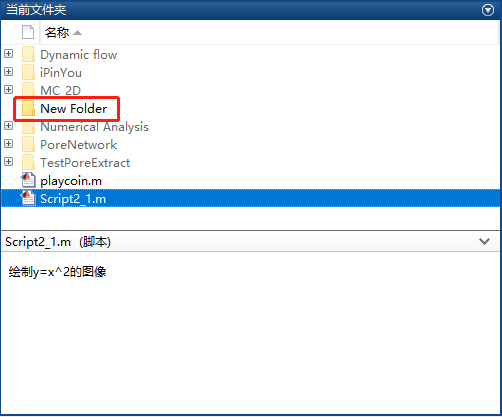
　　这两者有什么区别呢？我们在当前文件夹中右键，创建一个新文件夹。接着，我们再次创建一个脚本“Script2_2.m”，并保存至新创建的文件夹下。这时我们在命令行窗口中输入“Script2_1”，可以看到之前编写的程序重新运行。但是我们如果输入“Script2_1”，将会提示“未定义函数或变量 ‘Script2_1’。”这就是因为我们新创建的文件夹并不属于当前工作区导致的。

　　解决方法就是右击新建的文件夹文件夹，选择“添加到路径”，根据情况选择是否需要添加子文件夹即可。这时我们可以看到，原本透明的文件夹已经变得不透明，其中的脚本文件也可以成功运行。

　　如果我们选择“Script2_1.m”，可以看到详细信息中出现了“绘制y=x^2的图像”，这正是我们编写脚本时开头的注释。因此这里希望大家养成良好的习惯，在编写脚本时在开头使用注释简单说明程序功能，以方便之后的查找。

　　PS：在当前文件夹中，可以进行各种常规资源管理器操作，例如复制、粘贴、重命名等。

　　

　　6、工作区

　　工作区显示了当前状态下的所有变量情况，包括名称、值等。左键标题可以进行排序，右键标题即可选择显示的内容，双击变量即可打开变量窗口。

　　另外，在工作区中选择变量后，按Del键可以删除变量。

　　如果想快速清除所有变量，可以在命令行中输入clear。当不清楚一个功能时，在命令行窗口输入用 help + 查询函数会有官方解释，（网上查也是一种选择）有用的函数指令 clc: 清空命令行窗口 clear: 清空工作变量区的所有变量 close all； 关闭建立的所有窗口

　　（二）基本数据类型

　　接下来我们将学习MATLAB中的各种数据类型，主要包括10种基本数据类型和4种复合数据类型。

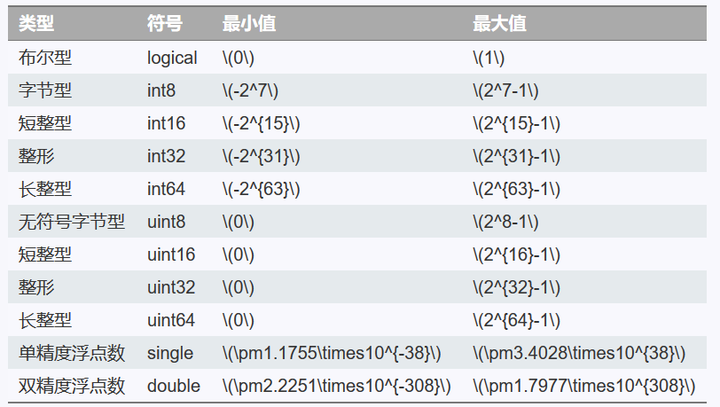
　　和一般的编程语言一样，MATLAB的基本数据类型分为两种，即整型(int)和浮点数(float)。其中整形根据其是否包含负数可以进一步分为有符号整形和无符号整形，而浮点数根据其精度不同又可以进一步划分为单精度浮点数和双精度浮点数。下面的表格列出了各种基本数据类型对应的表示范围，这里类型名称沿用了一般编程语言中的名称。

　　(图像初期用到的基本数据类型是unit8和double类型。)

　　

　　在MATLAB中，不显式指定数据类型的情况下，默认所有的数据类型均为double类型。如果需要创建一个其他类型的变量，只需要加上其符号名即可，例如

　　MATLAB中，有几个特殊的常量，它们分别是：

　　（三）复合数据类型

　　1、矩阵

　　类似一般编程语言中的数组，MATLAB中也有很多复合数据类型，可以将众多基本数据类型合并到一起。最为常见的符合数据类型包括矩阵，结构体和元胞矩阵。

　　矩阵是MATLAB中的基本运算单元，即使是一个数在MATLAB中也是被当做1*1的矩阵看待的。矩阵由若干维度组成，例如0维矩阵表示一个元素，1维矩阵表示一个向量，还有2维、3维甚至更高维的矩阵。在MATLAB中，常规矩阵的最小维度为2维，即一般数学意义上的矩阵，而标量、向量都是矩阵的特例。下面我们将以2维矩阵为例，介绍其生成与运算。

　　（1）矩阵的生成

　　直接输入

　　利用直接输入的方法，我们可以生成一个矩阵。输入的矩阵用中括号表示，同一行元素之间使用逗号或空格分开，用分号或回车结束一行的输入。例如

　　当输入的矩阵不指定变量名称时，结果将暂时保存到ans变量中，即

　　如果没有及时保存结果，ans变量中的内容将会被下一次不指定变量名称的输出结果覆盖。通过函数生成

　　MATLAB中有一些好用的函数，用于构造一些具有特殊性质的矩阵。例如常用的构造函数：

　　类似的函数还有rand()（生成随机矩阵）, magic()（生成幻方矩阵）等，大家可以自行尝试。

　　（2）矩阵计算

　　MATLAB中提供了以下的矩阵运算符

　　在使用矩阵运算符的过程中，应使得操作矩阵符合矩阵运算性质。例如

　　特别的，当加法、减法和乘法作用于矩阵和标量时，代表对矩阵中每个元素进行对应的处理，例如

　　另外，对于左除和右除，其用法如下：

　　除此之外，矩阵还有一些特殊的运算，称之为“点”运算，使用较多的包括.*（点乘）和.^（点乘幂）。点运算的特殊之处在于，它不是按照矩阵的运算规律进行计算的，而是对具有相同大小的两矩阵，将对应元素进行乘或乘幂的操作。例如

　　（3）冒号运算符与矩阵拼接

　　在MATLAB中，:（冒号运算符）是非常重要的一个符号，利用冒号可以轻松表示等差数列。例如

　　取出矩阵元素时，我们只需要指定选取的行号与列号即可。请注意，MATLAB中所有下标均从1开始而非从0开始，请一定牢记！！！

　　基于此，我们可以对长度吻合的矩阵进行拼接，例如

　　除了冒号运算符，还有一种生成等差数列的方式，即使用函数生成从a到b共n个数值的等差数列。同样的，利用可以生成从(10^a) ~ (10^b)共n个数值的等比数列。例如

　　注意，无论使用冒号运算符，或是函数，生成的矩阵均为1*n的矩阵，即为行向量。使用转置符号可以将其转置为列向量。

　　2、复合数据类型——字符串

　　上面介绍的所有类型均为数字类型的变量。而最常见的非数类型的变量就是字符串了。MATLAB中，使用单引号表示字符串：

　　字符串是一个特殊的行向量，其每个元素是一个字符。

　　字符串的拼接类似数组的拼接，但是需要注意由于字符串是行向量，只能进行横向拼接，否则将会报错。

　　字符串和数字之间的转换也十分容易，可以利用num2str()和str2num()函数进行：

　　3、复合数据类型——结构体（了解）

　　结构体是一种特殊的数据类型，是由“变量”和其拥有的“字段”共同组成的，在初学阶段可能见到的比较少，更多的是调用MATLAB内置函数后生成的结构体变量。例如一个学生，他拥有姓名、年龄、期末成绩三个“字段”。利用“.”点运算，我们可以这样定义一个学生：

　　可以看到，随着我们不断向student变量中增加字段，其包含的信息也越来越多。同样的，我们也可以使用struct(filed,value,…)的方式直接生成结构体：

　　如果想要了解更多关于结构体的用法，可以查阅MATLAB的帮助文档。

　　4、复合结构类型——元胞矩阵（了解）

　　元胞矩阵是矩阵的一种扩展，虽然直到现在我也不知道这个名字是怎么取出来的。在矩阵中，一个元素代表的都是一个数，或者都是一个字符。但是在元胞矩阵中，这种限制被打破，不同位置可以拥有任何类型的元素，包括字符串，数值或矩阵。为了区分元胞矩阵和普通矩阵，我们使用大括号进行定义，在使用元素时，也是用大括号对其进行取出。

　　可能你在尝试的过程中也发现了，利用小括号也能对其元素进行取出。关于这两种方式有何不同，我们将在之后的一篇关于元胞矩阵的讨论中再次提到。同样的，MATLAB的帮助文档永远是你的好帮手。

　　（四）流程控制

　　通过前面的内容，我们已经对MATLAB中的数据类型和一些简单的命令有所了解。这篇文章将主要介绍一下MATLAB中的流程控制语句，包括顺序执行、条件控制和循环控制。相信经过这篇文章的学习，你已经可以写出像模像样的MATLAB程序了。

　　1、顺序执行

　　可能你已经注意到了，我们之前的语句都是在命令行窗口中进行编写的。这样虽然可以及时得到反馈，但是如果我们想要同时执行多个语句则是非常困难的。因此我们将利用MATLAB的脚本m文件，使其从一个“大计算器”变成一个“编程工具”。

　　顺序执行是程序执行过程中最基本的执行方式，在MATLAB中也不需要对其进行任何的控制，只需要把要执行的命令按顺序写下来就可以了。例如我们需要对下面的方程组进行求解：

　　我们可以在m文件中编写以下内容。需要注意的是，如果语句不以分号结尾，则会将输出发送到命令行窗口；而如果是以分号结尾，程序虽然运行了，但不会产生任何输出：

　　2、条件执行

　　顺序执行显然不能满足我们的需要，如果我们要操作的语句是根据一定的条件进行选择，那么我们就需要用到条件语句。

　　（1）if条件语句

　　最为常见的条件语句即为if条件语句，其使用方法包括以下两种：

　　为了方便对控制条件进行编写，这里介绍常见的关系运算符和逻辑运算符。常用的关系运算符包括以下几个：

　　和其他编程语言类似，注意逻辑判断中的==（等于）和赋值语句中的=（赋值）的区别。

　　常用的逻辑运算符包括以下几个：

　　注意在MATLAB中，FALSE的值默认为0，TRUE的值默认为1；在进行逻辑运算时，所有的0值被当做FALSE处理，非0值被当做TRUE处理。举例说明：

　　拓展 MATLAB提供位运算符，分别是&（按位与），|（按位或），~（按位非） MATLAB提供的逻辑运算符支持短路操作 MATLAB中不提供++、+=等类似的赋值操作符

　　举一个栗子，如果一斤栗子10元，买5斤及以上总价打八折，计算价格的程序可以这样编写：

　　（2）if嵌套语句

　　if语句是可以进行层层嵌套的，例如下面是两种常见的嵌套模式：

　　通过if语句的嵌套形式，我们可以对运行流程进行更好的控制。再举一个栗子，刚刚的栗子如果买10斤及以上则总价打7折，则计算程序如下：

　　（3）switch语句

　　当我们要判断的分支非常多时，如果使用嵌套if语句写法，将会显得十分繁琐。这时我们可以使用switch语句来使得程序可读性更强。

　　switch语句的用法是这样的。

　　当variable的值可以匹配上其中的任何value时，会直接跳转执行其对应的语句；如果没有匹配上任何值，则会直接跳转到otherwise语句进行执行。需要注意的是，otherwise语句并不是必须的。

　　不同于其他语言的switch语句，如果多个值对应同一个执行语句，可以利用大括号将值写在一起。这也意味着MATLAB不需要在每一个分支后使用break进行显式中断。

　　我们可以编写一个根据年份和月份判断该月有几天的程序：

　　在这个例子中，我们在switch语句内部再次使用了if语句，用于对闰年的判断。其中mod(a,b)函数表示a对b的模。

　　3、循环执行

　　流程控制中的循环语句非常重要，它避免了我们写几乎重复的代码，而通过程序的循环与退出对其进行控制。常见的循环执行语句有while循环和for循环。

　　（1）while循环

　　while循环是最容易理解的一种循环，其用法如下所示：

　　当condition条件为真时，循环执行statement语句，然后再次判断condition条件，直至condition条件不再满足时退出循环。如果在进入while循环前，condition条件不满足，则循环直接不会执行。

　　我们以经典的“水滴数”计算为例，练习while循环。水滴数是这样计算的：对于任意一个正整数，如果它是奇数，则乘3再加1；如果它是偶数，就除以2。循环往复，最后终将变成1（该结果尚未被证明，但至今未发现反例）。

　　（2）for循环

　　回顾一下高斯的优秀事迹：如果要计算1到100的和，如何写这个循环呢？我们当然可以采用如下的while循环的方式进行编写：

　　但是除了while循环外，还有一种更加方便的计数循环：for循环可以快速解决这个问题。for循环的格式如下：

　　其中value一般是利用冒号运算符得到的等差数列。我们利用for循环改写一下求和程序：

　　可以看到使用for循环后整个程序变得更加简洁易懂。同样的，我们还可以求100以内所有奇数的平方和：

　　我们可以看到，使用for循环避免了编写复杂的循环控制条件，使得程序编写者可以直接确定循环的次数和循环变量的值。而当循环次数未知时，则仍需要使用while循环对其进行控制。

　　二、函数

　　在我们已经可以编写简单的MATLAB脚本之后，我们需要学习一个更加强大的编程工具：函数。这篇文章将主要介绍MATLAB中函数的使用。

　　（一）函数的思想

　　之所以说函数是一种强大的工具，是因为使用函数可以让我们的代码变得更加简洁，同时也给我们模块化带来了很大的方便。

　　以我们在生活中做家务为例，正常情况下，我们需要具体写出做家务的每一步，例如： 擦桌子 2. 洗碗 3. 扫地 4. xxxx 5. 擦桌子 6. 洗碗 7. 扫地 8. …

　　如果我们将其组织成一个函数，那我们每次只需要调用做家务这个函数，就可以实现这样一套流程。

　　定义：做家务 = 1. 擦桌子 2. 洗碗 3. 扫地做家务xxxx做家务…

　　同样，如果我们需要在做家务的过程中添加一项“倒垃圾”，我们只需要在函数端进行修改，而不用对调用部分的代码做任何改动，这样模块化的方法将使得我们代码的可维护性大大增强。

　　（二）函数的定义与调用

　　1、函数的定义

　　了解了函数的作用之后，我们就需要了解如何对函数进行定义。MATLAB中的函数定义包括function保留字、输出变量、函数名、输入参数、函数体几部分：

　　定义函数时，一般通过建立单独的函数m文件进行编写。例如，我们可以定义一个“给定两个数，返回其和”的函数add。因此我们可以首先选择新建 -> 函数选项，新建一个与函数名同名的函数m文件（事实上，函数m文件和脚本m文件没有实质性的不同，但是新建函数m文件时将会自动生成函数结构）。这时我们可以看到MATLAB已经自动为我们生成好了函数的结构。

　　我们将其更改为下面内容：

　　通过这个例子我们可以看到，与一般的编程语言不同，MATLAB没有显式的return语句返回计算结果，而是通过在语句中给输出变量赋值的方法实现返回值。类似的，如果我们的函数具有多个返回值，我们即需要对所有的输出变量进行赋值。

　　MATLAB也支持没有任何输出的函数，此时函数仅需要包含如下部分：

　　一般而言，这种没有返回值的函数使用较少，主要是为了实现一些附加作用而使用的。

　　2、函数的调用

　　定义函数是为了方便我们进行调用。MATLAB中调用已定义的函数非常简单，实际上我们之前已经调用过系统内置函数，例如zeros()、ones()等。调用函数的方法如下所示：

　　与上述我们定义的add函数相匹配的函数调用为

　　这与我们定义函数的形式非常一致。需要注意的是，当输出变量的个数小于函数实际返回的变量个数时，MATLAB将默认从前到后进行返回，并不会引起报错。下面的例子很好的说明了这一点。

　　之所以强调是的运行结果，是因为带有输入参数的函数是无法直接被运行的。但是没有输入参数的函数可以直接被运行，例如下列函数在屏幕上打印出Hello World字样。

　　（三）函数变量

　　——函数作为参数

　　MATLAB一项令人欣喜的功能是可以将函数作为变量看待，其方式为使用’@’字符。例如我们编写了之前的文件后，使用以下命令：

　　我们发现，我们定义的var_fun居然实现了和add一样的功能！这看起来很不可思议，但实际上这正是函数式编程的基本概念。甚至，我们还可以将函数作为函数参数进行传递。例如我们定义了一个函数operate，这个函数接受一个操作两个数的函数（例如add）和两个数字，给出计算结果。我们可以这样定义：

　　上面内容里，将add函数作为参数成功传递给了operate，并给出了正确的计算结果。

　　（四）匿名函数

　　提起函数式编程，就不得不提到大名鼎鼎的Lambda函数。在MATLAB中，同样对Lambda函数提供了支持。为方便不了解函数式编程的同学，下面将统一称之为“匿名函数”。

　　首先回想我们使用函数的流程。我们需要确定函数的输入与输出、函数名，新建函数m文件，编写函数体，然后在主程序中对函数进行调用。但很多时候，我们编写的函数可能往往只有一行或更少，这种情况下单独编写一个函数m文件就显得非常麻烦。甚至有些时候，这个函数我们只需要用一次，能不能不取名呢？匿名函数（Lambda函数）就很好地解决了这个问题。

　　匿名函数的声明如下：

　　匿名函数的形式十分简洁，将整个函数的定义缩减到一行内。例如之前的add函数，我们可以这样进行改写

　　可以看到Lambda函数保持了和原函数一样的功能。我们将之前的Script5_2.m文件进行Lambda函数改写：

　　（五）形参vs实参

　　学过其他编程语言的同学在对待函数时，往往需要急切地弄清楚什么时候函数传递形参，什么时候传递实参呢？

　　先上结论：MATLAB函数永远传递形参

　　没有理解的同学可以通过下面的例子感受一下。

　　假设我现在有一个1*5的矩阵，我现在想让这个矩阵的第一个元素加1，那么有什么办法呢？最直观的想法是这样的：

　　表面上看来，这个函数对于任何传递进来的矩阵mat，都将第一个元素进行了加1操作。我们对其进行一下测试：

　　上面的操作中，mat的值并没有发生任何变化！事实上，无论我们在函数内对传入参数进行什么操作，都不会影响到参数在主程序中的原本值，这是因为MATLAB使用的是“形参传递”。在这个过程中，实际上在MATLAB内部发生了如下的事情：

　　因此，无论我们怎么做，主程序中的值都无法在函数中进行修改。那我们怎样实现上述需求呢？一种方式是可以将mat_copy的值直接返回给主程序，主程序再将mat的值替换为函数返回值。如下：

　　这样做或许显得不美观，但也不失为一种好方法。

　　还有一种方法则是利用全局变量的方法。

　　（六）全局变量

　　在介绍全局变量之前，我们需要先了解一下变量空间。变量空间是指MATLAB计算过程中当前状态可以使用的所有变量。例如在主程序中可以访问在主程序中定义的变量，但是在函数运行过程中就无法使用主程序定义的变量，因此我们说它们属于不同的变量空间。

　　一般而言，MATLAB的变量空间可以有多个，其中所有的脚本m文件共享一个变量空间。

　　之所以传递到函数中的参数不能修改，是因为主程序中传进去的参数是属于主程序的变量空间，当函数开始执行时，主程序的变量就被暂存起来无法改动了。那我们自然想到，能不能利用什么方法，使得一个变量不只是属于主程序呢？答案就是全局变量。全局变量不属于任何一个程序模块，在任何时候都可以被修改。

　　我们使用如下的方式定义或使用一个全局变量：

　　使用任何全局变量前，都要先进行声明，以告知编译器：这是一个全局变量，请不要在局部变量里面寻找。使用全局变量可以对上述的add_one方法进行改写：

　　使用全局变量非常方便，但是需要注意的是，使用全局变量与函数化、模块化的概念完全相悖，大量使用全局变量将使得程序的逻辑控制变得复杂，可读性变差。因此建议大家尽量不要使用全局变量，以免生出“一个月前写的程序自己都看不懂”的悲剧。

　　三、matlab绘图——plot函数

　　为了将计算结果进行可视化呈现，MATLAB提供了诸多绘图功能，可以满足不同可视化的需求。这篇内容将主要介绍使用MATLAB进行二维绘图的入门操作。

　　（一）plot函数介绍

　　提到MATLAB中的二维绘图函数，那一定要提到plot函数。虽然是最基础的二维绘图函数，但是其功能却十分的强大。在开始绘图的学习之前，我们需要知道：

　　MATLAB主要用来处理【数值运算】！

　　这句话虽然不完全正确，但在初学阶段表现的很重要。如同之前提到的，MATLAB的主要运算对象是【矩阵】，因此MATLAB的绘制实际上是根据你提供的数据进行绘图。举个栗子，你让MATLAB绘制所谓y=sin(x)的图像，它做不到；但是根据产生的x、y值序列，MATLAB可以轻松进行绘图。

　　（二）plot函数的基本使用方法

　　plot函数可以根据提供的数据绘制对应的图像，其基本用法如下：

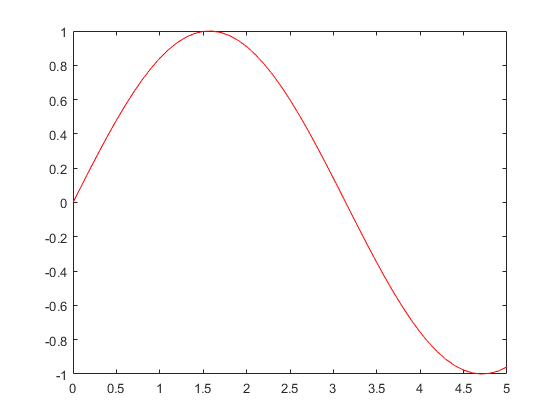
　　例如我们绘制函数y=sin(x)在区间[0,5]上的图像，可以使用以下的代码：

　　绘图结果如图所示：

　　

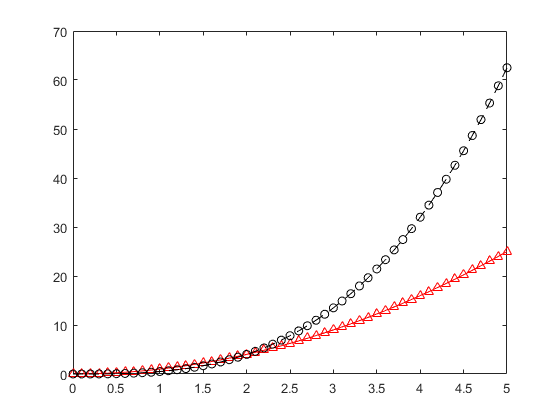
　　同时绘制y=x^2 和y=0.5x^3两个图像：

　　绘图结果：

　　

　　常见的颜色、线型、标记点属性如下：

　　这些属性可以仅指定一种，也可以被同时指定，指定时无需区分顺序。需要注意的是如果指定了标记点类型的话，必须要进一步指定线型，否则绘图时只会出现标记点而没有线。

　　（三）plot函数的额外属性

　　使用plot函数除了可以对颜色、线型、标记点类型进行修改外，还可以通过以下方式设定通用属性值：

　　常见的属性值包括

　　例如下面代码设置了多种参数：

　　绘制出的图像如下所示：

　　

　　（四）添加/设置图像其他部分

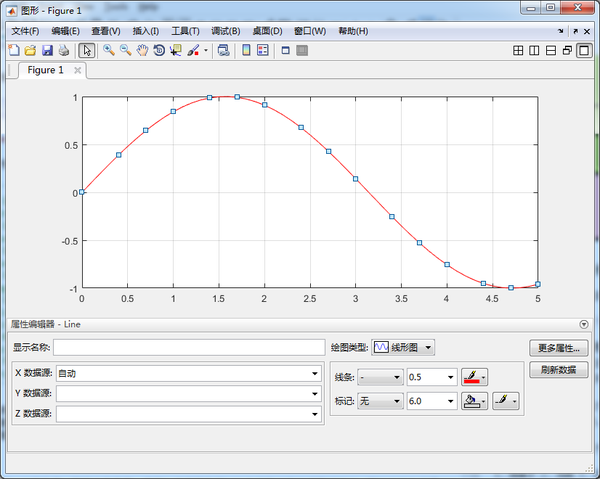
　　一张完整的图表应当包括标题、轴坐标等元素。下面展示了一些常用的添加/设置图表元素的方法。

　　使用代码对图像进行调整，可以使得每次生成的图像具有相同的属性。但是还有一种更加交互化（福利化）的方式，那就是在图像界面进行直接设置。在生成的图像中选择“编辑”->“图形属性”，即可打开对应的交互化设置界面。点击图中的坐标轴、图线还可以对这些元素进行对应的设置。

　　

　　（五）新建图像和添加图像

　　当你想要绘制多张图像时，你可能会发现多次调用plot方法会使得后一次绘制的结果覆盖已有的图像。为了生成新的图像，需要使用以下命令生成一张空白的图像。

　　事实上，在你第一次调用plot()函数时，你可以认为MATLAB已经自动调用了figure方法，生成新的空白图像用于绘图。但之后若没有再次调用figure方法，则每次使用plot()时将覆盖已有的图像。

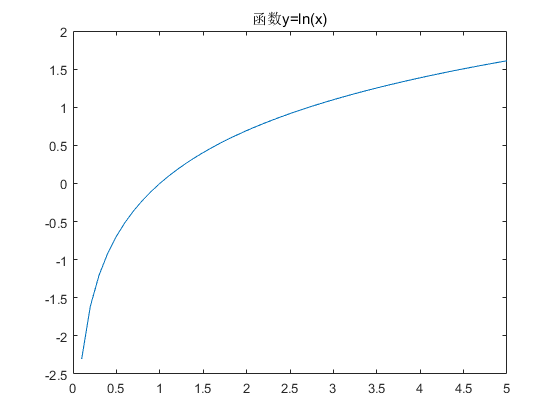
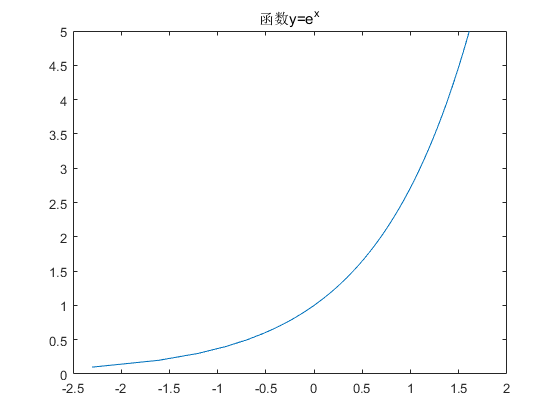
　　例如使用以下代码生成互为反函数的y=ln(x)和y=e^x的两幅图像：

　　Matlab会生成两幅图像：

　　

　　

　　有时我们可能并不想将结果绘制在多个图像上，而是直接绘制在同一个图像上。但是多次使用plot()函数又会使得之前的图像被覆盖，这时就需要使用hold on命令来保持当前图像。

　　hold on命令的使用方法如下：

　　需要注意的是，使用hold on命令之后，两次的plot将完全不相关，等同于在一次plot()函数中同时绘制多组数据。因此使用对于plot()函数出现的多条图线，将不会自动生成直线连接它们。

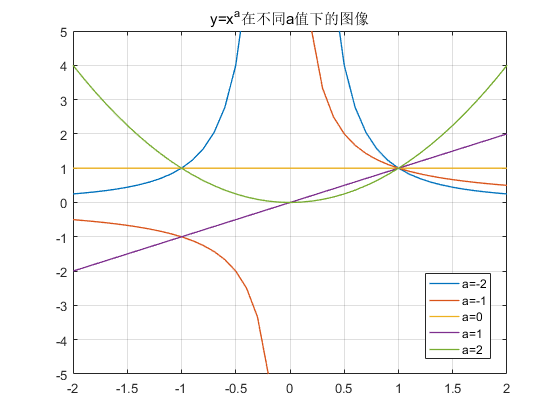
　　使用hold on方法可以使我们绘制图像时不拘泥于将绘图数据全部计算完成后画出，而是使用“更新”的方法进行绘图。例如绘制幂函数y=x^a在不同a值时的函数图像：

　　绘制在同一幅图中的效果：

　　

　　利用hold on还可以作出类似“动态变化”的效果:

　　（六）绘制多幅子图像

　　有些使用我们需要在同一张图中并列放置多张图像，这时候我们可以使用subplot进行绘制。其主要使用方法如下：

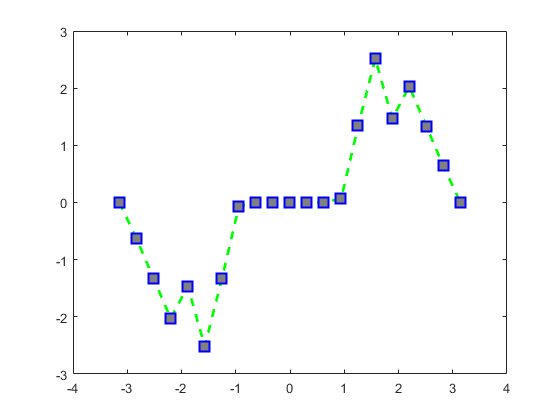
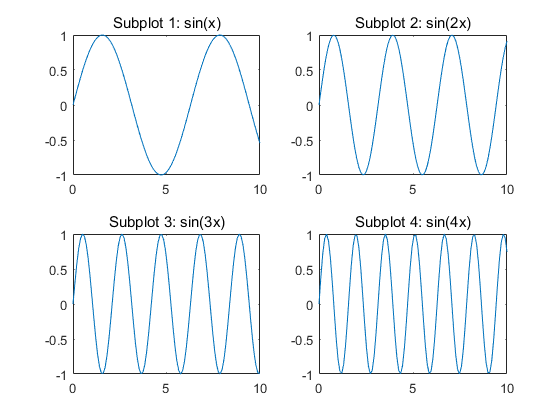
　　需要注意的是，subplot默认按逐行的方式对子图像进行排列。例如以下代码绘制了函数y=sin(k*x)在不同k值下的图像：

　　子图像的绘制结果如图所示：

　　

　　资源链接与参考

　　【1】

　　matlab教学视频：台大 郭彦甫老师

　　MATLAB入门教程

　　【2】

　　灰度图像–形态学处理

　　图像的形态学操作：膨胀与腐蚀

　　【3】

　　数字图像处理:边缘检测(Edge detection) – 郑泽文的文章 – 知乎

　　Sobel边缘检测(matlab)

　　【4】

　　均值滤波、中值滤波【MATLAB】【图像处理】

　　【5】

　　Matlab 彩色图像的直方图均衡化及直方图绘制

　　直方图均衡算法原理