概率里d(x)是什么_概率里dx是什么意思

什么是随机积分？（简版）
　　随机计算（stochastic calculus）是应用于随机过程（stochastic process）的运算，它对随机过程关于随机过程的积分作出定义，由日本数学家伊藤（Ito）创立。在本文中，我们将要对用布朗运动（Brownian motion）定义的随机积分进行一个简单的介绍，所用到的方式没有很强的技术性和理论性，目的是为了让尽可能多的人理解随机积分的概念。

　　1 布朗运动

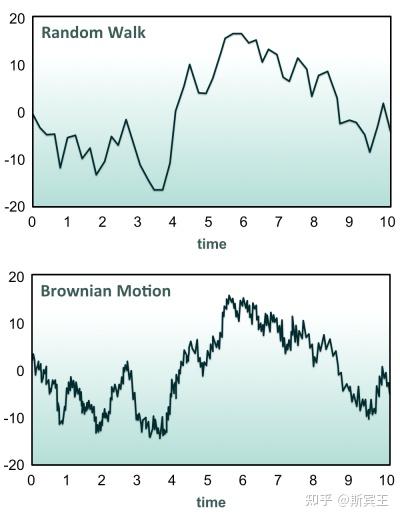
　　布朗运动是指粒子在介质中的随机运动，它由植物学家布朗首次发现。这种运动模式通常包括粒子在流体（fluid）子域（sub-domain）内位置的随机波动，然后重新定位到另一子域。每次重新定位之后，新的子域中会出现更多波动。该模式描述了由给定的温度定义的处于热平衡（thermal equilibrium）的流体。在这种流体中，不存在优先流动方向。更具体地说，流体的整体线性动量（linear momentum）和角动量（angular momentum）随时间保持为零。一个粒子布朗运动的轨迹

　　在数学中，布朗运动又叫维纳过程（Wiener process），它是一个连续时间（continuous-time）随机过程。布朗运动有很多种构造方式，在本文中，我们用随机行走（random walk）的极限来引入布朗运动。

　　定义 1.1 令 $(\Omega,\mathcal{F},\mathbb{P})$ 为一个概率空间（probability space）. 对于一个离散时间（discrete-time）随机过程 $\{X_t\}_{t=0}^\infty$ ，若，且 $X_t=X_{t-1}+\xi_t$ ，这里 $\xi_t$ 是i.i.d的， $\mathbb{E}[\xi_t]=0\ \forall\ t$ ，且 $\mathrm{Var}(\xi_t)=\sigma^2\ \forall\ t$ ，则 $\{X_t\}_{t=0}^\infty$ 叫作随机行走.

　　令 $0=t_0<t_1<\cdots<t_N=t$ 。很容易看出来， $\{X_{t_n}-X_{t_{n-1}}\}_{n=1}^N$ 是i.i.d的，期望为，且方差为 $\mathrm{Var}(X_{t_n}-X_{t_{n-1}})=\sigma^2(t_n-t_{n-1})$ 。将时间区间分为长度相等均为 $\Delta t$ 的子区间。为了简化，我们假设 $\Delta t$ 整除，故一共有 $1/\Delta t$ 个子区间。自然地定义 $X_t=\sum_{k=1}^{t/\Delta t}\epsilon_k$ ，其中 $\epsilon_k$ 是i.i.d的，且期望为。由于 $\mathrm{Var}(X_t)=(t/\Delta t)\mathrm{Var}(\epsilon_k)=\sigma^2t$ ，我们有 $\mathrm{Var}(u_k)=\sigma^2\Delta t$ 。

　　令 $\Delta t\to 0$ ，在时间之间会有越来越多的。根据中心极限定理（central limit theorem），我们有 $X_t-X_s\sim N(0,\sigma^2(t-s))$ 。这样，我们就可以将布朗运动定义为“连续的”随机行走。换句话说，将随机行走视为定义在小时间区间上的期望为且方差取决于区间长度的i.i.d随机变量之和，并令区间长度趋近于，我们会得到有正态（normal）无限小增量累计而成的连续随机过程，即布朗运动。随机行走和布朗运动

　　定义 1.2 若一个连续时间随机过程 $\{W_t\}_{t\ge0}$ 满足样本路径（sample path） $t\to W_t$ 几乎必然（almost surely）是连续的从到的增量独立（independent）于路径 $W_u,u\le s$ ，且 $W_t-W_s\sim N(0,\sigma^2(t-s))$

　　则叫作布朗运动. 通常情况下， $\sigma^2=1$ ，这时叫作标准布朗运动（standard Brownian motion）. 如果 $W^d:\Omega\times[0,\infty)\to\mathbb{R}^d$ 满足样本路径（sample path） $t\to W_t^d$ 几乎必然（almost surely）是连续的从到的增量独立（independent）于路径 $W_u^d,u\le s$ ，且 $W_t^d-W_s^d\sim N(0,(t-s)\Sigma)$ ，其中 $\Sigma$ 是一个半正定的（positive semidefinite）瞬时协方差矩阵（instantaneous covariance matrix）

　　则叫作 -维布朗运动.

　　布朗运动有很多很好的性质。它不仅是马尔可夫过程（Markov process），还是鞅（martingale）。此外，布朗运动还有处处连续（everywhere continuous）处处不可导（nowhere differentiable）的性质。

　　2 随机积分

　　我们想要对用布朗运动来定义的函数进行积分和微分，故引入随机积分的概念。令 $\{\mathcal{F}_t\}_{t\ge0}$ 为一个滤波（filtration），即一个 $\sigma$ -代数（ $\sigma$ -algebra）的升序列（ $\mathcal{F}_s\subseteq\mathcal{F}_t,s\le t$ ）。假设 $a:\Omega\times[0,\infty)\to\mathbb{R}$ 和适应于（adapted to） $\mathcal{F}_t$ ，即 $a_t(\cdot)$ 和 $W_t(\cdot)$ 是 $\mathcal{F}_t$ -可测的（ $\mathcal{F}_t$ -measurable）。若 $a_t(\omega)=a(\omega)$ 关于时间不变，那么可以很自然地定义 $\int_0^Ta(\omega)\ dW_t=a(\omega)W_T$ 。若 $a_t(\omega)$ 是一个关于时间的阶跃函数（step function），即存在 $0=t_0<\cdots<t_N=T$ ，使得 $a_t(\omega)$ 在区间 $[t_{n-1},t_n)$ 上不变。叠加每个子区间上的积分，我们自然地定义 $\int_0^Ta_t(\omega)\ dW_t=\sum_{n=1}^{N}a_{t_{n-1}}(\omega)(W_{t_n}-W_{t_{n-1}})$ 。

　　如果 $a_t(\omega)$ 是cadlag，即在右侧连续（ $\lim_{s\downarrow t}a_s(\omega)=a_t(\omega)$ ），在左侧有极限（ $\lim_{s\uparrow t}a_s(\omega)$ 存在），又可以自然地定义 $\int_0^Ta_t(\omega)\ dW_t=\lim\sum_{n=1}^{N}a_{t_{n-1}}(\omega)(W_{t_n}-W_{t_{n-1}})$ ，这里是对于越来越精细的对的划分 $0=t_0<\cdots<t_N=T$ 取极限。如果我们采用类似于定义黎曼积分（Riemann integral）的论述，我们可以证明，对于任意平方可积的（square integrable）的函数，伊藤积分

　　 $\int_0^Ta_t(\omega)\ dW_t=\lim\sum_{n=1}^{N}a_{t_{n-1}}(\omega)(W_{t_n}-W_{t_{n-1}})\\$

　　都是一个成立的定义。

　　这就是对随机积分或伊藤积分的定义的简单介绍。注意伊藤积分的定义和黎曼－斯蒂尔杰斯积分（Riemann-Stieltjes integral）的定义

　　 $\int_a^bf(x)\ dg(x)=\lim\sum_{n=1}^{N}f(\xi_n)(g(x_n)-g(x_{n-1}))\\$

　　十分类似，这里 $a=x_0<\cdots<x_N=b$ ，且 $\xi_n$ 是区间 $[x_{n-1},x_n]$ 上。这里我们看到了黎曼－斯蒂尔杰斯积分和伊藤积分的区别：在伊藤积分中， $a_{t_{n-1}}(\omega)$ 取值于区间的左端点 $t_{n-1}$ ，而在黎曼－斯蒂尔杰斯积分中 $f(\xi_n)$ 取值于区间的任意一点。黎曼－斯蒂尔杰斯积分的值和被积项（integrand）在区间中的取值点无关，而伊藤积分的值和被积项在区间中的取值点有关。事实上，在另一种随机积分的定义中，被积项的取值点是区间的中点，这样定义的随机积分叫作斯特拉托诺维奇积分（Stratonovich integral）。

　　在随机积分中，我们通常使用像和这样的微分（differential）而非积分。这些微分满足一些法则：

　　首先，由于我们将平均分为份， $t_n-t_{n-1}=\frac{T}{N}$ ，即 $(t_n-t_{n-1})^2=\frac{T^2}{N^2}$ 。那么 $\sum_{n=1}^{N}(t_n-t_{n-1})^2=N\frac{T^2}{N^2}=\frac{T^2}{N}\to0$ ，即。接着，根据布朗运动的定义， $\sum_{n=1}^{N}\sqrt{N}(W_{t_n}-W_{t_{n-1}})^2$ 是期望为且方差为 $N(t_n-t_{n-1})=N\frac{T}{N}=T$ 的独立随机变量。根据大数定律（law of large numbers）， $\sum_{n=1}^{N}(W_{t_n}-W_{t_{n-1}})^2=\frac{1}{N}\sum_{n=1}^{N}\sqrt{N}(W_{t_n}-W_{t_{n-1}})^2\xrightarrow[a.s.]{}T=\int_0^T\ dt$ ，即。然后，由于 $dtdW_t=dt(dt)^{\frac{1}{2}}=(dt)^{\frac{3}{2}}$ ，且 $\sum_{n=1}^{N}(t_n-t_{n-1})^\frac{3}{2}=N\frac{T^\frac{3}{2}}{N^\frac{3}{2}}=\frac{T^\frac{3}{2}}{N^\frac{3}{2}}\to0$ 。

　　我们还可以用其他随机过程，如扩散过程（diffusion process），定义随机积分。

　　定义 2.1 如果随机过程满足 $X_t=X_0+\int_0^tf_s(\omega)\ ds+\int_0^tg_s(\omega)\ dW_s$ ，其中是适应过程（adapted process），那么叫作扩散过程，其中叫作漂移项（drift term），叫作扩散项（diffusion term）. 扩散过程的微分形式是 .

　　显然，对于扩散运动的微分形式，我们仍有，另外。由扩散运动定义的随机积分可被定义为 $\int_0^Ta_t(\omega)\ dX_t=\int_0^Ta_t(\omega)f_t(\omega)\ dt+ \int_0^Ta_t(\omega)g_t(\omega)\ dW_t$ 。

　　3 伊藤引理

　　在微积分（calculus）中，如果我们想要计算定积分（definite integral），我们不是用黎曼积分的定义，而是用微积分基本定理（fundamental theorem of calculus） $\int_a^bf'(x)\ dx=f(b)-f(a)$ ，这对所有绝对连续（absolutely continuous）函数都成立。我们可以将此结论写为微分形式。如果还是关于的函数，在处的泰勒级数（Taylor series）是

　　 $f(t,x)=f(a,b)+f_t(a,b)(t-a)+f_x(a,b)(x-b)+\frac{1}{2}(f_{tt}(a,b)(t-a)^2+2f_{tx}(a,b)(t-a)(x-b)+f_{xx}(a,b)(x-b)^2)+\cdots\\$

　　若将此展开式写为微分形式，由于，我们有。伊藤引理（Ito's lemma）就是随机版的泰勒展开式（Taylor expansion）。

　　令 $\{X_t\}_{t\ge0}$ 为一个有连续路径的随机过程，并令为一个函数。令 $0=t_0<\cdots<t_N=t$ ，并令 $X_n=X_{t_n}$ 。根据泰勒定理（Taylor's theorem）， $f(t,X_t)-f(0,X_0)=\sum_{n=1}^{N}(f(t_n,X_n)-f(t_{n-1},X_{n-1}))$ $=\sum_{n=1}^{N}[f_t(t_{n-1},X_{n-1})(t_N-t_{N-1})+f_x(t_{n-1},X_{n-1})(X_n-X_{n-1})$ $+\frac{1}{2}f_{xx}(\tau_n,\xi_n)(X_n-X_{n-1})^2+f_{tx}(\tau_n,\xi_n)(t_n-t_{n-1})(X_n-X_{n-1})+\frac{1}{2}f_{tt}(\tau_n,\xi_n)(t_n-t_{n-1})^2]$

　　这里 $\tau_n\in[t_{n-1},t_n]$ ， $\xi_n\in[X_{n-1},X_n]$ 。

　　令为布朗运动，并令 $N\to\infty$ ，第一项收敛于 $\int_0^Tf_t(t,W_t)\ dt$ ，第二项收敛于 $\int_0^Tf_w(t,W_t)\ dW_t$ ，第三项收敛于 $\int_0^T\frac{1}{2}f_{ww}(t,W_t)\ dt$ ，第四项和第五项收敛于，因为。这样，我们就得到了伊藤引理

　　 $f(t,W_t)-f(0,W_0)=\int_0^T(f_t(t,W_t)+\frac{1}{2}f_{ww}(t,W_t))\ dt+\int_0^Tf_w(t,W_t)\ dW_t\\$

　　若采用微分形式，可表达为

　　 $df(t,W_t)=(f_t(t,W_t)+\frac{1}{2}f_{ww}(t,W_t))\ dt+f_w(t,W_t)\ dW_t\\$

　　如果是一个满足的扩散过程，那么伊藤引理告诉我们

　　 $df(t,X_t)=f_t(t,X_t)dt+f_x(t,X_t)dX_t+\frac{1}{2}f_{xx}(t,X_t)(dX_t)^2\\ =(f_t(t,X_t)+af_x(t,X_t)+\frac{1}{2}b^2f_{xx}(t,X_t))\ dt+bf_x(t,X_t)\ dW_t\\$

　　所以，如果是一个扩散过程，且是一个函数，也是一个扩散过程。类似地，在多维情况下，若，其中的维度是 $d_x\times 1$ ，的维度是 $d_x\times d_w$ ，瞬时协方差矩阵是 $\Sigma$ ，那么我们可以得到多维情况下的伊藤引理

　　 $df(t,X_t)=f_t(t,X_t)dt+f_x(t,X_t)dX_t+\frac{1}{2}(dX_t)^\top f_{xx}(t,X_t)(dX_t)\\ =f_t(t,X_t)dt+f_x(t,X_t)(adt+BdW_t)+\frac{1}{2}(dW_t)^\top B^\top f_{xx}(t,X_t)B(dW_t)\\ =f_t(t,X_t)dt+f_x(t,X_t)(adt+BdW_t)+\frac{1}{2}\mathrm{tr}[f_{xx}(t,X_t)B(dW_t)(dW_t)^\top B^\top]\\ =(f_t(t,X_t)+f_x(t,X_t)a+\frac{1}{2}\mathrm{tr}[f_{xx}(t,X_t)B\Sigma B^\top])dt+f_x(t,X_t)BdW_t\\$

　　4 随机优化

　　微积分可以被应用于优化问题，而类似地，随机计算也可以被应用于随机优化（stochastic optimization）。随机优化中的变量是随机变量，而如果这个随机变量是由布朗运动定义的扩散运动，我们之前引入的随机积分概念就要发挥作用了。考虑如下问题

　　 $\begin{aligned} \max\quad &\mathbb{E}_0\left[\int_0^\infty f(s,X_s,Y_s)\ ds\right]\\ \textrm{s.t.} \quad & dX_t=a(t,X_t,Y_t)dt+B(t,X_t,Y_t)dW_t\\ &X_0=x_0 \\ \end{aligned}\\$

　　其中连续，关于是，关于是，是状态变量（state variable），是控制变量（control variable），是瞬时协方差矩阵为 $\Sigma$ 的多维布朗运动。

　　我们可以通过推导贝尔曼方程（Bellman equation）来解决此类动态规划（dynamic programming）问题。令

　　 $J(t,x)=\sup_{\{Y_s\}_{s\ge t}}\mathbb{E}_t\left[\int_t^\infty f(s,X_s,Y_s)\ ds\right]\\$

　　为时的价值函数（value function），也就是说，这是在状态的情况下后续变化的最大期望。如果 $\Delta t$ 很小，根据离散时间的贝尔曼方程，我们有 $J(t,x)\approx\sup_y(f(t,x,y)\Delta t+\mathbb{E}_t[J(t+\Delta t,x+\Delta x)])$ $\Leftrightarrow 0\approx\sup_y(f(t,x,y)\Delta t+\mathbb{E}_t[\Delta J])$ ，这里 $\Delta J=J(t+\Delta t,x+\Delta x)-J(t,x)$ 。两边同时除以 $\Delta t$ ，并令 $\Delta t\to0$ ，我们有 $0=\sup_y(f(t,x,y)+\mathbb{E}_t[dJ]/dt)$ 。

　　根据伊藤引理， $dJ=(J_t+J_xa+\frac{1}{2}\mathrm{tr}[J_{xx}B\Sigma B^\top])dt+J_xBdW_t$ ，而由于 $\mathbb{E}[dW_t]=0$ ，我们有 $\mathbb{E}_t[dJ]=(J_t+J_xa+\frac{1}{2}\mathrm{tr}[J_{xx}B\Sigma B^\top])dt$ 。这样，我们就得到了我们想要的贝尔曼方程

　　 $0=\sup_y(f(t,x,y)+J_t+J_xa+\frac{1}{2}\mathrm{tr}[J_{xx}B\Sigma B^\top])\\$

　　此贝尔曼方程又叫HJB方程。HJB方程可以帮助我们解决随机优化问题。如果 $\{X_t,Y_t\}_{t\ge0}$ 满足约束（constraint），那么它叫作可行的（feasible）。下面这个定理告诉我们随机优化问题的解法。

　　定理 4.1 令关于是，关于是，令 $\{X_t,Y_t\}_{t\ge0}$ 为可行的，并令 $\mathbb{E}_0\left[\int_0^\infty|f(s,X_s,Y_s)|\ ds\right]<\infty$ . 如果满足HJB方程，且 $\lim_{T\to\infty}\mathbb{E}_t\left[J(T,X_T)\right]=0$ ，那么

　　 $\mathbb{E}_t\left[\int_t^\infty f(s,X_s,Y_s)\ ds\right]\le J(t,X_t)\\$

　　当是时的HJB方程的解时，等号成立.

　　证明根据HJB方程， $f(s,X_s,Y_s)\le-(J_t+J_xa+\frac{1}{2}\mathrm{tr}[J_{xx}B\Sigma B^\top])$ . 从到积分，我们得到 $\int_t^Tf(s,X_s,Y_s)\ ds\le\int_t^T-(J_t+J_xa+\frac{1}{2}\mathrm{tr}[J_{xx}B\Sigma B^\top])\ ds$ . 由于 $\mathbb{E}[dW_t]=0$ ，取条件期望（conditional expectation）后，有 $\mathbb{E}_t\left[\int_t^Tf(s,X_s,Y_s)\ ds\right]\le-\mathbb{E}_t\left[\int_t^T(J_t+J_xa+\frac{1}{2}\mathrm{tr}[J_{xx}B\Sigma B^\top])\ ds\right]$ $=-\mathbb{E}_t\left[\int_t^T(J_t+J_xa+\frac{1}{2}\mathrm{tr}[J_{xx}B\Sigma B^\top])\ ds+J_xBdW_s\right]=J(t,X_t)-\mathbb{E}_t[J(T,X_T)]$ . 这里我们用到了 $dJ=(J_t+J_xa+\frac{1}{2}\mathrm{tr}[J_{xx}B\Sigma B^\top])dt+J_xBdW_t$ . 令 $T\to\infty$ ，并使用条件 $\lim_{T\to\infty}\mathbb{E}_t[J(T,X_T)]=0$ ，我们得到 $\mathbb{E}_t\left[\int_t^\infty f(s,X_s,Y_s)\ ds\right]\le J(t,X_t)$ .