matlab移位运算_matlab卫星轨道计算

2024年 8月 8日上午9:08 • 激活谷笔记

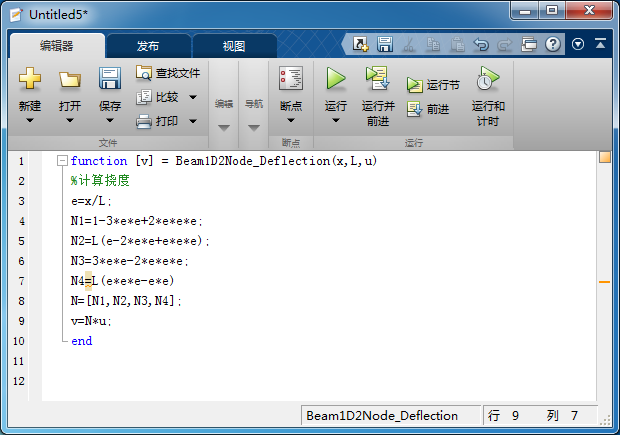
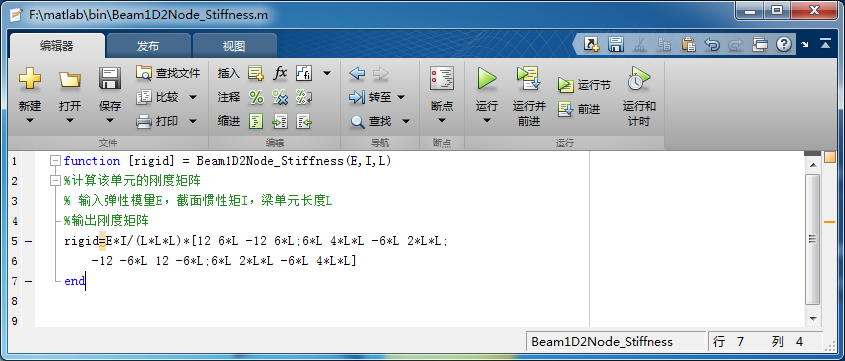
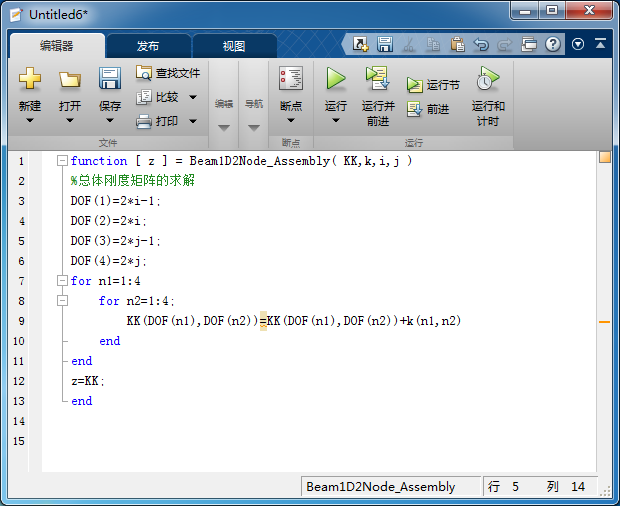
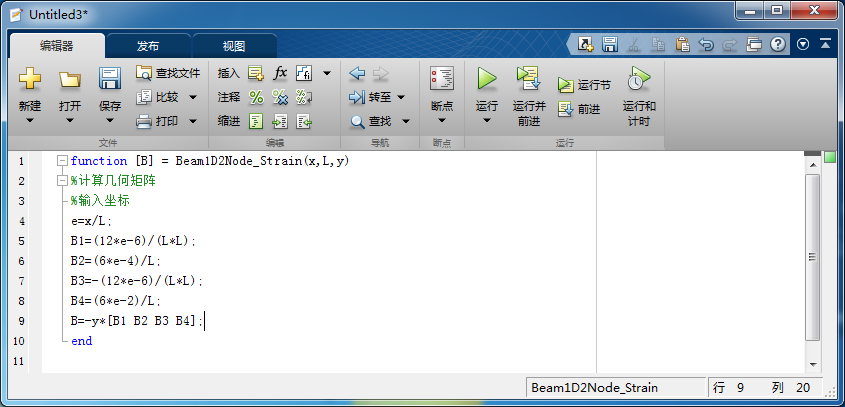
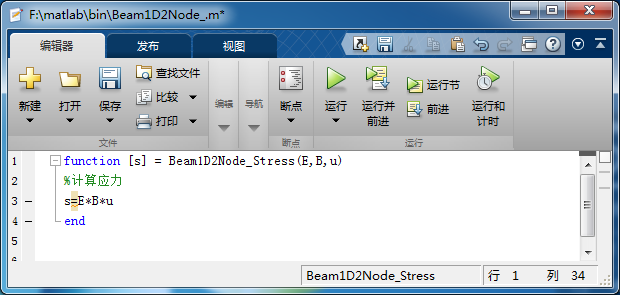
（大四）有限单法的MATLAB编程计算（二）　　引言：之前在QuYln：有限单法的MATLAB编程计算（一）中，写了平面杆系结构的有限分析以及MATLAB编程，ANSYS仿真，等。今天写一下平面梁单的有限分析过程。　　看之前先看这一篇：QuYln：清华MOOC有限课程学习笔记（五）　　参考：清华大学mooc课程（QuYln：固体力学相关视频公开课链接汇总）　　一、局部坐标系下的建模：　　1.局部坐标系下，单的节点描述：　　（1）参数化几何坐标：　　
；　　（2）节点位移列阵（平面梁单有四个自由度degree of freedom）：　　
$\left[ \nu1 ，\theta1， \nu2 ，\theta2\right]^{T}$ ；　　（3）节点力列阵：　　
$\left[ Pv1 ，M1， Pv2 ，M2\right]^{T}$ 。　　2.梁单上场变量的描述：　　（1）位移场：　　note：位移场的描述依据两个条件；唯一确定性以及从低阶到高阶。唯一确定性是指n个自由度就取n-1次多项式，由n个自由度来确定n个系数。　　
$v（x）=a+bx+cx^{2}+dx^{3}$ 　　这样设的目的是因为仅有4个位移参数。　　由节点的位移条件，确定多项式的系数，从而求得位移场。　　这里为了用无量纲的形状函数矩阵和节点位移列阵相乘，故引入无量纲参数
$\xi（\xi=x/l)$ 。　　（2）应变场：　　有了位移场函数，通过几何关系，得到应变场的描述。　　（3）应力场：　　有了应变场，再通本构关系，得到应力场与应力矩阵。　　3.最小势能原理的应用：　　现在我们应用最小是能原理来求解，注意，内力势能和外力势能的系数不同，前者有1/2。　　通过最小势能的一阶变分为0，得到单刚度方程。　　二、MATLAB的编程实现：　　（1）需要定义的函数有，刚度函数，组装函数，应力函数，应变函数，挠度函数。　　（2）单刚度矩阵函数：　　局部坐标下的单刚度矩阵的导出由最小势能原理得到，只需要把单刚度矩阵所需要定义的参数输入即可，即E,I,L。

　　（3）整体刚度矩阵的计算：　　有了局部坐标系下的单刚度矩阵，为了得到总体刚度矩阵，需要进行组装。组装时，根据局部系下的刚度矩阵的标号向总体刚度矩阵进行填充。

　　（4）几何矩阵的计算：　　几何矩阵的计算根据以上求应变得到的矩阵直接赋值即可。

　　（5）应力矩阵的计算：

　　（6）挠度计算：

matlab移位运算_matlab卫星轨道计算

相关推荐