b树和b树的主要差别_b树b-树b+树区别

数据结构-B树　　首先从二叉搜索树开始说起。　　二叉搜索树是左<根<右的树，一个关键字分为了两个区间，左边是比根结点小的，右边是比它大的。　　如果将二叉搜索树扩展，每个结点中不再只含一个关键字了，那么就可以将区间分为更多的子区间，这就是B树　　B树，又称多路平衡查找树，B树中所有结点的孩子个数的最大值称为B树的阶，通常用m表示。一棵m阶B树或为空树，或为满足如下特性的m叉树:1）树中每个结点至多有m棵子树，即至多含有m-1个关键字。2）若根结点不是终端结点，则至少有两棵子树。3）除根结点外的所有非叶结点至少有m/2(向上取整）棵子树，即至少含有，m/2-1(向上取整）个关键字4) 所有的叶结点都在最下面一层，叶结点是不带任何信息的。叶结点其实也就是查找失败的结点。5) 终端结点，就是叶子结点上面那一层。终端结点是有数据的，而叶子结点是没有数据的6) 对于每一个节点来说，它的任何一个子数的高度都一定是相同的　　举例说明上述特性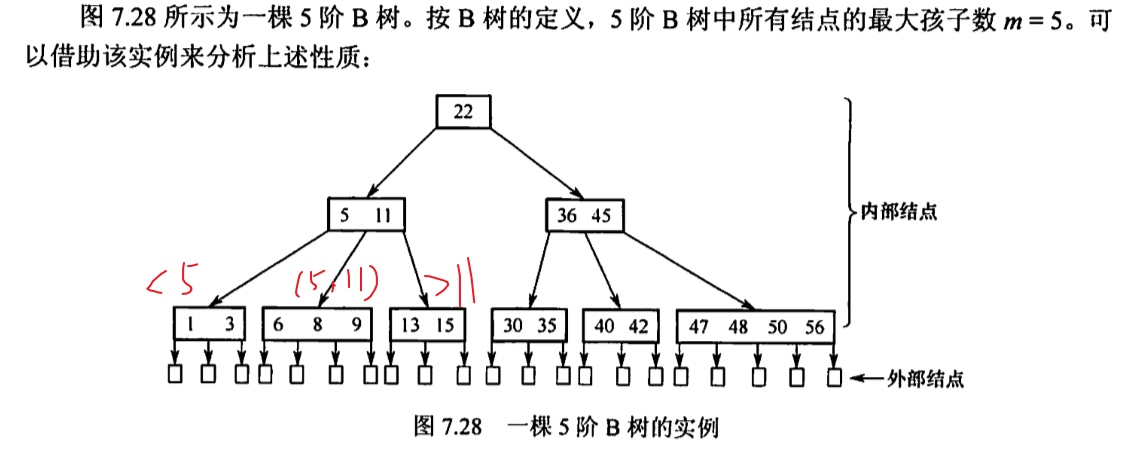

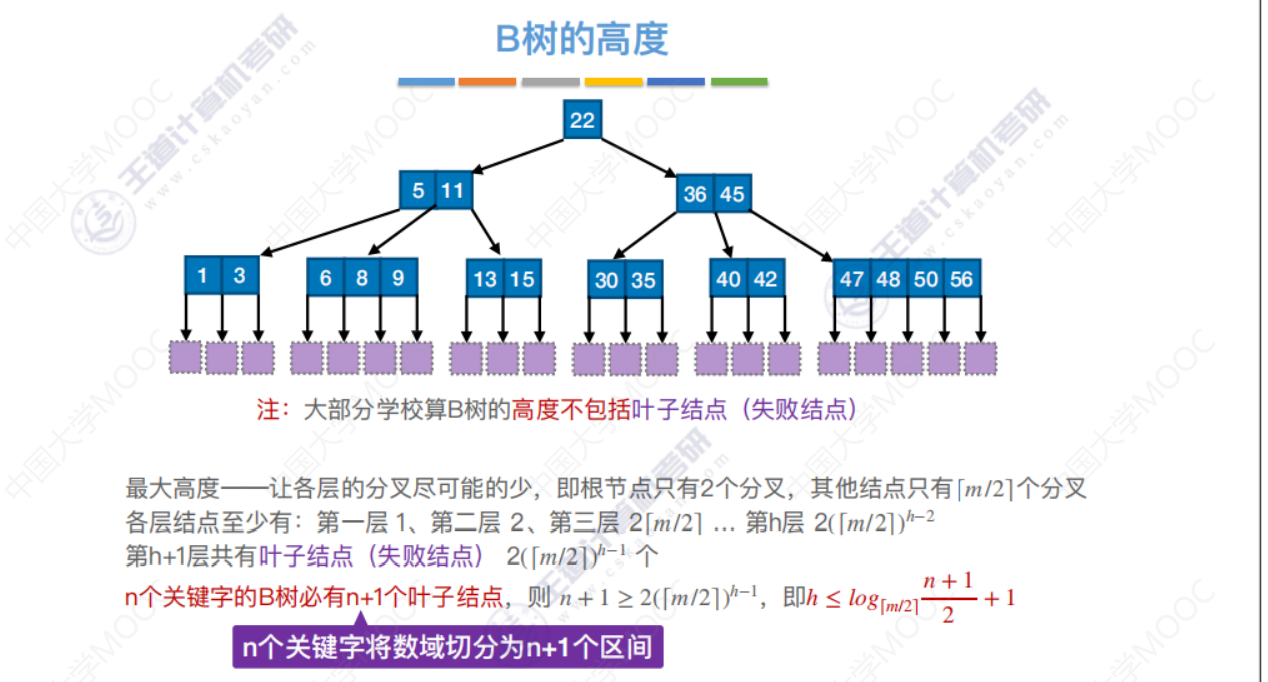
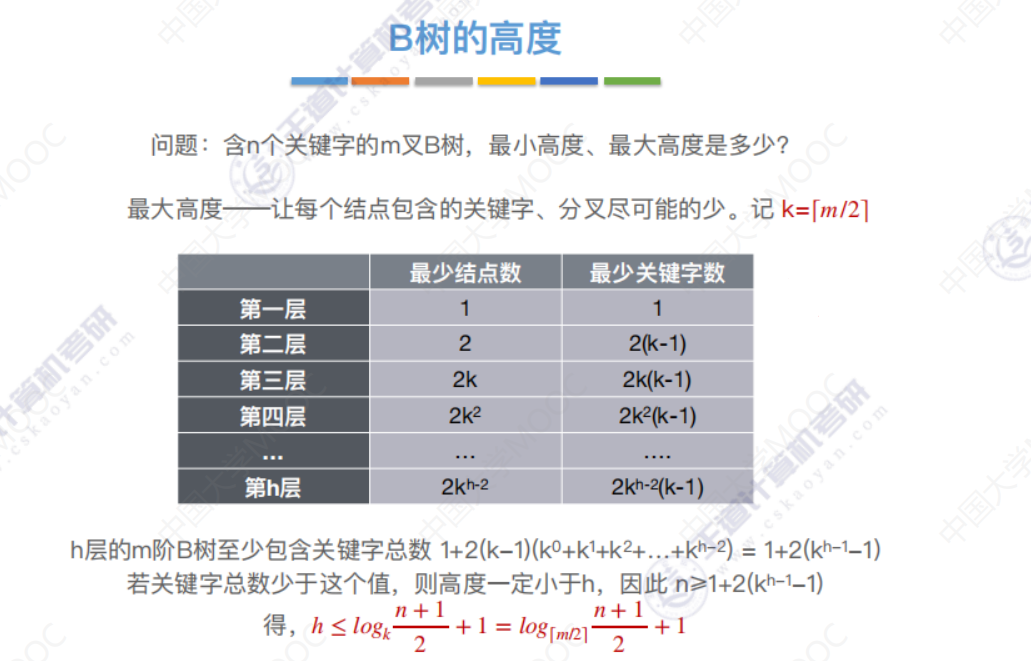
　　1 特性1：　　以左侧第二层结点为例子，非终端结点内含有5，11两个关键字，以这两个关键字为范围划定了三个区间，这就是特性1：树中每个结点至多有m棵子树，即至多含有m-1个关键字。子树要比关键字多1，也就是说，画出来的分叉要比关键字多一个。　　问题1：为什么要对B树的关键字个数进行限制呢？　　答：如果每一个节点当中只保存一个关键字，也就是每个节点只有两个分叉的话，五叉查找数就退化成了二叉查找树？在这种情况下，由于每一个节点当中的关键字数量变少，所以如果说关键字的总数相同的话，那我们的这个树会变得细长瘦高的，就是变高了。查找树越高，在进行查找的时候就需要找更多层的节点，就会导致效率更低。　　所以，为了保证查找树的效率，规定在这个 M 叉查找树当中，除了根节点之外，其他的任何一个节点都至少要有2/m-1(向上取整）个关键字。（如5/2- 1向上取整为2）。这样的规定可以保证五叉查找树每一个节点当中的关键字个数不会太少。那这样就可以保证这棵树不会变得很高，层数不会太多，相应的查找效率也可以得到保证。　　问题2：为什么B树要保持平衡？　　答：为了查找效率。因为B树是需要查找磁盘，层数越高，查找磁盘的次数越多，而访问磁盘是比较慢，比较费时间的，为了保证查找效率，在构建B树的时候，会对其高度进行限制，尽可能地让其保持平衡。　　问题3：怎么保持B树的平衡　　答：回忆下AVL（二叉平衡树）中是这么要求的，左右两棵子树的高度差不超过1，即平衡因子不超过1。对B树而言，高度差不超过1，太难为它了，毕竟有那么多的子树，因此，做出了一个简单粗暴的决定，规定在 m 叉查找树（B树）中，对于任何一个节点，它所有的子树的高度都要相同，就是不能有高度差。那如果能做到这一点，是不是就可以保证我们的这棵多差查找数它是平衡的，也就可以保证它不会有太多层，从而就保证了查找的效率。　　这样平衡的规定也能保证所有的失败结点（叶子结点）都在最下面那一层。　　2 特性2：　　第二个特性，如果根节点它不是终端节点的话，那么它至少会有两棵子树。　　问题4：为什么至少有两棵子树呢？万一只有两个结点呢？　　这个特性其实已经被之前总结的绝对平衡的特性给包含了，因为要保证任何一个节点都绝对平衡。　　所以对于根结点来说，如果它不是终端节点的话，它有没有可能只有左边的这一棵子树呢？这样的话就不能保证根节点的绝对平衡？因此为什么它至少会有两棵子树？就是因为之前提出了一定要保证包括根节点在内所有节点的一个绝对平衡，因此它至少会有两棵子树。　　3 特性3 叶子结点都在最下面　　三种不同的称呼：叶子结点=失败结点=外部结点　　所有的叶子节点都出现在同一层，并且不带信息。　　问题5：为什么说它不带信息呢？　　答：因为这些失败节点其实本质上就是一个空指针。　　问题6：为什么会出现在同一层上呢？　　答：是因为要求所有的节点都绝对平衡，因此所有的叶子节点一定都是同时出现在最下面这一层。　　4 B树的高度　　如果说一棵 m 阶 B 树含有n个关键字，那我们来看一下它的最小高度和最大高度分别是多少？大部分的教材计算 B 树的高度的时候都是不包括叶子节点，也就是不包括最下面的这一层失败节点　　问题7：最小高度可能是多少？　　答：回想下满二叉树，每一层都是满的。对于二叉树有：　　
$n=1+2+2^2+2^3+...2^{h-1}\\=1\times \frac{1-2^{h-1}}{1-2}\\=2^{h-1}-1$ 　　所以高度有：
　　对m叉查找树同理，高度有
　　问题8：最大高度为多少？　　答：要让这棵树长得尽可能的高，那就需要让各层的分叉尽可能的少。所以对于根节点来说，最少可以有两个分叉，而对于其他的节点来说，最少可能会有m/2 向上取整这么多个分叉。所以在分叉最少的情况下，第一层只有一个根节点，第二层会有两个节点，那第三层又会由第二层的这两个节点再分别发出这么多个分叉。所以第三层至少会有 2 乘以m/2 向上取整，就至少会有这么多个节点。

　　为什么是大于呢？　　计算出来的式子，是叶子结点的下限，也就是理想状态下，而n+1是实际状态下。　　计算过程也可参照此表格

　　小结：

　　5 B树的插入　　插入的核心要求就是要能够保证每一个结点的关键字个数处于一个要求的范围，并且任何一个关键字的值都要大于它左边那颗棵子树的值，同时又要小于它右边那棵子树的值。第一步：定位简单说，就是插到哪里去？当插入一个新的素的时候，都是插入在终端节点。至于终端结点插入到哪个位置，根据查找的序列来确定。　　第二步：插入和调整在插入了一个新的关键字之后，有可能会导致此次被插入那个节点的关键字个数超过上限。那这个时候就需要进行分裂的操作，把中间那个素提到父节点当中，然后把原来的节点分为左和右这样的两个部分。如果做了这一步操作之后，导致它的父节点关键字又超过上限。那在这种情况下，我们就需要继续的往上一级进行分裂。直到不产生分裂为止。　　6 B树的删除　　B树的删除分为终端结点和非终端结点。　　删除还会牵涉到：是否会导致B树不符合其定义的情况。比如，删除结点前后，关键字的个数，B树的平衡性有没有遭到破坏　　删除的情况可分为以下三种　　1）关键字的个数够，可以直接删除关键字　　2）关键字不够，但是兄弟够借这种情况下，把兄弟的结点中的一个关键字移上去，把原本父结点中的关键字拿下来。　　3）关键字不够，兄弟也不够借此时需要合并节点。　　原谅我描述无能，请看图：

B树的删除-1

B树的删除-2 　　7 B+树　　考研大纲对B+树，只要求了解其基本概念即可。　　B+树图形如下

　　B树的性质如下　　1）m阶B+树，每个分支结点最多有m棵子树（孩子结点)。2）非叶根结点至少有两棵子树，其他每个分支结点至少有
$\lceil m/2\rceil$ 棵子树。3）结点的子树个数与关键字个数相等。4）所有叶结点包含全部关键字及指向相应记录的指针，叶结点中将关键字按大小顺序排列,并且相邻叶结点按大小顺序相互链接起来。5）所有分支结点(可视为索引的索引）中仅包含它的各个子结点（即下一级的索引块）中关键字的最大值及指向其子结点的指针。　　简单概括即是：　　1）结点有多少个关键字，就会有多少棵子树。2）所有的关键字都会在叶结点中体现。并且叶结点中的关键字都是有序的，换言之，B+树支持顺序查找3）所有分支结点只有其对应索引块中关键字的最大值和指针　　B+树和B树的区别　　

　　最重要的是两点：1，关键字的个数不同2，B+树的非终端节点/分支结点不包含信息，而B树的非终端结点/分支结点是包含信息的

b树和b树的主要差别_b树b-树b+树区别

相关推荐