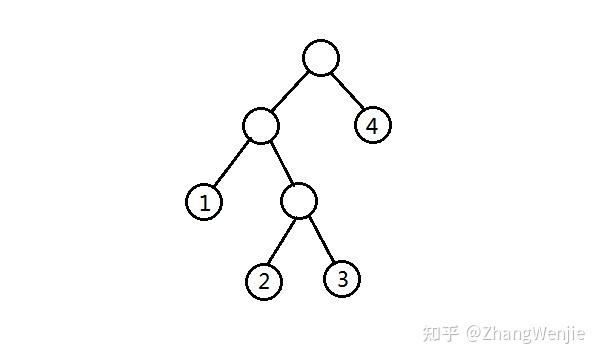
[0x17-148&149][NOIP2004 提高组&NOI2015] 合并果子&荷马史诗【哈夫曼树】 最近过完年了,眼瞅着马上就要开学了,再学此寒假最后一个数据结构好了。 我挑的这个 哈夫曼树 学其实有点波折,一开始我想着直接接着树状数组下去学线段树,但考虑不能囫囵吞枣,仔细一想真咽不下去。然后想着写树状数组关于逆序对的应用,但又感觉没必要花这时间去精心写一个分支的文章。 接着我去翻了翻ccf的大纲,发现 【4】哈夫曼树的定义、构造及其遍历[1] 还不认识。就有了这篇文章。(废话有点多) 哈夫曼树 定义 我们可以通过一个问题作为引子: 假设构造一棵有





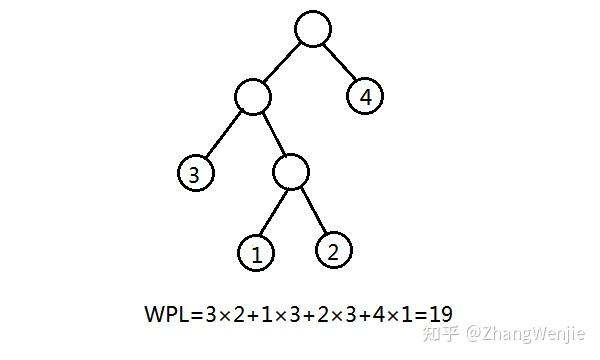




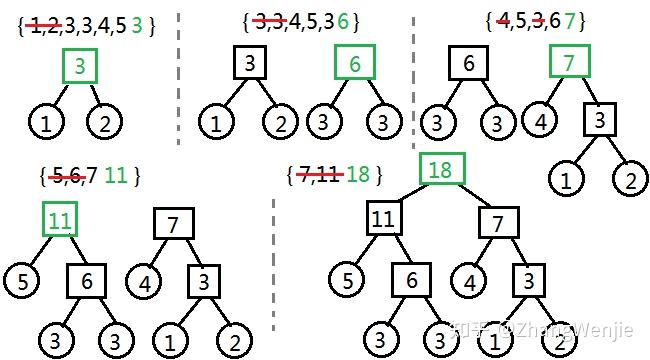

















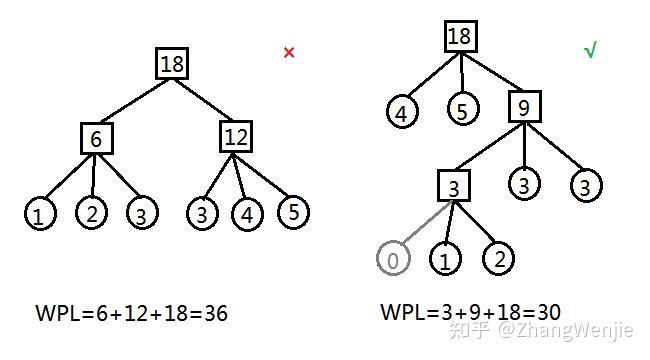





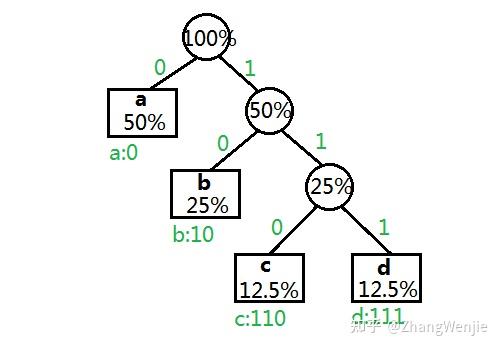













![哈夫曼编码例题与答案_哈夫曼编码例题与答案插图79 [0,k-1]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)





2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/48055.html