二叉平衡排序树怎么构造_最佳二叉排序树是平衡二叉树吗平衡二叉树平衡二叉树是一种二叉排序树,其中每个结点的左子树和右子树的高度差至多等于1。是两位俄罗斯数学家(G.M,Adelons-V.MLandis)共同发明的一种解决平衡二叉树的算法,也称之为AVL
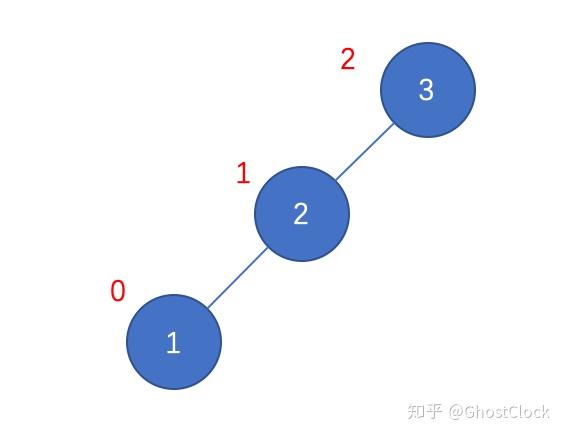
平衡二叉树 平衡二叉树是一种二叉排序树,其中每个结点的左子树和右子树的高度差至多等于1。是两位俄罗斯数学家(G.M,Adelons-V.MLandis)共同发明的一种解决平衡二叉树的算法,也称之为AVL树。 高度平衡:要么是一颗空树,要么它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1;将二叉树上结点的左子树深度减去右子树深度值称之为平衡因子BF(Balance Factor)。 最小不平衡树:距离插入点最近的,且平衡因子的绝对值大于1的结点为根结点的子树。 平衡二叉树构建基本思想:在构建平衡二叉树的过程中,每当插入一个结点时,先检查是否因插入而破坏的平衡性,若是,则找到最小不平衡子树,在保持二叉排序树特性的前提下,调整最小不平衡子树中各结点之间的链接关系,进行相应的旋转,使之称为新的平衡子树。 平衡二叉树构建的模拟: 将数组a[10] = {3,2,1,4,5,6,7,10,9,8}构建二叉排序树。 1.插入结点3,2,1

 插入结点3,2,1 因平衡因子超过了1,需要进行调整
插入结点3,2,1 因平衡因子超过了1,需要进行调整

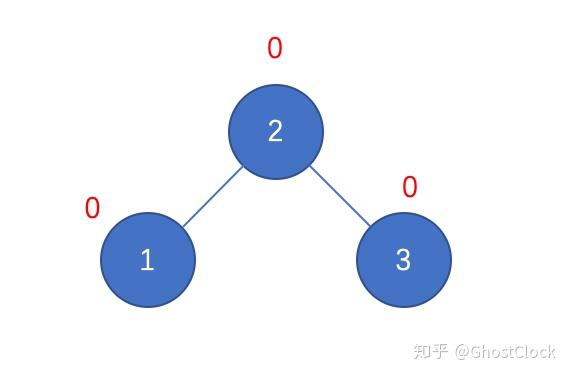
 调整后 2.插入结点4
调整后 2.插入结点4

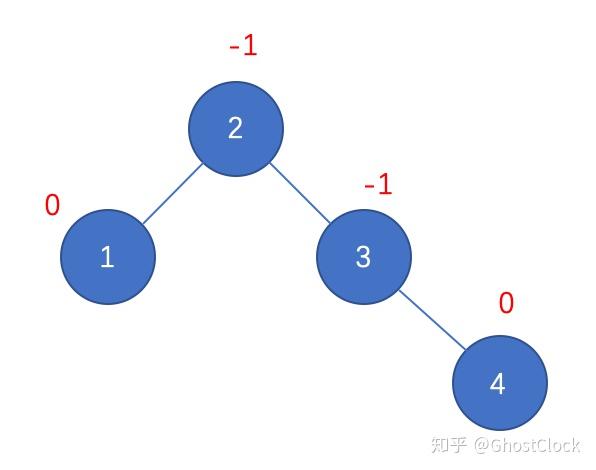
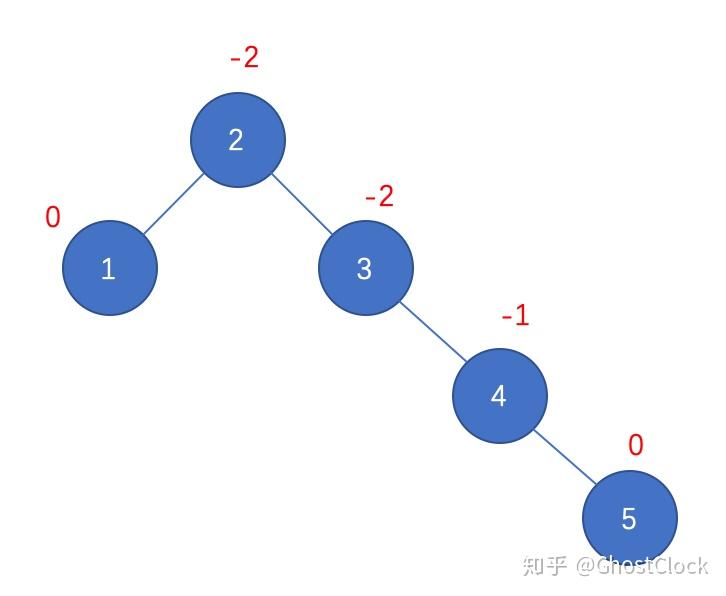
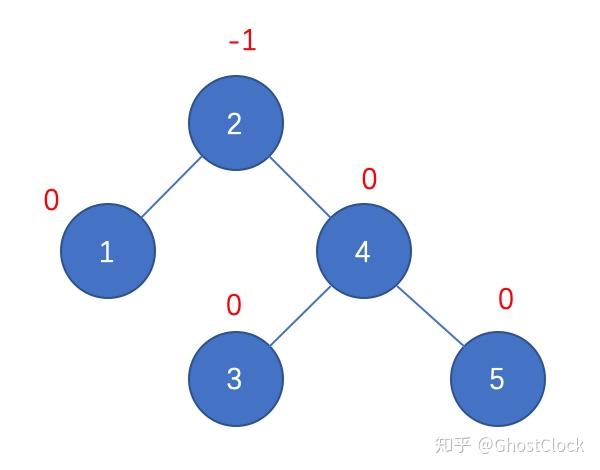
 插入结点4的效果 3.插入结点5
插入结点4的效果 3.插入结点5

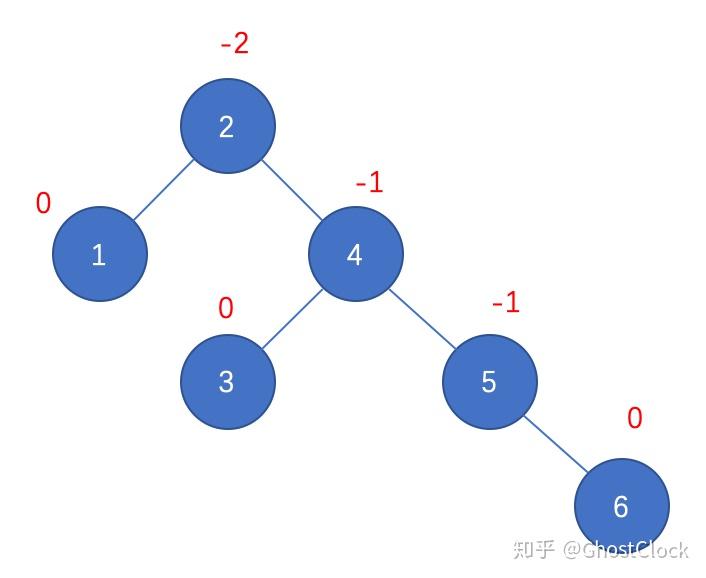
 插入结点5 调整后
插入结点5 调整后

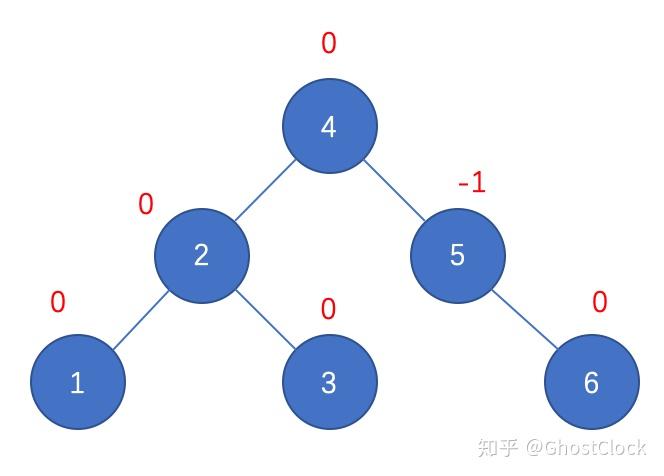
 结点5调整后 4.插入6
结点5调整后 4.插入6

 插入6 调整后
插入6 调整后

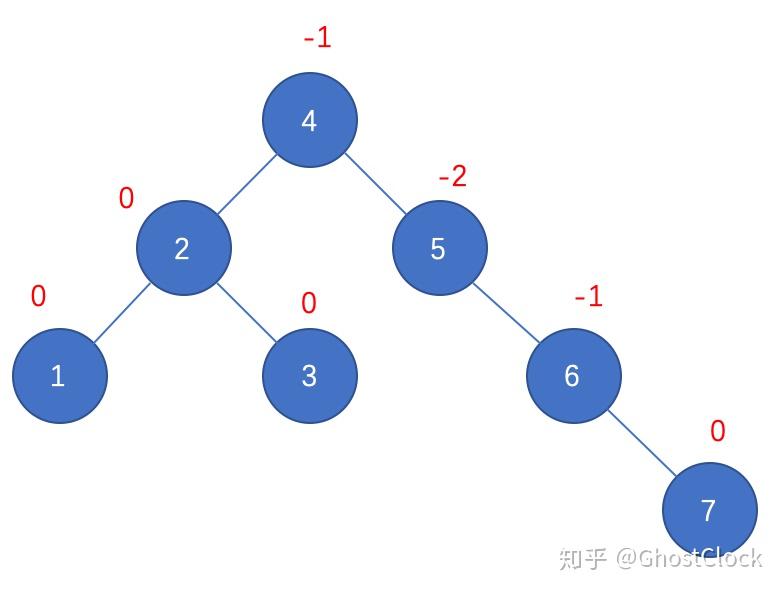
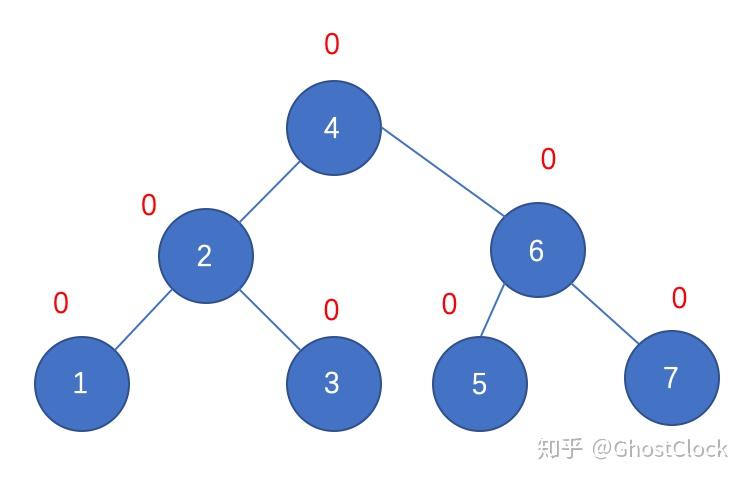
 结点6调整后 5.插入结点7
结点6调整后 5.插入结点7

 插入结点7 调整后
插入结点7 调整后

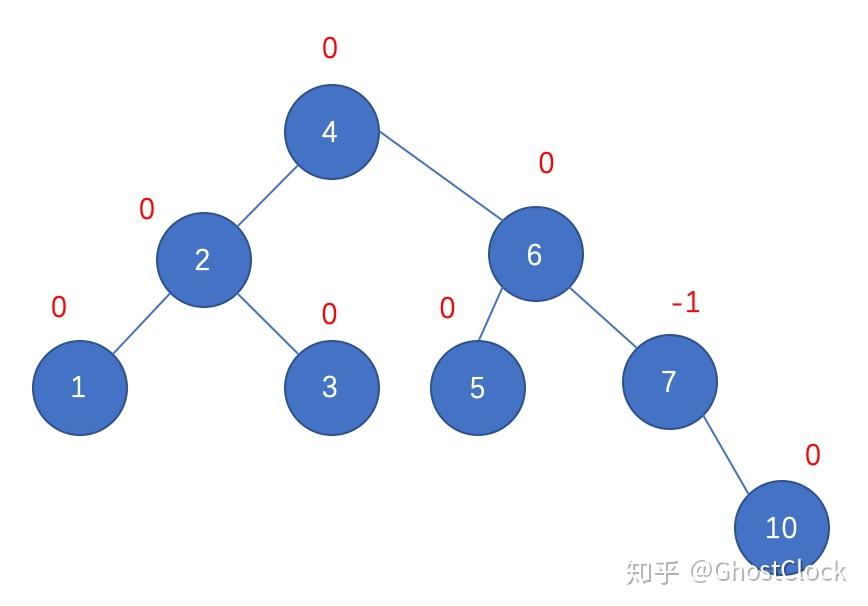
 调整后的结点7 6.插入结点10
调整后的结点7 6.插入结点10

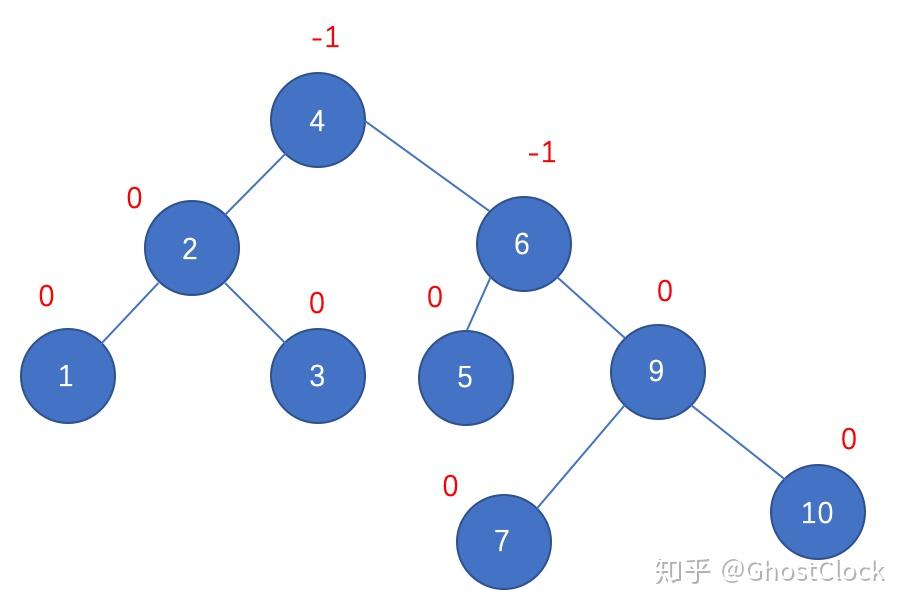
 插入结点10 7.插入结点9
插入结点10 7.插入结点9

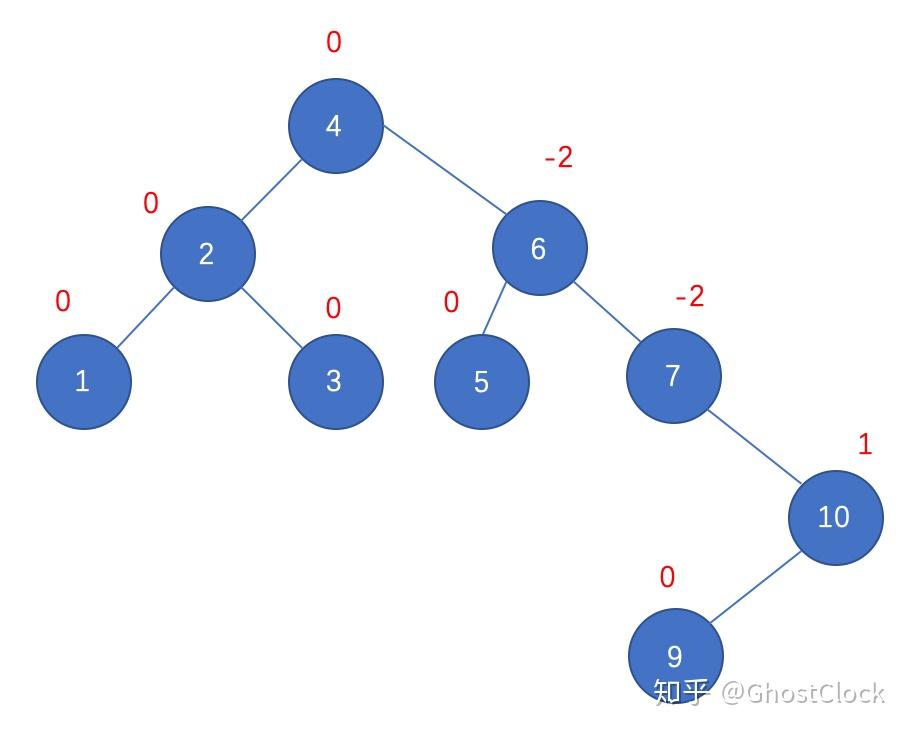
 插入结点9 调整后
插入结点9 调整后

 调整后 但是9比10小不能称为10的右子树
调整后 但是9比10小不能称为10的右子树

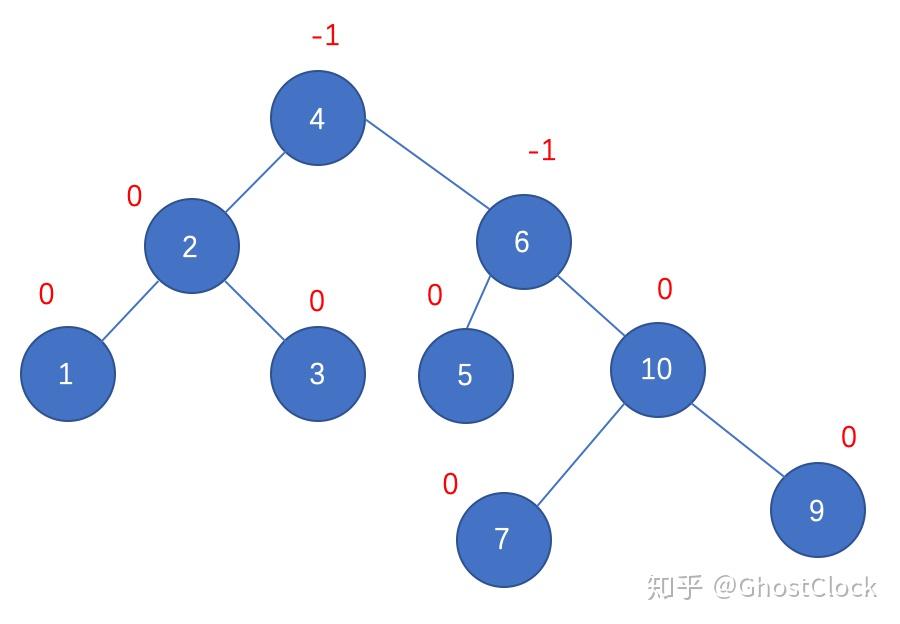
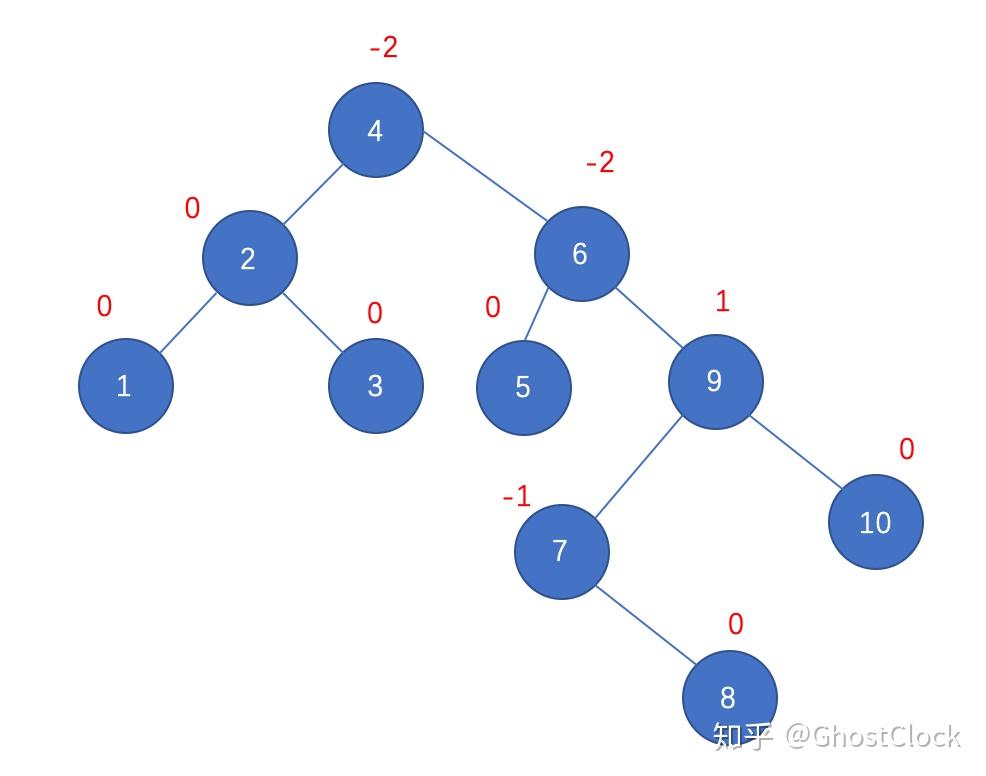
 再次调整后 8.插入结点8
再次调整后 8.插入结点8

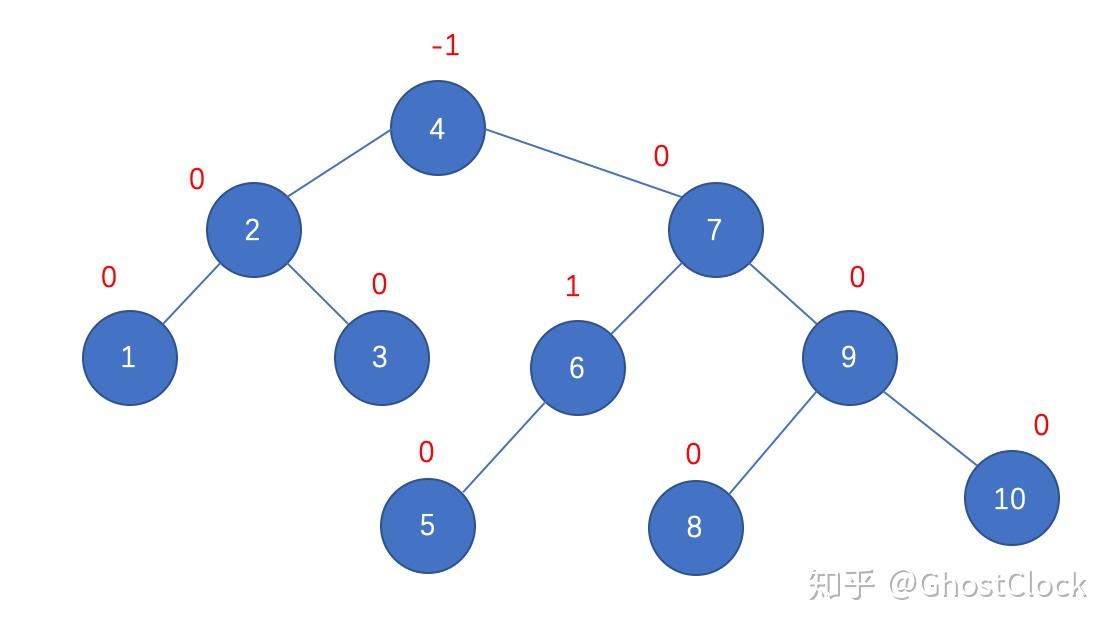
 插入结点8 调整后
插入结点8 调整后

 最后得到的结果 代码实现 创建平衡二叉树 1.定义结点 2.右旋 对以p为根的二叉排序树作右旋处理;处理之后p指向新的树根结点,即旋转处理之前的左子树的根结点; 3.左旋 对以P为根的二叉排序树作左旋处理,处理之后P指向新的树根结点,即旋转处理之前的右子树的根结点 4.平衡⼆叉树结点左平衡旋转 三个常量: 对指针T所指结点为根的二叉树作左平衡旋转处理,算法结束后,指针T指向平衡处理后新的根结点 5.右平衡树失衡处理 对以指针T所指结点为根的二叉树作右平衡旋转处理,本算法结束时,指针T指向新的根结点 平衡二叉树插入实现 若在平衡的二叉排序树T中不存在和e有相同关键字的结点,则插入一个数据素为e的新结点,并返回1,否则返回0。若因插入而使二叉排序树失去平衡,则作平衡旋转处理,布尔变量taller反映T长高与否。 思路:如果T为空时,则创建一个新结点;如果T不为空,判断是否存在相同的结点.如果二叉树中存在相同结点,则不需要插入;如果新结点值e小于T的根结点值,则在T的左子树查找;-如果能在左子树中查找到,则不插入进去.返回False; 如果没有找到,则插入-插入成功taller为TRUE,说明新结点e已经插入进去; 此时需要判断T的平衡因子;-如果平衡因子是1,则说明左子树高于右子树,那么需要调用leftBalance进行左平衡旋转处理;-如果为0或者-1,则说明新插入的结点没有让整颗二叉排序树失去平衡性,只需要修改BF值即可;如果新结点值e大于T的根结点值,则在T的右子树查找;-如果能在右子树中查找到,则不插入进去.返回False; 如果没有找到,则插入-插入成功taller为TRUE,说明新结点e已经插入进去; 此时需要判断T的平衡因子;-如果平衡因子是-1,则说明右子树高于左子树,那么需要调用RightBalance进行右平衡旋转处理;-如果为0或者1,则说明新插入的结点没有让整颗二叉排序树失去平衡性,只需要修改BF值即可; 二叉排序树查找 使用和打印
最后得到的结果 代码实现 创建平衡二叉树 1.定义结点 2.右旋 对以p为根的二叉排序树作右旋处理;处理之后p指向新的树根结点,即旋转处理之前的左子树的根结点; 3.左旋 对以P为根的二叉排序树作左旋处理,处理之后P指向新的树根结点,即旋转处理之前的右子树的根结点 4.平衡⼆叉树结点左平衡旋转 三个常量: 对指针T所指结点为根的二叉树作左平衡旋转处理,算法结束后,指针T指向平衡处理后新的根结点 5.右平衡树失衡处理 对以指针T所指结点为根的二叉树作右平衡旋转处理,本算法结束时,指针T指向新的根结点 平衡二叉树插入实现 若在平衡的二叉排序树T中不存在和e有相同关键字的结点,则插入一个数据素为e的新结点,并返回1,否则返回0。若因插入而使二叉排序树失去平衡,则作平衡旋转处理,布尔变量taller反映T长高与否。 思路:如果T为空时,则创建一个新结点;如果T不为空,判断是否存在相同的结点.如果二叉树中存在相同结点,则不需要插入;如果新结点值e小于T的根结点值,则在T的左子树查找;-如果能在左子树中查找到,则不插入进去.返回False; 如果没有找到,则插入-插入成功taller为TRUE,说明新结点e已经插入进去; 此时需要判断T的平衡因子;-如果平衡因子是1,则说明左子树高于右子树,那么需要调用leftBalance进行左平衡旋转处理;-如果为0或者-1,则说明新插入的结点没有让整颗二叉排序树失去平衡性,只需要修改BF值即可;如果新结点值e大于T的根结点值,则在T的右子树查找;-如果能在右子树中查找到,则不插入进去.返回False; 如果没有找到,则插入-插入成功taller为TRUE,说明新结点e已经插入进去; 此时需要判断T的平衡因子;-如果平衡因子是-1,则说明右子树高于左子树,那么需要调用RightBalance进行右平衡旋转处理;-如果为0或者1,则说明新插入的结点没有让整颗二叉排序树失去平衡性,只需要修改BF值即可; 二叉排序树查找 使用和打印

 平衡二叉树的打印
平衡二叉树的打印
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。
文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/31607.html