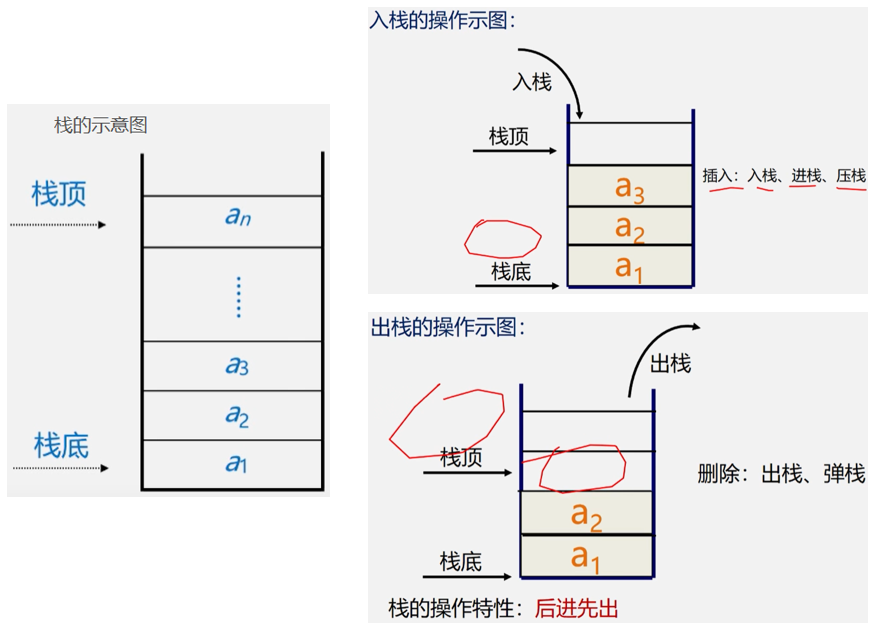
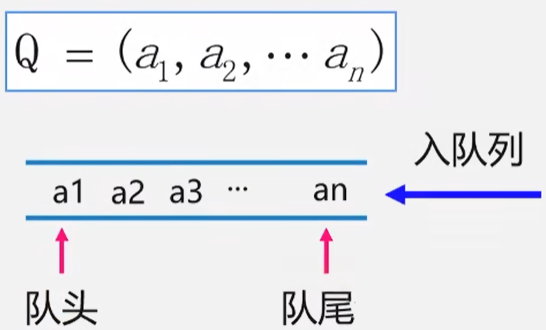
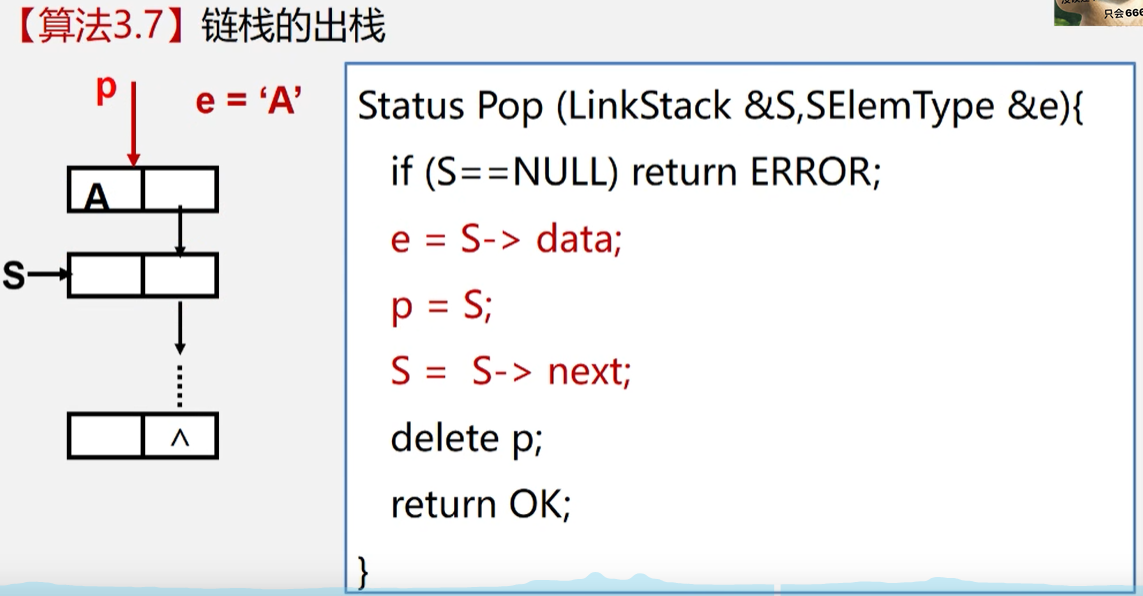
数据结构和算法基础-听课摘抄6-栈和队列-栈 从这一节开始学习新的章节，栈和队列。上节的链接如下：数据的小米虫：数据结构与算法基础-听课摘抄5-线性表的应用、案例分析和实现 栈和队列 1.栈和队列的定义和特点 栈和队列是两种常用的、重要的数据结构，他们也是线性表，是限定插入和删除只能在表的“端点”进行的线性表。在线性表中，插入的位置是
，删除的位置是 。而栈，我们规定，在插入的时候，只能插入在最后一个素，也就是 的位置，在删除时，只能删除最后一个素，也就是第 个位置。栈是后进先出的。在解决问题中，有后进先出的特性，就需要用栈。如数制转换、括号匹配的检验、行编辑程序、迷宫求解、表达式求值、八皇后问题、函数调用和递归调用的实现等问题就可以用栈。
图1 栈(后进先出) 队列，我们规定，在插入的时候，只能插入在最后一个素，也就是 的位置，这与栈式相同的，在删除时，只能删除第一个素，也就是第 个位置，这里与栈是有区别的。队列是先进先出的。在解决问题中，有先进先出的特性，就需要用队列。如脱机打印输出；多用户系统中，多个用户排队分时循环使用CPU和主存；按用户的优先级排成多个队，每个优先级一个队列；实时控制系统中，信号按接受的先后顺序依次处理；网络电文传输，按到达的时间先后顺序依次进行等问题就可以用队列。
图2 队列(先进先出) 栈和队列是线性表的子集，是插入和删除位置受限的线性表。
图3 线性表、栈和队列 栈 栈(stack)又被称为后进先出(Last In First Out)的线性表，简称LIFO结构。栈是仅在表尾进行插入、删除操作的线性表，通常用字母 表示。表尾(即 端)称为栈顶 ，表头(即 端)称为栈底 。插入素到栈顶(即表尾)的操作，称为入栈。从栈顶(即表尾)删除最后一个素的操作，称为出栈。“入”= 压入 = PUSH(x)“出”= 弹出 = POP(y)
图4 栈、入栈和出栈示意图
图5 栈的总结 栈与线性表有什么不同？区别仅仅在于运算规则不同。
图6 栈与线性表区别 队列 队列(queue)是一种先进先出(First In First Out)的线性表，简称FIFO结构。在表一段插入(表尾)，在另一端(表头)删除。通常用字母 表示。
图7 队列示意图
图8 队列的总结 2.栈和队列的案例介绍 本节介绍四个案例，前三个为进制转换、括号匹配的检验、表达式求值和舞伴问题，是栈的案例，最后一个为舞伴问题，是队列的案例。 案例一：进制转换 十进制整数 向其他进制数 (二、八、十六)的转换是计算机实现计算的基本问题。 转换法则：除以 倒取余。该转换法则对应一个简单算法原理： ，其中 表示整除， 表示求余。
图9 进制转换 案例二：括号匹配的检验 
图10 括号匹配的检验 可以利用一个栈结构保存每个出现的左括号，当遇到右括号时，从栈中弹出左括号，检验匹配情况。在检验过程中，若遇到以下情况之一，就可得出括号不匹配的结论。当遇到某一个右括号时，栈已空，说明到目前为止，右括号多于左括号；从栈中弹出的左括号与当前检验的右括号类型不同，说明出现了括号交叉的情况；算术表达式输入完毕，但栈中还有没有匹配的左括号，说明左括号多于右括号； 案例三：表达式求值 表达式求值是程序设计语言编译中一个最基本的问题，它的实现需要用到栈。这里介绍的算法是由运算符优先级确定运算顺序的对表达式求值算法——算符优先算法。
图11 表达式的组成
图12 表达式求值的思想 这个算法整个过程实际较为复杂。 案例四：舞伴问题 假设在舞会上，男士和女士各自排成一队。舞会开始时，依次从男队和女队的队头各出一人配成舞伴。如果两队初始人数不相同，则较长的那一队中未配对者等待下一轮舞曲。现要求写一算法模拟上述舞伴配对问题。 显然，先入队的男士或女士先出队配成舞伴。因此该问题具有典型的先进先出特性，可以用队列作为算法的数据结构。 3.栈的表示和操作的实现 首先是栈的抽象数据类型的类型定义，素可以为0，称为空栈。数据关系还是前趋后继关系，只不过约定了栈顶和栈底。基本操作包括初始化、进栈、出栈、取栈顶素等 。
图13 栈的抽象数据类型的类型定义 然后对栈抽象数据类型中的基本操作进行说明。初始化操作(InitStack)—操作结果：构造一个空栈 ；销毁栈操作(DestroyStack)—初始条件：栈 已存在；—操作结果：栈 被销毁；判断是否为空栈(StackEmpty)—初始条件：栈 已存在；—操作结果：若栈 为空栈，则返回TRUE，否则FALSE；求栈的长度(StackLength)—初始条件：栈 已存在；—操作结果：返回 的素个数，即栈的长度；取栈顶素(GetTop)—初始条件：栈 已存在且非空；—操作结果：用 返回 的栈顶素；栈置空操作(ClearStack)—初始条件：栈 已存在；—操作结果：将 清为空栈；入栈操作(Push)—初始条件：栈 已存在；—操作结果：插入素 为新的栈顶素；出栈操作(Pop)—初始条件：栈 已存在且非空；—操作结果：删除 的栈顶素 ，并用 返回其值； 由于栈本身就是线性表，于是栈也有顺序存储和链式存储两种实现方式，栈的顺序存储(顺序栈)，栈的链式存储(链栈)。下面分别介绍这两种方式。 一、栈的顺序存储(顺序栈) 
图14 顺序栈
图15 顺序表 使用数组作为顺序栈存储方式的特点：简单、方便但易产生溢出(数组大小固定)。上溢(overflow)：栈已经满，又要压入素；下溢(underflow)：栈已经空，还要弹出素； 上溢是一种错误，使问题的处理无法进行；而下溢一般认为是一种结束条件，即问题处理结束。
图16 顺序栈表示 两个指针指向同一个数组，此时相减，得出的结果是两素之间相差几个素。 下面展示顺序栈的一些基本操作： 1.顺序栈的初始化：
图17 顺序栈的初始化 2.顺序栈判断是否为空：
图18 顺序栈判断是否为空 3.求顺序栈长度
图19 求顺序栈长度 4.清空顺序栈
图20 清空顺序栈 5.销毁顺序栈
图21 销毁顺序栈 ★6.顺序栈的入栈
图22 顺序栈的入栈 ★7.顺序栈的出栈
图23 顺序栈出栈 二、栈的链式存储(链栈) 
图24 链栈的表示 链栈的头指针就是栈顶，每一项的next域指向前一结点。 下面展示链栈的一些基本操作： 1.链栈的初始化：
图25 链栈的初始化 2.判断链栈是否为空：
图26 判断链栈是否为空 3.链栈的入栈：
图27 链栈的入栈 4.链栈的出栈：
图28 链栈的出栈 入栈和出栈都很简单，因为只是对最后一个素的操作。 5.取出栈顶素：
图29 取出栈顶素 4.栈与递归 首先对递归做定义：若一个对象部分地包含它自己，或者它自己给自己定义，则称这个对象是递归的；若一个过程直接或间接地调用自己，则称这个过程是递归的过程； 例如，递归求n的阶乘，这就是递归的例子。通常，递归定义的数学函数(如阶乘函数、2阶Fabonaci数列)、具有递归特性的数据结构(如二叉树、广义表)、和可递归求解问题(如迷宫问题、Hanoi问题)，这三种情况常常用到递归方法。 递归问题可以使用分治法求解。分治法对于较为复杂的问题，能够分解成几个相对简单且解法相同或类似的子问题来求解。分治法的使用有三个条件：能将一个问题转变成一个新问题，而新问题与原问题的解法相同或类同，不同的仅是处理的对象，且这些处理对象是变化有规律的；可以通过上述转化而使问题简化；必须有一个明确的递归出口，或称递归的边界；
图30 分治法求解递归问题 我们首先复习一下函数调用时候的顺序。
图31 函数调用的过程 当多个函数构成嵌套调用时，遵循后调用的先返回。与栈的原理相同。那么我们在求解递归问题时，最后调用的最先返回，最先调用的最后返回。
图32 求阶乘的过程
图33 递归函数调用的实现 实现递归函数，就会用到栈。
图34 递归的优缺点递归程序在执行时需要系统提供栈来实现；仿照递归算法执行过程中递归工作栈的状态变化可写出相应的非递归程序；改写后的非递归算法与原来的递归算法相比，结构不够清晰，可读性较差，有的还需要经过一系列优化；
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/31163.html
