二阶巴特沃斯高低通滤波器系数计算 概述 二阶巴特沃斯滤波器是一种常用的信号处理工具。可用于滤除高频噪声,保留低频信号。该滤波器具有瓶阀的频率响应和较好的相位特性,被广泛应用于音频处理、图像处理、通信系统等领域。 二阶巴特沃斯滤波的设计基于巴特沃斯滤波器原理,巴特沃斯滤波器是指在通频带内响应平坦的滤波器。二阶巴特沃斯低通滤波器的特点是在截止频率处有较为平缓的过渡带,可以有效地滤除高频噪声,同时保留低频信号。 巴特沃斯滤波器的设计过程需要确定两个关键参数:截止频率和阶数。截止频率是指滤波器开始衰减的频率,阶数是指滤波器的阶次,决定了滤波器的陡度。在二阶巴特沃斯低通滤波器中,阶数为2,因此可以实现较为陡峭的滤波器特性。 设计二阶巴特沃斯低通滤波器的步骤如下: 1. 确定截止频率:根据实际应用需求和信号特性,旋转适当的截止频率。截止频率是滤波器响应的开始下降的频率,通常以赫兹(HZ)为单位。 2. 计算滤波器参数:根据截止频率和采样频率,计算滤波器的一些关键参数,如角频率、Q值等。角频率是指滤波器的截止频率与采样频率的比值,Q值是值滤波器的品质因数,决定了滤波器的频率响应特性。 3. 设计滤波器传递函数:利用巴特沃斯滤波器的传递函数公式,根据计算得到的参数,确定滤波器的传递函数。传递函数描述了输入信号与输出信号之间的关系,可以用于计算滤波器的频率响应和相位特性。 4. 实现滤波器:利用计算得到的传递函数,可以进行滤波器的实现。常见实现方式包括巴特沃斯滤波器电路、数字滤波器算法等。 5. 验证滤波效果:在设计完成后,需要对滤波器的性能进行验证。可以通过输入不同频率的测试信号,观测输出信号频率特性和相位特性,以验证滤波器的工作是否符合设计要求。 二阶巴特沃斯滤波器特点: 1. 平滑的频率响应、较好的相位特性和较高的滤波器效果。 2. 滤波器阶数较低,难以实现非常陡峭的滤波特性。 3.设计过程中需要权衡截止频率和滤波器的阶数,以达到滤波器效果和计算复杂度之间的平衡。 4.常用信号处理工具,在音频、图像和通信等领域有广泛的应用。通过合理的设计和实现,可以实现对高频 噪声的滤除,保留低频信号,从而提升信号质量和系统性能。 计算二阶巴特沃斯低通滤波器的系数 使用 采样频率:10kHz截止频率:1kHz 如何实际计算下面的差分方程的系数? 知道差分方程将采用这种形式,但不知道如何实际算出系数b0,b1,b2,a1,a2的数字。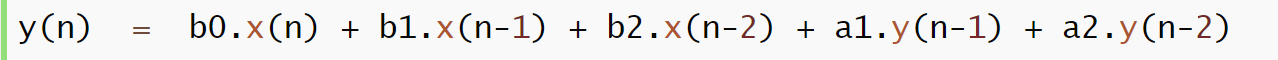
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/26457.html