为什么红黑树效率高_红树林生长周期

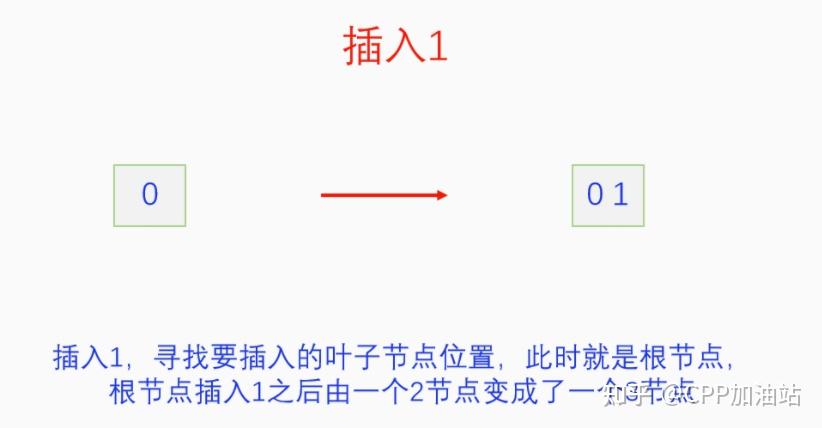
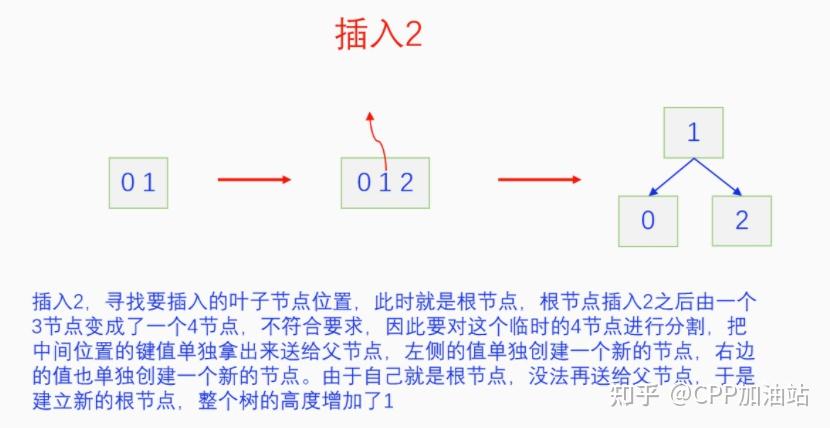
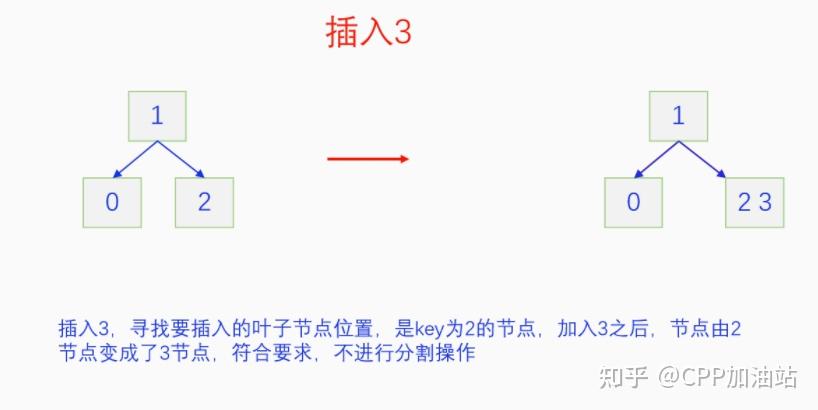
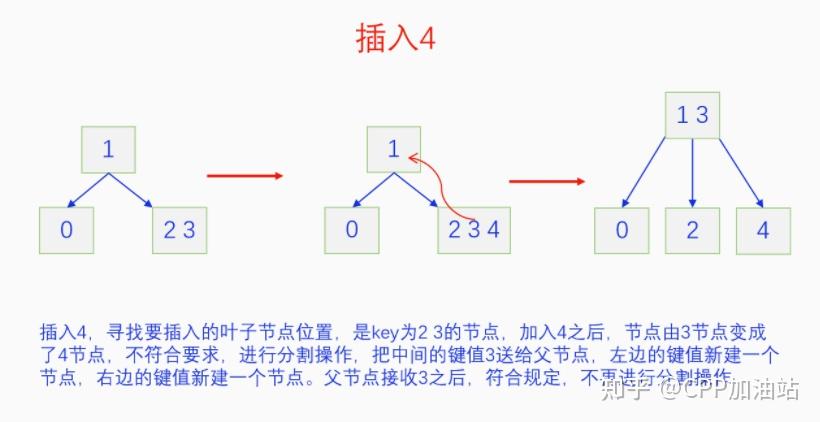
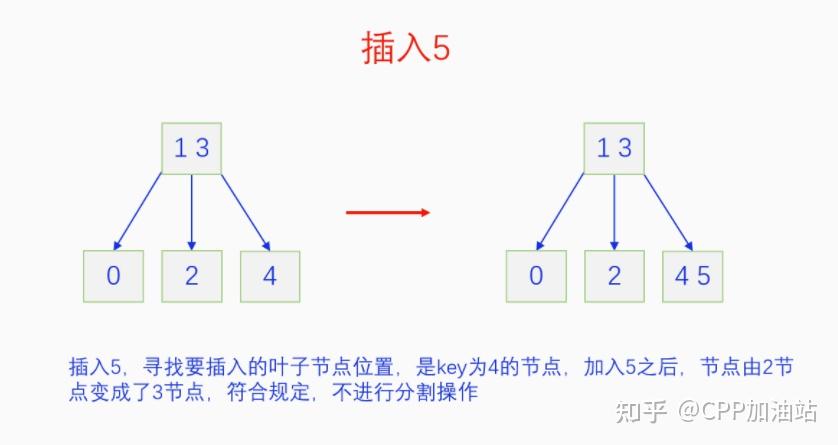
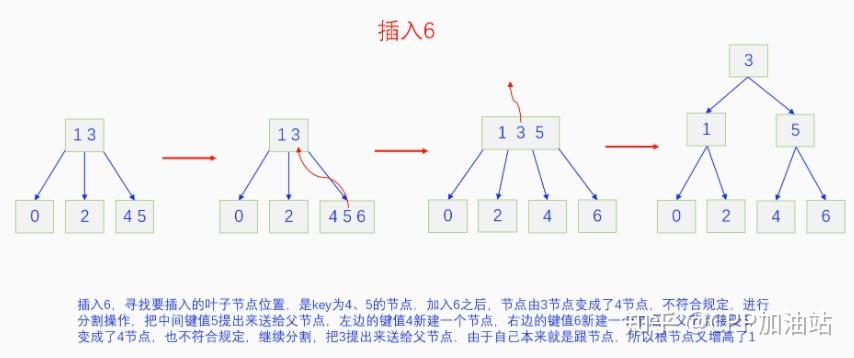
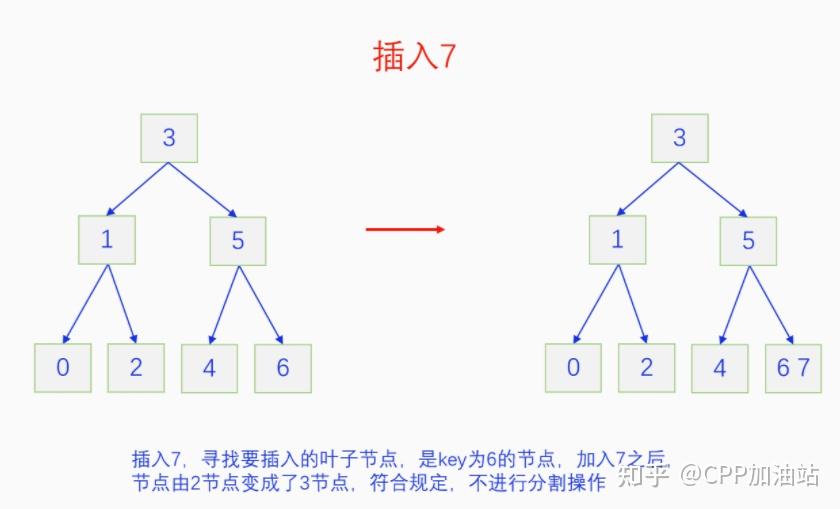
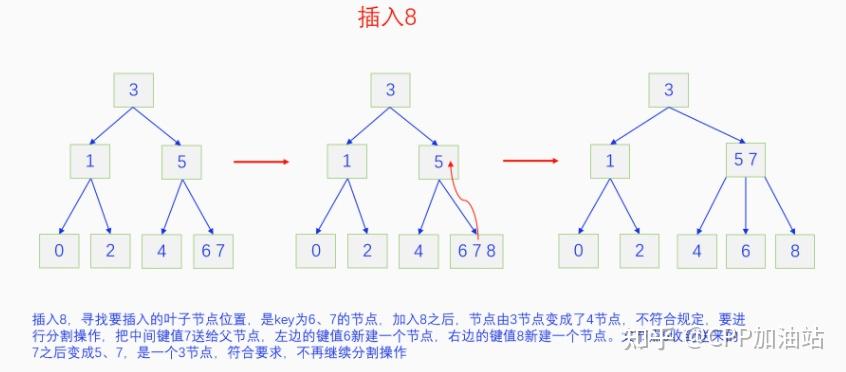
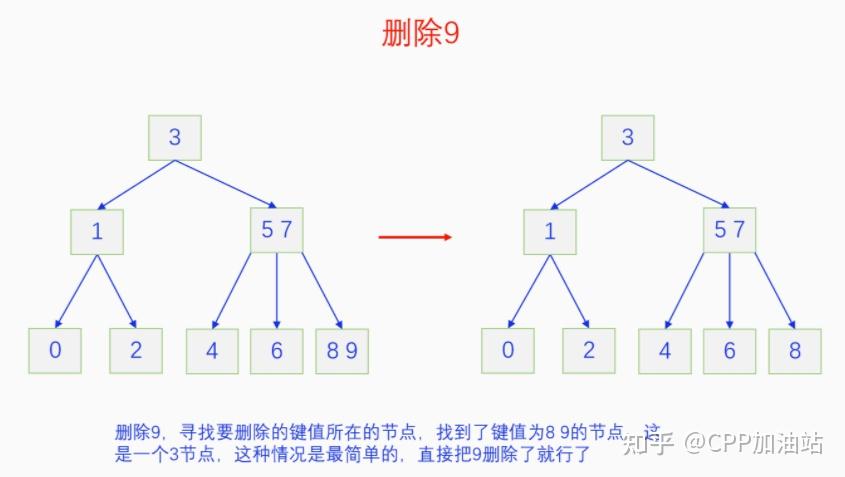
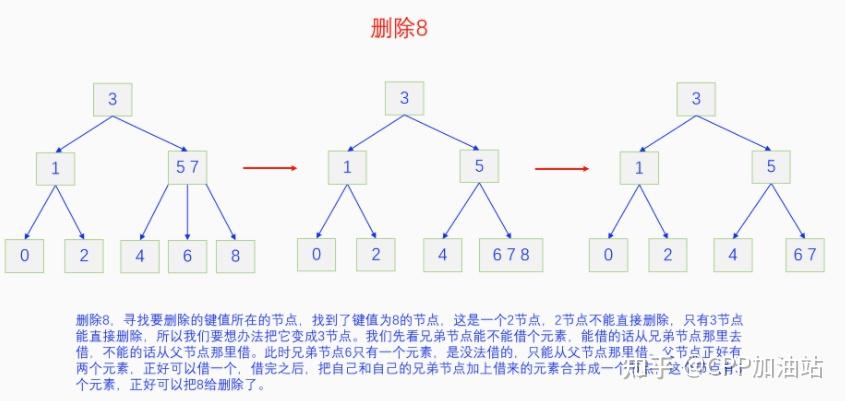
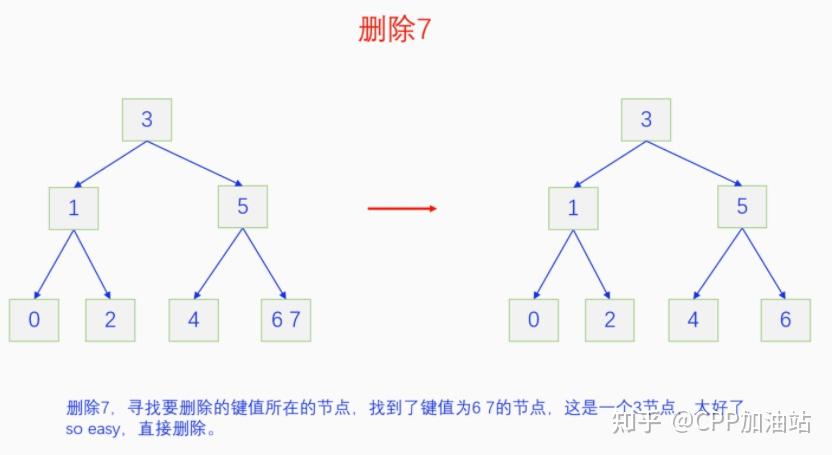
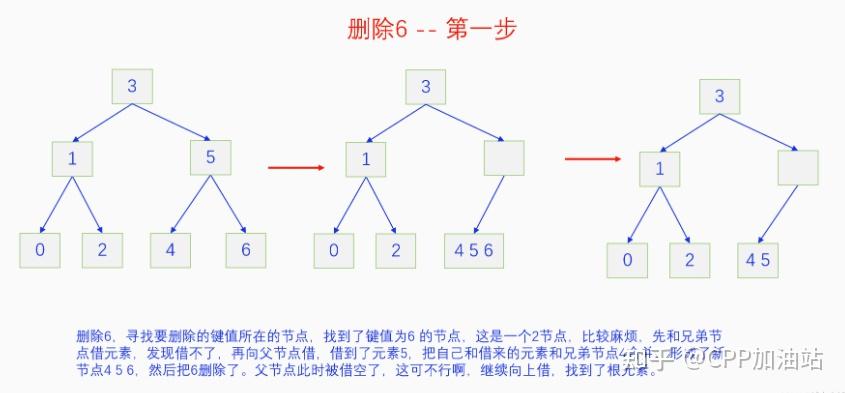
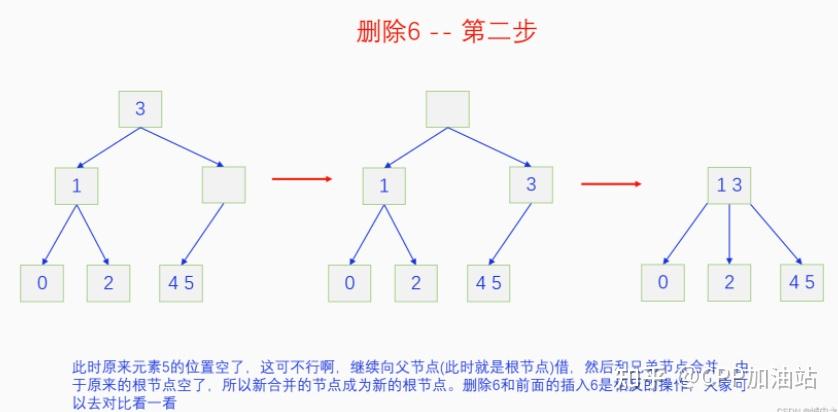
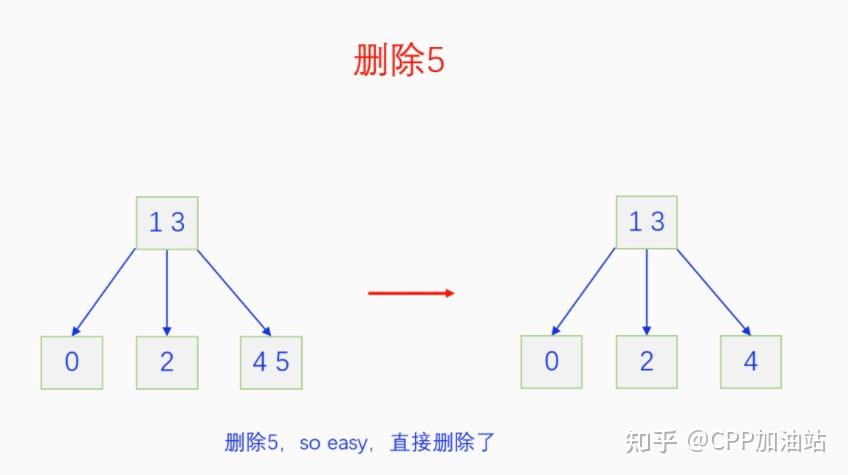
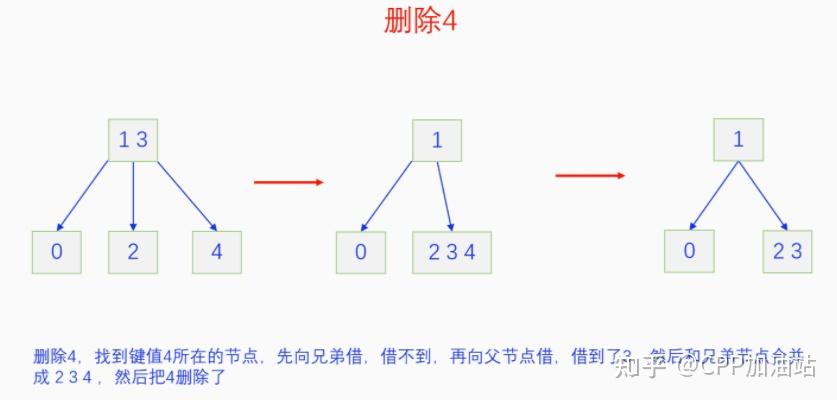
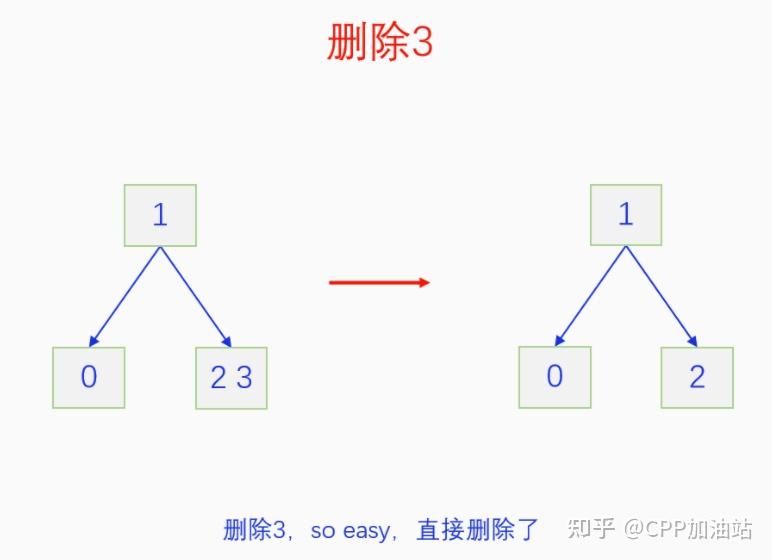
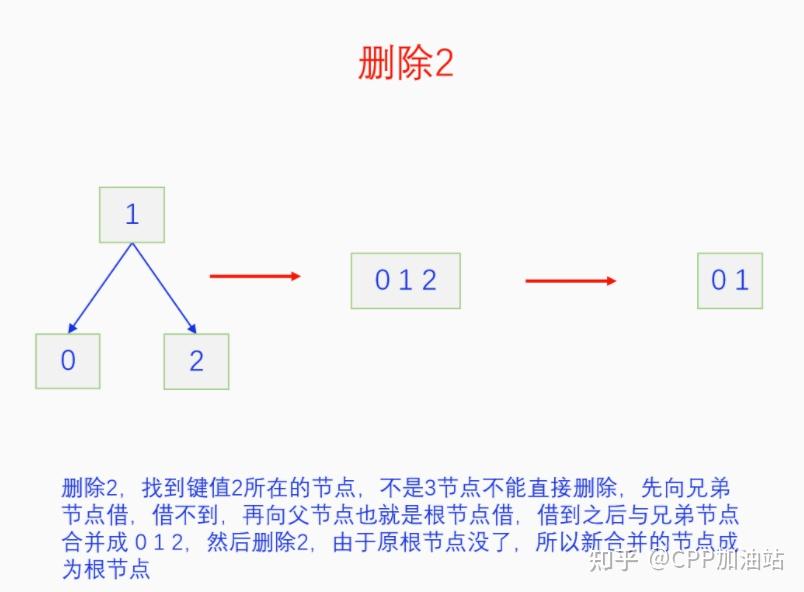
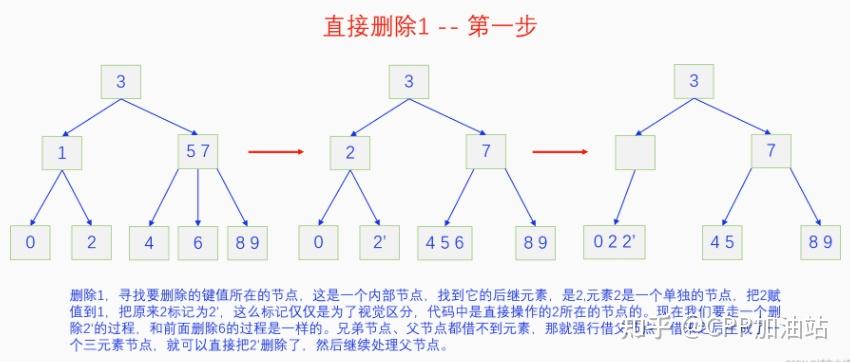
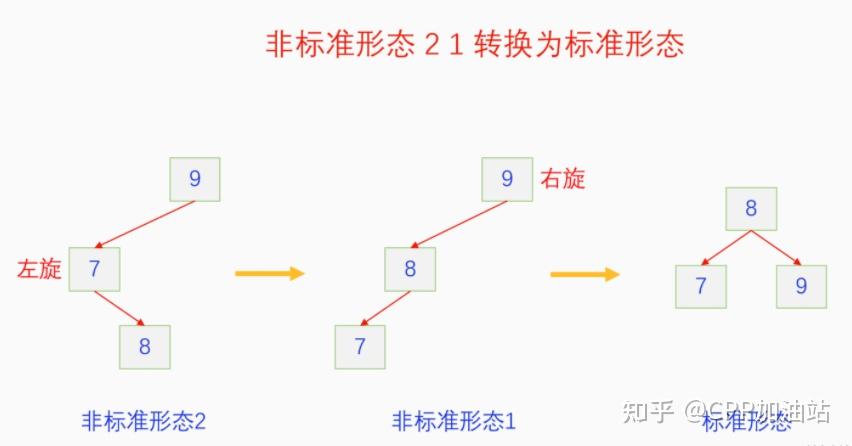
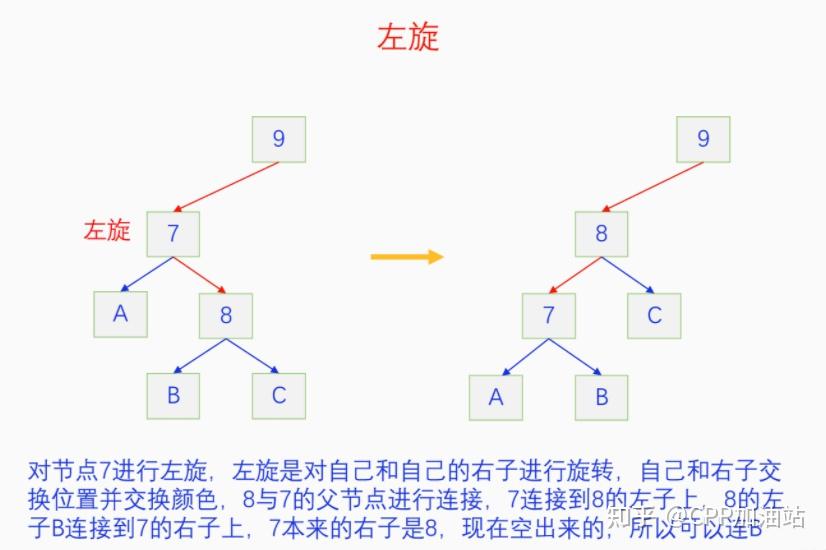
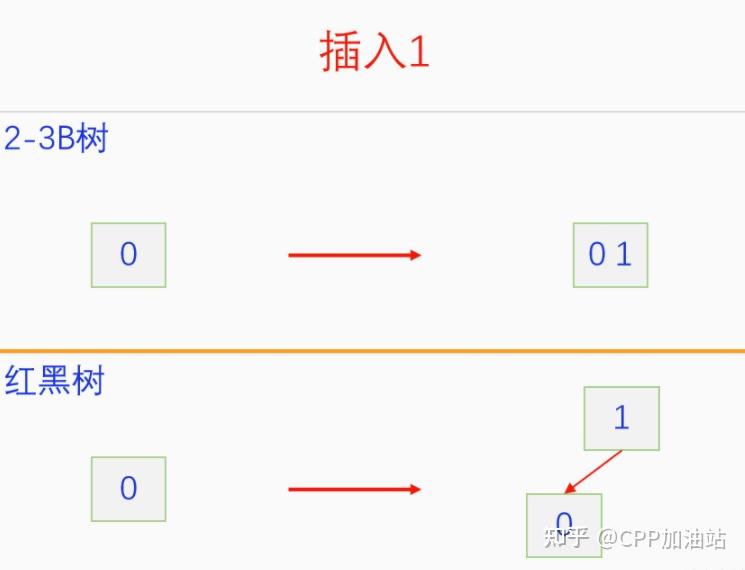
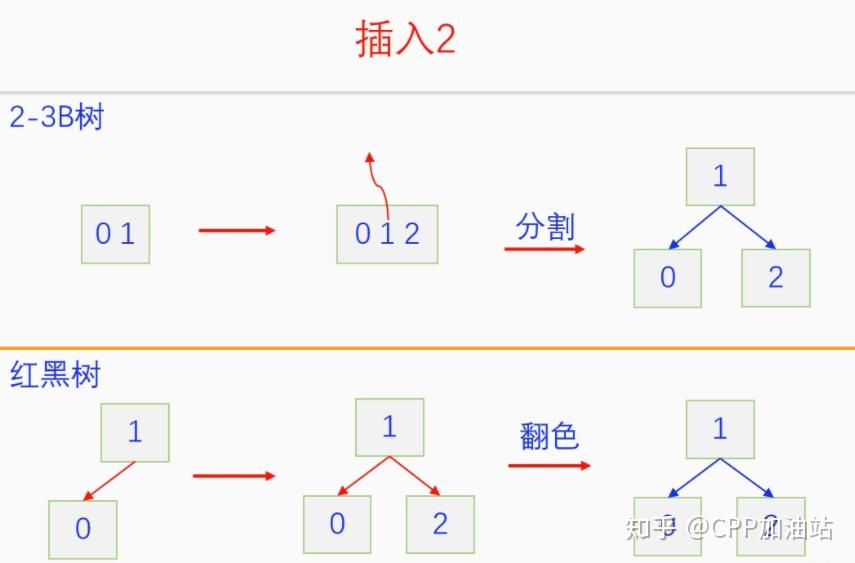
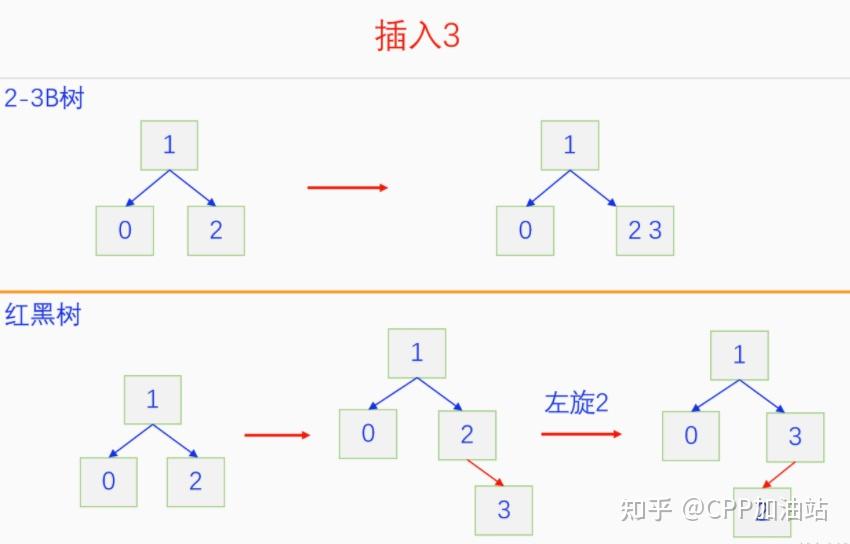
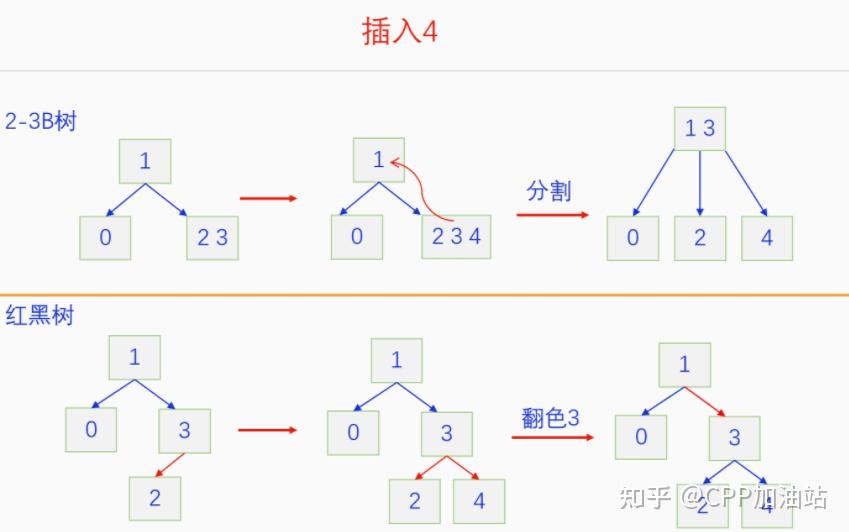
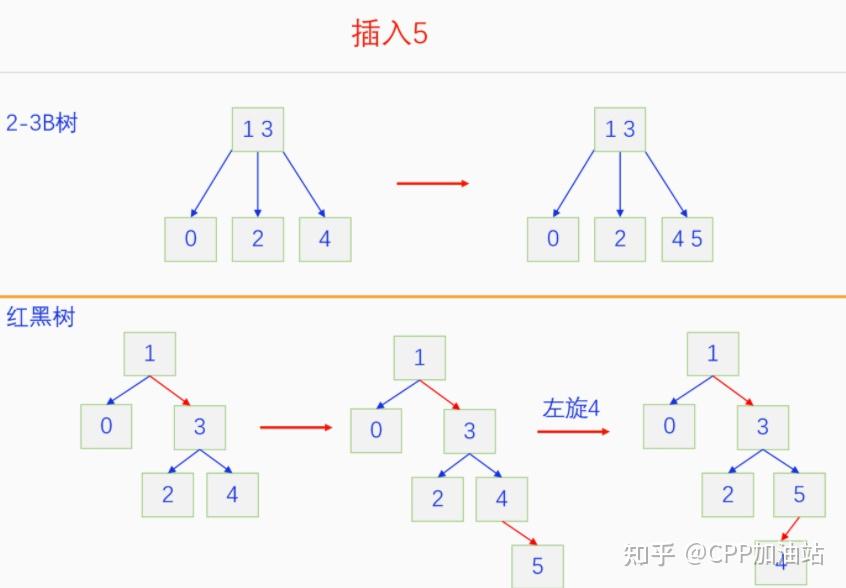
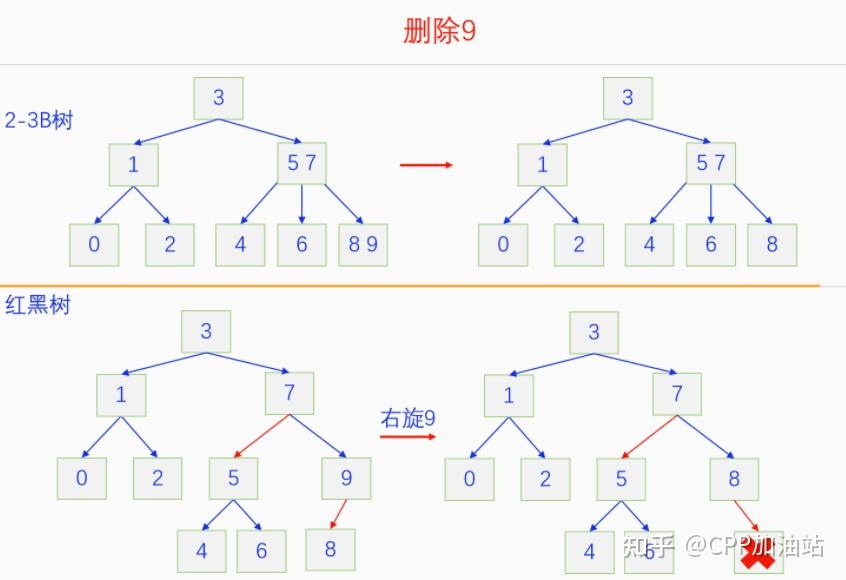
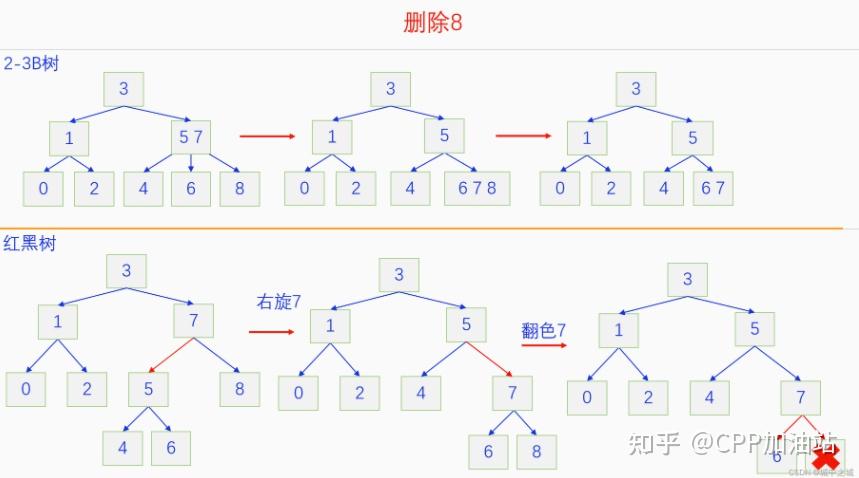
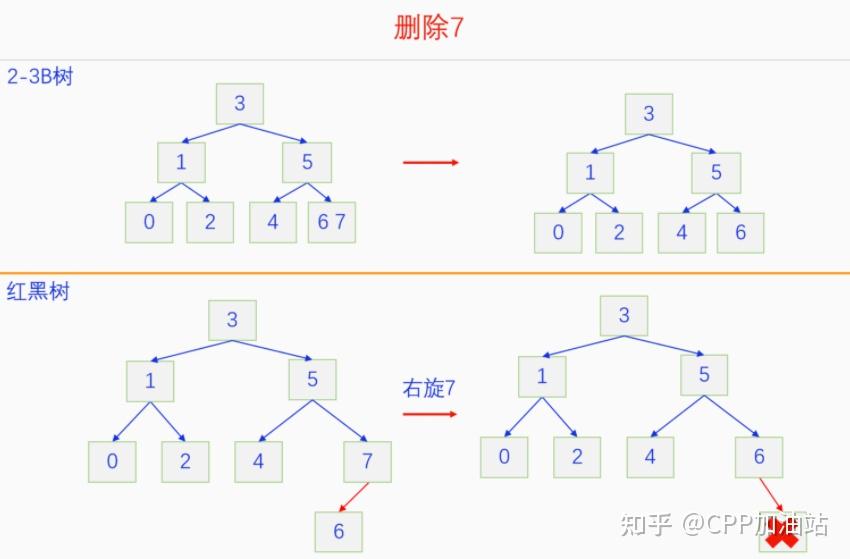
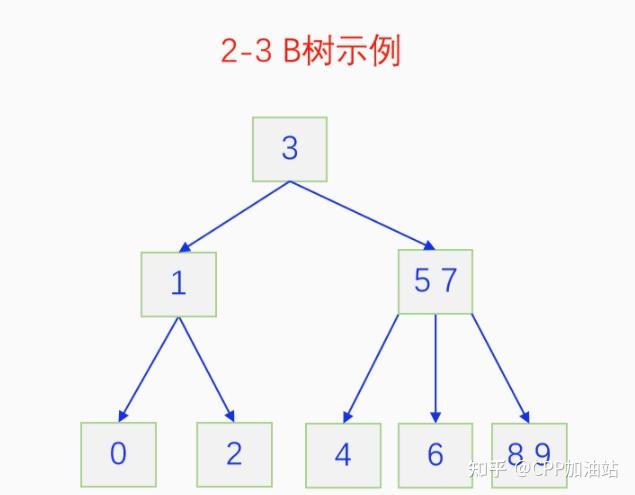
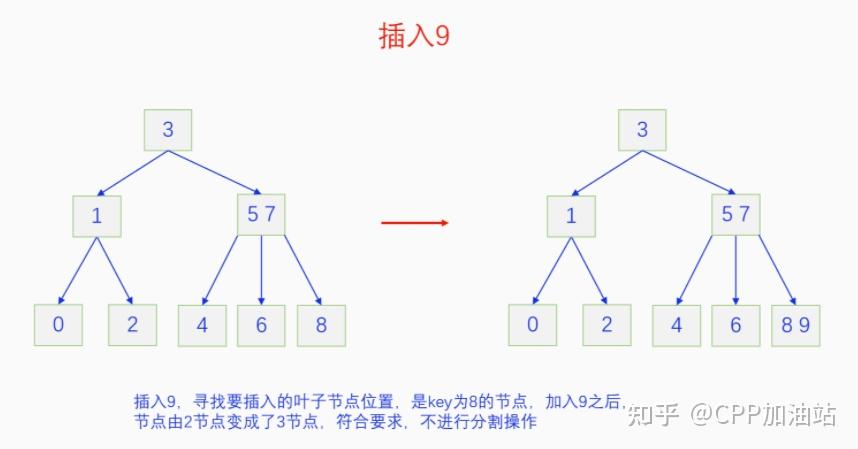
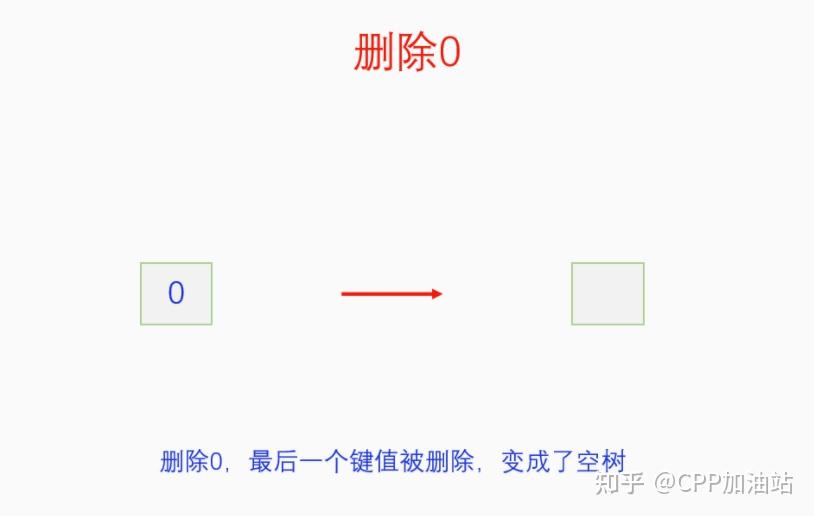
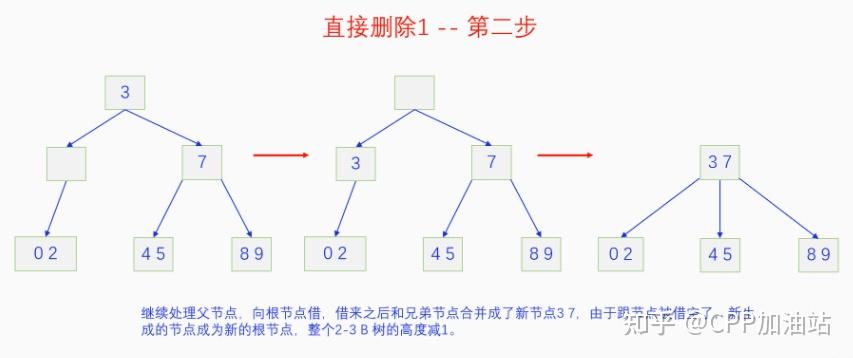
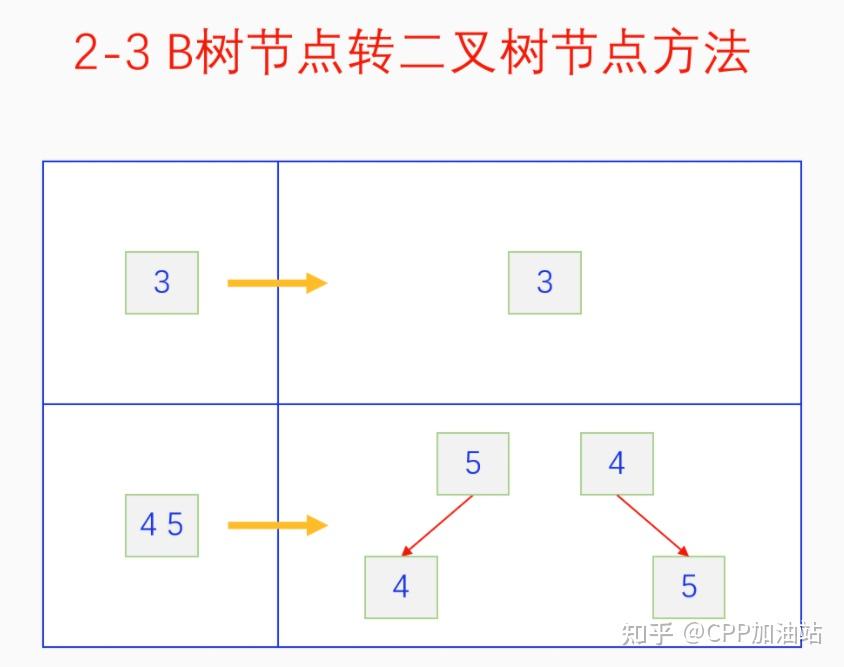
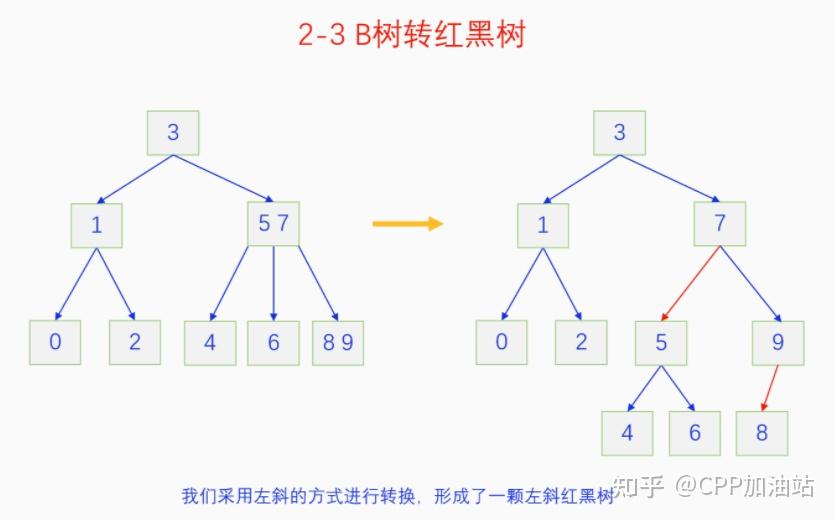
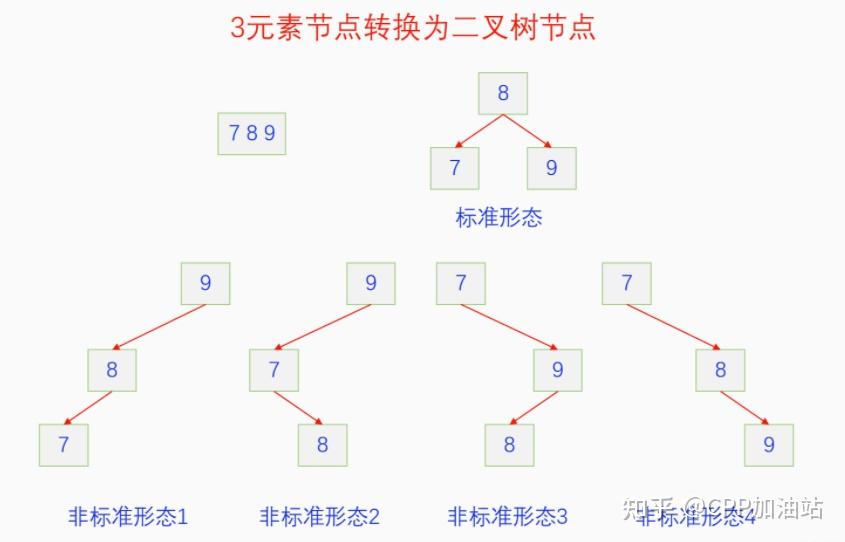
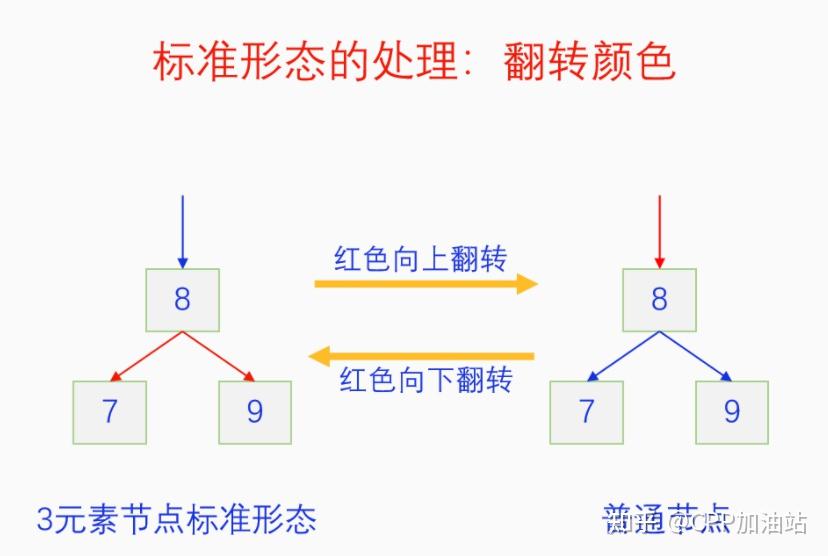
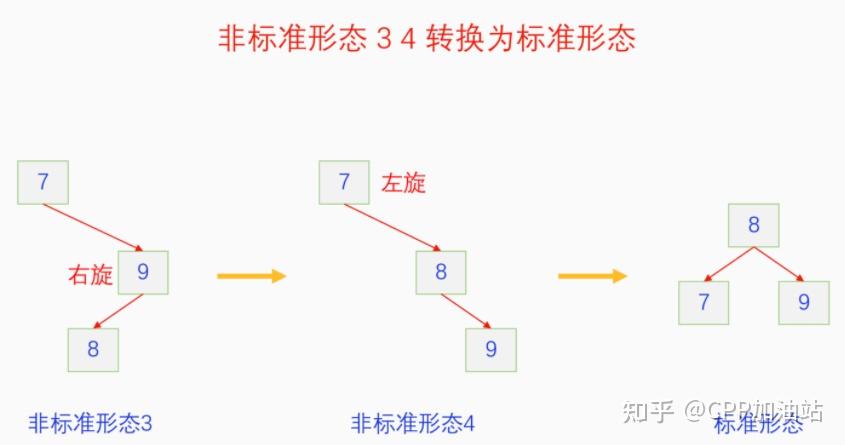
图文并茂丨深入理解红黑树 　　一、红黑树的底层逻辑 　　大家都听说过红黑树，也都知道红黑树很厉害，是计算机里面评价非常高的数据结构。但是每当想学习红黑树的时候，却总是找不到通俗易懂很好理解的学习资料。很多书上上来就是红黑树的定义，然后就是红黑树的实现，直接就把人给整晕了。光看红黑树的定义就有5条，为什么要有5条定义，为什么要这么定义，这么定义是什么意思，光定义都让人懵了，更别说实现了。我看最近抖音上有很多人在讲底层逻辑，只要你掌握了底层逻辑，其它的问题都不在话下，今天我们也来讲一讲红黑树的底层逻辑。在讲之前我们先介绍一下红黑树的诞生，红黑树是Rudolf Bayer在1972年首先提出来的，不过当时并不叫红黑树，而是叫对称二叉 B 树(symmetric binary B-trees)。后来在1978年Leo J. Guibas 和 Robert Sedgewick 对此数据结构进行了修改和完善，并重新命名为红黑树。为什么叫红黑树呢？有两种说法，因为红黑树中要对节点连接做两种颜色的区分，一说是因为当时的书写笔只有红色和黑色两种颜色，另一说是当时的打印机只有红和黑两种颜色。 　　1.1 红黑树的本质 　　什么是红黑树，红黑树的本质是什么？一句话就可以说清楚，红黑树是二叉树的身体、2-3 B树的灵魂，用计算机的语言来说就是，红黑树是二叉树的存储结构、2-3 B树的操作逻辑。那么红黑树为什么是这样的呢？这就和遗传学中的道理是一样的了，是为了取得杂交优势，既继承父本的优势又继承母本的优势，同时又抛弃了父本和母本的劣势。我们把二叉树看成是母本，2-3 B树看成是父本，母本的优势就是存储结构简单，还有比二叉树更简单的树形结构吗，没有了。父本的优势就是B树是绝对平衡树，任何时候都是绝对平衡的。但是父本的劣势也是因于此，为了实现绝对平衡，B树的存储结构比较复杂，当然操作逻辑也比较复杂。而二叉树虽然存储结构简单，操作也简单，但是它最大的缺点就是不一定平衡，一棵树如果不平衡，它的操作复杂度就会从O(logn)退化为O(n)，这是一个很严重的问题。为了实现一个既平衡又相对简单的树形结构，于是有人就想到了把二叉树和2-3 B树给结合起来，取二叉树的存储结构和2-3 B树的操作逻辑，用二叉树来模拟2-3 B树，于是红黑树就诞生了，这样红黑树就既实现了存储结构简单又实现了平衡的效果。红黑树的定义也就比较好理解了，就是为了保证红黑树在逻辑上是一颗2-3 B 树。我们这里暂时先不讲红黑树的定义，我们先来讲一讲2-3 B树，当你把B树的逻辑理解透了，那么掌握红黑树的定义和实现就易如反掌。这里说的二叉树具体来说是二叉搜索树，下文也会简单地讲一下。 　　1.2 B树简介 　　树形结构首先可以分为等叉树和不等叉树，等叉树是每个节点的键值个数都相同、子节点个数也都相同，不等叉树是每个节点的键值个数不一定相同、子节点个数也不一定相同。 　　最简单的等叉树是二叉树，直接二叉树的作用并不大，我们一般会要求二叉树所有的节点按照一定的顺序排列，这样我们进行插入、删除、查找时效率就会非常高，我们把这样的树叫做二叉搜索树或者二叉查找树。它的具体定义是这样的，二叉搜索树，要么是个空树，要么符合以下几个条件，1.左子树如果存在的话，左子树所有节点的键值都要小于根节点的键值，2.右子树如果存在的话，右子树所有节点的键值都要大于根节点的键值，3.它的所有子树也都要符合前面的两个条件(前面的小于同时换成大于也成立)。经过这样定义之后，二叉树就变成了二叉搜索树，它的插入、删除、查找效率一般情况下都是O(logn)。等叉树还有三叉树、四叉树、五叉树等，但是它们和二叉树相比，除了更复杂以外，好像也没有啥优点，所以很少听到有人用过。 　　不等叉树和等叉树相比除了更省空间以外，好像也没啥特别的用处，但是如果我们对不等叉树的节点键值数和插入、删除逻辑添加一些特殊的要求，使其能达到绝对平衡的效果，我们就把这种树叫做B树。B树全称Balance Tree，是一种自平衡树。它和等叉树最大的不同首先表现在存储结构上，等叉树上每个节点的键值数和分叉数都是相同的，而B树则不是。如果某个B树上所有节点的分叉数最大值是m，则把这个B数叫做m阶B树。下面我们来看一下B树的具体定义:所有节点最多有m个子节点。非根非叶子节点至少有m/2(向上取整)个子节点。根节点至少有两个子节点(除非总结点数都不够3个)。所有叶子节点都在同一层。任意节点如果有k个键值，则有k+1个子节点指针，键值要按照从小到大排列，子节点树上所有的键值都要在对应的两个键值之间。 　　B树的定义好像很复杂，但是仔细分析一下也不复杂，可以分为3类。一是对子节点的个数进行限制，包括1、2、3三条，1是限制最大子节点数的，这也是m阶B树的m的由来，2是限制非根非叶子节点的子节点数，叶子节点的子节点数是0，所以才叫叶子，没啥限制的，根比较特殊，下一条说，普通节点的子节点数至少要是m/2(向上取整)个，这么要求是为了提高树的紧凑性，避免树变得过于瘦高，3是限制根节点的子节点个数，要求根节点至少有2个子节点。二是要求整个树是要有序的，是5，第5条虽然不好用语言描述，但是它的意思是很简单明确的，就是键值要从小到大排序，键值之间的子节点的值也要在两个键值之间，如果是两端的，则要小于最小键值，或者大于最大键值。三是对树高的要求，是4，第4条说的是所有叶子都在同一层，也就是说每一个叶子的深度都是相同的，这也是整个树的高度，这一条直接规定了B树是一个绝对平衡树，不会出现退化成线性结构的可能，所以B树的效率一直是O(logn)的，没有例外情况。 　　B树的5条定义，其它的都好实现，就第4条比较难，而它也是B树保持绝对平衡的关键。那么第4条如何实现呢？这就要对它的插入和删除做特殊规定了。插入的时候只能在叶子节点进行插入，如果插入后叶子节点满了，则会对这个叶子节点进行分裂操作，选取中间键值把这个叶子一分为三，小于这个键值的重新组成一个节点，大于这个键值的重新组成一个节点，然后把这个中间键值送给父节点。如果父节点没有满，则插入操作结束。如果父节点也满了，则递归此操作，直至根节点。如果根节点也满了，则对根节点进行分裂，生成新的根节点，这时树的高度就会增加1，由于是在根部增长，所以所有节点的高度都增加了，整个树还是平衡的。总结起来，B树插入的特点就是底部插入、根部增长，而二叉树是底部插入、底部增长，时间长了容易生长不平衡，B树则没有这种烦恼，它一直都是平衡的。虽然B树的插入一直是平衡的，但是如果删除操作是直接执行的，也会导致B树被删的不平衡了，所以B树的删除也要特殊操作才行。B树的删除更加复杂，我们首先考虑如果被删除的键值不在叶子节点上，我们找到它的后继，它的后继一定是在叶子节点上，然后用后继覆盖它，再去删除这个后继，然后就是叶子节点的删除了。如果叶子节点里面的键值个数足够，删除一个也满足B树要求的个数，则直接删除，没有问题。如果自己的键值数不够了，则要考虑向临近的兄弟节点借，借的时候要经过父节点转手一次，并不是直接借人家的节点值，而是兄弟节点给父节点一个合适的键值，父节点再拿一个合适的键值给自己。如果兄弟节点也没有多余的键值可以借了，那就要向父节点借一个素并和兄弟节点进行合并处理，自己和左兄弟节点或者右兄弟节点再加上父节点的一个键值，合并成一个新的节点。如果父节点被借走了一个键值之后，键值数也小于要求了，则继续此过程，直至最后向根节点借，如果根节点也被借没了，则新合并的节点成为根节点，B树的高度减1。 　　我们对B树有了基本的了解，对B树的插入删除操作也有了大概的认识，但是可能还不是很清晰，下一章我们以2-3 B树为例，详细地讲一讲B树的操作逻辑。 　　视频讲解 　　通俗易懂的红黑树,B树,B+树 本质区别及应用场景（上） 　　通俗易懂的红黑树,B树,B+树 本质区别及应用场景（下） 　　LinuxC++后台服务器开发架构师免费学习地址 　　【文章福利】：小编整理了一些个人觉得比较好的学习书籍、视频资料共享在群文件里面，有需要的可以自行添加哦！~加入（需要自取）

　　二、2-3 B树的操作逻辑 　　2-3 B树是最简单的B树，它就是3阶B树，由于它的子节点个数是2或者3，所以大家都叫它2-3 B树。同理，4阶B树也被大家广泛的叫做2-3-4 B树，2-3-4 B树和2-3 B树差别并不大，因为一个4节点可以很轻松的转化为2个2节点，所以本文中就用2-3 B树的逻辑来实现红黑树，不再讨论2-3-4 B树的情况了。 　　2-3 B树就是3阶B树，我们把m阶B树的定义，把m=3代入进来看一下：所有节点最多有3个子节点。非根非叶子节点至少有3/2(向上取整)= 2个子节点。根节点至少有两个子节点(除非总结点数都不够3个)。所有叶子节点都在同一层。任意节点有k(1或者2)个键值，则有k+1个子节点指针，键值要按照从小到大排列，子节点树上所有的键值都要在对应的两个键值之间。 　　这个定义和B树的定义差别并不大，也没有多少简化，只不过是值具体化了而已。从这个定义中我们可以看出，2-3 B树中一共有两个类型的节点，2节点(单素节点)，3节点(双素节点)，后面为了叙述方便我们可能会混用这两对术语，后文也会混用素和键值这对词。我们先来看一个具体的2-3 B树，先有个大概的认识。

　　这是一个由0-9依次插入而形成的2-3 B树，图中的节点都是2节点和3节点，所有叶子节点都在最底层，高度是一样的，3的左子树都小于3，右子树都大于3，对于节点57来说，4小于5, 6大于5小于7, 8、9都大于7，符合B树的定义，B树的第5条定义虽然不好描述的，但是看图的话还是比较好理解的。但是B树的插入和删除操作是不太好理解的，下面我们用两节时间来详细讲一讲。 　　2.1 2-3 B树的插入操作 　　B树的插入并不是直接创建新节点，而是寻找在合适位置的叶子节点中插入素，把自己的键值加入到这个叶子节点中去，如果这个叶子节点原本就只有一个素，那么插入之后正好两个素，符合2-3 B树的要求，插入完成。如果这个叶子节点已经有两个素了，插入后就有三个素，那么就把中间的素送给父节点，自己分裂成两个节点。再看父节点，如果接收之后父节点也变成了3素节点，那么就重复这个过程，直到根节点。如果此时根节点也是3素节点，那么就把中间的键值拿出来创建新节点并成为新的根节点，原来的根节点分裂成两个节点挂在新的根节点上，整个2-3 B树的高度就增加了1。语言描述不太好懂的，下面我们用画图的方式详细讲一下把0-9依次插入一颗2-3 B树的过程。



















　　整个2-3 B树的插入过程还是很简单的，都是在寻找到自己对应位置的节点，如果那个节点本来只有一个素，再加入一个素也没有问题，过程就就结束了。如果那个节点本来有2个素就麻烦了，3个素挤在一起实在是太挤了，待不下，于是就把中间的素送给父节点，自己这个节点分成两个节点，左素和右素各占一个节点，新建立的两个节点连接到父节点上。如果父节点此时也变成了3个素，那就继续这一过程，直到根节点。如果到根节点还是3个素的话，把中间的键值单独建立节点，成为新的根节点，原来的根节点一分为二，分别连接到新的根节点上，这个新建立的中间节点成为新的根节点。 　　2.2 2-3 B树的删除操作 　　B树的删除逻辑是比较复杂的，首先要考虑的是删除的是不是叶子节点，如果不是叶子节点的话，先把它转化成叶子节点，转化的方式是找到它的后继素，然后把后继素的值复制给自己，然后把它的后继素给删了。这里面有两个问题，为什么这么操作是对的，怎么寻找后继素。这个留在本节的最后来回答。如果是叶子节点的话，那删除就相对简单了，如果这个叶子节点是双素节点的话，那就更简单了，直接把素删除了就行了，不会破坏2-3 B树的任何性质。如果叶子节点是单素节点的话，就比较复杂了，直接删除的话就违背了2-3 B树的性质了。为此我们需要先借一个素过来，要在不破坏2-3 B树的性质的情况下借，借到之后我们就变成了一个双素节点了，就可以直接删除素了。借的话也分几种情况，先给相邻的兄弟节点借，如果兄弟节点有两个素的话就可以借，借的方式不是直接拿过来，而是把被借的素给父节点，父节点再把另一个素借给自己，被借和借到的素不是同一个，这么做的目的是为了保持2-3 B树整体上仍然是有序树。如果从相邻的兄弟节点借不到，那就从父节点借，如果父节点有两个素的话就可以直接借，借来之后并不是直接加入到自己的节点中，而是自己和借来的素和一个相邻的兄弟节点合并成一个新节点，这么做是因为父节点少了一个素就少了一个子指针，所以得合并子节点才行。如果父节点是也是单素节点的话怎么办呢，没有办法，强行把父节点的一个素借过来，这时父节点空了，它就需要继续借，如果能从它的兄弟节点或者父节点借来就没事了，如果也借不来的话，就再强行向父节点的父节点借，一直持续这个过程，直到根节点。如果根节点也被借空了，那么整个2-3 B树的高度就会减少1。 　　我们同样以画图的方式把2-3 B树的删除过程给演示一遍。





















　　这几幅图详细地讲解了如何把前面建立的2-3 B树按照9-0的键值顺序依次删除。但是没有删除中间节点的情况，我们再举例说明一下删除中间节点的情况。



　　我们来解释一下前面留下来的疑问，为啥用后继素覆盖被删除素然后删除后继素是可行的。2-3 B树是一颗排序树，用后继素覆盖被删除素后，不考虑后继素节点，整个树还是一颗排序树，但是可能不是一颗2-3 B树了，所以对后继素节点走个删除流程，就能保证整个树还是2-3 B树。后继素如何寻找呢？首先我们可以发现2-3 B树是一个完整的树，也是说它的内部节点如果是一个单素节点它一定存在两个子节点，如果是一个双素节点，它一定存在3个子节点。对于任意内部节点的素，我们先到这个素紧邻的右子节点，然后在这颗子节点树上一直顺着最左子节点找到底，就能找到我们想要的后继素了。 　　三、红黑树的操作逻辑 　　当你明白了2-3 B树的操作逻辑之后，就基本明白了红黑树的操作逻辑，红黑树就是对2-3 B树的模拟，2-3 B树的一个节点可能有两个素，而二叉树的每个节点都只有一个素，那么如何模拟呢，二叉树给每个节点加了一个颜色属性，黑色就代表是正常的连接(图中的黑色都是用的蓝色)，红色就代表是内部连接，也就是原来的双素节点被分成了两个节点，它们之间用红色连接，代表二者本来是同一个节点的，下面我们就来看看这个模拟的过程。 　　我们首先来看单个节点是怎么怎么模拟的：

　　单个节点的转换是很简单的，单素节点还是单素节点，双素节点就有两种转换方式了，用哪种方式都可以，为了逻辑简单，我们都选择用左斜的转换方式。我们把前面生成的2-3 B树转换成红黑树试一下。

　　可以看到这个转换还是很简单的，转换前2-3 B树是一颗绝对平衡树，所有的叶子节点都在同一层，转换后虽然树变得不太平衡了，有的叶子节点高度变高了，但是可以看出叶子最高的高度与最低的高度顶多相差一倍，所以红黑树是一颗相对平衡树，相对平衡和绝对平衡都是平衡，都能保证树的操作复杂度是O(logn)。 　　3.1 红黑树的定义 　　我们把2-3 B树转换成红黑树之后能不能对这个红黑树任意操作呢？不能，因为任意操作之后可能就无法再转换回2-3 B树了，这就意味着这个红黑树可能不是平衡树了。因此我们要对红黑树进行定义，把对红黑树的操作限制在定义允许的范围内，这样红黑树就永远是红黑树，就一定对应着一颗2-3 B树，就一定是一颗平衡树。下面我们来看一下红黑树的定义。所有的节点不是黑色的就是红色的根节点是黑色的所有叶子节点是黑色的从每个叶子到根的所有路径上不能有两个连续的红色结点从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点 　　我们来分析这5条定义，1.所有节点都是黑色的或者红色的，这是肯定的了，要不然能叫红黑树嘛。2.根节点是黑色的，这是肯定的了，红色节点的含义是自己与父节点的连接是红色的，也就是说自己和父节点是内部节点，根节点没有父节点，只能是黑色的。3.所有的叶子节点都是黑色的，红黑树里规定把本来的每个叶子节点的左右子节点的那个空指针看做是NULL节点，看成是叶子节点，规定NULL节点是黑色的，这个规定好像没啥用，没有看出来这个规定的逻辑意义或者实现意义。4.从每个叶子到根的所有路径上不能有两个连续的红色结点，这一条是保证2-3 B树的每个节点都是2节点或者3节点。5.从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点，这一条是保证2-3 B树的所有叶子节点都是等高的。 　　有了红黑树的这五条定义就能保证红黑树永远是红黑树，永远都对应着一颗2-3 B树，永远都是一颗平衡树。这5条定义怎么记忆呢？我总结了4个四字短语来记忆，非红即黑、根黑叶黑、红子不红、黑径相等。 　　红黑树的定义只是给我提供了限制，我们的操作不能违背这个限制，但是红黑树的定义并没有告诉我们怎么操作红黑树，只要你的实现方法符合定义就行，下面我们来看一看红黑树应该如何操作。 　　3.2 红黑树的旋转与翻色 　　我们构建一颗红黑树并不是从2-3 B 树转换过来的，而是从一个空树，按照红黑树的构建规则不断地插入和删除而产生的一颗红黑树，在这个过程会出现很多的3素节点需要我们来处理。一个3素节点会对应怎样的红黑树片段呢，我们会遇到怎样的情况呢，遇到了又应该怎么处理呢，下面我们来看一下。 　　3素节点的处理是红黑树的重点，也是难点，掌握了这个也就基本掌握了红黑树。

　　3素节点转换为二叉树节点会有这五种可能的情况，当然我们不会把3素节点转换成奇奇怪怪的形态，我们一般会把3素节点转换成标准形态，这样比较好处理。但是我们在处理红黑树的过程中也会遇到这四种非标准形态，如果遇到的话，就用下面的方法把它们转为标准形态再进行翻色就可以了。

　　标准形态本身并没有违背红黑树的定义，所以红黑树中可以存在标准形态。但是本文用的是2-3 B树模型，遇到了标准形态都会进行翻色处理，所以最终的红黑树上不会有标准形态的，只有中间的处理过程中会产生标准形态。翻转颜色(color flip)这个操作，不违背红黑树的前三条定义，也不违背黑径相等的定义，但是有可能违背红子不红的定义。这是因为所有过7 8 的路径以前有一个黑径，现在还是一个，对于过8 9的路径也是如此，翻转前后过7 8和8 9的路径和黑色节点数不会发生变化。翻色分为向上翻色和向下翻色，向上翻色用于插入操作中，有可能会违背红子不红的规定，因为8的父节点有可能还是红色的，所以对这个问题要一直往上回溯处理。向下翻色用于删除操作中，不会违背红子不红的定义。



　　可以看到非标准形态可以通过一次左旋和一次右旋转换成标准形态。那么自旋又是怎么操作的呢？



　　从B树的角度来看左旋和右旋，左旋右旋改变的是一个节点内部的连接，并没有改变B树本身任何的性质。从二叉树的角度来看，左旋右旋不会改变红子不红的问题，原来有红子不红的现在还继续有，原来没有现在还没有。通过数过A B C的路径的黑径数可以发现其前后不变，所以左旋右旋没有违背红黑树黑径相等的定义。当我们把旋转和翻色都学明白之后就可以开始研究红黑树是怎么模拟2-3 B树的插入操作了。 　　3.3 红黑树的插入操作 　　本文实现的是左斜红黑树，也就是所有的红色节点都是左子节点。红黑树插入的时候节点默认颜色是红色，这个和2-3 B树的所有键值只插入叶子节点是一致的，而且增加一个末端的红色节点不会违背红黑树黑径相等的定义，但是有可能违背红色不红的定义，所以要通过旋转和翻色来解决这个问题，并要递归解决这个问题，直至根节点。节点插入之后首先要先考虑自己是否构成3素节点，如果不构成的话就结束了，如果构成的话，就要进行处理，构成的条件是父节点是红色或者父节点的另一个子节点是红色，如果两个子节点都是红色就要进行翻色处理，如果子节点和父节点是红色节点，则要按照前面说的非标准形态进行处理，先转换成标准形态，再进行翻色。处理完成之后继续对父节点进行同样的处理，直至根节点。 　　下面我们来看一看红黑树模拟2-3 B树的插入操作的过程，加深对红黑树插入操作地理解。











　　可以看出红黑树一直都在进行寻找3素节点，也就是两个连续的红色或者相邻的红色，然后进行旋转和翻色操作，直至整个红黑树都符合红子不红的定义为止。 　　3.4 红黑树的删除操作 　　红黑树的删除操作比较复杂，分为很多种情况，我们先来看几个示例







　　红黑树的删除有很多种情况，最简单的就是要删除的节点是叶子节点并且是红色，直接删除就行了，然后是自己没有右子，自己的左子是红色，和左子做一个右旋就变成了前面的情况，可以直接把自己删除。如果这两种情况都不是，那就想办法把自己变成红色节点了，对应2-3 B树中的操作就是借素。红黑树的删除过程还有一些更复杂的过程，我们在下一章实现里面再细说。 　　四、红黑树的实现 　　理解了上面大部分的逻辑之后，我们就可以开始去实现红黑树了，本文用C语言实现了2-3 B树对应的左斜红黑树。 　　4.1 结构体定义 　　首先我们要定义红黑树的结构体和接口。rbtree.h 　　这个文件也很简单，定义了红黑树节点rbnode，颜色枚举值RED BLACK，以及rbtree，rbtree用来放置红黑树的根节点和一些其它信息。还声明了红黑树的三个接口函数insert、delete 和 find。 　　对于红黑树来说，find的实现很简单，二叉搜索树的查找： 　　rbtree.c 　　红黑树本身也是个二叉搜索树，所以它的查找函数和二叉搜索树的查找是一样的。 　　4.2 翻色与旋转代码 　　下面我们来说下翻色与旋转函数的实现rbtree.c 　　翻色函数很好理解，向上翻色就是把自己变红，把左子和右子都变红，向下翻色正好相反。 　　再来看一下旋转函数rbtree.c 　　我们以左旋为例讲解一下。左旋旋转的是自己和右子，往左旋把自己旋下去了，把右子旋上来了，右子占据了自己的位置，自己成了右子的左子。函数首先做的是交接parent，把右子先挂到parent上去，然后把右子的左子挂接到自己身上，接着让自己成为右子的左子，最后交换二者的颜色，这么做是为了保持两者的连接颜色不变。右旋的逻辑是类似的，这里就不再多讲解了。 　　4.3 插入操作的代码 　　代码如下，主要是两个函数，insert和insert_fix。rbtree.c 　　函数insert的逻辑很简单，就是创建新的节点，新节点的颜色设为红色，按照二叉搜索树的方式寻找要插入的位置，然后调用insert_fix,来保证整个树是一个符合定义的红黑树。insert_fix的实现主体是一个while循环，当x的parent存在时就一直循环，直到x是根节点为止，当然while内部有提前结束循环的地方。进入循环体内，首先我们要明白的就是，此时x的颜色是RED，这是因为第一次循环的时候x是RED的，后面循环再次进来的时候x也是RED的，如果不是的话就不会继续循环了。先分x是左子还是右子两种情况来讨论，当x是左子的时候，看parent是不是RED，如果是BLACK的话，直接return。如果是RED的话，此时x和y都是左斜的，y是左斜的是因为我们实现的是左斜红黑树，原有的红色节点只可能是左斜的。对于双红色左斜节点的处理，我把图片又放到下面了，大家可以再看一看。这种情况我们应当对y的parent进行右旋，右旋之后，y成了两个红色节点的父节点，由于旋转之前y是红色，所以y的parent不可能是红色，只能是黑色，所以旋转之后交换了颜色，所以此时y肯定是黑色。y是黑色，左子右子都是红色，正好可以翻色，翻色之后，左子右子都变成了黑色，y变成了红色，让x=y进行下一轮循环。当x是右子的时候，先看一下左兄弟是不是红色，如果是的话，父节点y肯定是黑色，正好可以翻色，对y进行翻色，让x=y，继续下一轮循环。如果x的左兄弟不是红色的，先左旋y，左旋之后x y的父子关系变了，交换一下它们的值，让x仍然是子，y仍然是父。判断y的颜色，如果是黑色直接return函数结束，如果是红色，x y又形成了双左斜红色的情况，和上面的处理方式是一样的，右旋y的parent，翻色y，让x=y，继续下一轮循环。函数最后判断根节点是否为红色，如果为红色的话，说明之前的根节点经历过分割，树的高度增加1，再把根节点重置为黑色。

　　4.4 删除操作的代码 　　删除操作主要有两个函数，delete 和 delete_fix，delete比insert稍微复杂一点，要处理被删除的点不是叶子节点的情况。对于非叶子节点的情况，其右子树一定存在，用右子树的最小值，也就是右子树的最左子节点的值覆盖自己，然后删除右子树的最左子节点就可以了。 　　rbtree.c 　　函数delete_fix首先考虑两种特殊情况，如果node是红色的，或者node的左子是红色的，直接右旋自己，把自己变成红色，然后直接goto delete。剩下的情况就是node不是红色的，也是说node是单素节点，要想办法把自己变成红色的，也就是通过借素变成双素节点。进入循环的条件是当前素的parent不为空，循环内部有一个变量red_borrowed控制着是否继续循环，如果为1则循环，如果为0则结束循环，也就是说循环至少会执行一次，然后x->parent和red_borrowed共同决定是否继续循环。循环体内分为两种情况，自己是左子和自己是右子的情况，自己是左子的情况又分两种，自己是右子的情况又分四种。下面通过画图给大家解析一下。字母与代码中对应的节点如下： 　　x:self 　　y:parent 　　z:brother 　　w:nephew(侄子)

　　注意在每次循环开始的时候x都是黑色的。由于我们是左斜红黑树，所以z不可能是红色的，可能的情况只有w是红色的或者是黑色的(下一种情况)，对于这种情况，我们通过其对应的2-3 B树可以看出来我们应该如何把红黑树调整成目标的样子。我们先把w的颜色置黑，因为它最终的颜色是黑色的，提前置黑能避免旋转时的颜色交换。然后通过右旋z、左旋y把红黑树调整成目标形态，然后把x的颜色置红，然后再根据red_borrowed把x置黑。此种情况我们帮x借到了红色，对应着2-3 B树中借到了素，所以循环结束。

　　这种情况是兄弟节点没法借的情况，只有向父节点借，向父节点借有两种情况，一是父节点是红色，能借到，循环就结束了，二是父节点是黑色，借不到，只能强行借了，把red_borrowed设置为1。我们还要考虑上一轮的red_borrowed，如果为1，要把借来的红色还了，也就是说x刚借来红色就还了，x还是黑色的。如果red_borrowed为0的话说明是第一次循环，x是要被删除的素，所以不存在违背红子不红的问题。如果这一轮的red_borrowed是1的话则继续循环，否则就结束循环。

　　这是一种比较复杂的情况，对应着2-3 B树的情况是父节点和兄弟节点都有两个素的情况。看红黑树比较复杂，我们看2-3 B树是怎么操作的，通过B树的操作反推红黑树应该如何操作。第一步我们右旋y，得到了一个x y o n ，一个局部有红色节点的树。第二步，只考虑这个树，我们最后可以通过右旋y并调整颜色的方式把红色转移给x，这样我们就达到目的了。然后我们发现o的颜色是右斜的，对z左旋一下，把它调整为一个左斜红黑树。

　　这种情况对应的2-3 B树是父节点有两个素，向父节点借一个素并和兄弟节点合并，所以我们先右旋y，然后对y进行翻色，x就变为红色了。通过前面的分析我们知道，虽然x是红色右斜的，但是有两种情况，要么x是被借红的，所以还会变成黑色，要么x就是要被删除的节点，所以不需要把x旋转为左斜的。

　　这种情况是父节点只有一个素兄弟节点有两个素，直接向兄弟借素，一个右旋y并调整颜色，就搞定了。

　　这种情况和左2是相同的，而且还比左2简单，由于z是左斜的，所以旋转的动作都省了。 　　五、总结回顾 　　红黑树是二叉树和2-3 B树结合而成的一种数据结构，理解红黑树的关键在于理解B树的操作逻辑，理解了B树就基本理解红黑树，红黑树的难点在于3素节点的旋转和翻色操作。本文先论述了红黑树和2-3 B树之间的关系，然后用画图的方式详细讲解了2-3 B树的操作逻辑，接着又用画图的方式了讲解了红黑树是如何模拟2-3 B树的操作逻辑的，最后用C语言实现了一个左斜红黑树。 　　参考文献： 　　《Introduction to Algorithms》 　　《Data Structures and Algorithms in Java, 6th Edition》 　　《Left-Leaning Red-Black Trees》 　　本文的源代码放到github上去了，大家可以参考一下 　　https://github.com/orangeboyye/rbtree 　　原文：深入理解红黑树_城中之城的博客-CSDN博客