电路-品质因数_谐振电路的品质因数Q怎么求

2024年 7月 4日下午9:47 • 激活谷笔记

物理意义
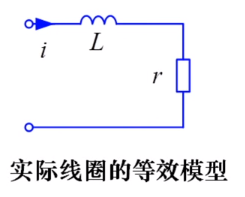
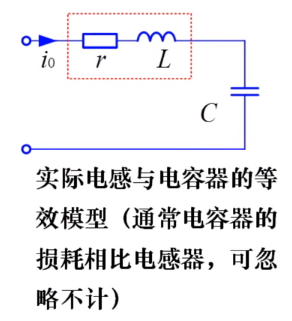
- 电感线圈、电容器品质因数：用于评价实际电感线圈、电容器的品质。实际电感、电容除储存能量外，都存在一定能量消耗。
- 件品质因数定义： $\overset{\underset{\mathrm{def}}{}}{=} 2\pi\frac{储能的最大值}{一周期内的耗能}$
- 品质因数用来衡量件质量的好坏，将品质因数扩展到谐振电路，表示谐振电路储能与耗能的比值。

线圈电流： $\sqrt{2}Icos\omega t$
电感储能： $w_{L}(t)=\frac{1}{2}Li^{2}=LI^{2}cos^{2}\omega t$
最大储能为： $LI^{2}$
一周期内线圈内阻r的耗能： $I^{2}rT$
电感品质因数： $Q_{L}=2\pi\frac{LI^{2}}{I^{2}rT}=\frac{2\pi fL}{r} =\frac{\omega L}{r}$

电容电压： $u=\sqrt{2}Ucos\omega t$
电容储能： $w_{C}(t)=\frac{1}{2}Cu^{2}=CU^{2}cos^{2}\omega t$
最大储能： $CU^{2}$
一周期电阻R耗能： $\frac{U^{2}}{R}T$
电容品质因数： $Q_{C}=2\pi\frac{CU^{2}}{U^{2}GT}=\frac{2\pi fC}{G} =\frac{\omega C}{G}=\omega CR$

电路谐振时，回路电流： $i=\sqrt{2}cos\omega _{0}t$
电容电压相量： $\dot{U_{C0}}=-j\frac{1}{\omega _{0}C}\dot{I_{0}}=\frac{I_{0}}{\omega _{0}C}\angle 90^{o}$
电容电压瞬间式： $u_{c0}=\sqrt{2}\frac{I_{0}}{\omega _{0}C}cos(\omega _{0}t-90^{o})=\sqrt{2}\frac{I_{0}}{\omega _{0}C}sin(\omega _{0}t)$
电感储能： $w_{L0}(t)=\frac{1}{2}Li_{L0}^{2}=LI_{0}^{2}cos^{2}\omega_{0}t$
电容储能： $w_{C0}(t)=\frac{1}{2}Cu_{C0}^{2}=C(\frac{I_{0}}{w_{0}C})^{2}sin^{2}\omega_{0} t$
条件：谐振电路中 $\omega_{0}L=\frac{1}{\omega_{0}C}$
可得电容储能等于电感储能： $w_{C0}(t)=C(\frac{I_{0}}{w_{0}C})^{2}sin^{2}\omega_{0} t=LI^{2}sin^{2}\omega_{0} t$
谐振电路的总储能为电感储能与电容储能之和： $w_{0}(t)=w_{L0}(t) +w_{C0}(t)=LI^{2}_{0}=CU^{2}_{0},(常数)$
当电感储能最大时电容储能为零，反之亦然。
谐振电路谐振时的品质因数： $Q=2\pi\frac{LI^{2}_{0}}{I^{2}_{0}rT_{0}}=\frac{w_{0}L}{r}=\frac{1}{w_{0}Cr}$
谐振电路品质因数反映电路选频特性，品质因数越高，选频特性越好。