1. 激活谷首页
  2. 激活谷笔记

白点黑点匹配贪心算法_什么是假点匹配

• 激活谷笔记

白点黑点匹配贪心算法_什么是假点匹配

(二)黑白点的匹配（Problem Set 1714）：

1.问题描述

设平面上分布着n个白点和n个黑点，每个点用一对坐标（x, y）表示。一个黑点b=（xb,yb）支配一个白点w=(xw, yw)当且仅当xb>=xw和yb>=yw。若黑点b支配白点w，则黑点b和白点w可匹配（可形成一个匹配对）。在一个黑点最多只能与一个白点匹配，一个白点最多只能与一个黑点匹配的前提下，求n个白点和n个黑点的最大匹配对数。

2.具体要求

Input
输入的第一行是一个正整数k，表示测试例个数。接下来几行是k个测试例的数据，每个测试例的数据由三行组成，其中第一行含1个正整数n(n<16)；第二行含2n个实数xb1, yb1,xb2, yb2,…, xbn, ybn， (xbi, ybi)，i=1, 2, …, n表示n个黑点的坐标；第三行含2n个实数xw1, yw1,xw2, yw2,…, xwn, ywn，(xwi, ywi)，i=1, 2, …, n表示n个白点的坐标。同一行的实数之间用一个空格隔开。

Output
对于每个测试例输出一行，含一个整数，表示n个白点和n个黑点的最大匹配对数。

3.测试数据 Sample Input 1 3 5.0 3.0 5.0 -1.0 4.0 4.0 2.0 3.5 2.0 2.0 -2.0 -2.0 Sample Output 3

我的贪心思路：

1

.先将黑棋和白棋可匹配和不可匹配关系用一个二维数组保存
可匹配为1，不可匹配为0
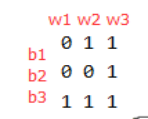
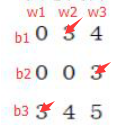
计算出如下图b1,b2,b3是黑点 w1,w2,w3是白点 1代表可以匹配，0代表不能。
在这里插入图片描述

计算代码如下
在这里插入图片描述

2

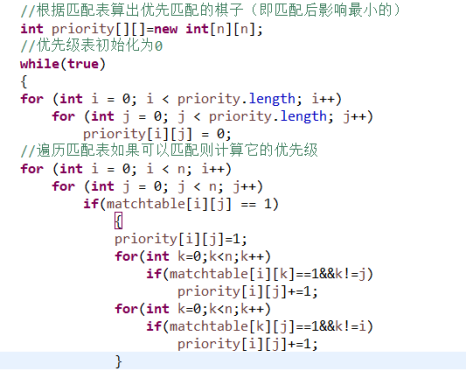
.根据上面的匹配表算出优先匹配的棋子
如果是可匹配那么计算出它的匹配后会影响到多少个棋子在这里插入图片描述

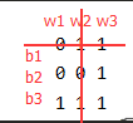
如图b1和w2它们可匹配，如果它们匹配会影响到w3的一个选择和b3的一个选择 横行和竖行有3个1
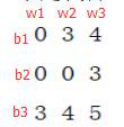
于是我得到一个这样的表
在这里插入图片描述

计算的代码如下：
在这里插入图片描述

3

.影响最小则匹配优先级最高（贪心选择）
因为如果先匹配了影响大的可能会造成：
影响小的匹配点被PASS掉了（一个白点只能和一个黑点匹配）
这样匹配数量就变少了
在这里插入图片描述在这里插入图片描述

如图影响最小是3 有3个匹配从中随便选一个 //按顺序就选b1,w2

4

.选择影响最小的匹配完后更新匹配表
在这里插入图片描述
变成在这里插入图片描述

5

.判断是否匹配完了，没有就重复2。

附上代码：

import java.util.Scanner; public class ChessMatch { 
    static int[][] Calculated_Matchtable(float[] xb,float[] yb,float[] xw,float[] yw) { 
    int[][] matchtable = new int[xb.length][xb.length]; // 先默认都不能匹配 for (int i = 0; i < matchtable.length; i++) for (int j = 0; j < matchtable.length; j++) matchtable[i][j] = 0; // 可以匹配的点设置为1 for(int i=0;i<xb.length;i++) for(int j=0;j<xb.length;j++) if(xb[i]>=xw[j]&&yb[i]>=yw[j]) matchtable[i][j] = 1; return matchtable; } static void solution1(int[][] matchtable) { 
    int n=matchtable.length; int count=0; //根据匹配表算出优先匹配的棋子（即匹配后影响最小的） int priority[][]=new int[n][n]; //优先级表初始化为0 while(true) { 
    for (int i = 0; i < priority.length; i++) for (int j = 0; j < priority.length; j++) priority[i][j] = 0; //遍历匹配表如果可以匹配则计算它的优先级 for (int i = 0; i < n; i++) for (int j = 0; j < n; j++) if(matchtable[i][j] == 1) { 
    priority[i][j]=1; for(int k=0;k<n;k++) if(matchtable[i][k]==1&&k!=j) priority[i][j]+=1; for(int k=0;k<n;k++) if(matchtable[k][j]==1&&k!=i) priority[i][j]+=1; } //显示优先级表 System.out.println("优先级:"); for (int i = 0; i < priority.length; i++) { 
    for (int j = 0; j < priority.length; j++) System.out.print(priority[i][j]+" "); System.out.println(); } //找到优先级最大的 int min=n*n; int indexi=0; int indexj=0; for (int i = 0; i < priority.length; i++) for (int j = 0; j < priority.length; j++) if(min>priority[i][j]&&priority[i][j]!=0) { 
    min=priority[i][j]; indexi=i; indexj=j; } //优先级最大的先匹配，更新匹配表 for (int i = 0; i < n; i++) matchtable[i][indexj] = 0; for (int j = 0; j < n; j++) matchtable[indexi][j] = 0; //显示更新后的匹配表 System.out.println("更新后的匹配表:"); for (int i = 0; i < matchtable.length; i++) { 
    for (int j = 0; j < matchtable.length; j++) System.out.print(matchtable[i][j]+" "); System.out.println(); } count++; //判断是否匹配完了 int matchnum=0; for (int i = 0; i < n; i++) for (int j = 0; j < n; j++) if(matchtable[i][j] == 1) matchnum++; if(matchnum==0) break; } System.out.println("结果："+count); } public static void main(String[] args) { 
    Scanner scan = new Scanner(System.in); int t = scan.nextInt(); System.out.println("测试次数：" + t); int n ; int k ; while (t != 0) { 
    n = scan.nextInt(); k=n; System.out.println("输入顶点个数：" + n); float xb[] = new float[n]; float yb[] = new float[n]; float xw[] = new float[n]; float yw[] = new float[n]; int matchtable[][] = new int[n][n]; while (n != 0) { 
    xb[xb.length - n] = scan.nextFloat(); yb[yb.length - n] = scan.nextFloat(); n--; } while (k != 0) { 
    xw[xw.length - k] = scan.nextFloat(); yw[yw.length - k] = scan.nextFloat(); k--; } // 计算每个节点，可匹配为1，不可匹配为0 matchtable = Calculated_Matchtable(xb, yb, xw, yw); System.out.println("匹配表"); for (int i = 0; i < matchtable.length; i++) { 
    for (int j = 0; j < matchtable.length; j++) System.out.print(matchtable[i][j]+" "); System.out.println(); } solution1(matchtable); t--; } } }

结果：

在这里插入图片描述

结果分析和思考

从网上看了很多题解，但是感觉答案都好像不是很对。于是自己想到了一个思路。
根据结果来看是得出了比较正确的结果，但是我不会证明这个解是全局最优解，但是值得一提的是我还没有找到一个返例来推翻它。为了让思路更清晰代码写了很长。

2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/161989.html

赞 (0)
0
上一篇 2024年 7月 5日 下午6:14
下一篇 2024年 7月 5日 下午6:18

相关推荐

关注微信