目录
一. 差异性分析简介
1)差异性分析
2)假设检验
3)差异性分析类型
二. 单个总体差异性的假设检验
1)单个总体均值
(a)σ已知的情况:z检验(例5.1)
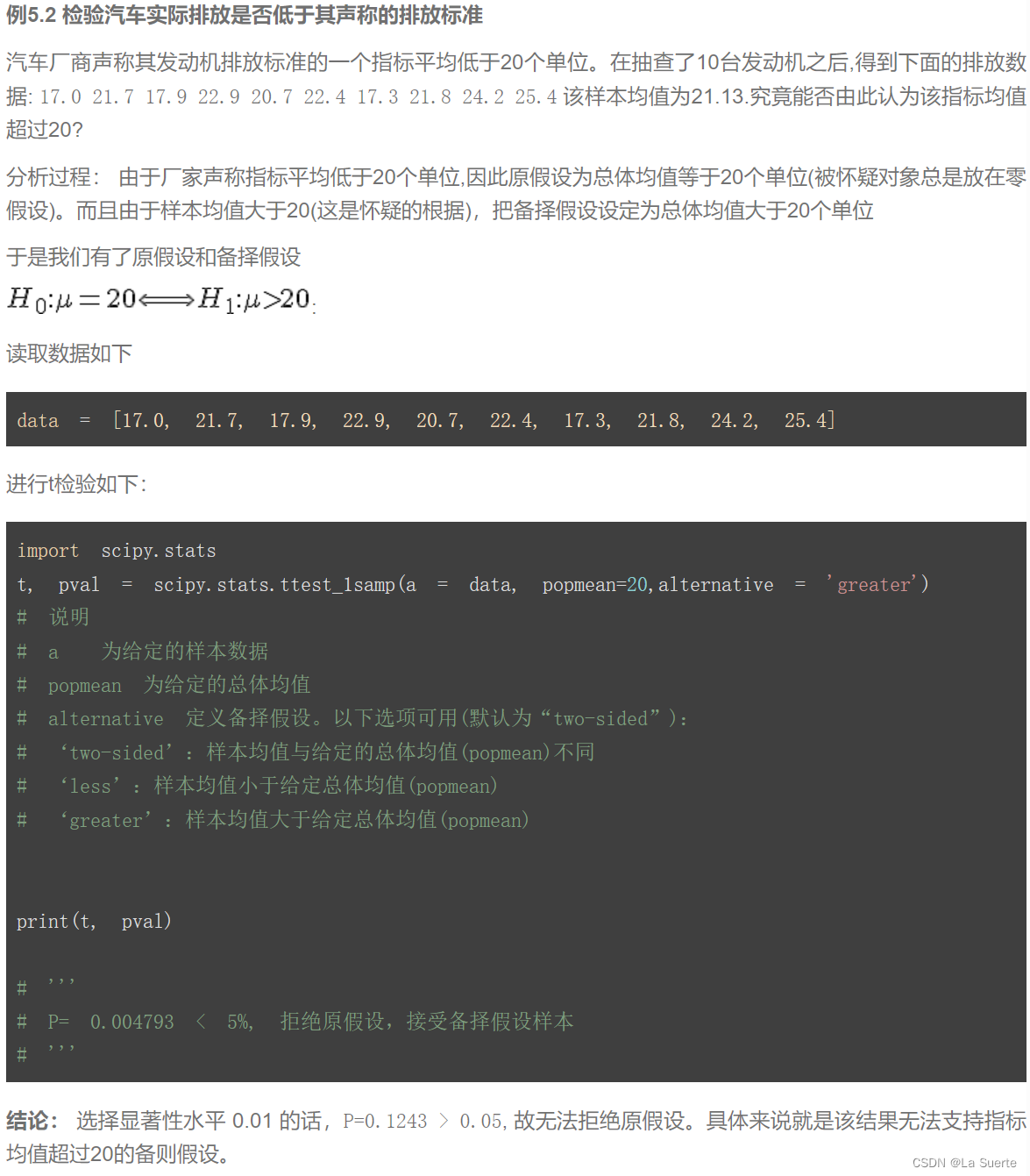
(b)σ未知的情况:t检验(例5.2)
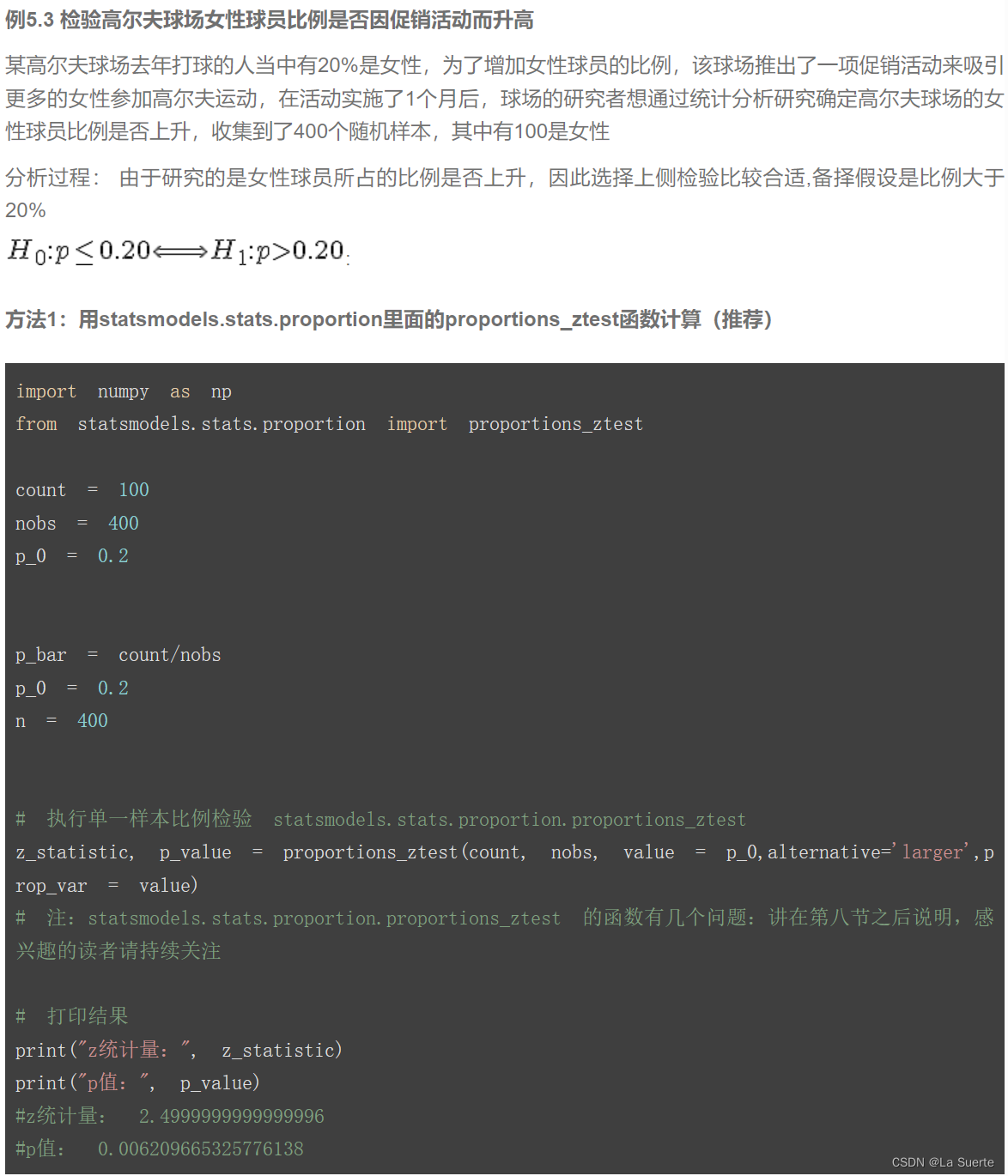
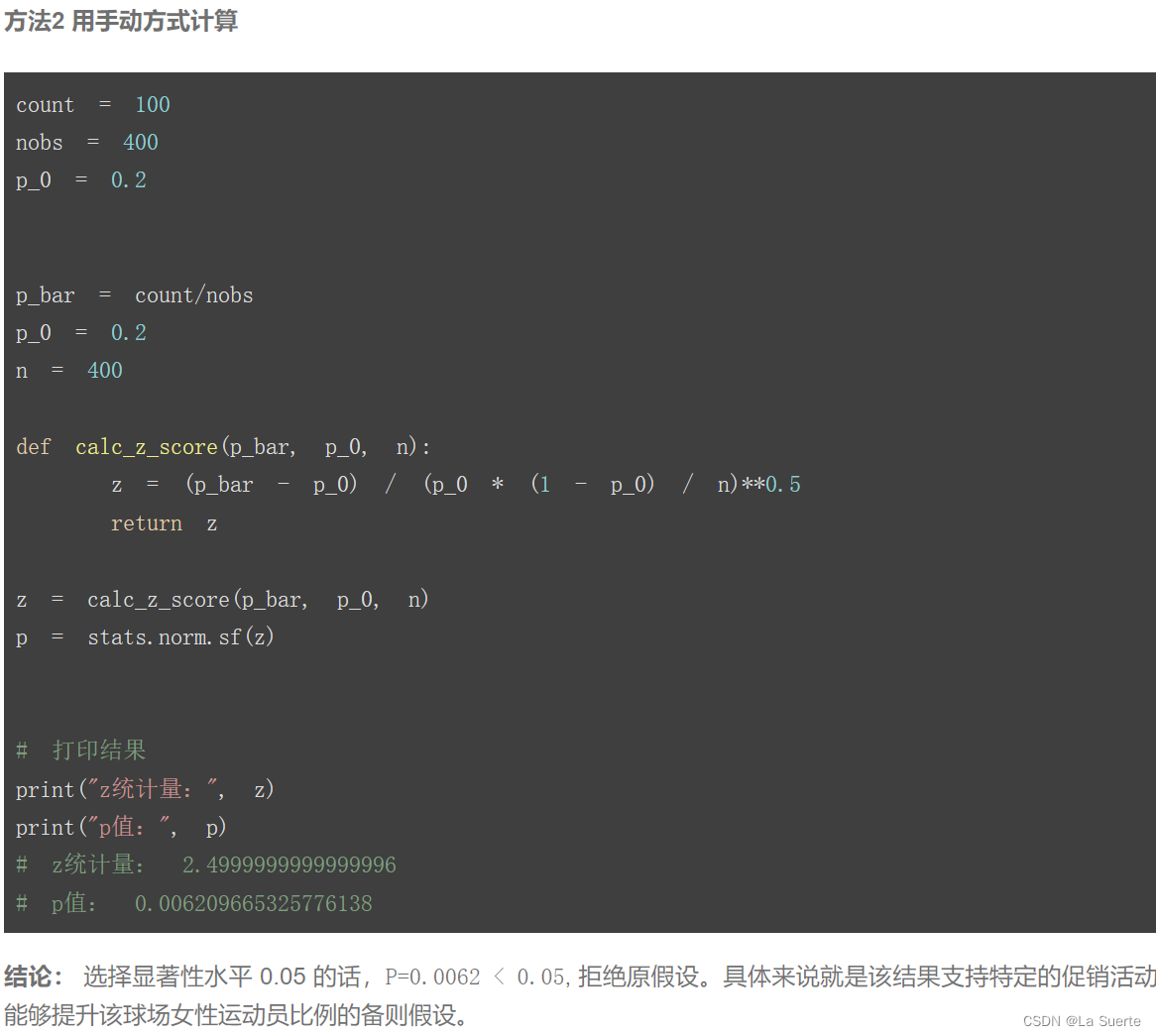
2)单个总体比例(例5.3)
3)单个总体方差
(a)例5.4
(b)例5.5
三. 两个总体差异性的假设检验
1)两总体均值之差
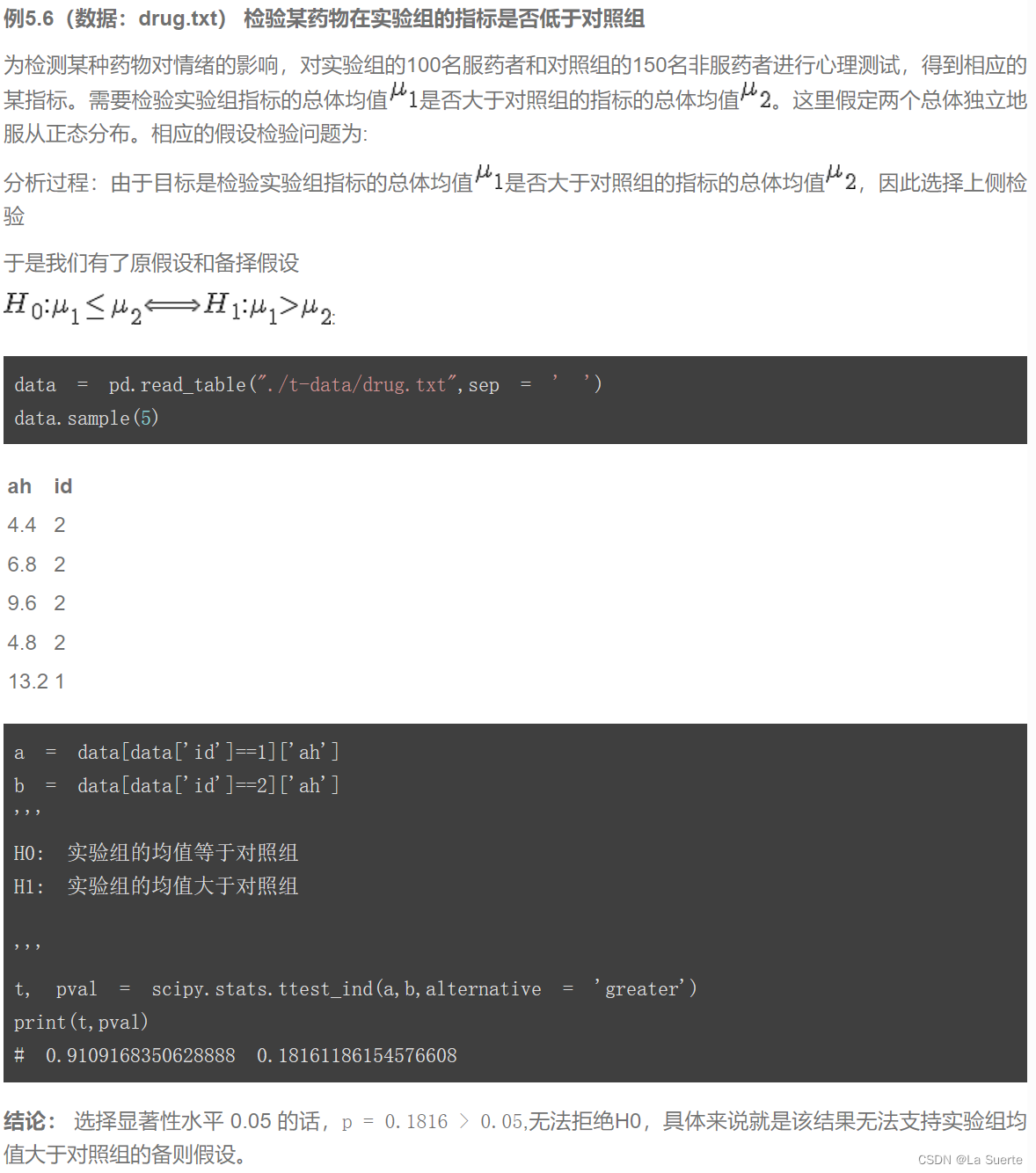
(a)独立样本(例5.6)
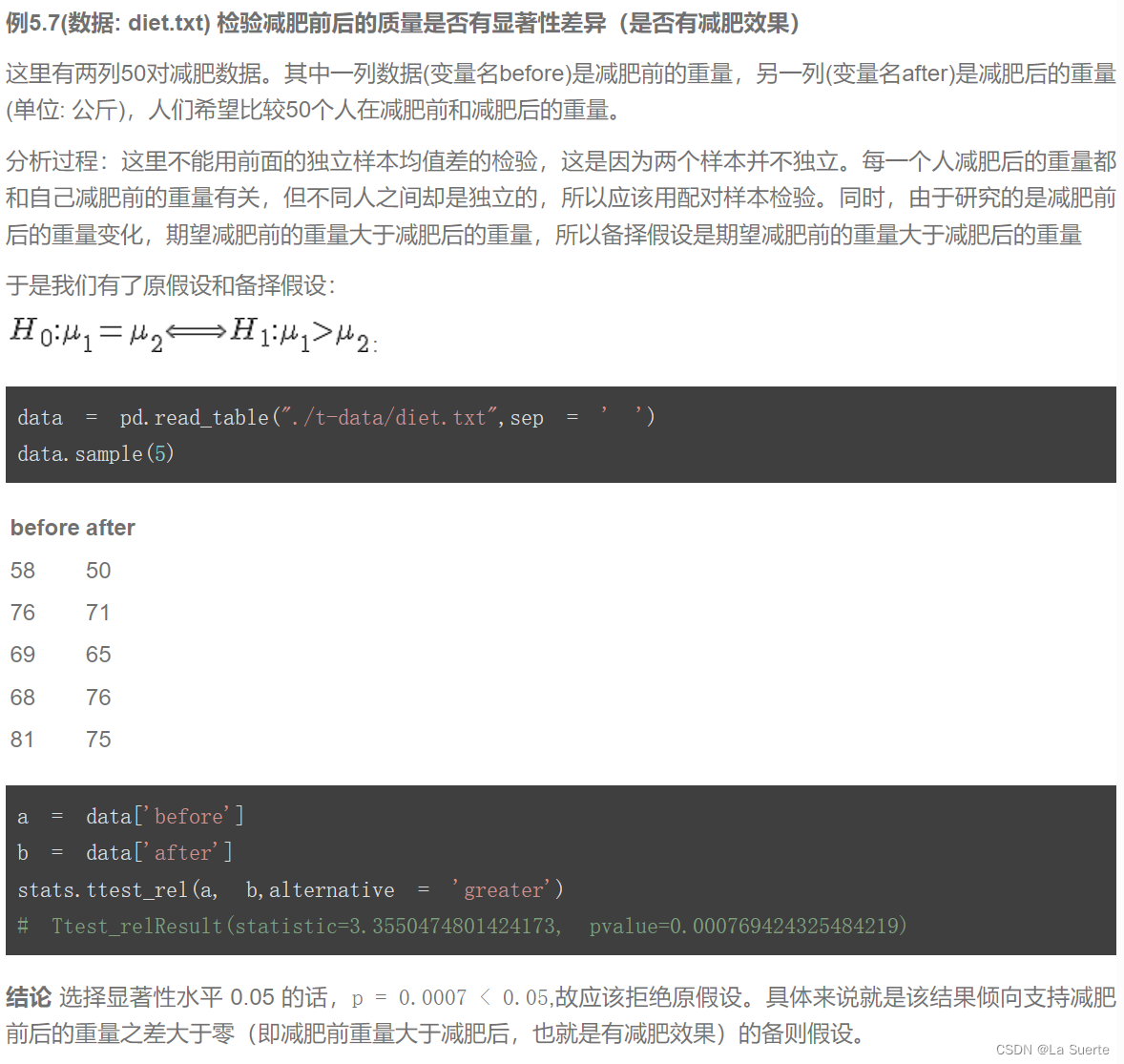
(b)配对样本(例5.7)
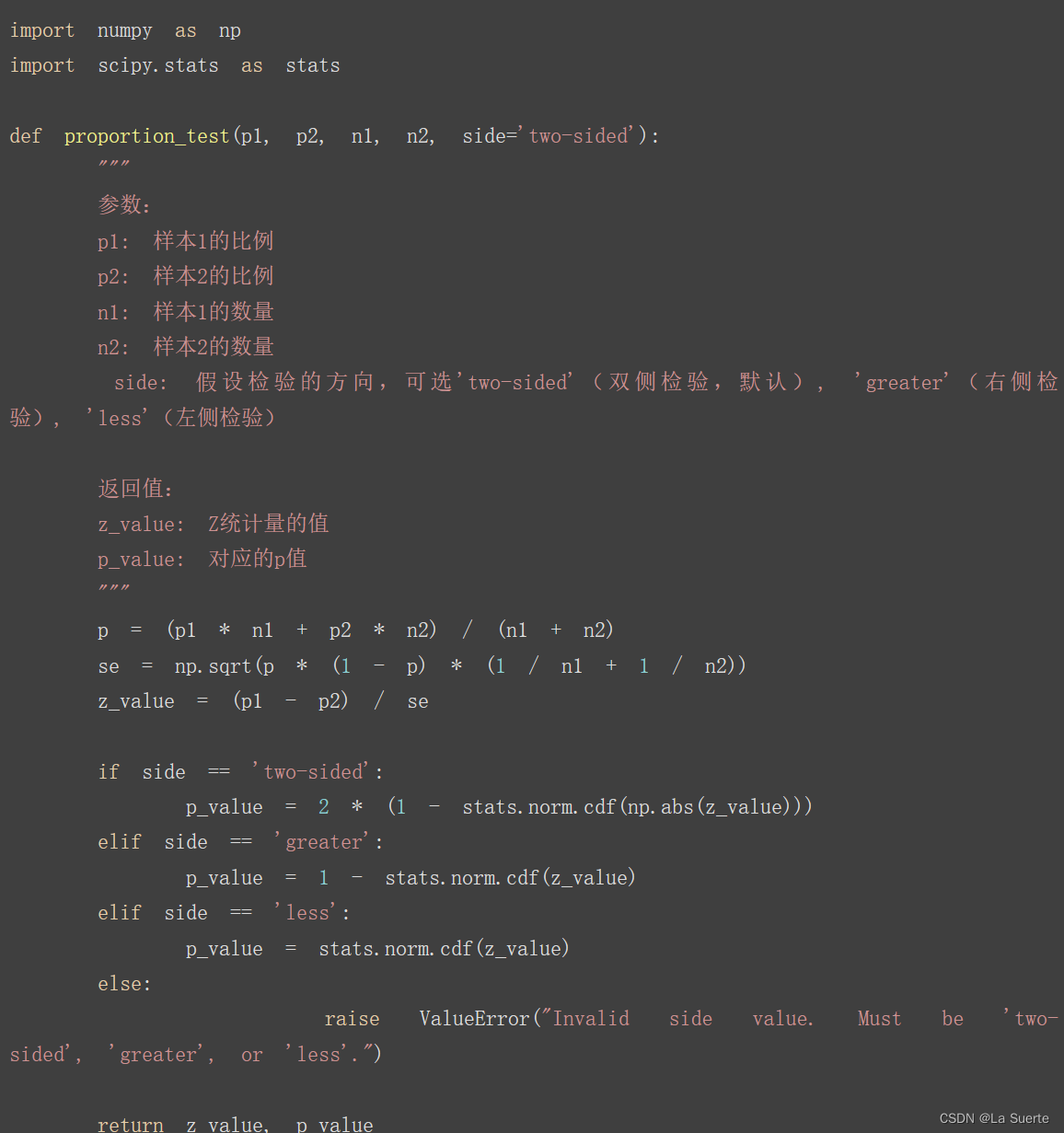
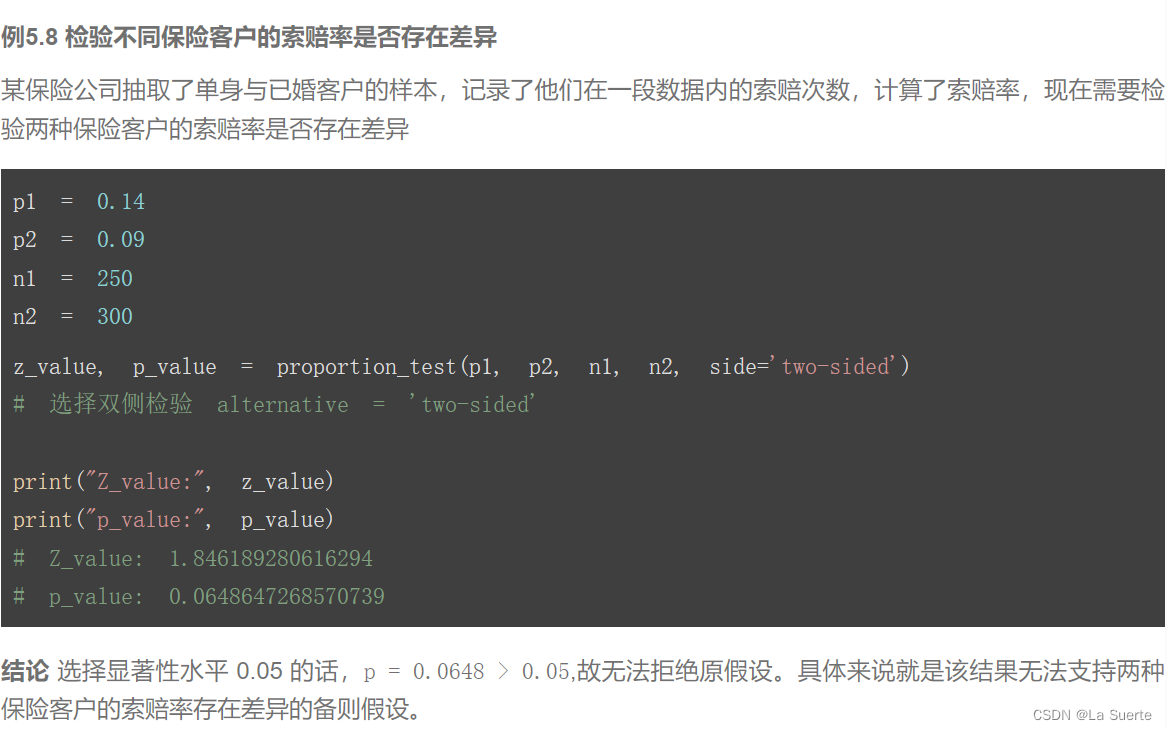
2)两总体比例之差(例5.8)
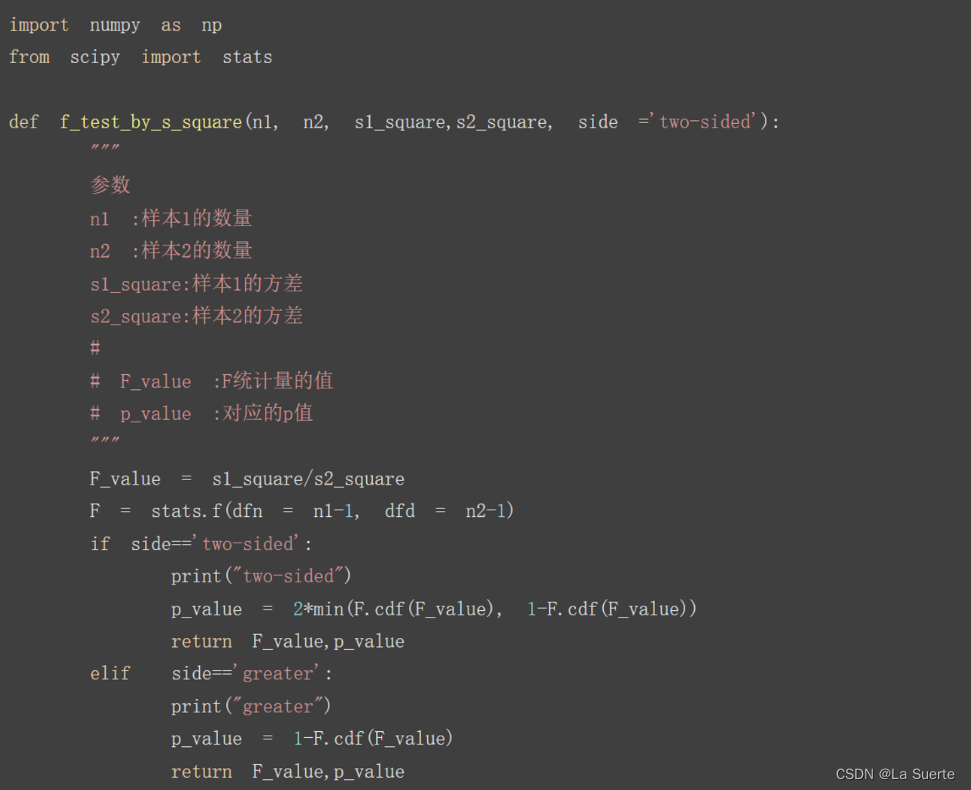
3)两总体方差之比
(b)例5.9
(c)例5.10
四. 方差分析
1)单因素多水平方差分析
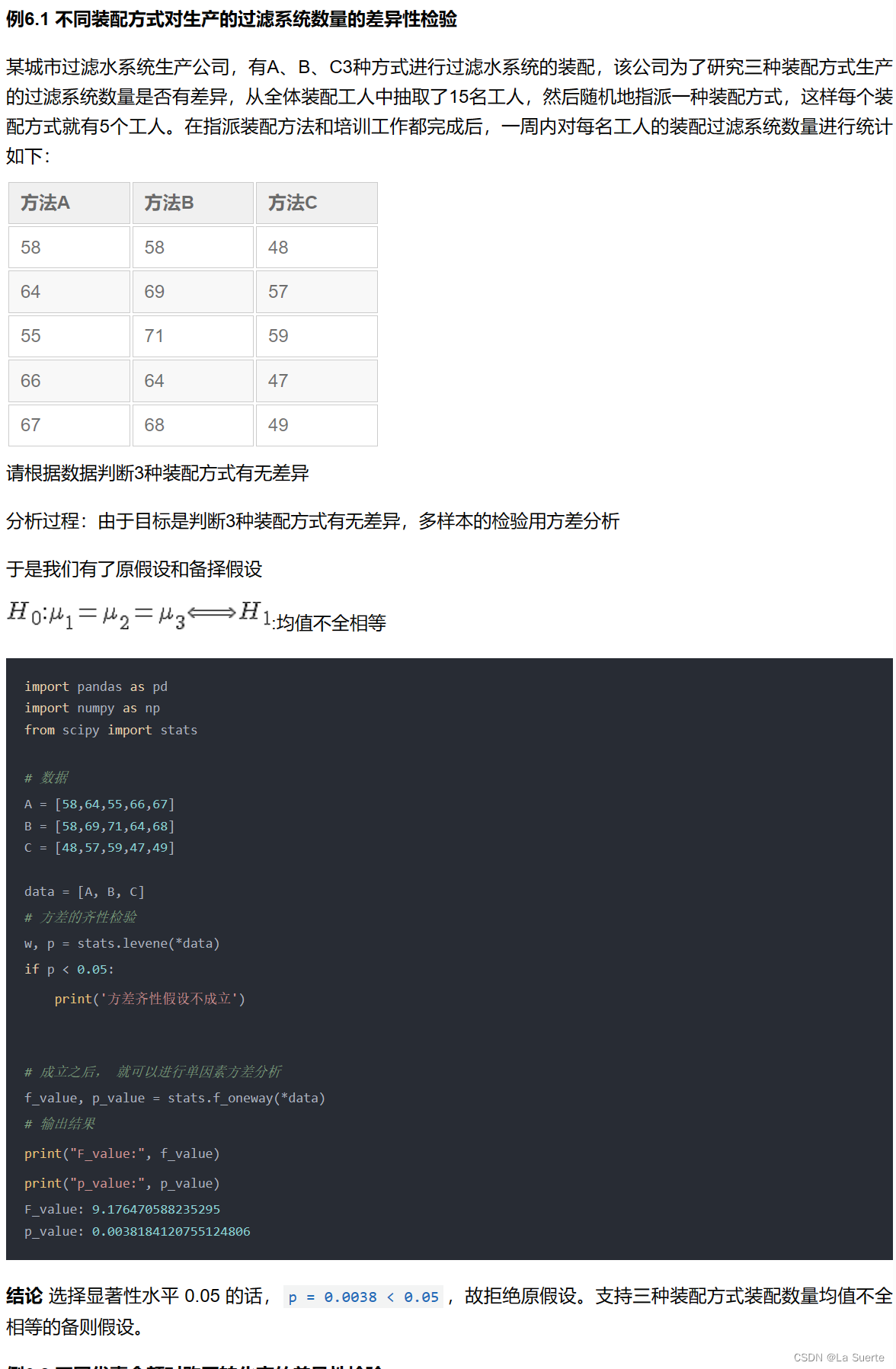
(a)例6.1
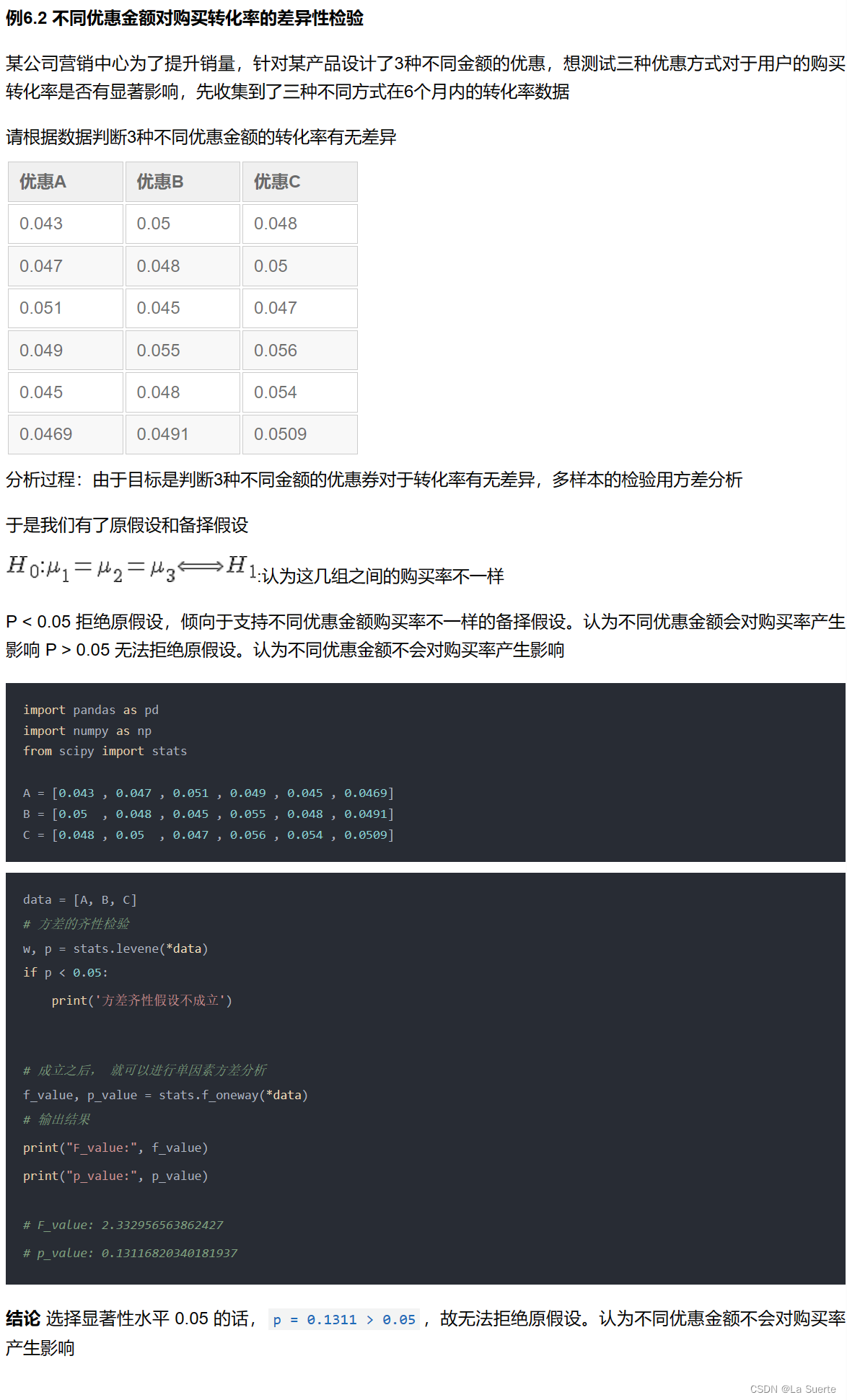
(b)例6.2
2)双因素方差分析
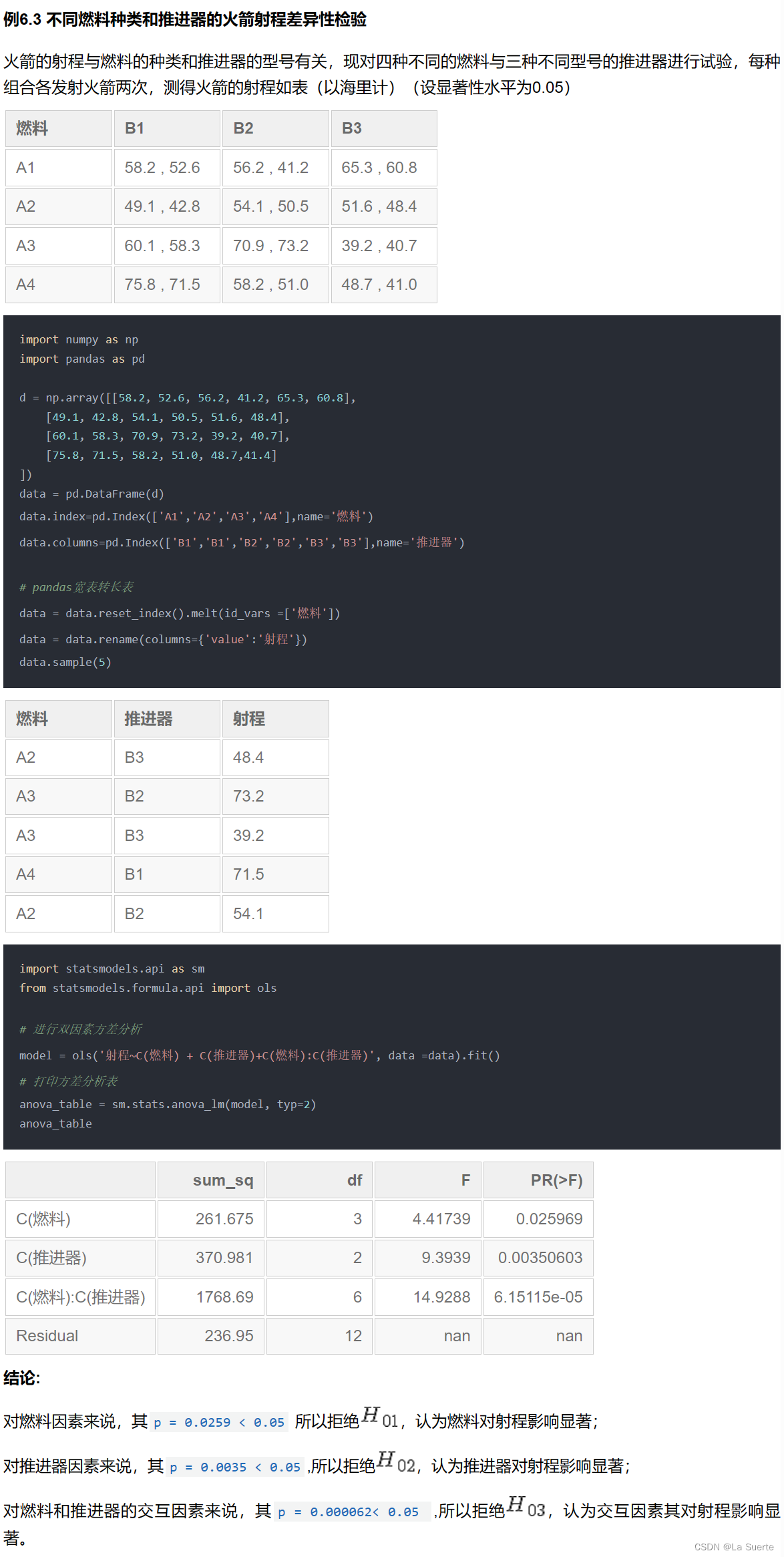
(a)等重复实验(例6.3)
(b)无重复实验(例6.4)
一. 差异性分析简介
1)差异性分析
差异性分析又称差异性显著检验,是假设检验的一种。它用于检测科学实验中实验组与对照组之间是否有差异以及差异是否显著的办法。
它判断样本间差异主要是随机误差造成的,还是本质不同。即:判断样本与总体所做的假设之间的差异是否是由于所做的假设与总体真实情况之间不一致所引起的,需要对数据进行显著性检验。
2)假设检验
使用假设检验需要设定原假设和备择假设。原假设通常是假设两个样本或总体之间没有显著差异,而备择假设则是与原假设相反的假设。
通过计算检验统计量和对应的p值来判断原假设是否成立:如果p值小于预设的显著性水平(通常为0.05),则拒绝原假设,认为两个样本或总体之间存在显著差异;否则,接受原假设,认为两个样本或总体之间没有显著差异。
3)差异性分析类型
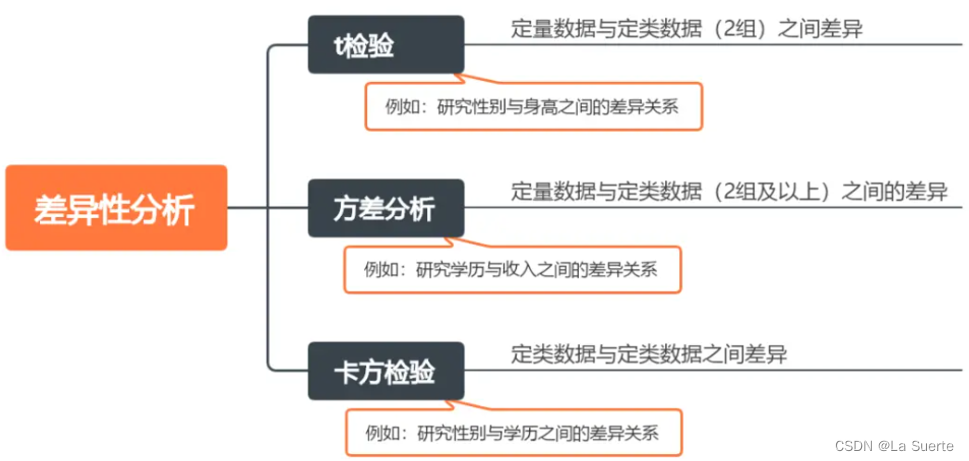
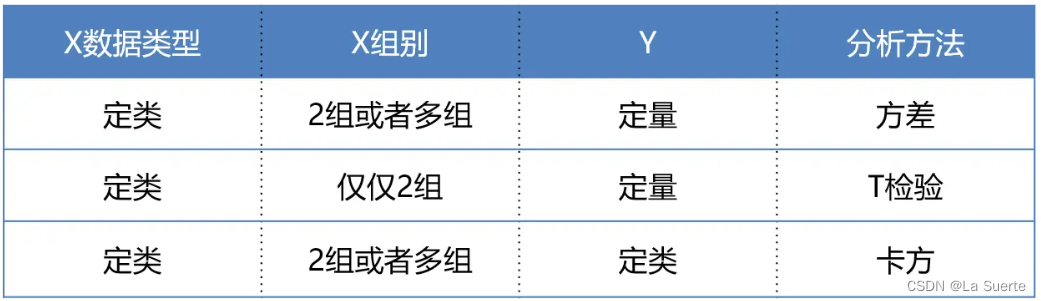
常用的差异性分析方法主要有三大类:t检验、方差分析、卡方检验。
- t检验(T-test):用于分析定类数据(仅2组)与定量数据之间的差异性
- 方差分析 (ANOVA):用于分析定类数据(2组及以上)与定量数据之间的差异性
- 卡方检验 (Chi-Square Analysis):用于分析定类数据与定类数据之间的差异性
二. 单个总体差异性的假设检验
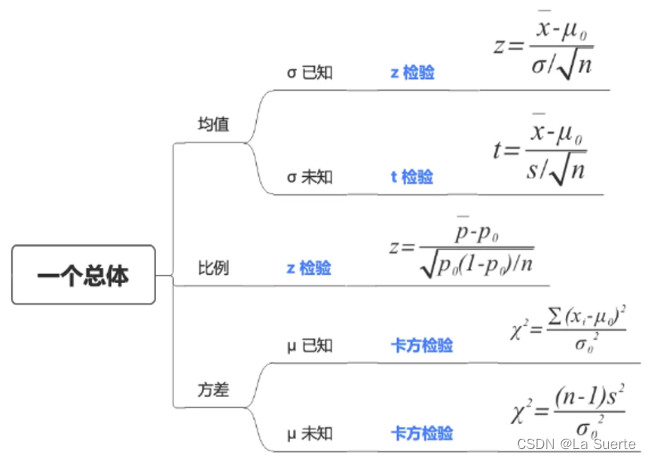
常见的单个总体差异性的假设检验分为3个类型:均值、比例、方差
1)单个总体均值
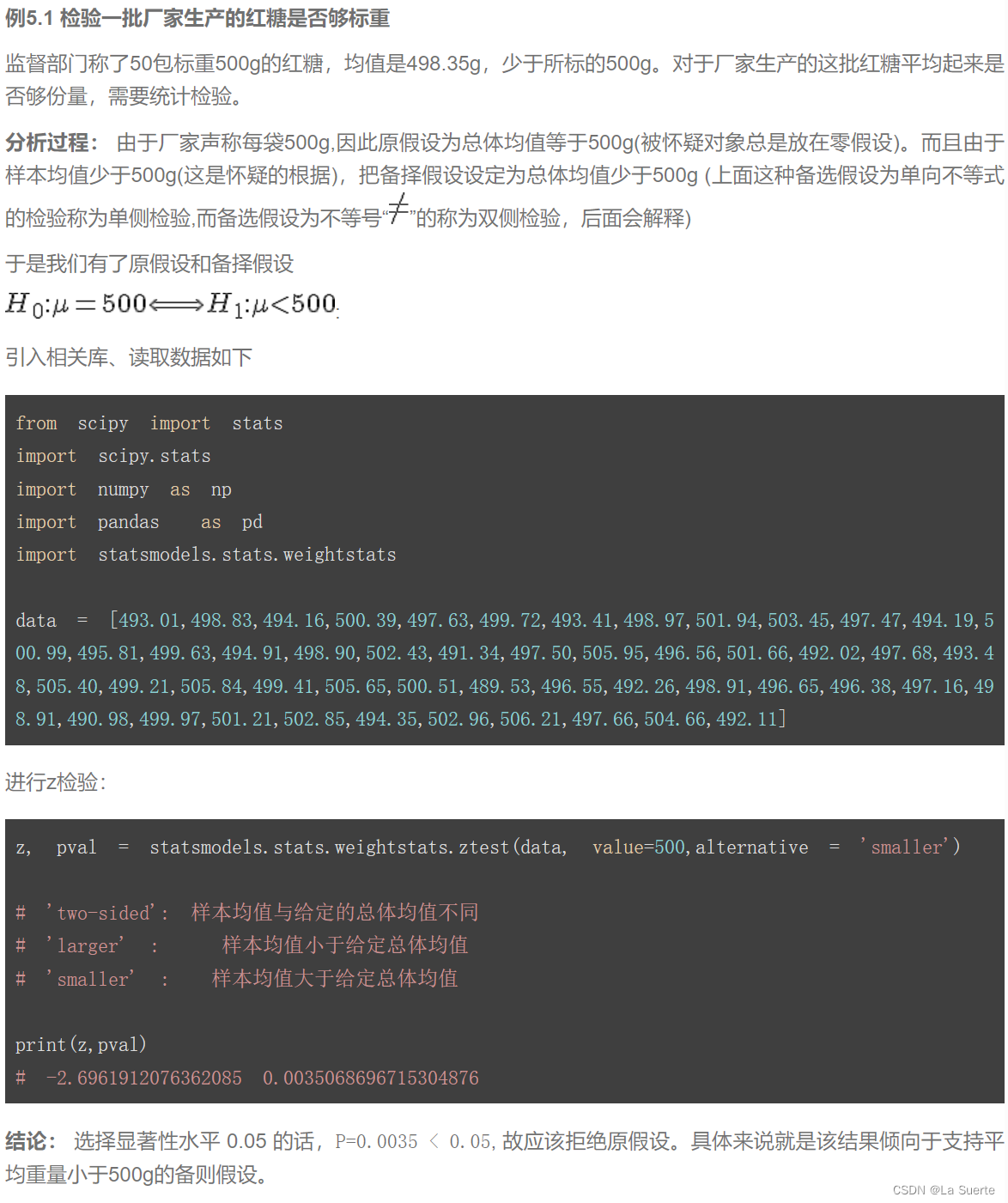
(a)σ已知的情况:z检验(例5.1)
(b)σ未知的情况:t检验(例5.2)
2)单个总体比例(例5.3)
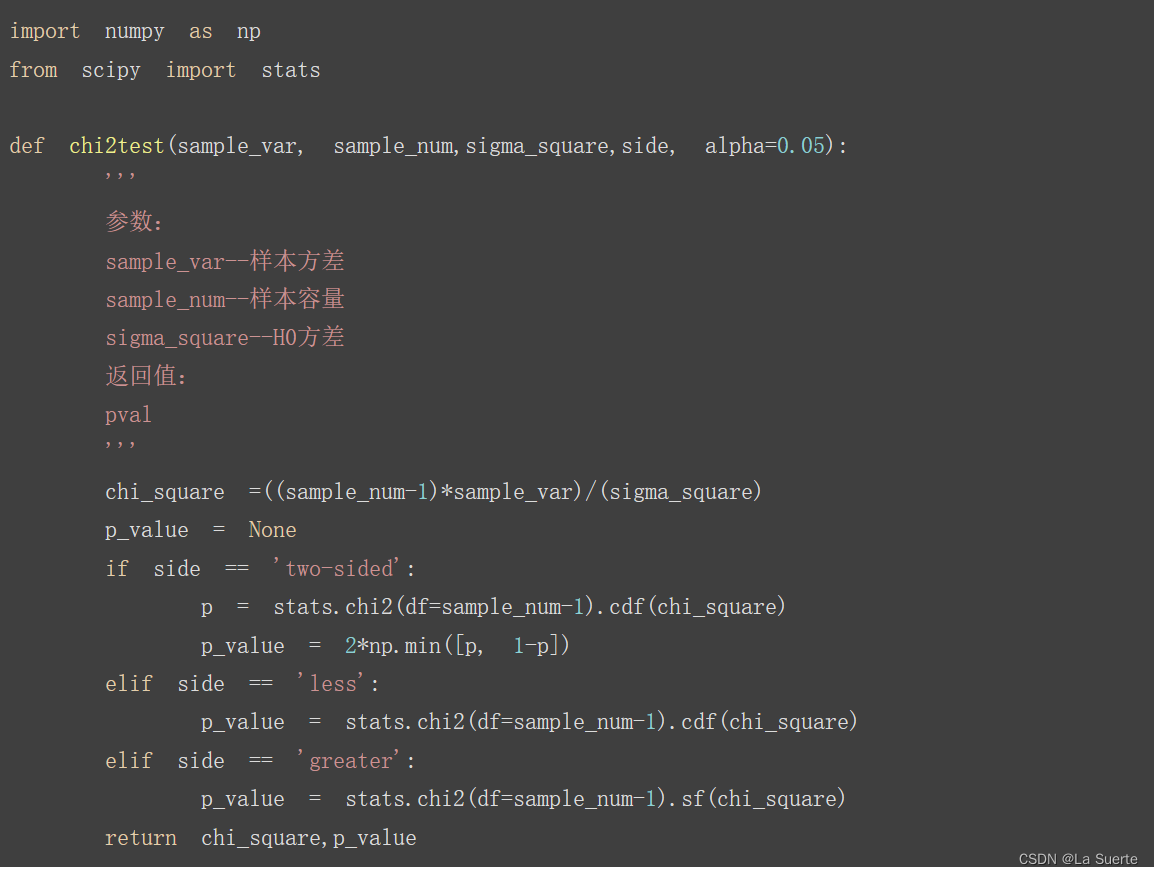
3)单个总体方差
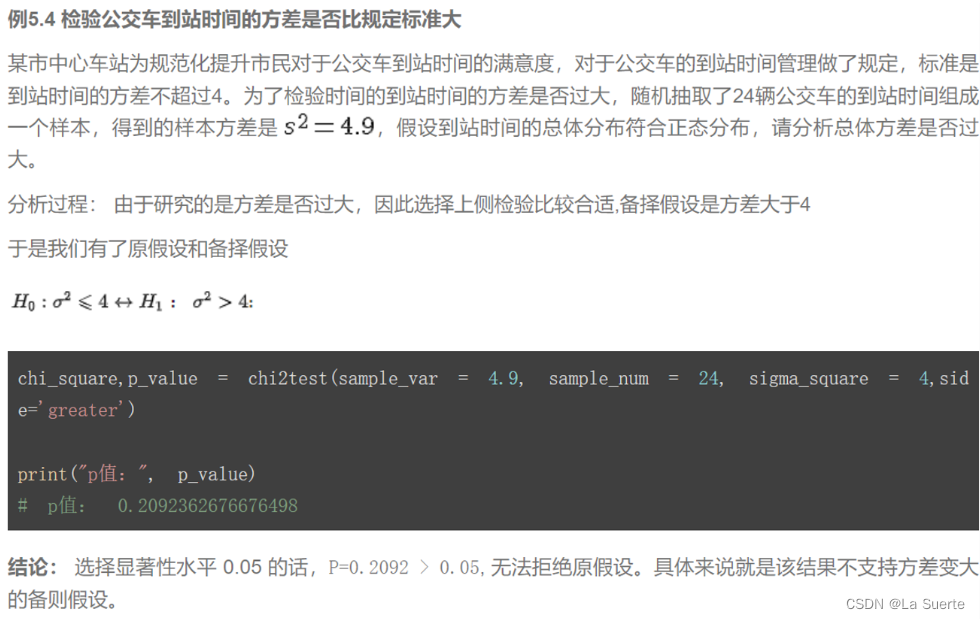
(a)例5.4
(b)例5.5
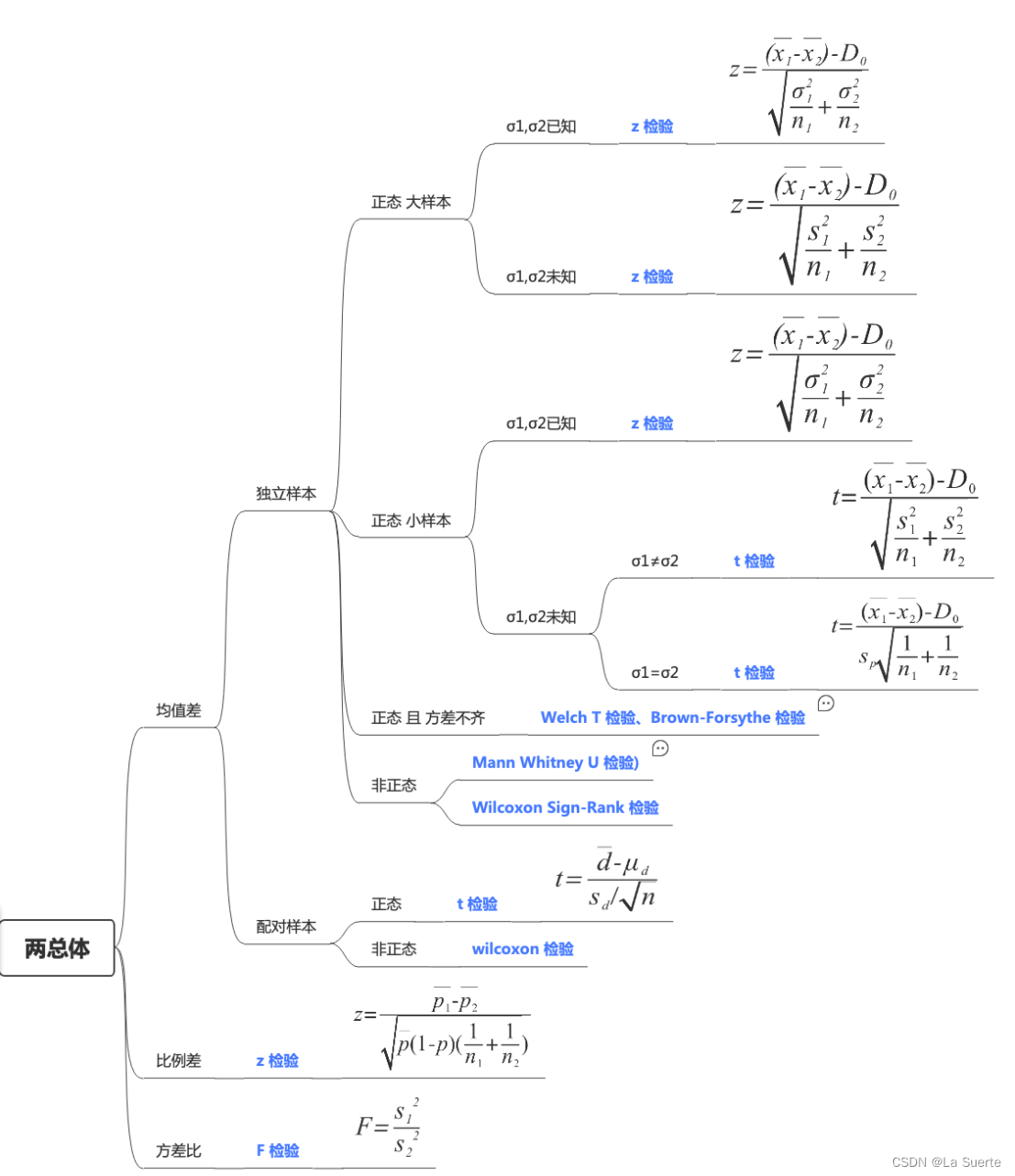
三. 两个总体差异性的假设检验
常见的两总体差异性的假设检验也分3个类型:均值、比例、方差
1)两总体均值之差
(a)独立样本(例5.6)
(b)配对样本(例5.7)
2)两总体比例之差(例5.8)
3)两总体方差之比
(b)例5.9
(c)例5.10
四. 方差分析
1)单因素多水平方差分析
(a)例6.1
(b)例6.2
2)双因素方差分析
在两因素实验中,两个因素不仅各自独立地对实验结果产生影响,而且因素与因素之间还可以联合对实验结果产生交互作用的影响。在无重复数的条件下,因为每种水平大配置进行一次实验,我们无法对交互作用进行分析,此时交互作用同实验的随机误差混合在一起,只能一起当做对记误差来考虑。
为了将两实验因素的交互作用同实验的随机误差分离,需要对两个因素的每一种不同水平搭配方式各进行若干次重复试验,才能看出两个因素之间是否存在交互作用。为了计算方便,常进行的是等重复的双因素实验。
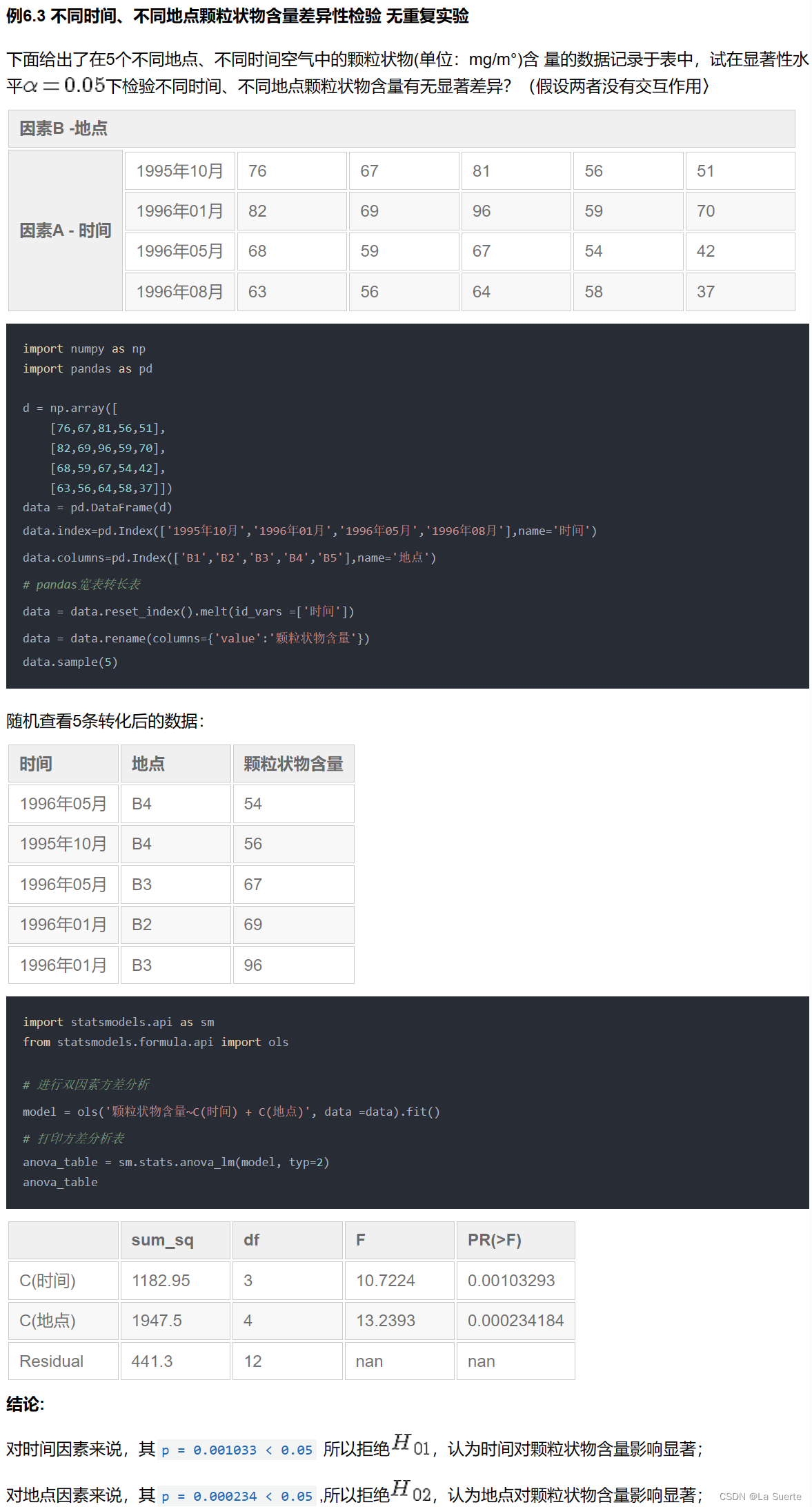
(a)等重复实验(例6.3)
等重复实验是指针对每个组合做大于等于两次的实验,比如下方例子中表里A1和B1的组合里面有2个数字,即说明做了两次实验,如果是3个数字刚说明次实验,依次类推。
(b)无重复实验(例6.4)
在等重复实验中,为了检验实验中两个因素的交互作用,需要针对每对组合至少要做2次以上实验,才能够将交互作用与误差分离开来。
而在处理实际问题时候,如果一直不存在交互作用,或者交互作用对实验指标影响极小,则可以不考虑交互作用,每对组合只做一次实验。
下一期:相关性分析,Bye!
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/151098.html