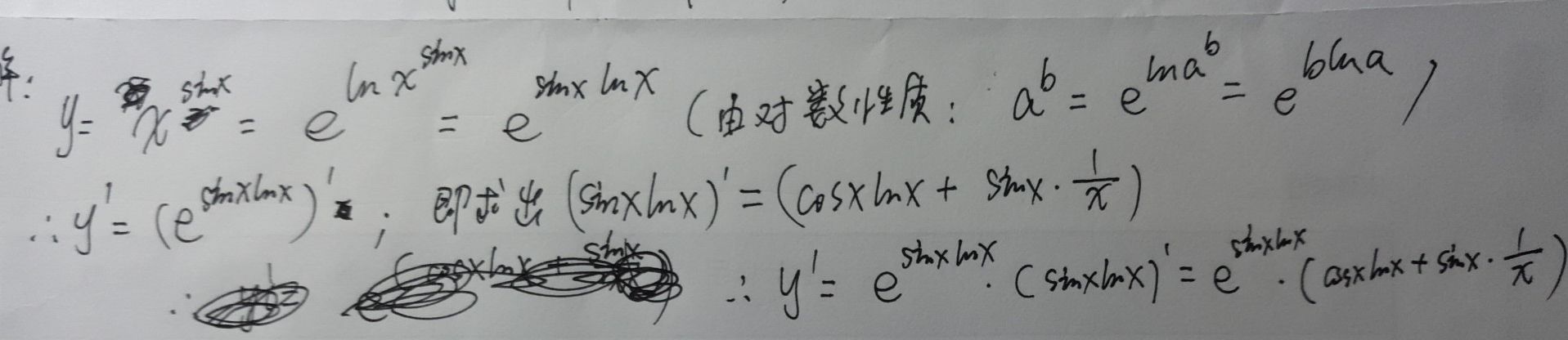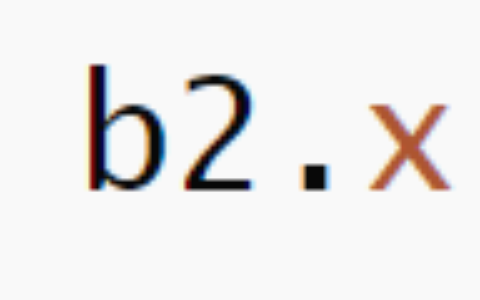本篇文章主要总结几种函数的求导方法。比如,反函数求导,隐函数求导,参数方程求导的方法。再简单讨论一下高阶导数的概念。
先看看考纲对这一块的要求:
3. 了解高阶导数的概念,会求简单函数的高阶导数. 4. 会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数. 考纲对这一块的要求主要是会求会用即可,因此我们主要是要熟悉其用法。
反函数求导:
前面我们已经介绍过反函数的概念。即y = f(x)上的所有的点(a, b)相对应的点(b, a)都在f-1(x)上存在。
反函数求导法则总结起来就是一句话:反函数的导数等于原函数导数的倒数。
我们可以用这个定理来证明一下反三角函数和对数函数的求导公式:
arctanx, arccosx, arccotx同理,所以反三角函数其实就不需要死记了,完全可以推出。
对数函数的导数公式推导:
这几种求导公式会证了之后,就大大减轻了我们的记忆负担。
隐函数求导:
一般我们遇到的函数比如:y = f(x)都是显函数。但是形如F(x, y) = 0;这种将x, y写成一个方程形式的,就是隐函数了。有时候我们可以直接将隐函数显化为显函数,这样的话就可以求导了。但是很多时候,不好显化,那如何对它求导呢?
我们一般是直接对等式两端的x求导。将y视为x的函数
比如这样一道题:
曲线C方程:x^2 + y^2 = 1;求在点x = 根号2 / 2, y = 根号2 / 2处,切线的方程。
这题显然不好直接显化,采用隐函数求导方法。
有了这个方法,我们可以对难以显化的函数求导了!
对数求导法:(求导大杀器!)
在它的面前,任何难求的导数都不是对手。
对数求导法是个求导技巧,它可以帮助我们求出许多难求的导数。
比如y = x ^ sinx 这种函数既不是幂函数,也不是指数函数,我们甚至无法用传统的求导公式求出它!
对数求导主要是利用了对数方便的计算,因为它可以把乘除化为加减,把幂化为乘除运算。
比如它有这些运算性质:
ln(a * b) = lna + lnb; ln(a / b) = lna - lnb; lna^b = b * lna; 比如我们现在来求y = x ^ sinx的导数:
结合一点复合函数的求导知识,直接秒掉了有木有!哈哈
我们再来求一个:
试想,如果没有对数的帮忙,这个求导过程将会非常复杂。
参数方程求导:
设x = u(t), y = v(t);
参数方程求导公式:dy/dx = (dy/dt) / (dx/dt)
即因变量与自变量各自对参数求导的比值。
首先对问题进行数学建模,t0处的运动方向就是曲线在t0处的切线,求出切线,这个方向就出来了,就是沿着切线方向嘛!
所以(1):
速度大小我们分解成Vx和Vy,即求出t0时刻水平方向上的速度大小和t0时刻竖直方向上的速度大小。这样的话,t0时刻的大小由勾股定理就能算出。
因为速度是位移对时间的变化率,即位移对时间的导数,所以水平方向上的速度是水平位移对时间的导数,竖直方向上的速度是竖直位移对时间的导数 。本题关键就是这里,深刻理解导数的物理意义。
那么:
说句题外话,在运算过程中,我们也发现,水平速度,即dx/dt,真的就是一个与时间没有关系的常数,它只和抛出的初速度和发射角度有关系。进一步验证了高中所学的物理知识
解决这种题,关键要能将实际问题进行数学建模,要知道导数就是变化率的意义!
相关变化率问题:
x, y之间存在某种函数关系,然后已知dx/dt,让我们求dy/dt的问题。
因为x,y之间存在函数关系,它们对于参数t的变化率,我们认为一定也存在某种关系。
关键也是要根据实际问题进行数学建模
仰角问题:
此题很明显速率是路程长度随时间的变化率(导数)。
要注意,仰角增加率是角度对时间的导数,这个可能不那么明显。
因此:
高阶导数
这一块考纲要求了解高阶导数的概念,会求简单的高阶导数即可。常见的几个函数的n阶导数要会求。
高阶导数说白了很简单,就是函数f(x)二阶及其二阶以上的导数(前提是该阶导数存在)。
定义:limx->x0 f'(x +x0) - f'(x) / x0
所以由定义,那么要求出某一个函数的n阶导数,我们要先知道它的n – 1阶导数。
这也是求高阶导数最直接的方法。
e^x的n阶导数:
因为e^x的每一阶导数都是
e^x自己,所以 它的n阶导数可以表示成: e^x
同理我们还可以求出sinx, lnx的n阶导数,这个要熟练:
高阶导数莱布尼茨公式:(可以求两个乘积形式的高阶导数)
公式形式类似于二项式定理
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/127786.html