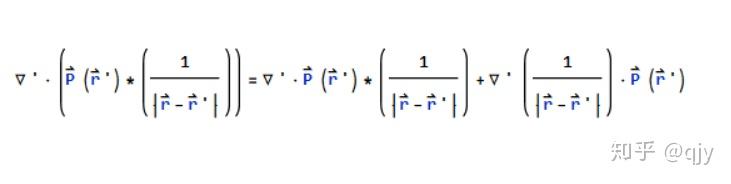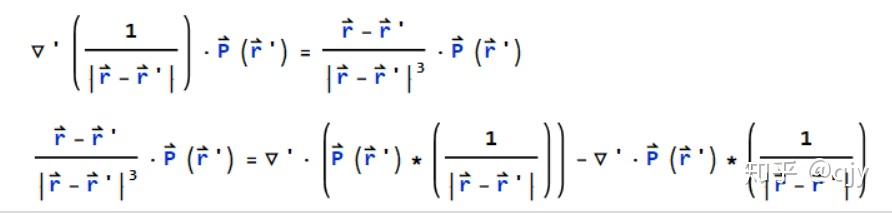电极化强度矢量与电位移矢量有什么实在意义吗？
学到这的时候感觉挺难理解的。。。。
电极化强度表明电介质在某一点单位体积的偶极矩。
电位移矢量，是我们构建的一个辅助场。
OK，建立一下线性电介质的物理描述，这里我第一次学的时候就迷糊的很，所以我打算写一下我建立思路的过程。
首先，怎么描述极化？我们先不考虑外场，只考虑一个纯粹的电极化的物体，怎样描述这个物体的电极化程度呢？用偶极矩！我们把极化电介质分为很多的偶极子，只要知道每一点的偶极矩，自然就求出了电势，从而求出电场，下面写出公式：
这是偶极矩的定义，已知偶极矩，求得偶极项电势的方法是：
偶极矩项贡献的电势
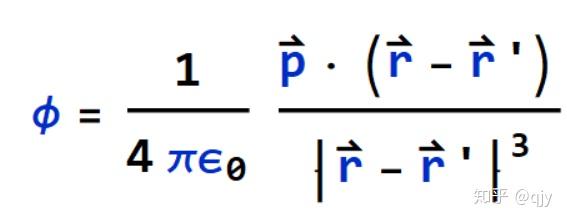
OK，你已经完全描述了一个电介质的电势场（所有偶极子的电势叠加），把它在连续的空间里求和，就要引入单位体积的偶极子，这就是电极化矢量，是不是很自然？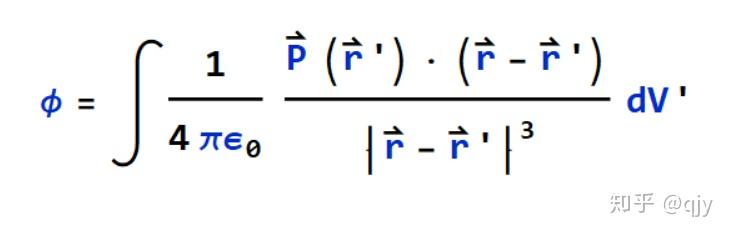
电介质极化贡献的电势
那现在，P矢量已经定义好了，再经过一点矢量分析，我们得到了结论，P矢量的散度是极化电荷体密度的负值。所以我们既可以认为是每一点的偶极子产生的电势，也可以认为是极化产生的净电荷产生的电势。但是两种不能同时用！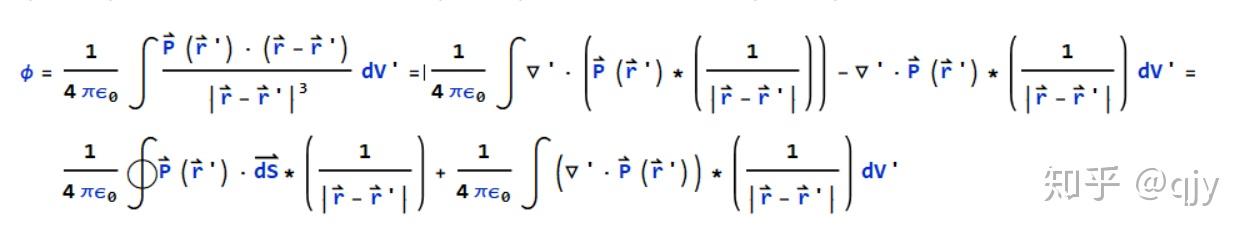
一点矢量分析后，物理意义也就明显了。注意过程中那个nabla是对源点而非对场点，因为P矢量是源点的函数，积分也是对源的积分
有了这个 的定义后，我们就开始琢磨， 是怎么来的呀？当然是电场造成的，最简单的模型是线性电介质，也就是 和 满足关系 ,这样，理论上给你一个随意形状的电介质你都应该知道怎么解出电场了！
接下来要做些数学上的简化，就如同另一位答主所说，和做辅助线一个道理：
这样的D的散度只和自由电荷有关，另外，D矢量场还可以与E有关联：
（只对于线性介质， 是介电常数）
这样，我们可以借用辅助场D知道E的散度，而不是直接求D。
根据矢量分析的一个定理，你知道一个矢量场的散度和旋度时，并且有一个边界条件，你就可以唯一确定这个场。而D的旋度不具有物理意义，不好计算，所以你不能直接求D场。不过引入这个辅助场的好处还是有的，比如
这就找到了E的的散度，另外在没有自由电荷的介质边界上， ，可以将其化作导数
是边界上的法矢，下标1和下标2对应不同介质。
如果你接触过泊松方程的话，你就知道，求解场的关键是求解电势的泊松方程。我们要求的量直接与E场相关，而D场只是辅助求一下边界条件之类的。
第一次写这么长，逻辑可能不太清晰，欢迎dalao提出宝贵意见
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/97541.html
