红黑树与普通的平衡二叉树除了颜色到底有什么区别?为什么要引入红黑树,它比普通的平衡二叉树究竟好在哪?
类似问题:红黑树比 AVL 树具体更高效在哪里?
一、摘要
二叉树,作为一种数据结构,在实际开发中,有着非常广泛的应用,尤其是以平衡二叉树、红黑树为代表,在前几篇文章中,我们详细的介绍了BST、AVL、RBT的算法以及代码实践,下面简要概括描述一下这三种树,以及它们之间的优劣。
二、BST
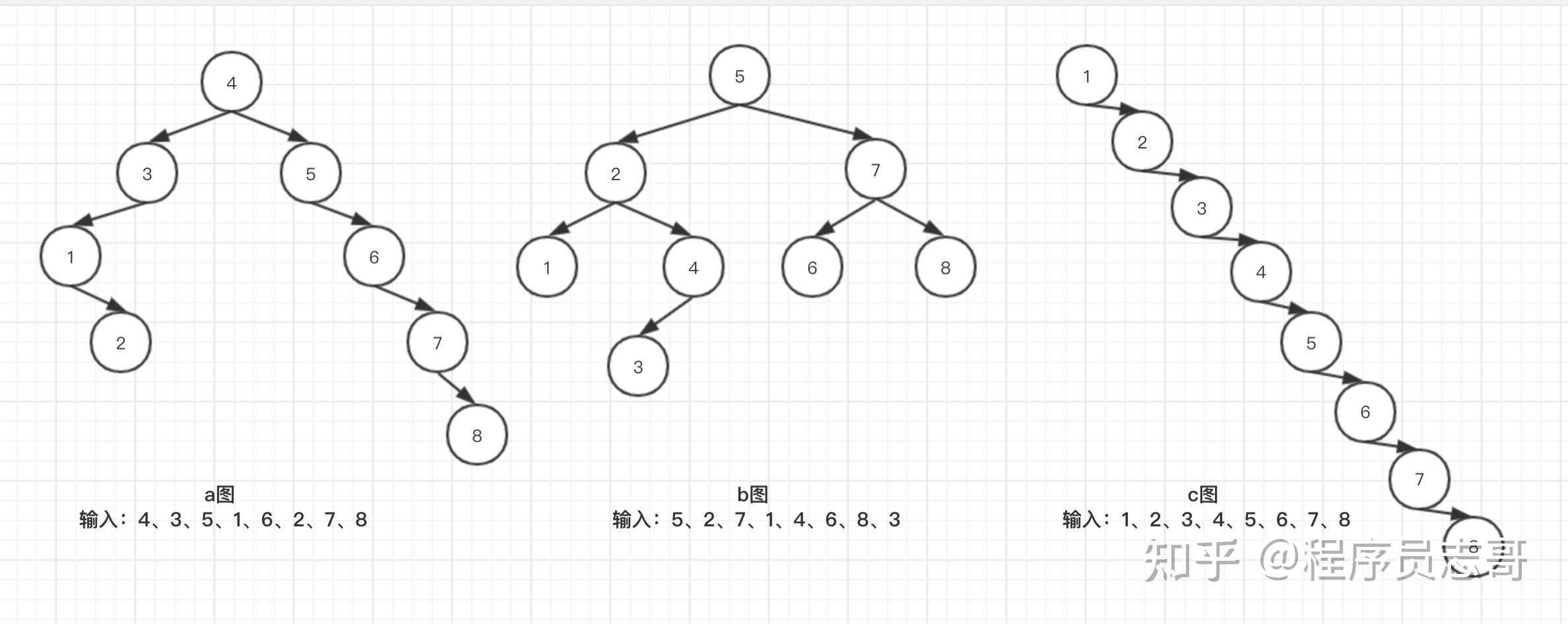
二叉查找树(英文全称:Binary Search Tree,简称:BST)是计算机科学中最早投入实际使用的一种树形结构,特性定义比较粗放(一个节点,最多2个分支),因此在树形形态结构上,有着多样,例如下图:
很明显,不同的形状,所需查找的次数是不一样的!
BST 的操作过程:查找操作:任何一个数据的查找过程都需要从根结点出发,沿某一个路径朝叶子结点前进,因此查找中数据比较次数与树的形态密切相关。
当树中每个结点左、右子树高度大致相同时,树高为logN,则平均查找长度与logN成正比,查找的平均时间复杂度在O(logN)数量级上。
当树形结构为一个单子树时,此时树高n,则平均查找长度为(n+1)/2,查找的平均时间复杂度在O(N)数量级上。插入操作:先通过查找方法找到合适的位置,然后将新结点插入到树的叶子上,完全不需要改变树中原有结点的组织结构。
插入一个节点的时间与查找一个插入合适的位置的时间完全相同。删除代价:当删除一个节点A,首先需要定位到这个节点A,这个过程需要一个查找的时间。然后根据树的形态分析,如果被删除结点的左、右子树只有一个存在,则改变形态的代价仅为O(1)。如果被删除结点的左、右子树均存在,只需要将A节点的左孩子的最末端的右子树或者A节点的右孩子的最末端的左子树结点与A互换,最后删除该节点即可。
删除操作的时间复杂度最大不会超过O(logN)。
BST效率总结:查找最好时间复杂度O(logN),最坏时间复杂度O(N)。插入、删除操作算法简单,时间复杂度与查找差不多。
更加详细的介绍,可以参阅下面这篇文章!程序员志哥:玩转二叉查找树
三、AVL
二叉查找树在最差情况下和顺序查找效率相当,这点是无法忍受的。
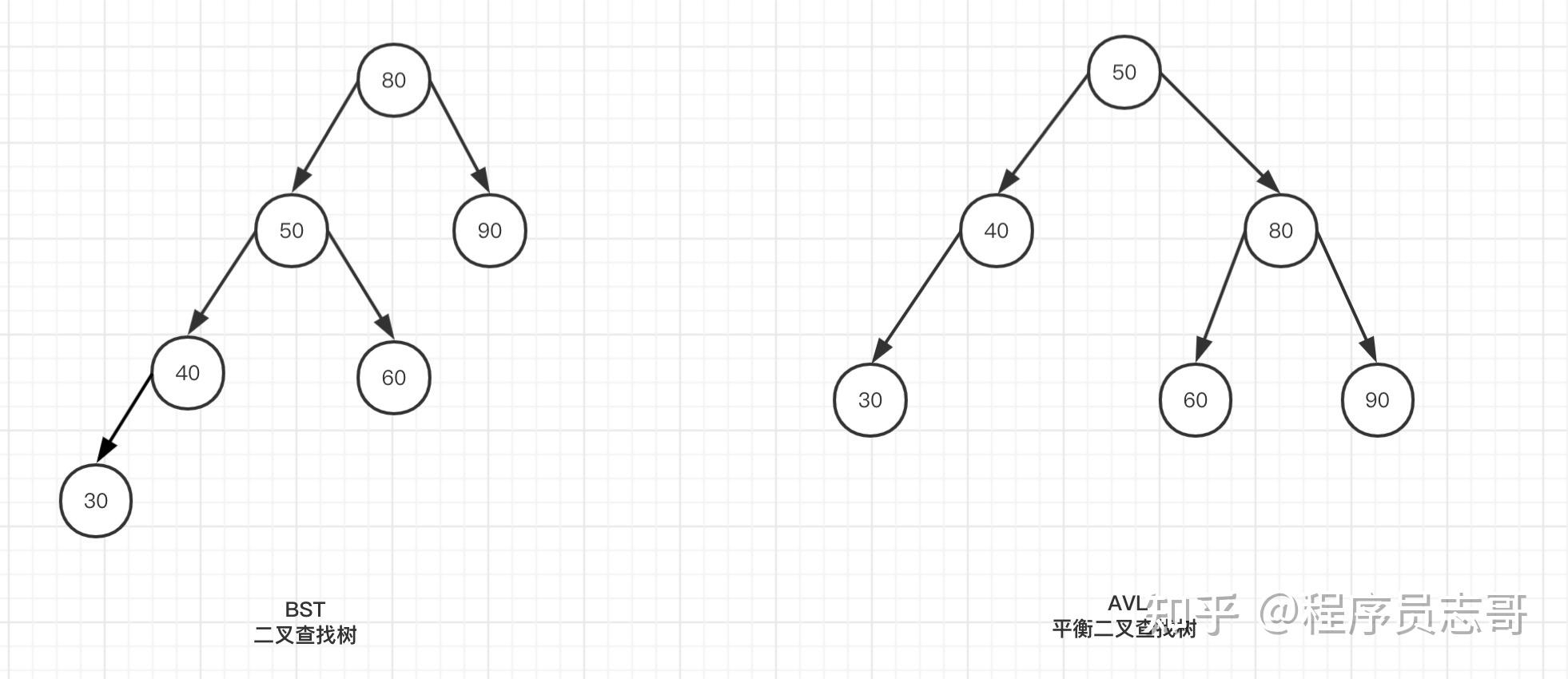
平衡二叉查找树的出现,主要是为了解决当二叉树查找树形态结构变成一个链条结构的时候,查找效率变低的问题,算法由和两位大神发明,同时也俗称树,特性如下:它的左子树和右子树都是平衡二叉树;且它的左子树和右子树的深度之差的绝对值(平衡因子 ) 不超过1;
简单的说,就是为了保证平衡,当前节点的左子树、右子树的高度差不超过1!
当树的左、右子树高度超过差超过1时,核心就是通过左旋转、右旋转实现树再次高度平衡。
AVL 的操作过程:查找操作:AVL是严格平衡的BST(平衡因子不超过1)。查找过程与BST一样,只是AVL不会出现最差情况的BST(单支树)。因此查找效率最好,最坏情况都是O(logN)数量级的。 插入操作:AVL插入与BST思路一样,不同的是AVL必须要保证严格平衡(),每一次插入数据使得AVL中某些结点的平衡因子超过1就必须进行旋转操作。事实上,AVL的每一次插入结点操作最多只需要旋转1次(单旋转或双旋转)。因此,总体上插入操作的代价仍然在O(logN)级别上(插入结点需要首先查找插入的位置)。 删除操作:AVL删除结点的算法与BST思路一样,但是删除之后必须检查从删除结点开始到根结点路径上的所有结点的平衡因子。因此删除的代价稍微要大一些。每一次删除操作最多需要O(logN)次旋转。因此,删除操作的时间复杂度为O(logN)+O(logN)=O(2logN)。
AVL 效率总结:查找的时间复杂度维持在O(logN),不会出现最差情况。AVL树在执行每个插入操作时最多需要1次旋转(单旋转或双旋转),其时间复杂度在O(logN)左右。AVL树在执行删除时代价稍大,执行每个删除操作的时间复杂度需要O(2logN)。
更加详细的介绍,可以参阅下面这篇文章!程序员志哥:什么是 AVL 树?
四、RBT
平衡二叉查找树通过严格平衡策略以牺牲建立查找结构的代价,换来了稳定的查找时间复杂度。但是相对来说,在删除方面,时间复杂度稍大。
于是就出现了平衡二叉B树,后来,在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的红黑树。
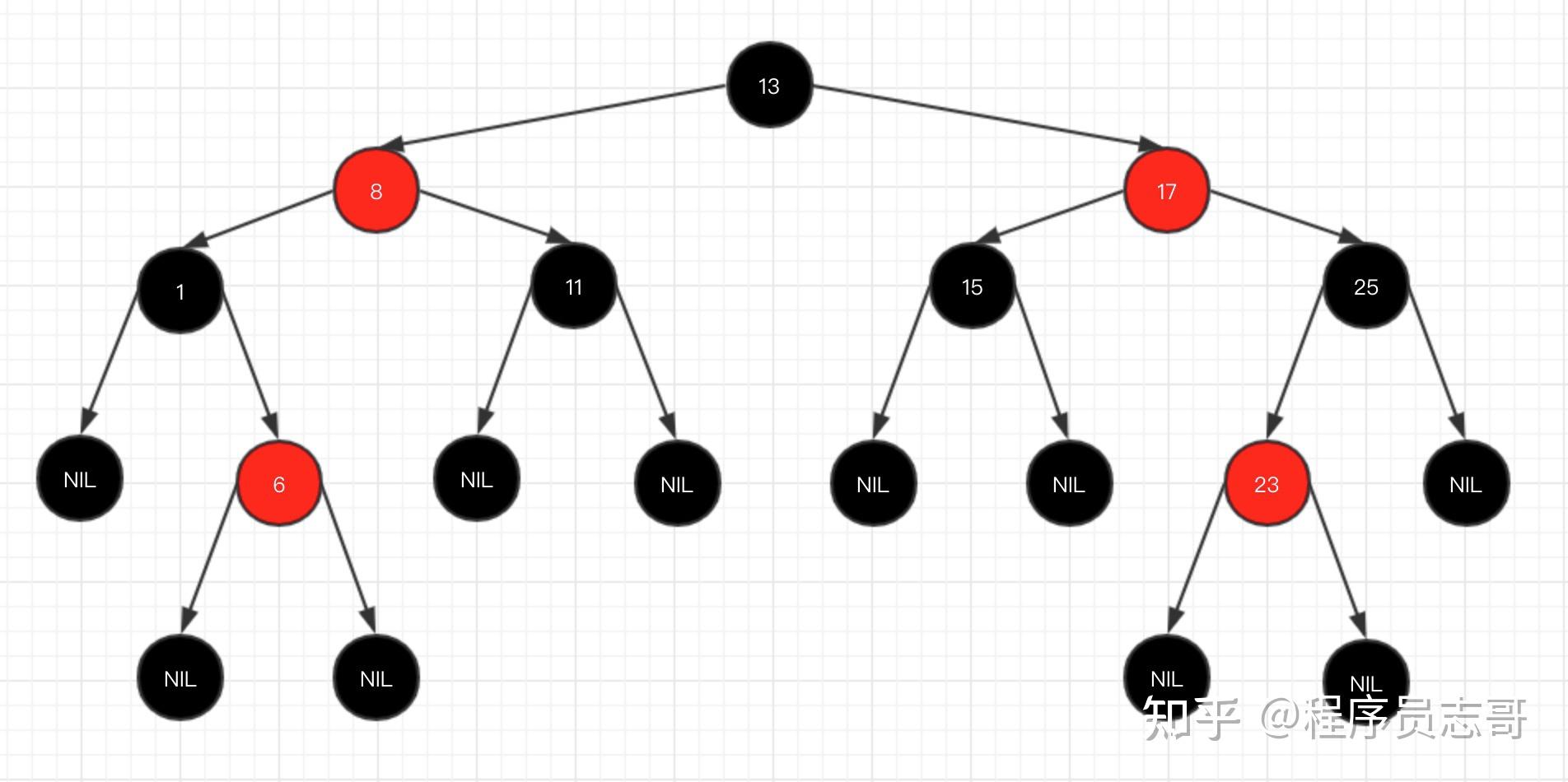
红黑树(英文全称:red-black-tree,简称:RBT),特性如下:1.每个节点要么是黑色要么是红色;2.根节点是黑色;3.每个叶子节点是黑色;(注意:这里叶子节点,是指为空的叶子节点)4.如果一个节点是红色的,则它的子节点必须是黑色的;(说明父子节点之间不能出现两个连续的红节点)5.从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点;
确保没有一条路径会比其他路径长出俩倍,因而,红黑树是相对的接近平衡的二叉树,但是相比平衡二叉树而言,尤其是删除的时间复杂度,有所降低。
RBT 的操作过程:查找操作:由于红黑树的性质(最长路径长度不超过最短路径长度的2倍),可以说明红黑树虽然不像AVL一样是严格平衡的,但平衡性能还是要比BST要好。其查找代价基本维持在O(logN)左右,但在最差情况下(最长路径是最短路径的2倍少1),比AVL要略逊色一点。 插入操作:RBT插入结点时,需要旋转操作和变色操作。但由于只需要保证RBT基本平衡就可以了。因此插入结点最多只需要2次旋转,这一点和AVL的插入操作一样。虽然变色操作需要O(logN),但是变色操作十分简单,代价很小。 删除代价:RBT的删除操作代价要比AVL要好的多,删除一个结点最多只需要3次旋转操作。
RBT 效率总结:查找效率最好情况下时间复杂度为O(logN),但在最坏情况下比AVL要差一些,但也远远好于BST。插入和删除操作改变树的平衡性的概率要远远小于AVL(RBT不是高度平衡的)。因此需要的旋转操作的可能性要小,而且一旦需要旋转,插入一个结点最多只需要旋转2次,删除最多只需要旋转3次(小于AVL的删除操作所需要的旋转次数)。虽然变色操作的时间复杂度在O(logN),但是实际上,这种操作由于简单所需要的代价很小。
更加详细的介绍,可以参阅下面这篇文章!程序员志哥:图解红黑树实现过程
五、总结
平衡二叉查找树、红黑树,在查询、插入、删除操作方面都是基于二叉查找树的算法思路,不同点是:插入、删除之后的调整过程,平衡二叉查找树主要是通过左旋转、右旋转实现树高度再次平衡,而红黑树因为引进了颜色,相比平衡二叉查找树,多了一个颜色转换操作。
三者整体比较,红黑树要优于平衡二叉查找树,远优于二叉查找树!
最近,很多读者咨询我,有没有相关的面试题资源,针对网友的要求,特整理了一堆的干活,整个面试资料包分 9 个文件夹,在此分享给大家!点击下方地址即可!
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/94836.html