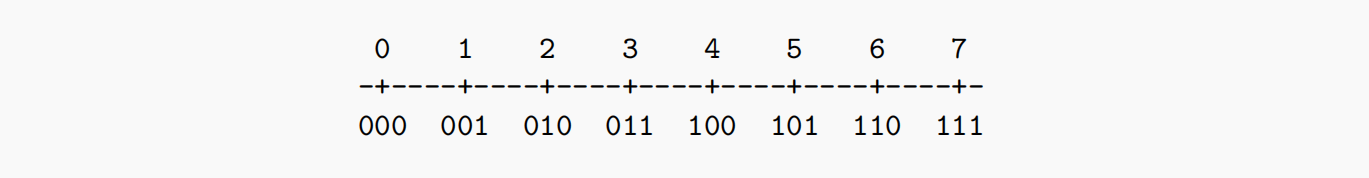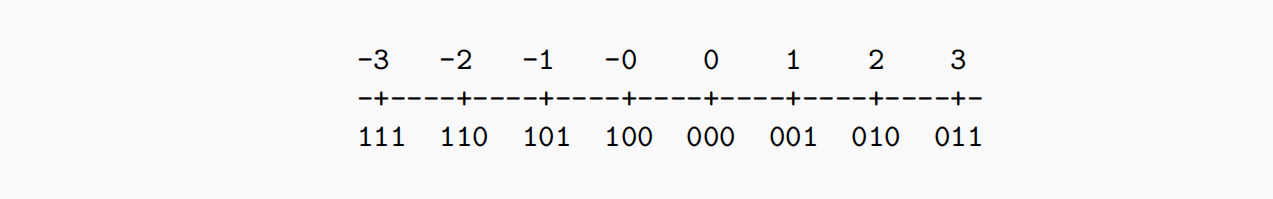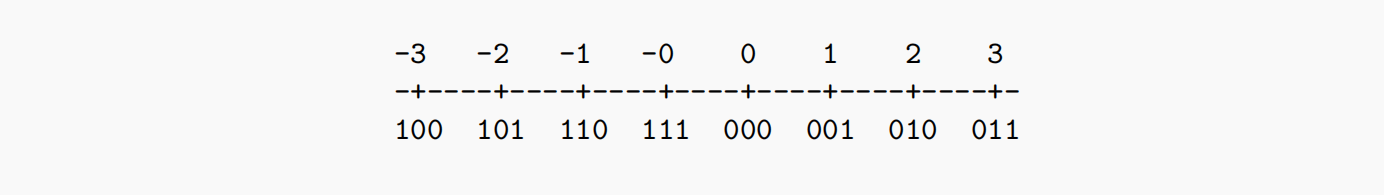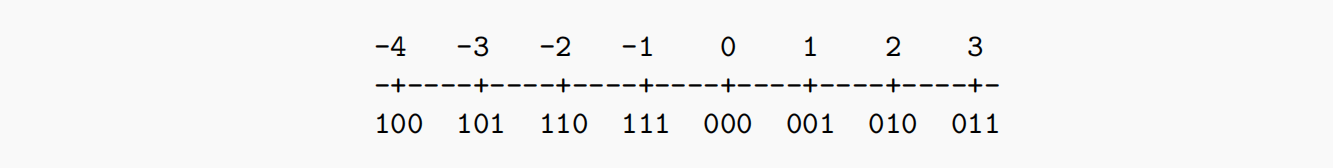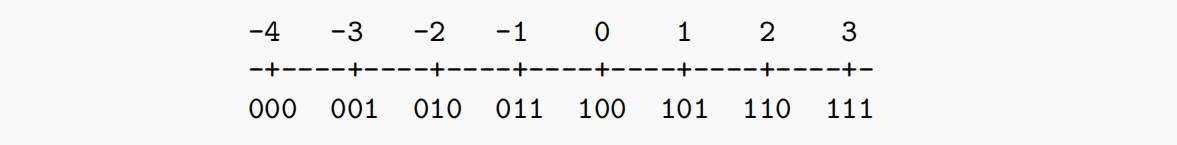离散时域滤波器的实现（四）有限字长表示与误差分析
当鲜花凋零遍地，是否有新的种子在萌芽？
一、回顾
上节总结了FIR系统的结构设计。Michael Lieman：离散时域滤波器的实现（三）FIR系统的实现
自此，理论原理已经了解完毕，接下来要进入到计算机实际运算过程中，出现的有限字长表示等概念及其带来的量化误差对LTI系统的影响。
二、有限精度数值效应概览
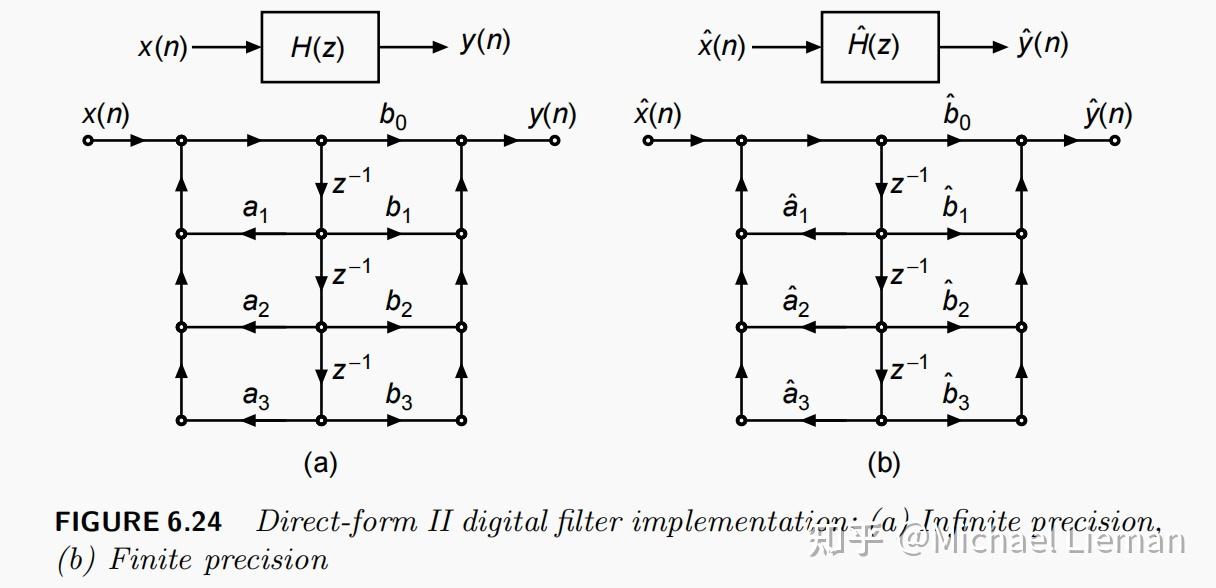
当在滤波器实现中使用有限精度表示时，有三个可能的考虑因素会影响其输出的整体质量：对滤波器参数 
数值化成 对输入序列 数值化成 对输出序列 数值化成
示意图如下：
我们首先讨论计算机中的数字表示，这导致了数字量化的过程和由此产生的误差表征。
然后分析滤波器系数量化对数字滤波器频率响应的影响。
乘法和加法量化(统称为算术舍入误差)对滤波器输出的影响将在第10章中讨论。
2.1. 数字的表示
众所周知，计算机中使用二进制比特来表示实数。根据信号处理中所要求的复杂度和精确度，有两种方式实现：
定点(fixed-point)数和浮点(floating-point)数。前者容易实现，但是所能表示的数值大小范围固定。而后者较难
实现，但是具有动态的表示范围。
此外，由于计算机只能储存二进制比特，因此对于负数的表示，出现了三种不同的方法，分别为
原码 sign-magnitude format；
反码 one’s-complement format；
补码 two’s-complement format；
余码 excess-2B−1 format 。
下面我们来看具体内容。
2.2.定点数表示
我们知道
对于正数而言，B位比特数可以表示 之间的正整数。
举例如下：
2.2.1.原码：
第一位作为符号位，之后为绝对值，可以表示 .
示例如下：
2.2.2.反码：
对正值全部取反，即得负值。可以表示 .
举例如下：
缺点：对于0存在两种表示方法，加法的实现稍显复杂。
2.2.3.补码：
对正值取反后再加一，得到负值。可以表示 .
优点：0只有一种表示形式，增加了一个负数表示。正数的补码是负数，负数的补码刚好是原来的正数。统一了加法和减法。在一定的范围内，两个正数相加得到正结果，两个负数相加得到负结果。
举例如下：
2.2.4.余码：
满足
举例如下：
2.3.一般定点数表示
前面所能够表示的只有正数，我们可以扩展到有限精度实数。其一般表示为
共有 位字长。由1个符号位，L个整数位，B个分数位构成。
2.4.浮点数表示
现在我们考虑一些数量级比较大的数，如果使用定点数表示法，需要极大的字长，然而在物理现实中，这种数的精度并不高，因此我们联想到科学计数法来表示大数：
对于二进制浮点数，我们规定指数采用L位余码格式表示；规范化：小数点后紧跟1，共B位小数（ ）。
即 要注意，左侧的E代表指数部分。
优点：具有很大的动态范围，并且分辨率(定义为两个连续可表示的水平之间的间隔)与幅度成正比。
缺点：没有数字0的表示，而且算术运算比定点表示更复杂。注意：以上只是本书自定义的一种简化表达形式，只在本书中用于简化讨论，真正现实中通用的浮点数表示是IEEE-754标准。
三、误差和量化特性处理
3.1.基本量化方法
一般来讲，量化过程有去尾，舍入两种方法，一般而言，采用舍入的方法，显然，对于1+L+B位表示，量化相对误差为 。
而对于IEEE-754浮点表示法而言，相对误差为 .
3.2. 滤波器参数的量化
3.2.1. 对零极点的影响
我们考虑传递函数分母：
通过计算得出极点受到系数变化而产生的变化可以表示为
从中可以看到当极点之间的距离离得越近时，因系数的量化误差而受到的影响越大。
利用这一点，我们可以得到以下重要结论：1. 级联形式结构比直接形式结构具有更好的有限字长特性。这是因为级联形式可以避免极点靠得太近的情况。
如下图所示：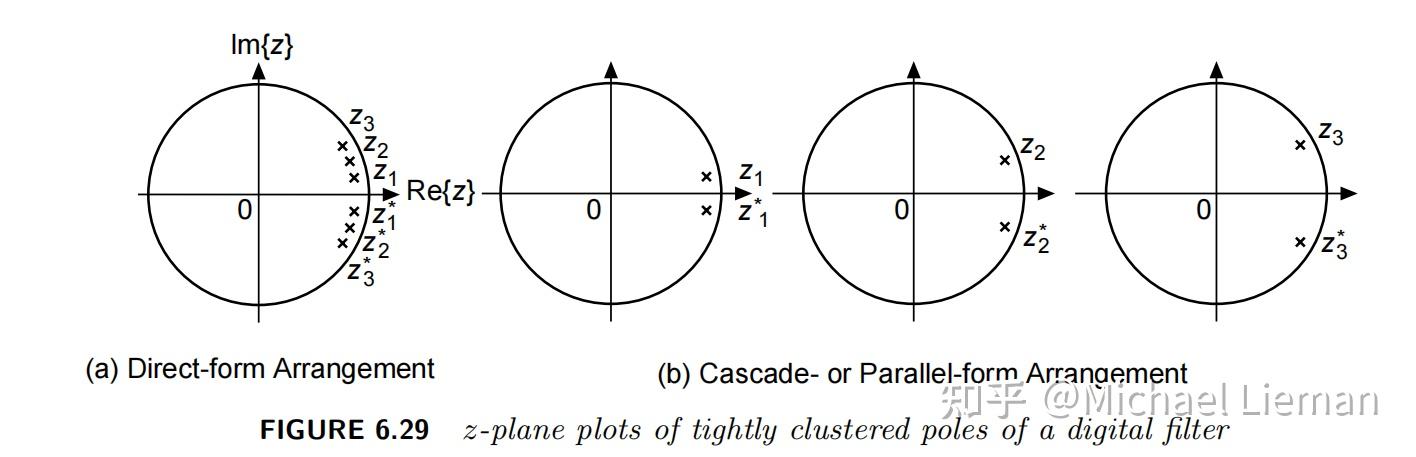
2. 并联结构误差最小，性能最好。因为各个子系统相互独立，相互之间不受影响。
四、相关代码
3.1.反码
3.2.补码
五、预告
之后进入第七章FIR滤波器设计。
激活谷谷主为您准备了激活教程，为节约您的时间请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/97457.html
