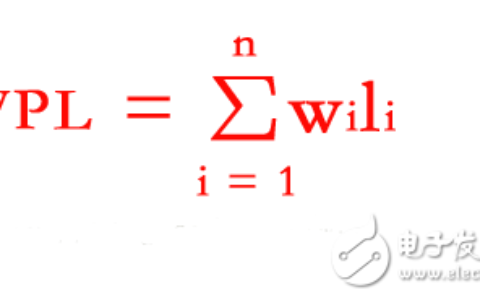一天一个数据结构知识——哈夫曼树
在了解哈夫曼树之前我们要了解三个概念:结点的权值,结点的带权路径长度,树的带权路径长度。节点的带权路径长度就是结点的权值乘以路径长度;树的带权路径长度就是树的所有叶结点的带权路径长度之和。而哈夫曼树就是带权路径长度最小的树,也叫做最优二叉树。
那么怎么构造哈夫曼树呢?首先在所有节点中选择两个权值最小的节点,作为兄弟节点,这两个节点的权值之和就是他们根节点的权值,然后再在所有节点中选择两个根节点最小的树作为兄弟节点以此类推。通过这样的方法,可以保证该树有一下几个性质:首先初始的几个节点都将成为树的叶结点,节点的权值越小,其距离根节点的距离越远。并且哈夫曼树的节点总数为2n-1。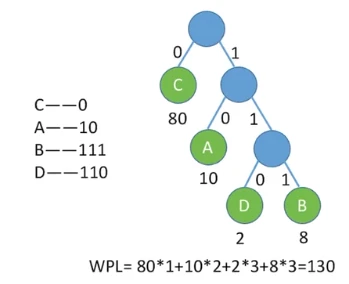
哈夫曼树的诞生使得哈夫曼编码应运而生,如果我们用0/1来表示数据,那么通过哈夫曼编码,可以使权值高的数据用较少的字节表示出来,这就是可变长度编码。并且哈夫曼编码可以有效避免解码时产生的歧义,因为哈夫曼编码是一种前缀编码,也就是没有一个编码是另一个编码的前缀。这样哈夫曼树的带权路径长度就变成哈夫曼编码的传输字节数(叶子节点的权值就是要传输字符集中字符的频度)。我们熟悉的摩尔斯电码也体现出哈夫曼编码思想,在英文中出现频率越高的字母摩斯电码越简单,现如今哈夫曼编码已经广泛应用于数据压缩。
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/95927.html