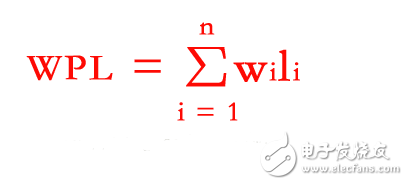哈夫曼树基本概念与构造 – 全文
哈夫曼树中的名词意思
树的权值:每个树节点所在的那个数字。
路径:两个节点之间所经过的分支。
路径长度: 某一路径上的分支条数。
节点带权路径长度: 节点的权值*该节点的路径长度。
树带权路径长度:所有叶子节点的带全路径长度之和。
树带权路径长度:所有叶子节点的带全路径长度之和。
1、基本概念
a、路径和路径长度
若在一棵树中存在着一个结点序列 k1,k2,……,kj, 使得 ki是ki+1 的双亲(1《=i《j),则称此结点序列是从 k1 到 kj 的路径。
从 k1 到 kj 所经过的分支数称为这两点之间的路径长度,它等于路径上的结点数减1.
b、结点的权和带权路径长度
在许多应用中,常常将树中的结点赋予一个有着某种意义的实数,我们称此实数为该结点的权,(如下面一个树中的蓝色数字表示结点的权)
结点的带权路径长度规定为从树根结点到该结点之间的路径长度与该结点上权的乘积。
c、树的带权路径长度
树的带权路径长度定义为树中所有叶子结点的带权路径长度之和,公式为:
其中,n表示叶子结点的数目,wi 和 li 分别表示叶子结点 ki 的权值和树根结点到 ki 之间的路径长度。
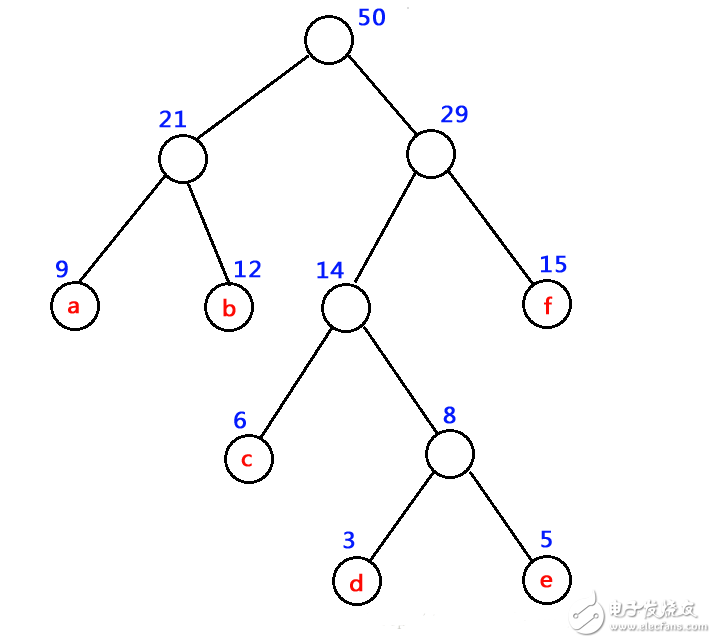
如下图中树的带权路径长度 WPL = 9 x 2 + 12 x 2 + 15 x 2 + 6 x 3 + 3 x 4 + 5 x 4 = 122
d、哈夫曼树
哈夫曼树又称最优二叉树。它是 n 个带权叶子结点构成的所有二叉树中,带权路径长度 WPL 最小的二叉树。
如下图为一哈夫曼树示意图。
哈夫曼树的构造
根据哈弗曼树的定义,一棵二叉树要使其WPL值最小,必须使权值越大的叶子结点越靠近根结点,而权值越小的叶子结点越远离根结点。
哈弗曼依据这一特点提出了一种构造最优二叉树的方法,其基本思想如下:
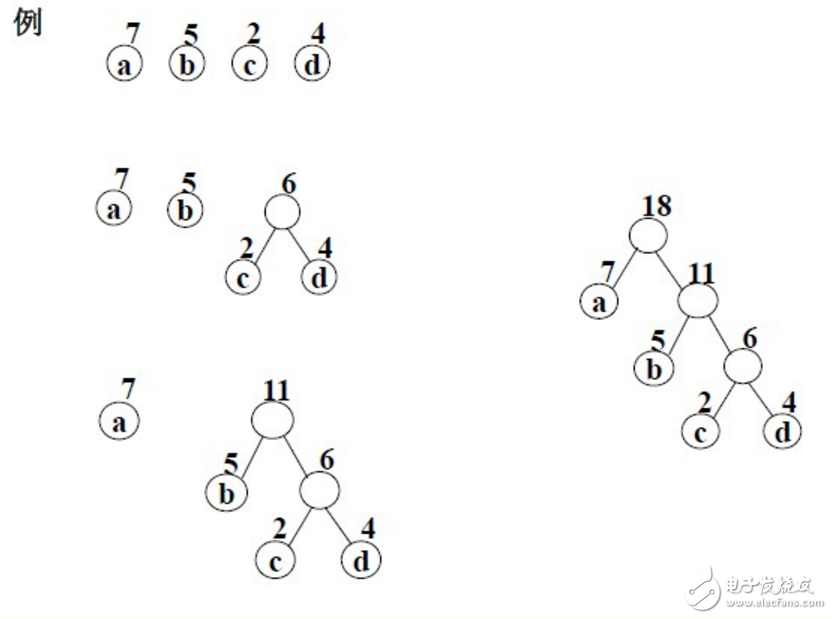
下面演示了用Huffman算法构造一棵Huffman树的过程:
假设有n个权值,则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn,则哈夫曼树的构造规则为:
(1) 将w1、w2、…,wn看成是有n 棵树的森林(每棵树仅有一个结点);
(2) 在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;
(3)从森林中删除选取的两棵树,并将新树加入森林;
(4)重复(2)、(3)步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树。
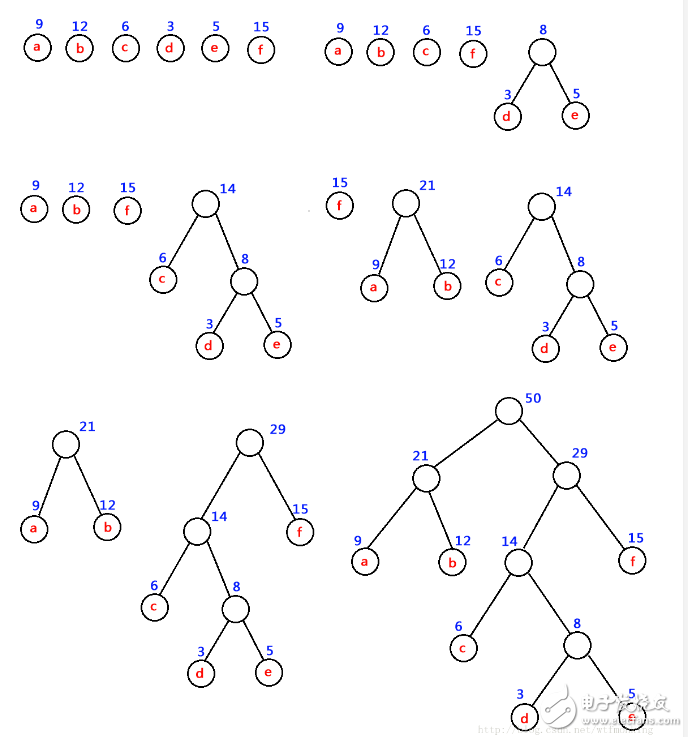
如:对 下图中的六个带权叶子结点来构造一棵哈夫曼树,步骤如下:
注意:为了使得到的哈夫曼树的结构尽量唯一,通常规定生成的哈夫曼树中每个结点的左子树根结点的权小于等于右子树根结点的权。
具体算法如下:
//2、根据数组 a 中 n 个权值建立一棵哈夫曼树,返回树根指针
struct BTreeNode* CreateHuffman(ElemType a[], int n)
{
int i, j;
struct BTreeNode **b, *q;
b = malloc(n*sizeof(struct BTreeNode));
for (i = 0; i 《 n; i++) //初始化b指针数组,使每个指针元素指向a数组中对应的元素结点
{
b[i] = malloc(sizeof(struct BTreeNode));
b[i]-》data = a[i];
b[i]-》left = b[i]-》right = NULL;
}
for (i = 1; i 《 n; i++)//进行 n-1 次循环建立哈夫曼树
{
//k1表示森林中具有最小权值的树根结点的下标,k2为次最小的下标
int k1 = -1, k2;
for (j = 0; j 《 n; j++)//让k1初始指向森林中第一棵树,k2指向第二棵
{
if (b[j] != NULL && k1 == -1)
{
k1 = j;
continue;
}
if (b[j] != NULL)
{
k2 = j;
break;
}
}
for (j = k2; j 《 n; j++)//从当前森林中求出最小权值树和次最小
{
if (b[j] != NULL)
{
if (b[j]-》data 《 b[k1]-》data)
{
k2 = k1;
k1 = j;
}
else if (b[j]-》data 《 b[k2]-》data)
k2 = j;
}
}
//由最小权值树和次最小权值树建立一棵新树,q指向树根结点
q = malloc(sizeof(struct BTreeNode));
q-》data = b[k1]-》data + b[k2]-》data;
q-》left = b[k1];
q-》right = b[k2];
b[k1] = q;//将指向新树的指针赋给b指针数组中k1位置
b[k2] = NULL;//k2位置为空
}
free(b); //删除动态建立的数组b
return q; //返回整个哈夫曼树的树根指针
}
哈夫曼树的在编码中的应用
在电文传输中,需要将电文中出现的每个字符进行二进制编码。在设计编码时需要遵守两个原则:
(1)发送方传输的二进制编码,到接收方解码后必须具有唯一性,即解码结果与发送方发送的电文完全一样;
(2)发送的二进制编码尽可能地短。下面我们介绍两种编码的方式。
1. 等长编码
这种编码方式的特点是每个字符的编码长度相同(编码长度就是每个编码所含的二进制位数)。假设字符集只含有4个字符A,B,C,D,用二进制两位表示的编码分别为00,01,10,11。若现在有一段电文为:ABACCDA,则应发送二进制序列:00010010101100,总长度为14位。当接收方接收到这段电文后,将按两位一段进行译码。这种编码的特点是译码简单且具有唯一性,但编码长度并不是最短的。
2. 不等长编码
在传送电文时,为了使其二进制位数尽可能地少,可以将每个字符的编码设计为不等长的,使用频度较高的字符分配一个相对比较短的编码,使用频度较低的字符分配一个比较长的编码。例如,可以为A,B,C,D四个字符分别分配0,00,1,01,并可将上述电文用二进制序列:000011010发送,其长度只有9个二进制位,但随之带来了一个问题,接收方接到这段电文后无法进行译码,因为无法断定前面4个0是4个A,1个B、2个A,还是2个B,即译码不唯一,因此这种编码方法不可使用。
因此,为了设计长短不等的编码,以便减少电文的总长,还必须考虑编码的唯一性,即在建立不等长编码时必须使任何一个字符的编码都不是另一个字符的前缀,这宗编码称为前缀编码(prefix code)
(1)利用字符集中每个字符的使用频率作为权值构造一个哈夫曼树;
(2)从根结点开始,为到每个叶子结点路径上的左分支赋予0,右分支赋予1,并从根到叶子方向形成该叶子结点的编码
例题:
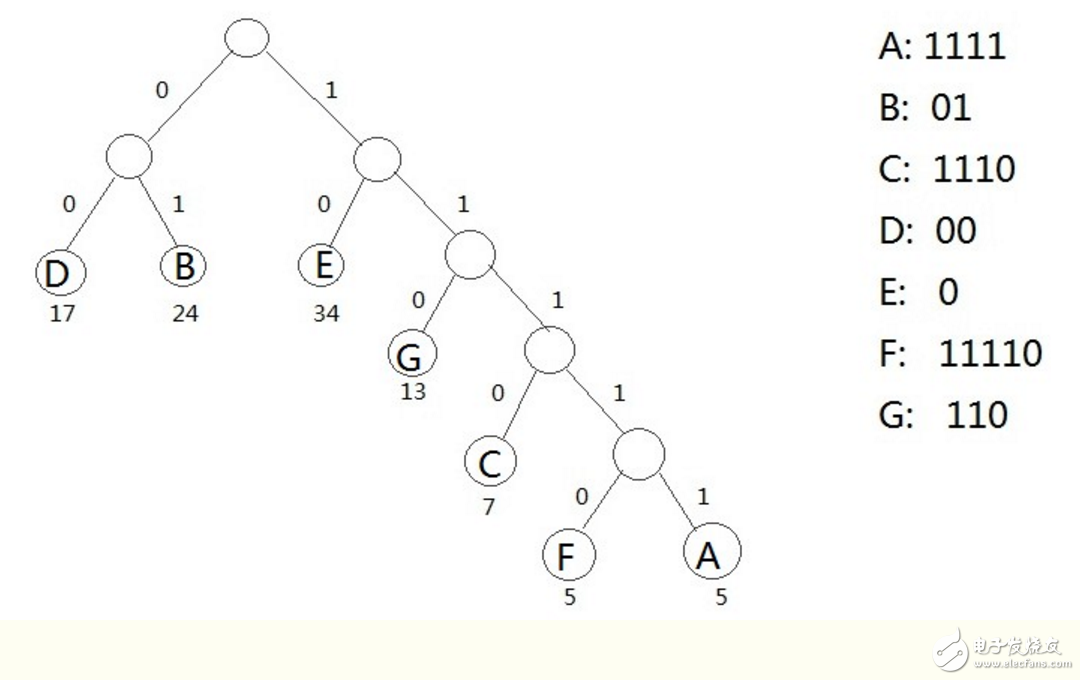
假设一个文本文件TFile中只包含7个字符{A,B,C,D,E,F,G},这7个字符在文本中出现的次数为{5,24,7,17,34,5,13}
利用哈夫曼树可以为文件TFile构造出符合前缀编码要求的不等长编码
具体做法:
1. 将TFile中7个字符都作为叶子结点,每个字符出现次数作为该叶子结点的权值
2. 规定哈夫曼树中所有左分支表示字符0,所有右分支表示字符1,将依次从根结点到每个叶子结点所经过的分支的二进制位的序列作为该
结点对应的字符编码
3. 由于从根结点到任何一个叶子结点都不可能经过其他叶子,这种编码一定是前缀编码,哈夫曼树的带权路径长度正好是文件TFile编码的总长度
通过哈夫曼树来构造的编码称为哈弗曼编码(huffman code)
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/97173.html