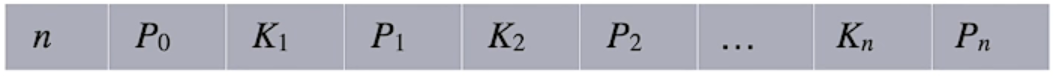二叉搜索树和二叉判定树一样吗_二叉搜索树和二叉判定树一样吗对吗

《数据结构》复习11 B树
　　一、B 树简介

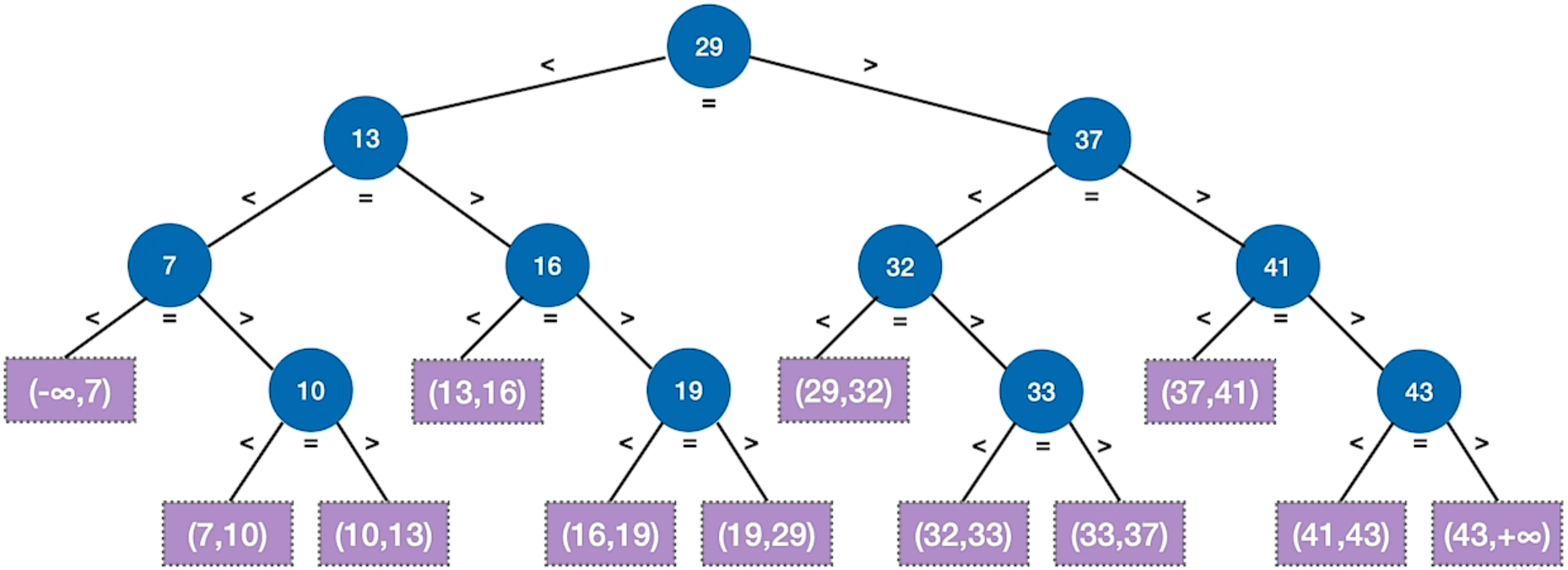
　　1.1 回顾：二叉排序树 (BST)

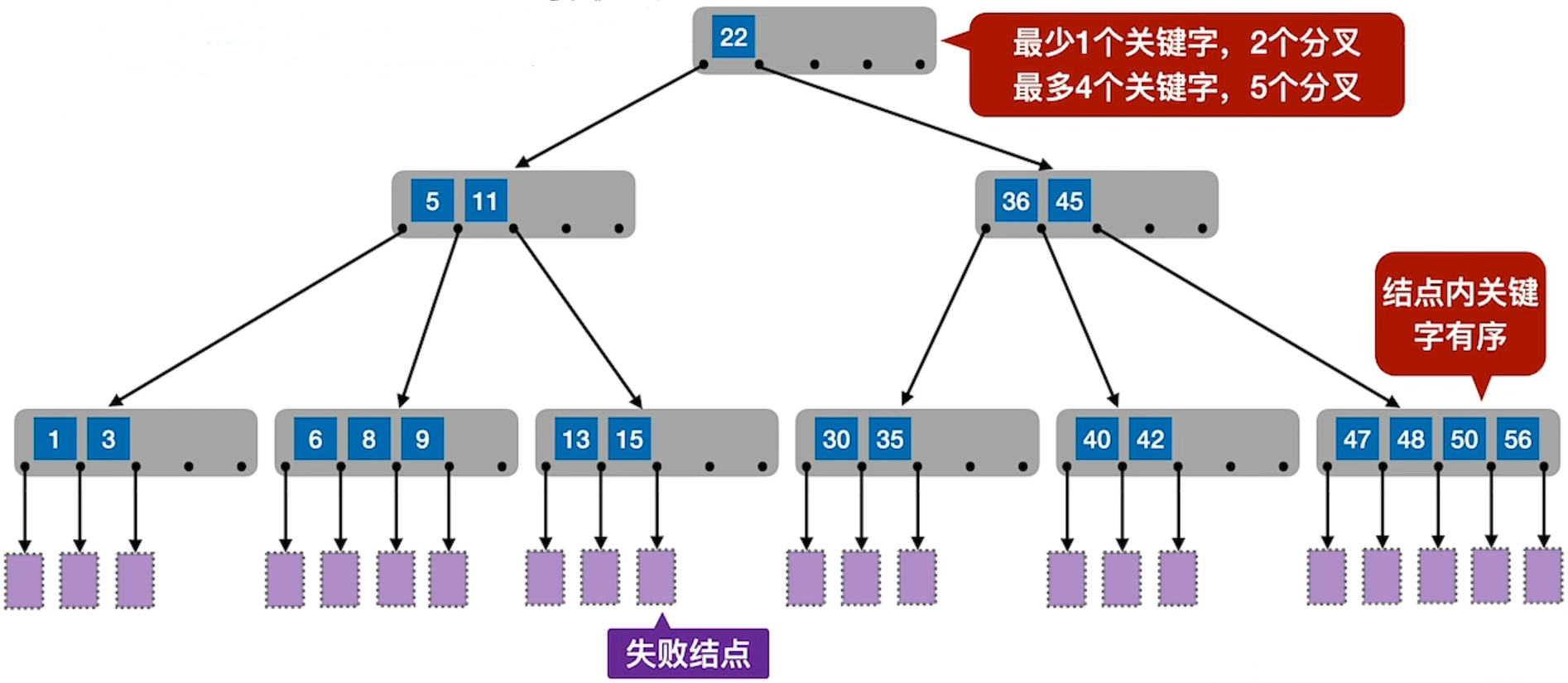
　　1.2 5叉查找树

　　1、图示

　　2、代码

　　1.3 保证查找效率

　　1、原因

　　若每个结点内关键字太少，导致树变高，要查更多层结点，效率低

　　2、策略

　　(1) m 叉查找树中，规定除了根节点外，任何结点至少有 [m/2]（m/2向上取整）个分叉，即至少含有 [m/2] – 1 个关键字

　　(2) m 叉查找树中，规定对于任何一个结点，其所有子树的高度都要相同

　　1.4 定义

　　B 树，又称多路平衡查找树，B 树中所有结点的孩子个数的最大值称为 B 树的阶，通常用 m 表示。一棵 m 阶 B 树或为空树，或为满足如下特性的 m 叉树：

　　(1) 树中每个结点至多有 m 棵子树，即至多含有 m – 1 个关键字

　　(2) 若根结点不是终端结点，则至少有两棵子树

　　(3) 除根结点外的所有非叶结点至少有 [m/2] 棵子树，即至少含有 [m/2] – 1 个关键字

　　(4) 所有非叶结点的结构如下：

　　其中，Ki ( i = 1, … ,n) 为结点的关键字，且满足 K1 < K2 < … < Kn；Pi ( i = 0, 1, …. , n) 为指向子树根结点的指针，且指针 Pi-1 所指子树中所有结点的关键字均小于 Ki，Pi 所指子树中所有结点的关键字均大于 Ki，n ([m/2] – 1 ≤ n ≤ m – 1) 为结点中关键字的个数。

　　(5) 所有的叶结点都出现在同一层次上，并且不带信息（可以视为外部结点或类似于折半查找判定树的查找失

　　败结点，实际上这些结点不存在，指向这些结点的指针为空）

　　1.5 B 树的高度

　　1、B 树的高度不包括叶子节点（失败结点）

　　2、问题：含 n 个关键字的 m 阶 B 树，最小高度、最大高度是多少?

　　最小高度：让每个结点尽可能的满，有 m – 1 个关键字，m 个分叉，则有

　　 $n\leq(m-1)(1+m^2+...+m^{h-1})=m^h-1$ ，因此 $h\geq log_m(n+1)$

　　最大高度：让各层的分叉尽可能的少，即根节点只有 2 个分叉其他结点只有 [m/2] 个分叉。

　　各层结点至少有：第一层 1、第二层 2、第三层 2[m/2] … 第 h 层 $2([m/2])^{h-2}$

　　第 h + 1 层共有叶子结点（失败结点） $2([m/2])^{h-1}$ 个

　　n 个关键字的 B 树必有 n + 1 个叶子结点（和二叉排序树类似，n 个关键字将数域切分为 n + 1 个区间），则 $n + 1 ≥ 2([m/2])^{h-1}$ ，即 $h\leq log_{[m/2]}\frac{n+1}{2}+1$

　　二、B树的插入和删除

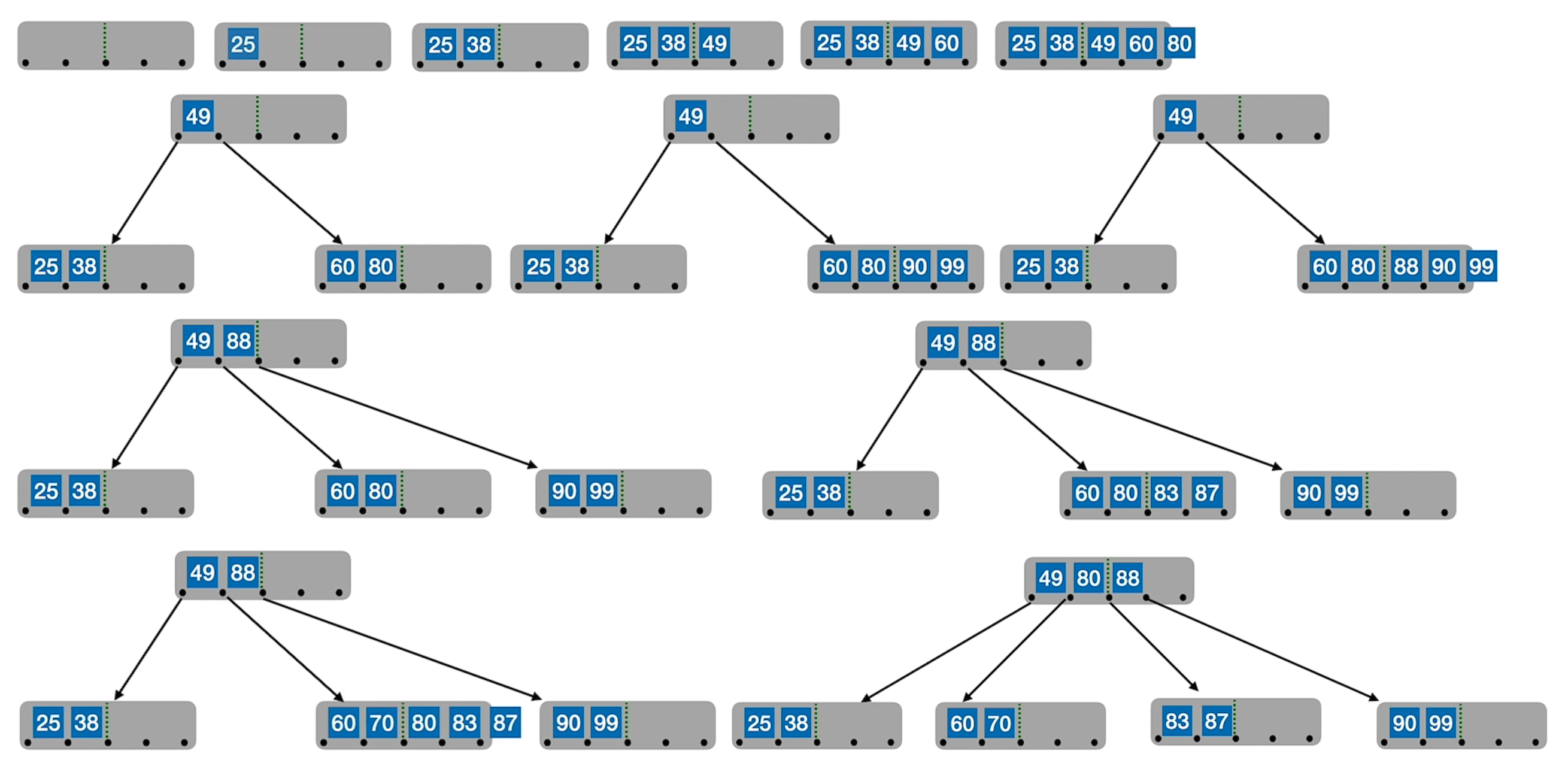
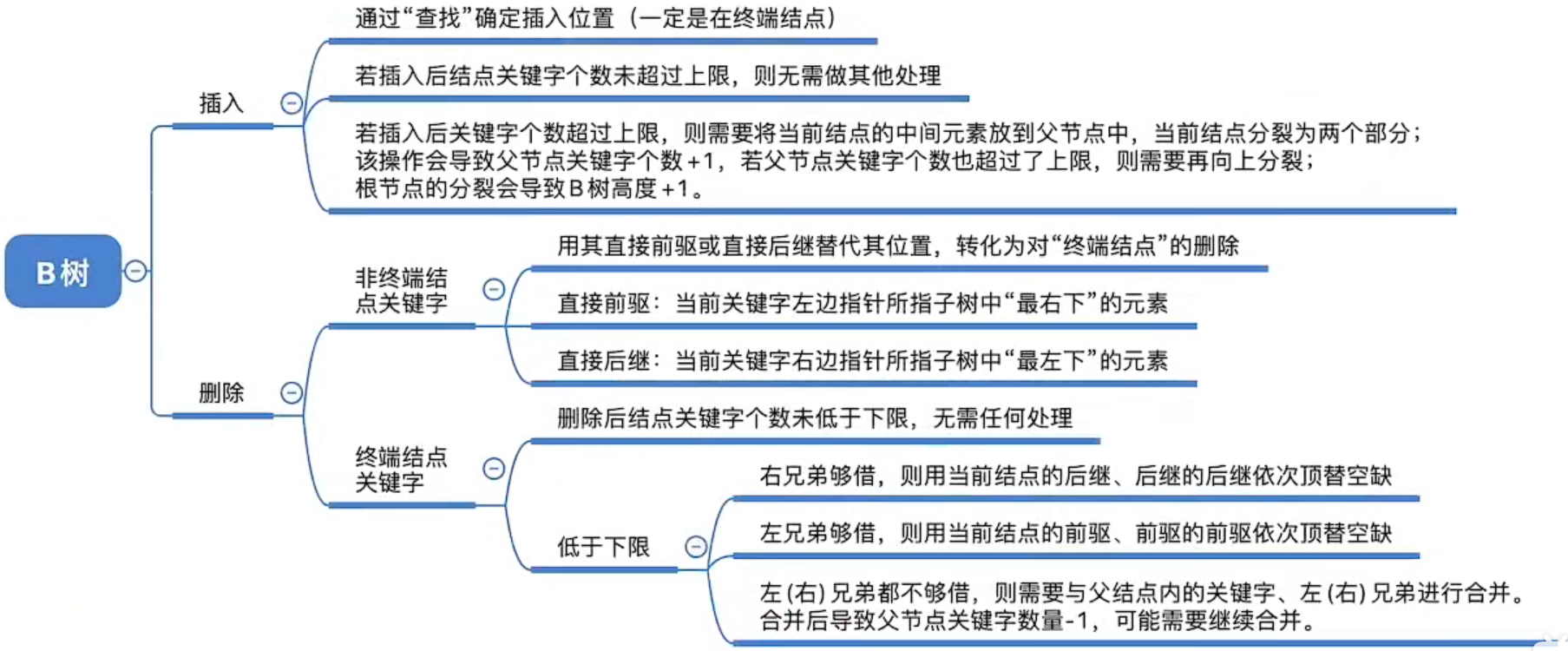
　　2.1 插入流程

　　(1) 在插入 key 后，结导致原结点关键字数超过上限，则从中间位置 ([m/2]) 将其中的关键字分为两部分，左部分包含的关键字放在原结点中，右部分包含的关键字放到新结点中，中间位置 ([m/2]) 的结点插入原结点的父结点。

　　(2) 新元素一定是插入到最底层“终端节点”，用“查找”来确定插入位置

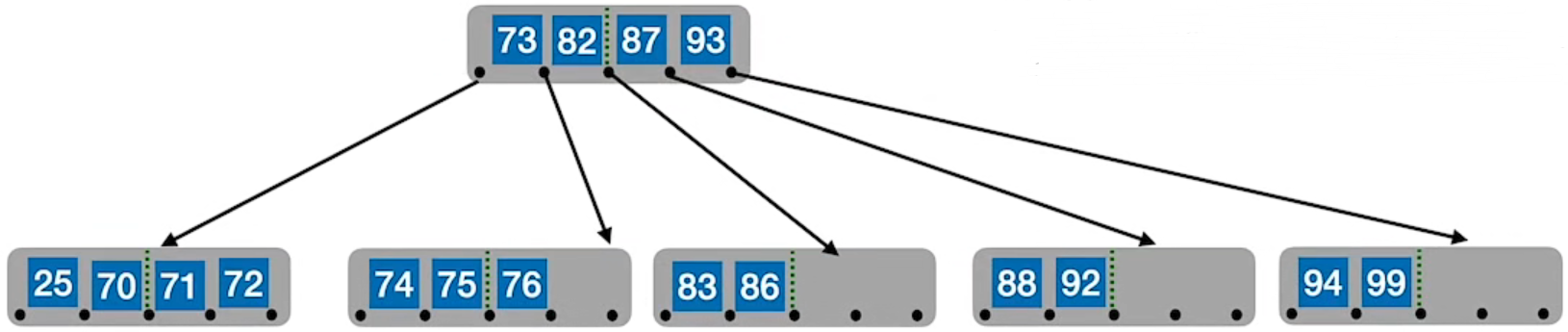
　　(3) 5 阶 B 树 —— 结点关键字个数 [m/2] – 1 ≤ n ≤ m – 1

　　即：2 ≤ n ≤ 4（注：此处省略失败结点）

　　(4) 在插入 key 后，结导致原结点关键字数超过上限，则从中间位置 ([m/2]) 将其中的关键字分为两部分，左部分包含的关键字放在原结点中，右部分包含的关键字放到新结点中，中间位置 ([m/2]) 的结点插入原结点的父结点。若此时导致其父结点的关键字个数也超过了，上限，则继续进行这种分裂操作，直至这个过程传到根结点为止，进而导致 B 树高度增 1。

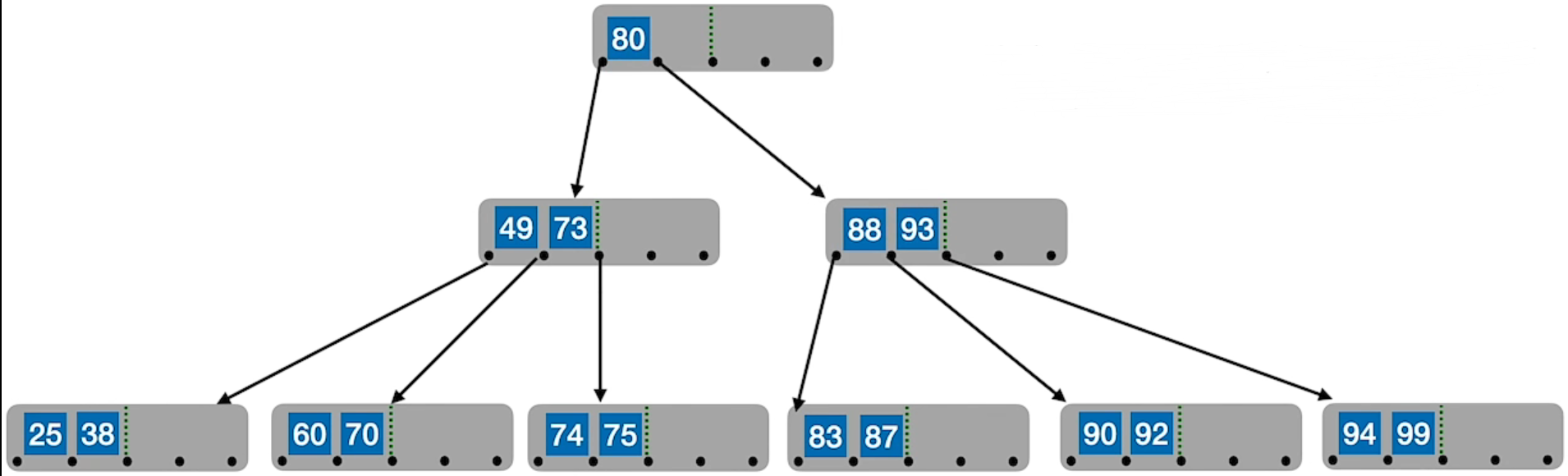
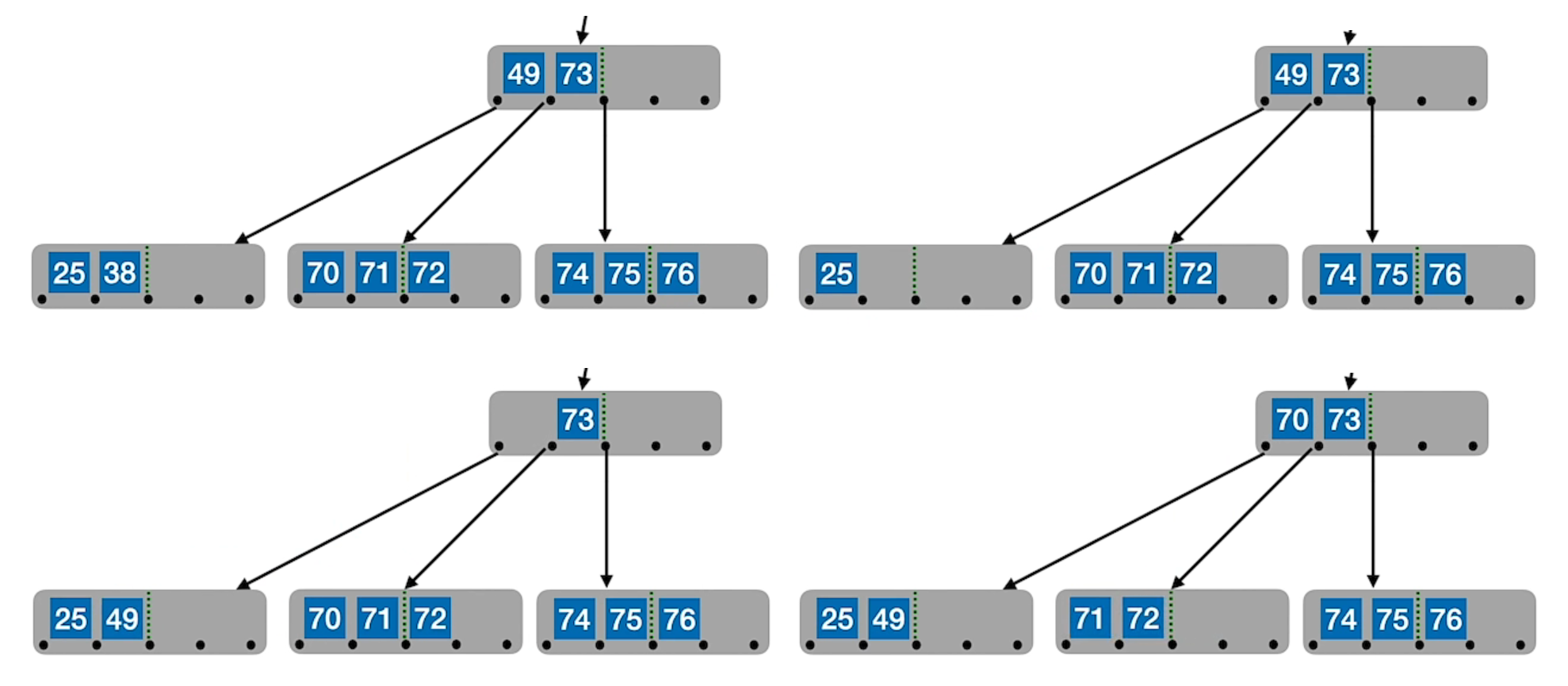
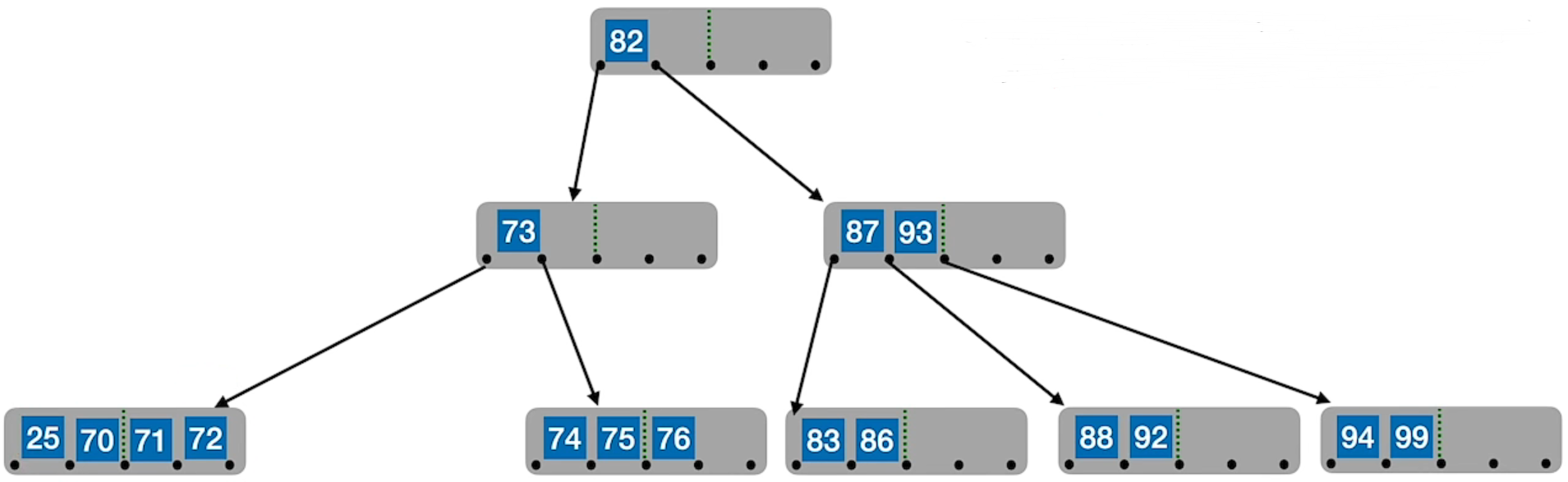
　　2.2 删除流程

　　1、若被删除关键字在终端节点，则直接删除该关键字（要注意节点关键字个数是否低于下限 [m/2] – 1）

　　2、若被删除关键字在非终端节点，则用直接前驱或直接后继来替代被删除的关键字

　　直接前驱：当前关键字左侧指针所指子树中“最右下”的元素

　　直接后继：当前关键字右侧指针所指子树中“最左下”的元素

　　对非终端结点关键字的删除，必然可以转化为对终端结点的删除操作

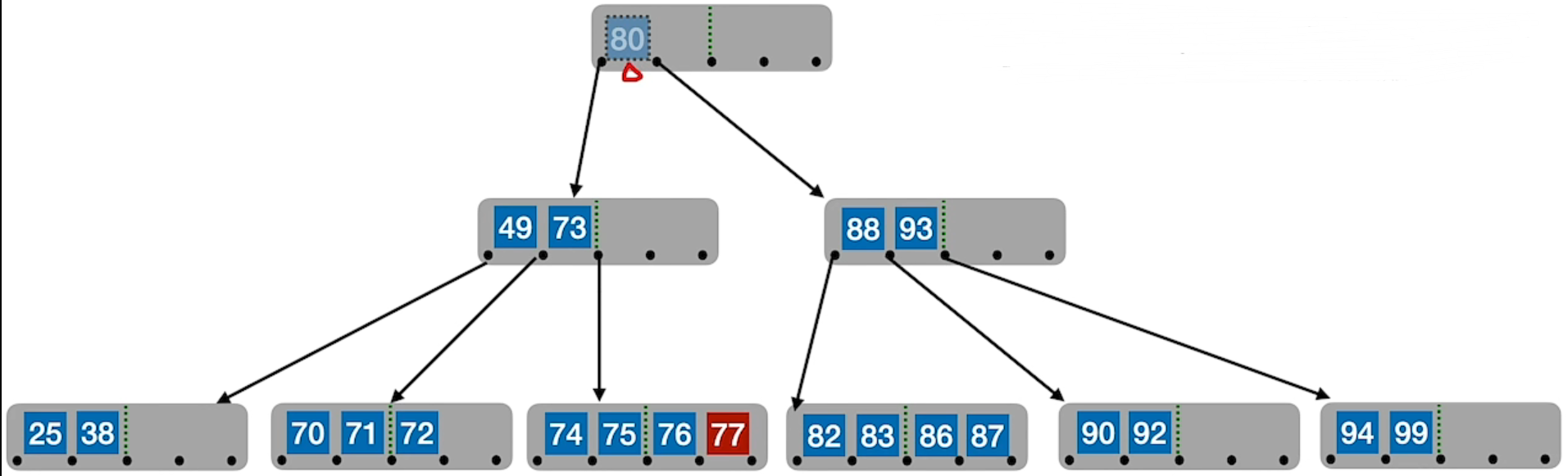
　　兄弟够借。若被删除关键字所在结点删除前的关键字个数低于下限，且与此结点右（或左）兄弟结点的关键字个数还很宽裕，则需要调整该结点、右（或左）兄弟结点及其双亲结点（父子换位法）

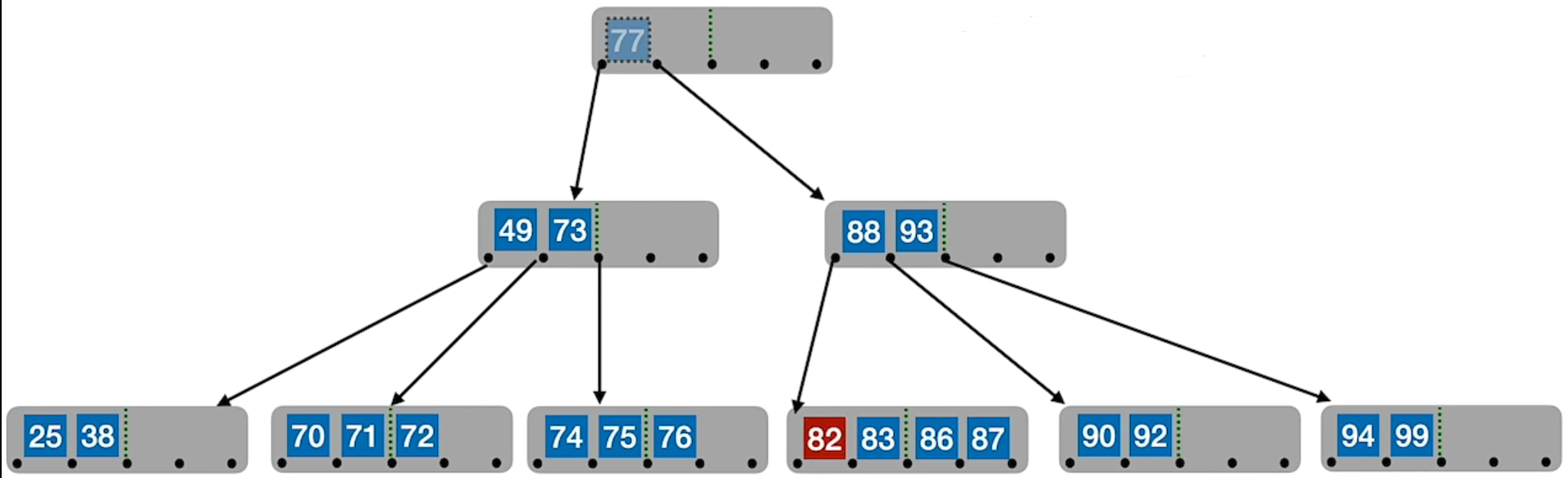
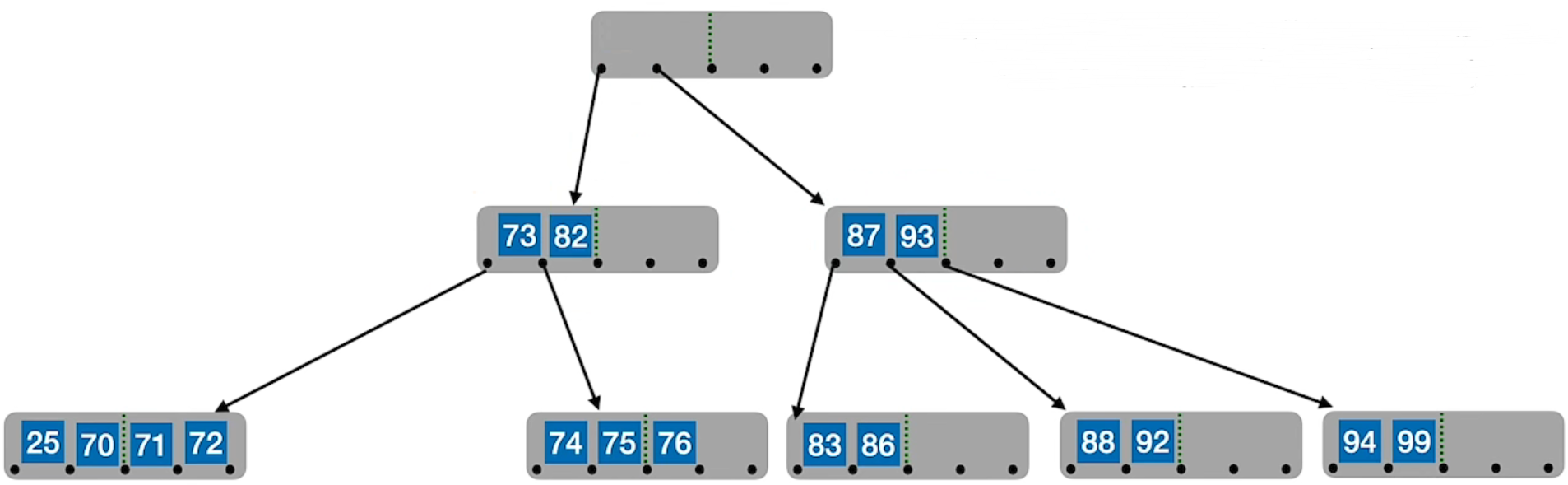
　　兄弟不够借。若被删除关键字所在结点删除前的关键字个数低于下限，且此时与该结点相邻的左、右兄弟结点的关键字个数均 = [m/2] – 1，则将关键字删除后与左（或右）兄弟结点及双亲结点中的关键字进行合并

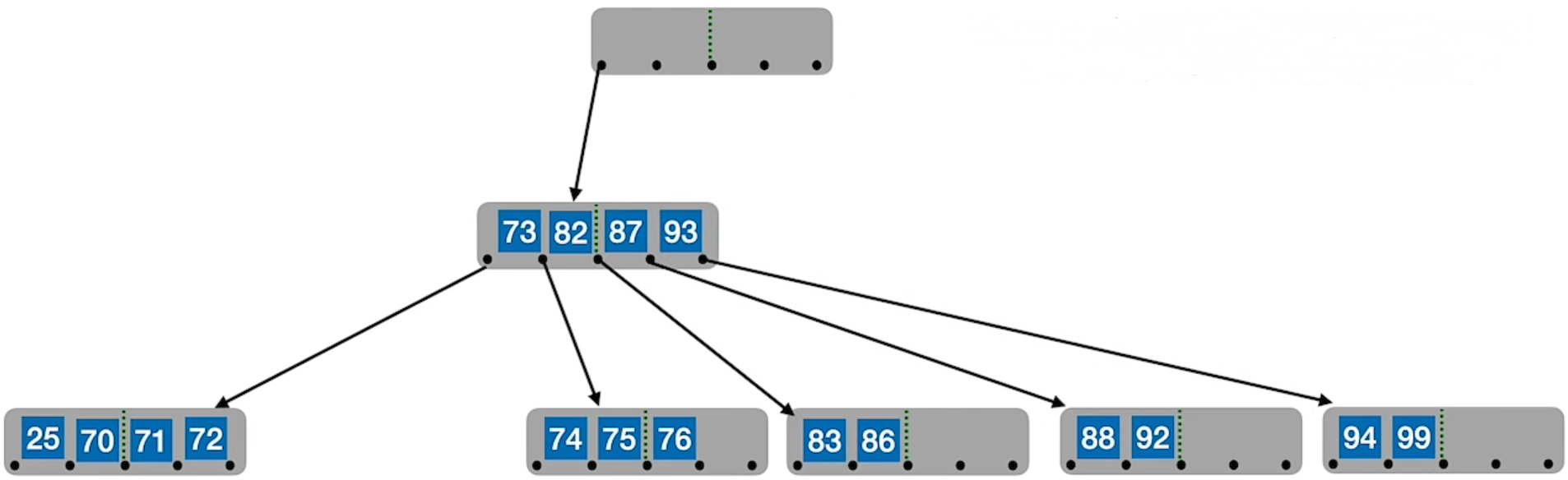
　　在合并过程中，双亲结点中的关键字个数会减 1。若其双亲结点是根结点且关键字个数减少至 0（根结点关键字个数为 1 时，有 2 棵子树），则直接将根结点删除，合并后的新结点成为根;若双亲结点不是根结点，且关键字个数减少到 [m/2] – 2，则又要与它自己的兄弟结点进行调整或合并操作，并重复上述步骤，直至符合 B 树的要求为止。

　　2.3 总结

　　三、B+树

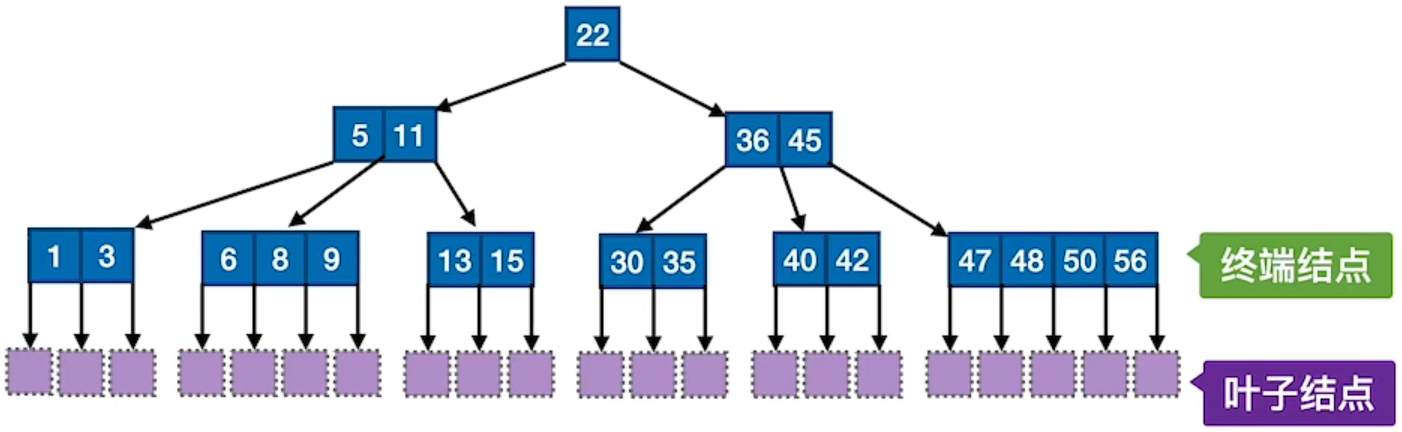
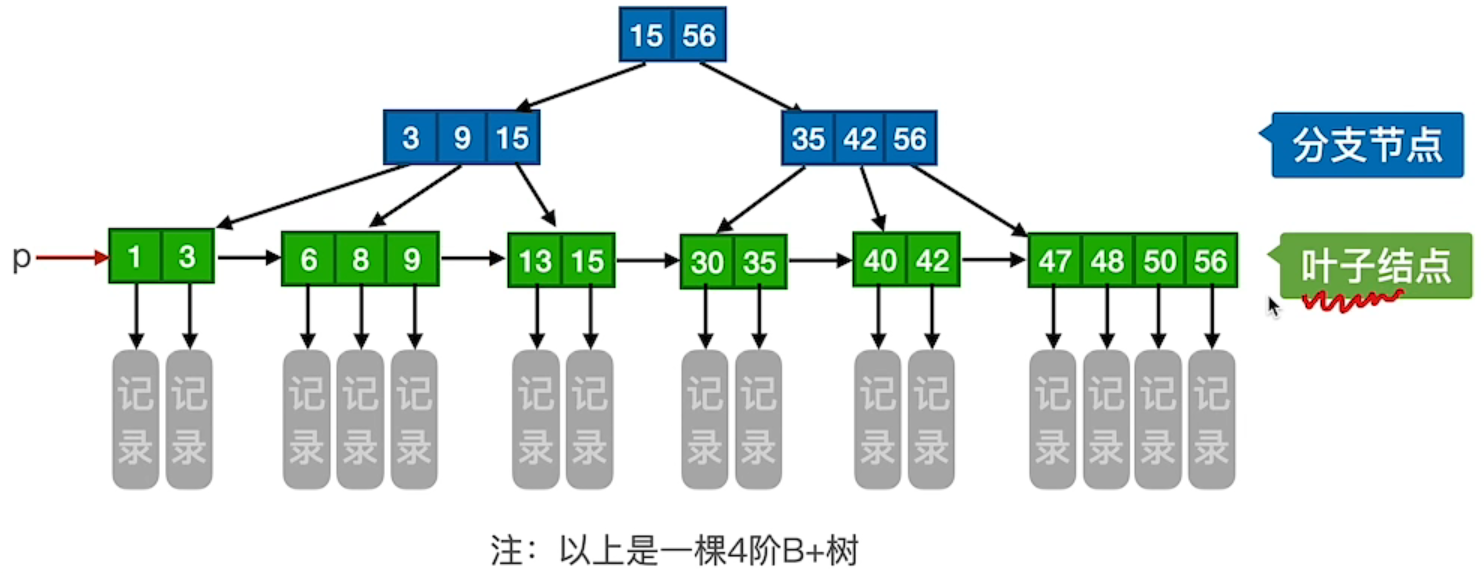
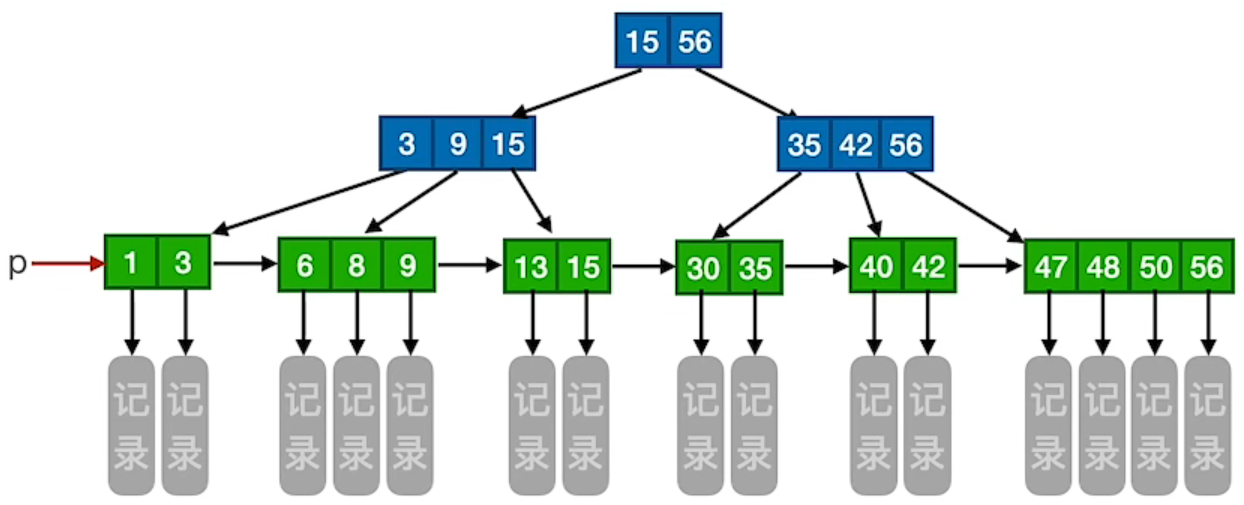
　　3.1 图示

　　3.2 定义

　　一棵 m 阶的 B+ 树需满足下列条件：

　　(1) 每个分支结点最多有 m 棵子树（孩子结点）

　　(2) 非叶根结点至少有两棵子树，其他每个分支结点至少有 [m/2] 棵子树（要追求“绝对平衡”，即所有子树高度要相同）

　　(3) 结点的子树个数与关键字个数相等（B树中关键字比子树少一个）

　　(4) 所有叶结点包含全部关键字及指向相应记录的指针，叶结点中将关键字按大小顺序排列，并且相邻叶结点按大小顺序相互链接起来（支持顺序查找）

　　(5) 所有分支结点中仅包含它的各个子结点中关键字的最大值及指向其子结点的指针

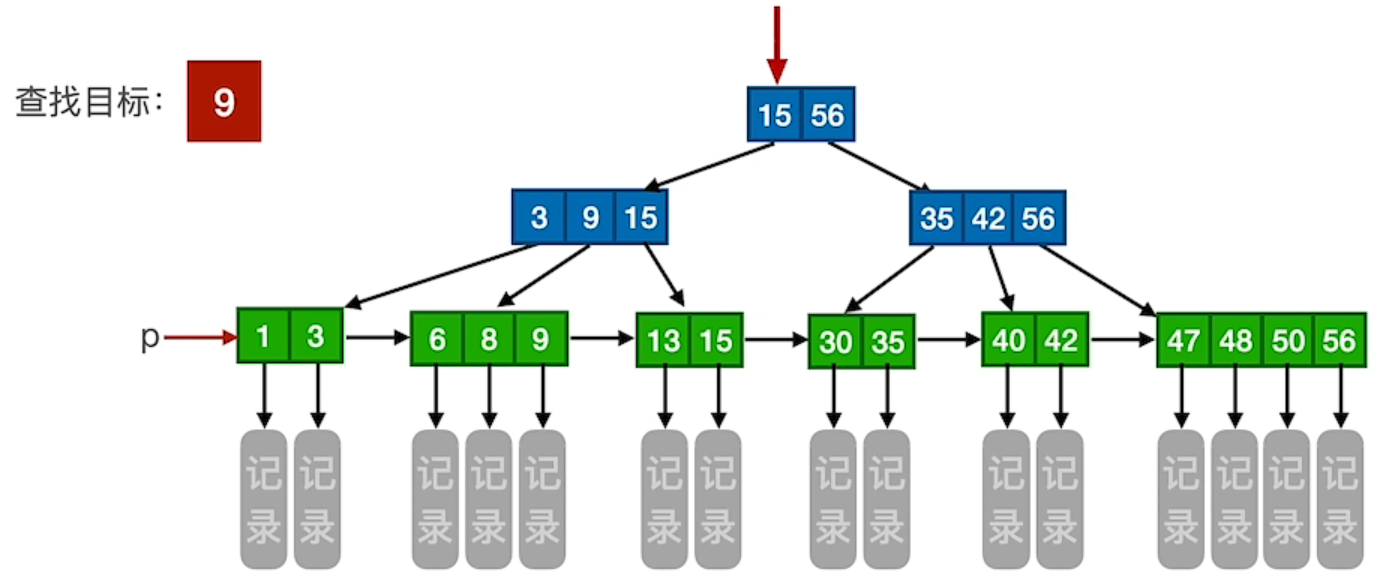
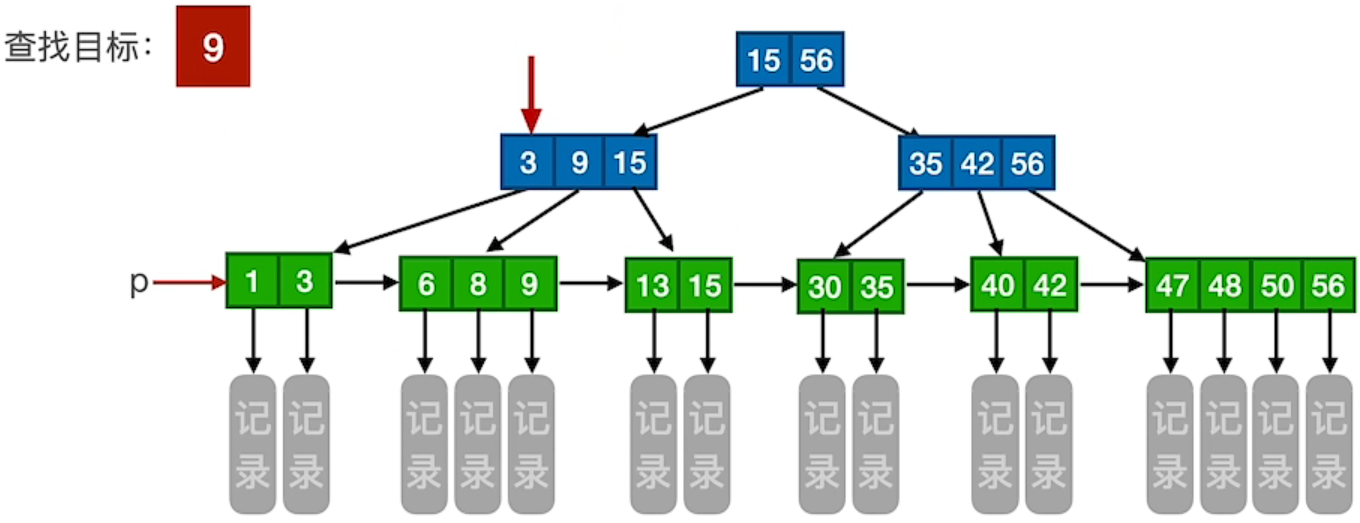
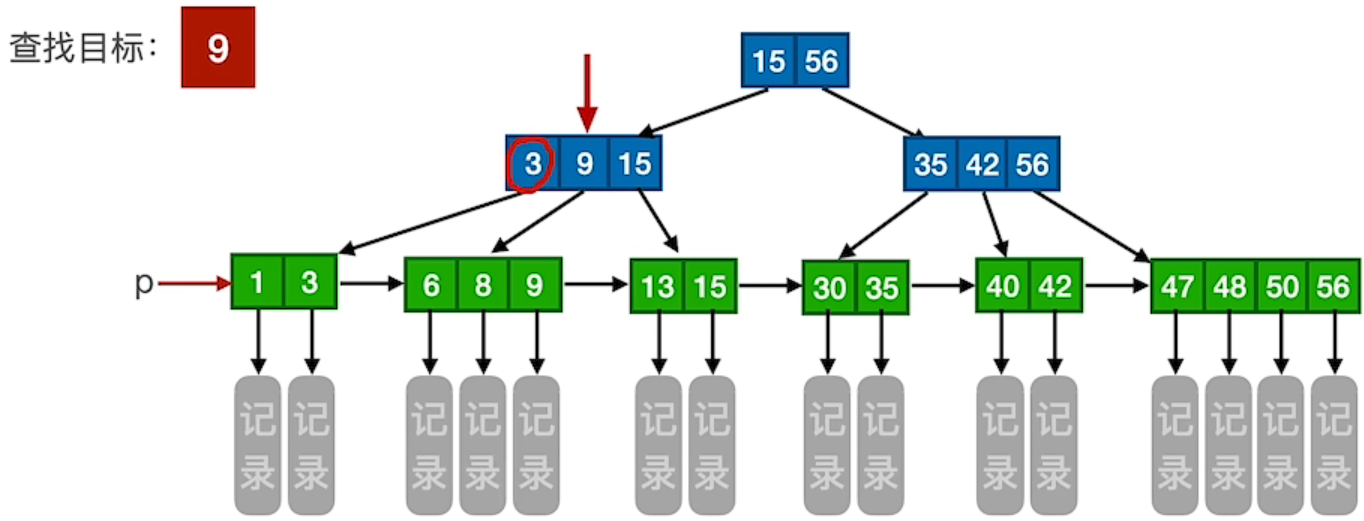
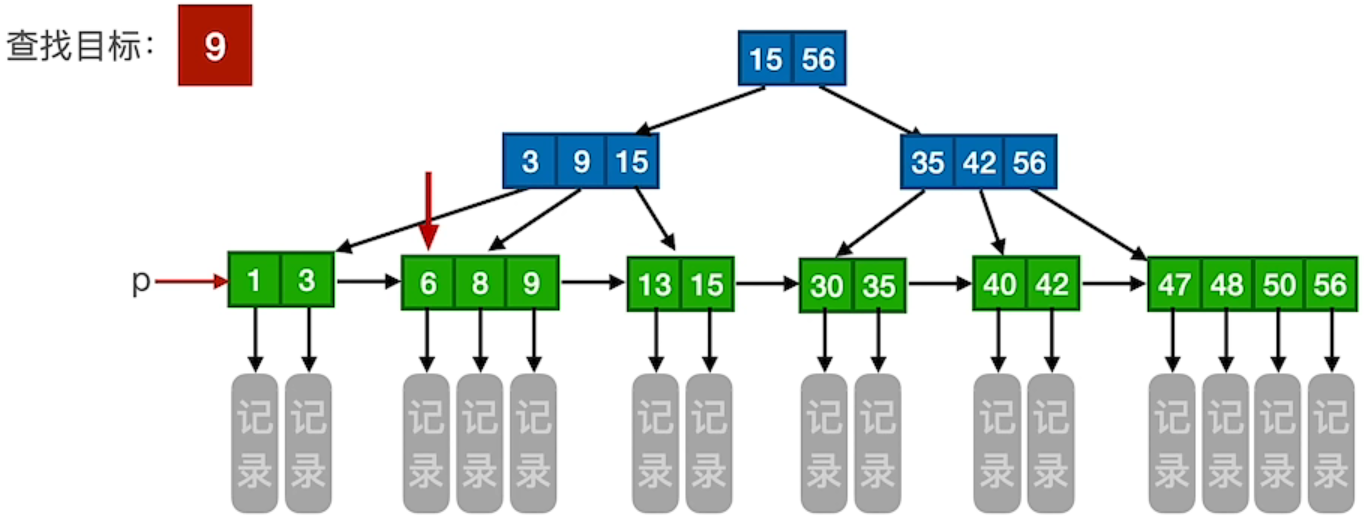
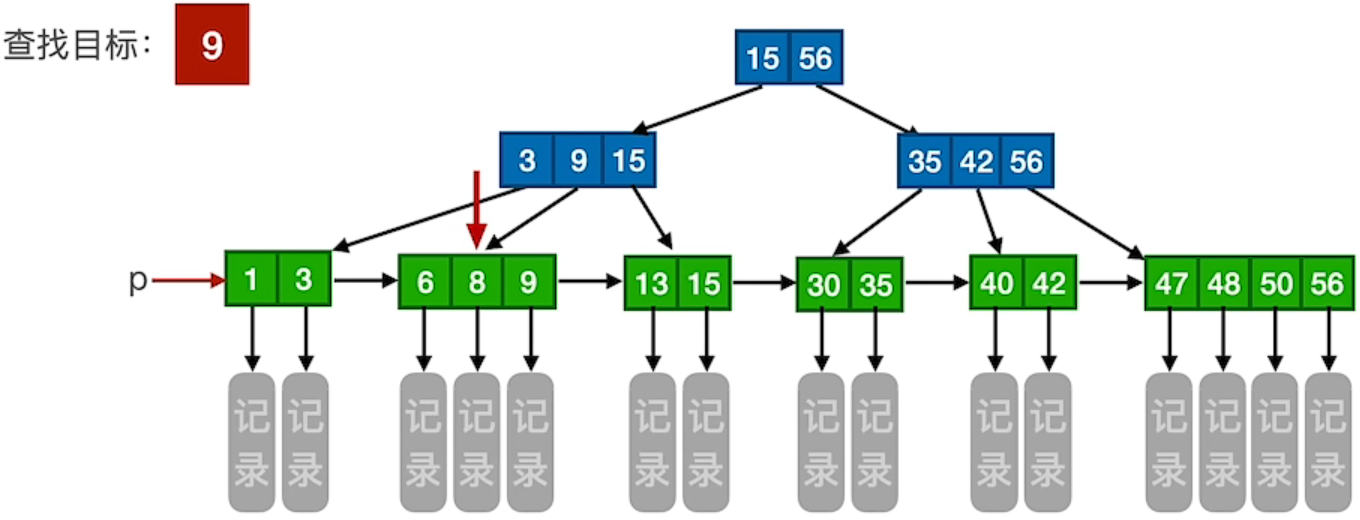
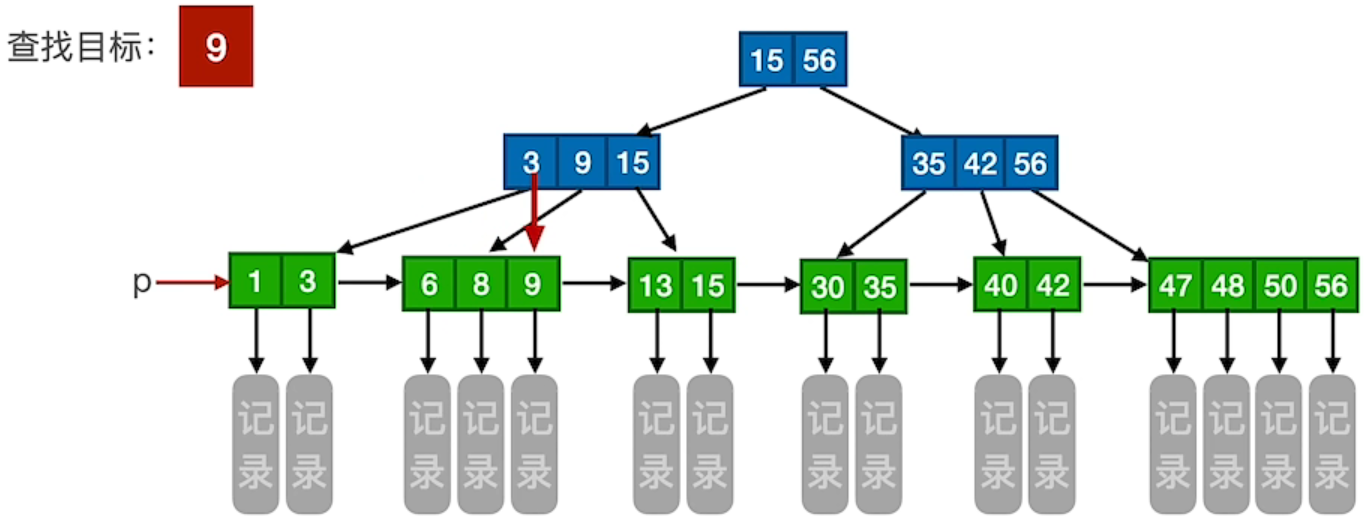
　　3.3 B+树的查找

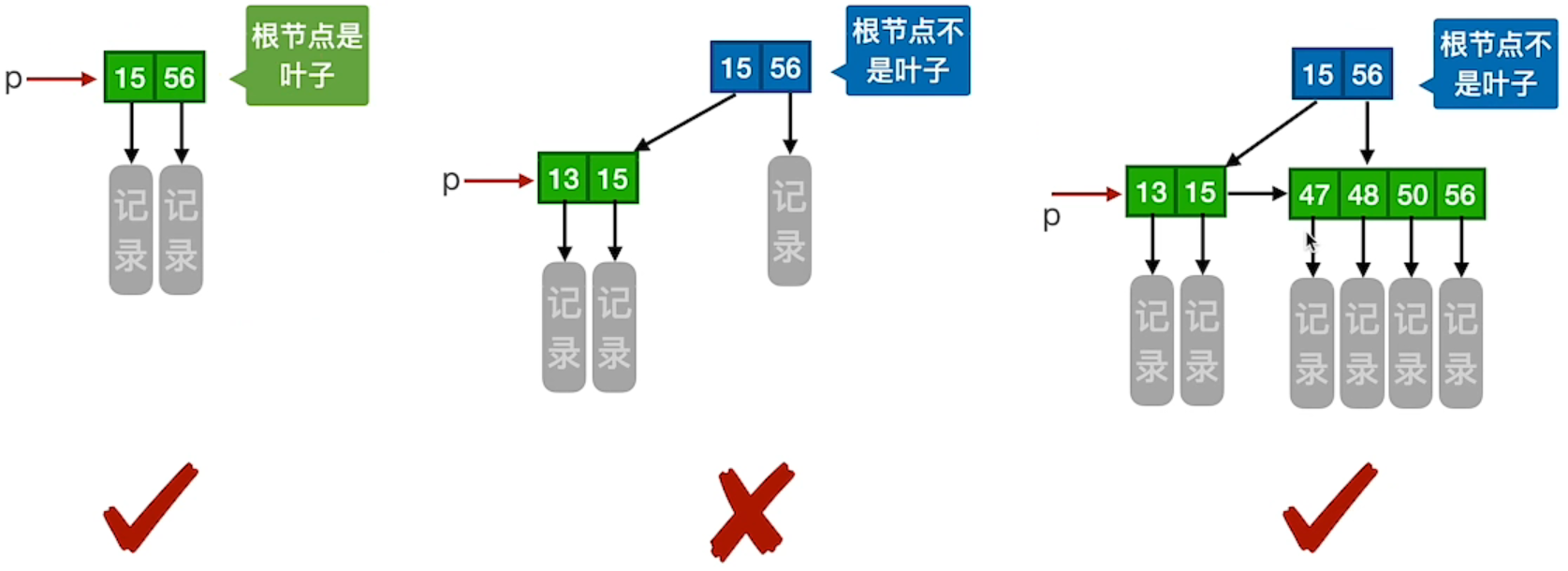
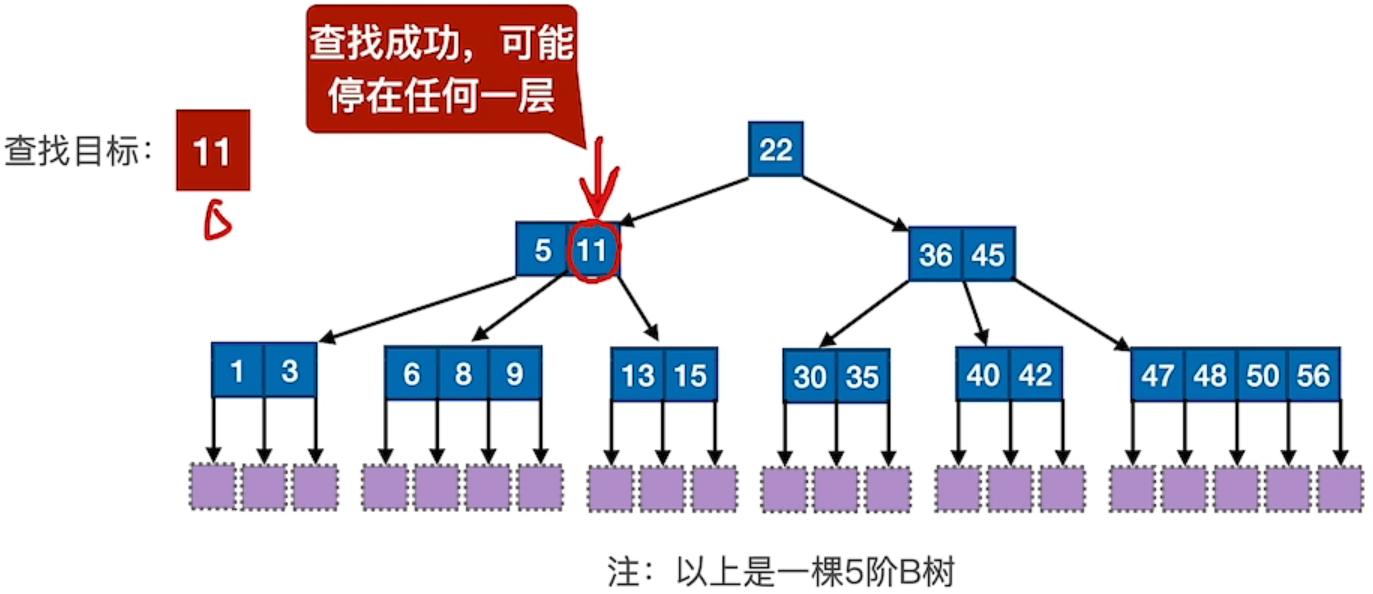
　　1、查找成功

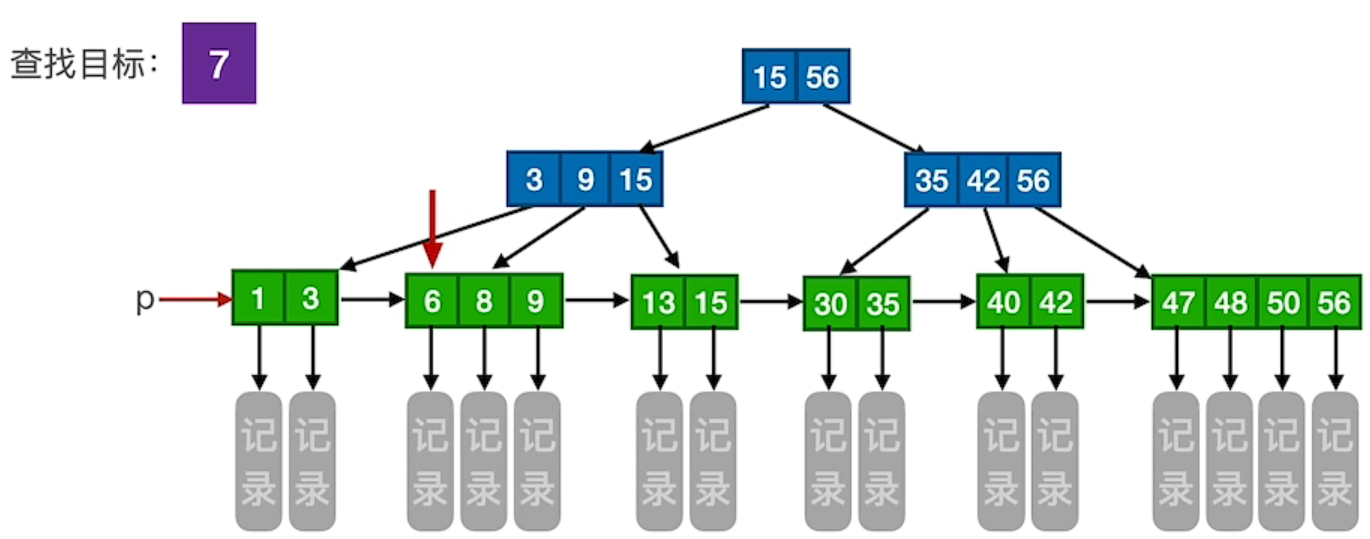
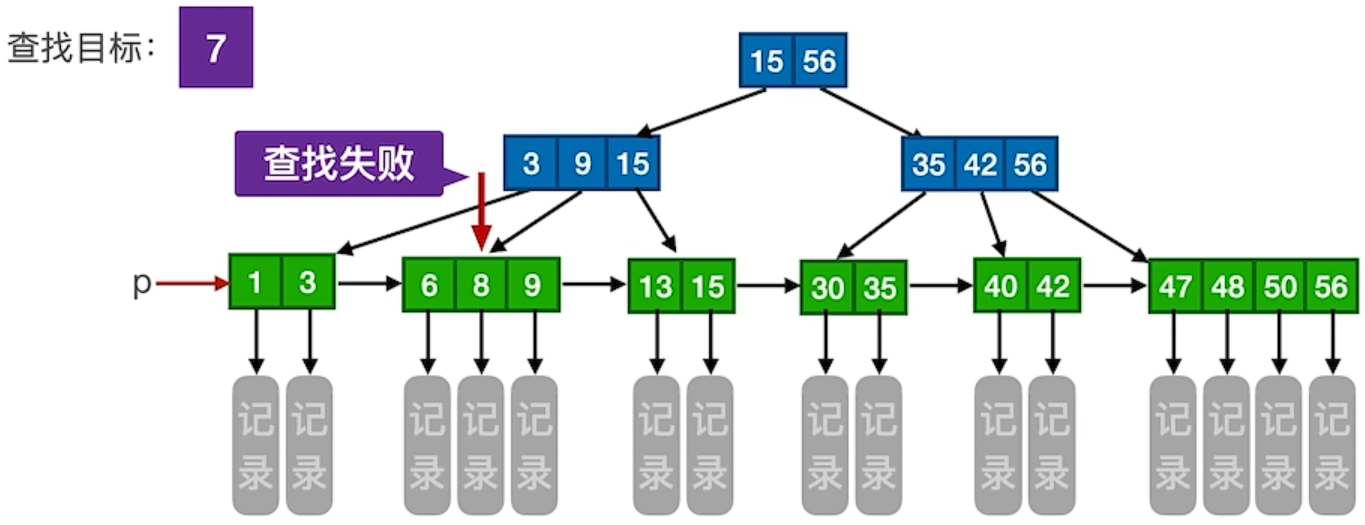
　　2、查找失败

　　3、对比 B树的查找

　　B+ 树中，无论查找成功与否，最终一定都要走到最下面一层结点

　　B 树中，查找成功，可能停在任何一层

　　3.4 B+树和 B树对比

　　1、m 阶 B+树结点中 n 个关键字对应 n 棵子树

　　m 阶 B树结点中 n 个关键字对应 n + 1 棵子树

　　2、m 阶 B+树根节点的关键字数 n ∈ [1, m]，其他结点的关键字数 n ∈ [[m/2], m]

　　m 阶 B树根节点的关键字数 n ∈ [1, m – 1]，其他结点的关键字数 n ∈ [[m/2] – 1, m – 1]

　　3、m 阶 B+树中，叶结点包含全部关键字，非叶结点中出现过的关键字也会出现在叶结点中

　　m 阶 B树中，各结点中包含的关键字是不重复的

　　4、m 阶 B+树中，叶结点包含信息，所有非叶结点仅起索引作用，非叶结点中的每个索引项只含有对应子树的最大关键字和指向该子树的指针，不含有该关键字对应记录的存储地址

　　m 阶 B树的结点中都包含了关键字对应的记录的存储地址

　　5、在 B+树中，非叶结点不含有该关键字对应记录的存储地址。

　　可以使一个磁盘块可以包含更多个关键字，使得 B+ 树的阶更大，树高更矮，读磁盘次数更少，查找更快。

　　解释：一个索引 15、56 和另外一个索引 3、9、15 和另外一个索引 35、42、56 是存在不同的磁盘块里面的。每查找一次结点的时候都要进行一次读磁盘的操作，直到找到最下面的叶子结点，每次读取磁盘块都是一次慢速操作，所以要让树尽可能矮。一个磁盘块只有 1KB 大小，所以要让一个磁盘块尽可能包含索引信息，所以 B+树非叶子结点只包含索引和地址，不包含记录。

　　技术应用：关系型数据库的“索引”（如MySQL）

　　3.5 总结

　　参考文献：

　　【1】视频：王道计算机考研数据结构

二叉搜索树和二叉判定树一样吗_二叉搜索树和二叉判定树一样吗对吗

相关推荐