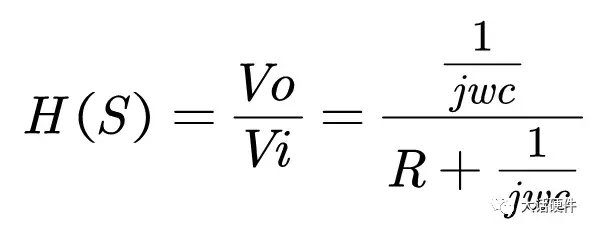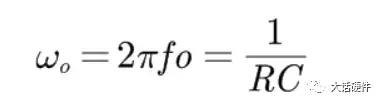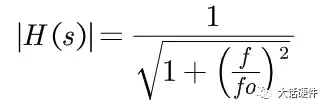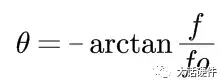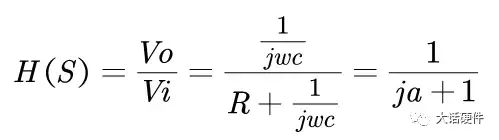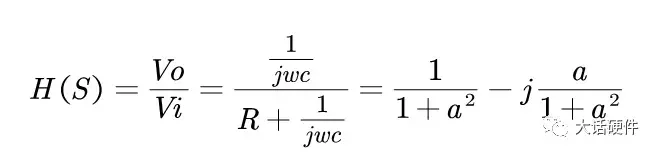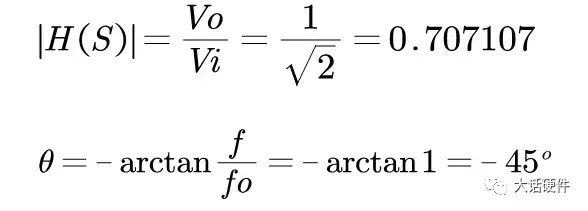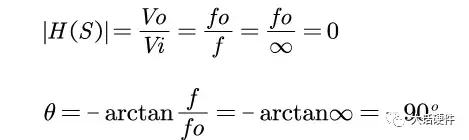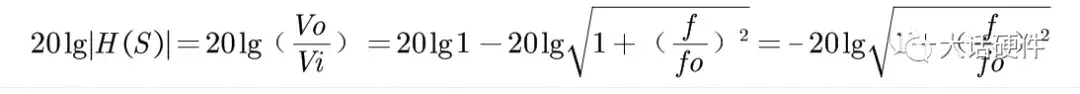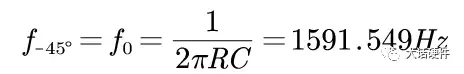详细推导波特图增益和相位曲线
最近因为项目需求,在回看波特图方面的内容。大三那会,《自动控制原理》这本书里面就讲过这些东西,但是那时候总感觉学这些没啥用,反正以后也用不到,对这种课程的重视度不是很高。
工作后发现,只要你从事的是和本专业相关的工作,大学学过的很多理论课程在后面大概率都会用到。曾经那些我们在学校以为用不上的东西,熟不知在后面用处还多着呢。所以啊,仅仅只是我们的以为而已!
现在还在学校的同学,对待《自动控制理论》、《信号与系统》、《通信原理》这样的核心专业课,建议还是好好学习一下,认真听听课。哪怕是考试完以后就会忘掉,但当我们再次捡起书本时,或多或少还是会些模糊的记忆存在。相比完全没怎么听过课的人来说,学起来也会更快。今天这篇文章想把近段时间关于波特图方面学习的内容整理一下。波特图将会是梳理闭环控制这个系列的开始。目前的计划是,以无源器件为基础,然后结合运放,再过渡到开关电源的环路控制方面。如果对这方面感兴趣的朋友,可以持续一起学习起来,目标就是掌握开关电源的闭环控制。1. 什么是波特图?
波特图最常见的应用是在线性非时变的系统中,用于对传递函数的增益和相位进行分析,从而判断出系统随频率的响应是否稳定。因此,波特图又称为幅频响应和相频响应曲线图。
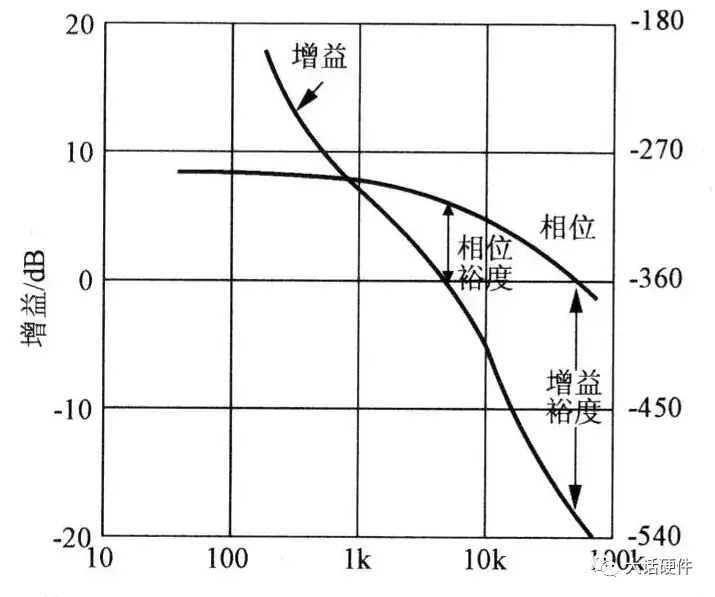
下面就是在电路分析中最常见的波特图。
图1. 波特图示例
2. 理想器件和真实器件有什么区别?
理想的电阻如下图所示
图2. 理想的电阻
理想的电阻,无论输入什么样的信号,在增益和相位上,不会有变化(忽略电阻产生的压降)。毕竟只要有电流流过电阻,输出端相比输入端的电压肯定会有略微降低。因此,使用波特图研究理想电阻对输入信号的响应,没什么意义。
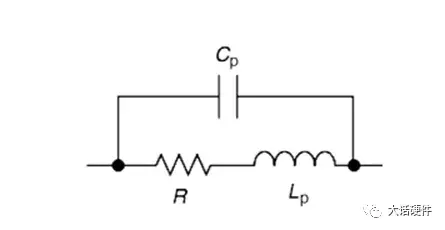
而在真实的世界中,电阻由于生产工艺制造,PCB板上走线,SMT焊接等一系列的操作,理想的电阻,并不是我们想象中的那样。只要把电阻用在电路中,它就会自带寄生电感和寄生电容,实际的等效模型如下所示:
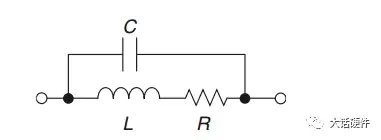
图3. 实际的电阻模型
我们知道,电容和电感的阻抗会随着频率的改变而改变。那么实际的电阻也会信号频率的改变产生响应。
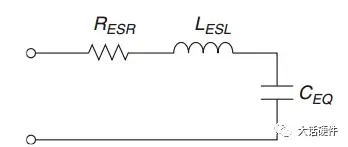
实际的电容模型如下:
图4. 实际的电容模型
实际的电感模型如下:
图5. 实际的电感模型
理想电阻对不同输入信号的频率没有响应,无论在什么条件下,它一直表现出来同样的阻抗,在全频率范围内,阻抗一直会保持同样的阻值。但是结合电容和电感的等效模型可知,实际的电阻并不会一直保持同样的阻抗。
综上可知,真实的物理世界中,无论是独立的电阻,独立的电容,独立的电感,都会对输入信号的频率有响应。不同频率的信号通过这三者组成的电路,所得到输出信号幅度和相位会有区别。
从上面的分析可以看出,现实世界中的电子元器件,电阻,电容,电感都会对输入信号频率的改变产生响应,而半导体器件由于CMOS工艺的原因,会在半导体管极间产生寄生电容,加工制造的PCB走线,会有寄生电感的存在。
所以,加工制造完毕的、实际的PCBA单板,输出信号都是会受到输入信号因频率改变而带来的的影响。既然是这样,那么波特图就能很好的帮助我们分析电路对信号频率改变的响应了。
3. 滤波器和波特图
滤波器的作用是对不同频率输入信号,实现不同的增益和相移,以形成输出。
对设计滤波器的人来说,比较的是在特定的频率内,到底有怎样的增益和相移。根据前面分析的内容,波特图刚好是研究增益和相移。所以要想设计一个满足性能的滤波器,必须要学会波特图。下面以一个低通滤波器为例,讲述如何分析和使用波特图。
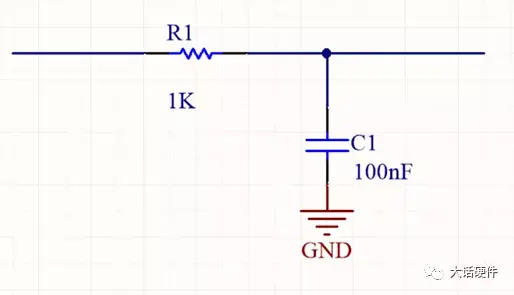
图6. RC低通滤波电路
输入信号为VI,输出信号为Vo,根据电阻分压的原理,可以计算出RC低通滤波的传递函数为:
图7. RC电路传递函数
从传递函数可以看出,传递函数受到输入信号频率ω的影响。要知道Vo信号经过RC后的变化,就需要了解H(s)的特性,为了便于分析,令
图8. RC时间常数其中,RC为电路的时间常数。
根据复数性质,计算出H(s)的幅值和相位大小分别为:
图9. RC电路幅值和相位
关于传递函数的幅值和相位计算,目前很多书上都是直接给出答案,这里推导一下结论的来源。为了方便计算,可以令传递函数为下面的这样的形式:
图10. 传递函数复数形式求H(S)的幅值和相位,需要对其分子分母有理化,可以计算得到:
图11. 传递函数分子分母有理化
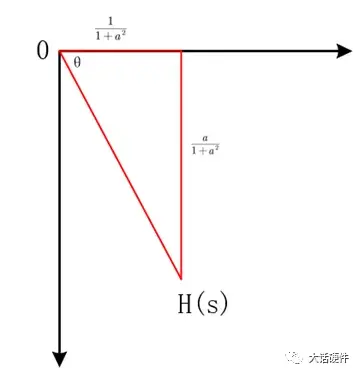
幅值和相位根据下面的坐标图,就能计算出上面幅度|H(s)|和相位θ的大小。
图12. 传递函数在复平面中
4. RC电路对频率的响应
根据|H(s)|的表达式,1和f/fo之间的关系大小,会使|H(s)|有不一样的结果。因此,1和f/fo之间的关系,将|H(s)|分为三个阶段。
(1)当 f/fo <<1 时
f远小于fo,可认为输入信号为直流信号,此时H(S)的增益和相位表达式中将f/fo这一项忽略。则增益为1,输出信号幅值等于输入信号幅值。此时相位θ也非常小,几乎为0。也就是说,在f非常小时,输出跟随输入变化,幅度不变化,相位也不变化。
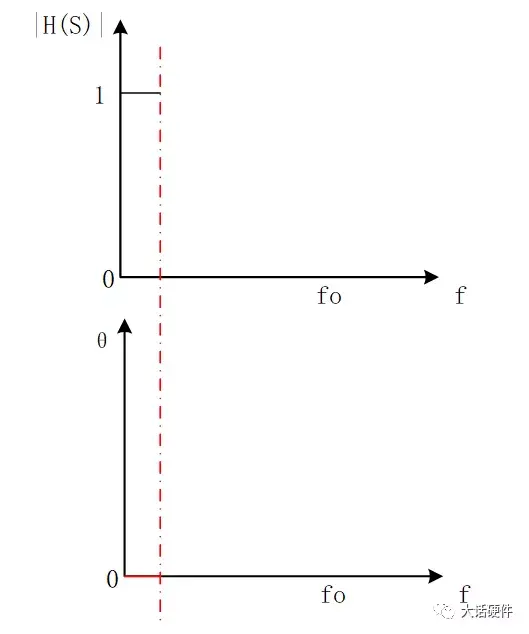
增益和相位的曲线如下图所示:
图13. 增益相位曲线
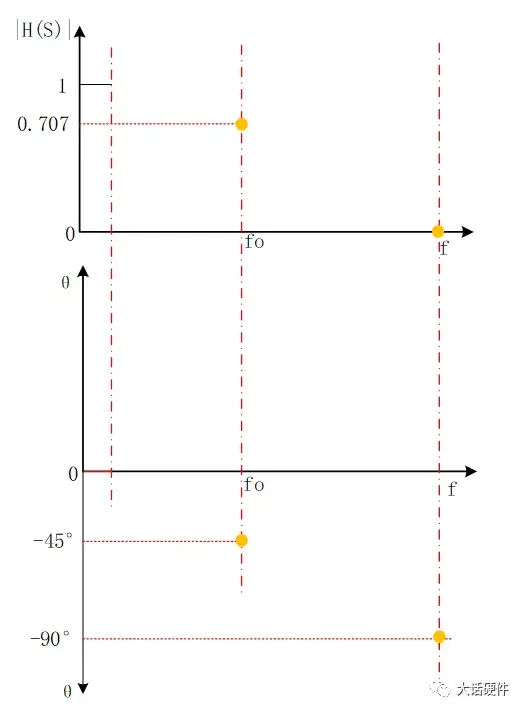
(2)当f/fo =1时
输入信号频率f刚好和RC乘积相等,此幅值和相位的大小为:
图14. 特征频率处的增益和相位
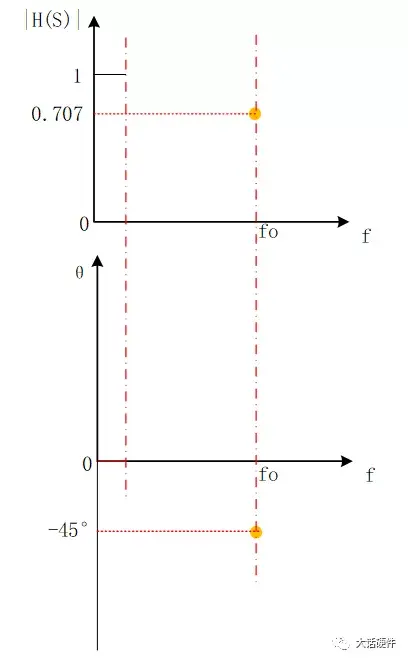
增益和相位的曲线如下图所示:
图15. 增益和相位曲线
根据上面的内容,我们只能分析出f在很小时和f=fo时的幅值和相位,画出来的增益和相位曲线如图13和图15所示,在f趋近于fo的过程中,幅值和相位是怎么样的变化的还不知道。先不着急得到变化趋势,接着把第三阶段分析完。
(3)当f/fo >>1 时
增益和相位的大小为:
图16. 无穷大频率处的增益和相位
增益和相位的曲线如下图所示:
图17. 增益和相位曲线
根据输入信号的变化和传递函数的表达式,我们推出了全频率范围内输出信号的变化。可以得到的结论是:在RC滤波电路中,输入信号的频率越高,输出信号频率越少,而且相位滞后越大。
当f非常小时,输出信号在增益和相位和输入信号保持一致。当f非常大时,此时输出端的信号几乎为0,相位滞后90°,且此时研究相位也没有意义。
5. 波特图
波特图可以研究系统的频率响应,且能描述增益和相位,而增益和电压放大倍数刚好能对应起来,所以RC电路的响应,也可以用波特图进行描述。
根据波特图的定义,XY轴坐标需要改为对数坐标,即横轴用lgf来表示,纵轴用20lg(A)来描述。将RC电路输入输出增益和相位响应曲线,幅值和频率换成对数坐标系后:
增益的表达式为:
图18. 对数增益表达式
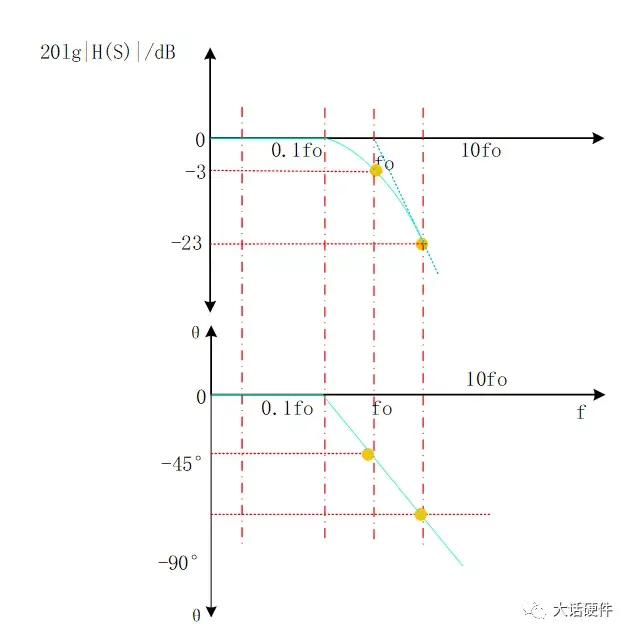
增益和相位的对数幅频特性为:
图19. 增益和相位的波特图
由H(s)的对数公式可知,只有在f>>fo 时,斜率才是-20dB/10倍的频程,在0~-3db之间,这个关系式并不成立。
在波特上,按照0.1fo的频率作为增益和相位更改的起点,代入关系式中,可以计算出增益误差为-0.04dB,相位误差为-5.71°。
可能有人会有疑问,为什增益和相位的变化要从0.1fo开始,是0.01fo不行吗?结论是,研究0.01fo没什么意义,代入到公式可以计算出,此时增益基本为0dB,相移基本为0°,所以在低频阶段,曲线一直和坐标轴保持一致。
6. TINA仿真测试
使用TI的TINA软件对RC电路进行仿真,看输出信号随着输入信号变化趋势。其中比较特殊的点为产生-45°相移频率,即输入信号频率和fo的频率相等,可以计算出
图20. 特征频率仿真波形如下:
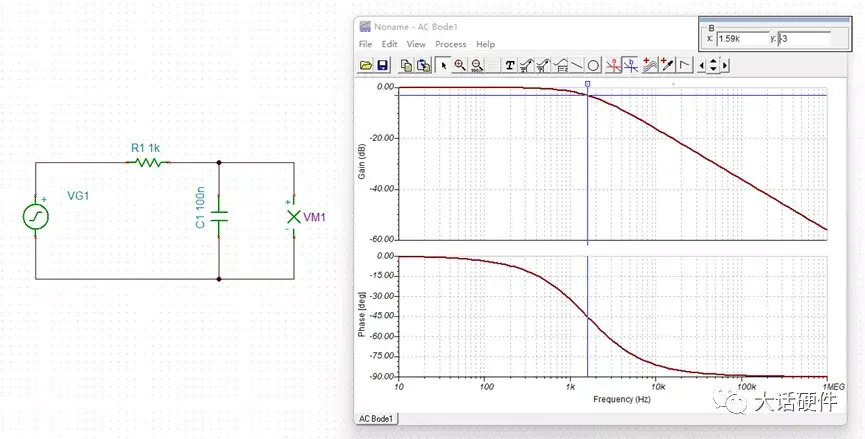
图21. 1591Hz仿真波形分析波特图,输入信号频率为1.59KHz时,输出信号相比输入信号产生了-45°的相移,此时的增益为-3dB。也就是输出信号是输入信号的0.707倍,信号被衰减了。如果输入信号频率为0.1fo,仿真波形如下:
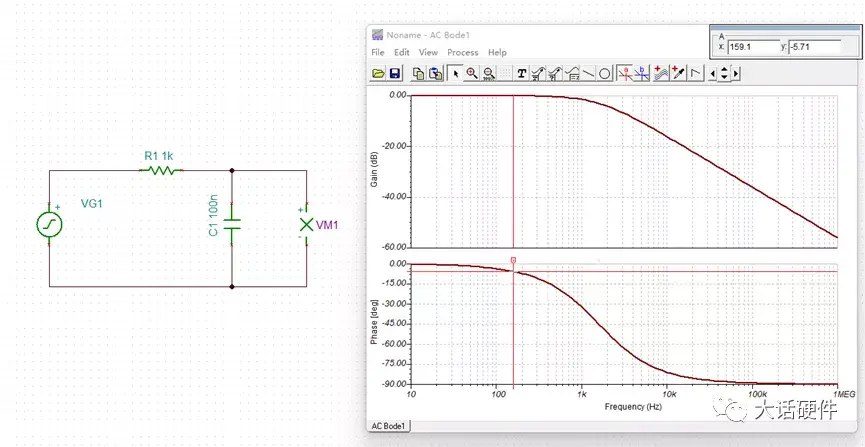
图22. 159.1Hz仿真波形分析波特图,输入信号频率为159.1Hz时,增益基本为-0.04dB,相移为-5.71°。此时输出信号和输入信号基本可认为是一样的,误差比较小。
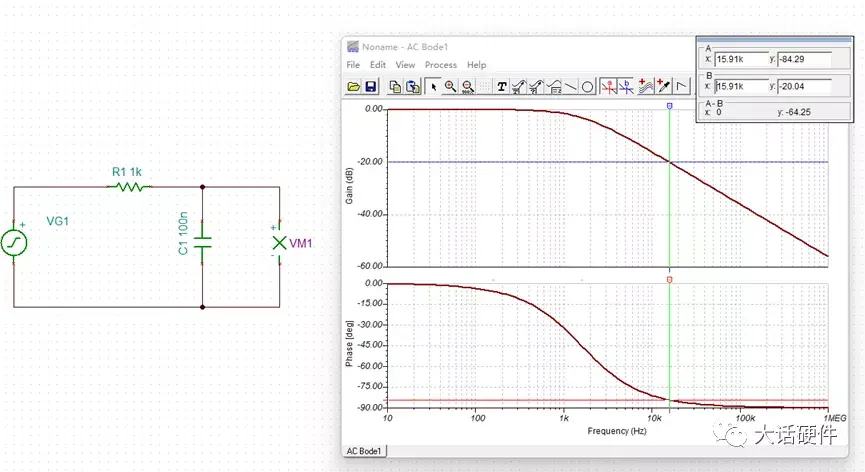
如果输入信号频率为10fo,仿真波形如下:
图23. 15.91KHz仿真波形分析波特图,输入信号频率为15.91KHz时,增益基本为-20.04dB,相移为-84.29°。此时输出信号为输入信号的0.0995倍,衰减的非常厉害。
7.总结
研究波特图增益和相位曲线并不是最终目的,它仅仅是我们分析一个电路对输入信号频率响应的手段。
通过观察波特图的增益和相位曲线,可以很好的分析出输出信号在不同频率点上增益是多大,那么就知道到底能提取出来多大的输入信号。分析出输出信号在不同频率点的相移,可以知道系统是否有产生自激振荡的风险。
对于滤波器来说,如果知道该滤波器的波特图,那么无论输入多大频率的信号,都可以计算出输出信号有多大,相位是怎样变化,从而很轻松的达到了我们想要的结果。
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/93486.html