二叉排序树的定义是递归定义吗_二叉排序树的定义是递归定义吗

《数据结构》复习7 树【下】
　　八、树的存储结构

　　8.1 树的逻辑结构

　　树是一种递归定义的数据结构

　　8.2 双亲表示法（顺序存储）

　　

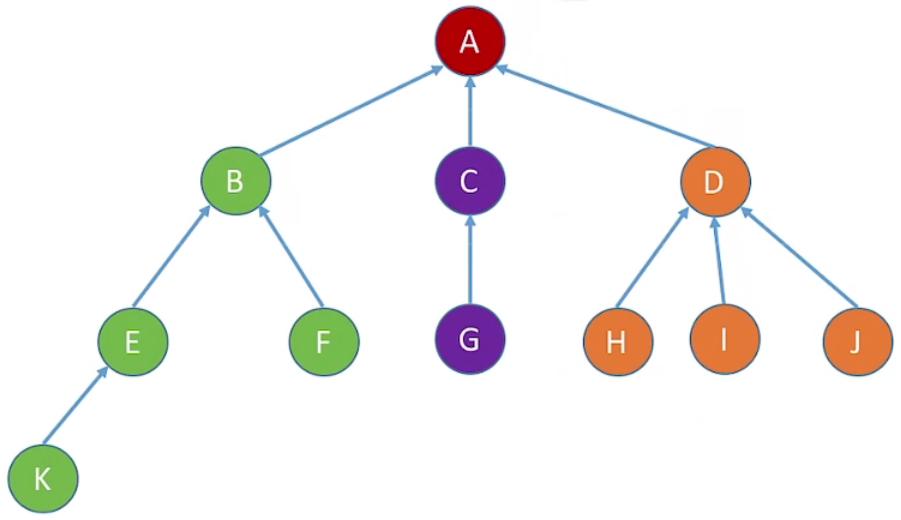
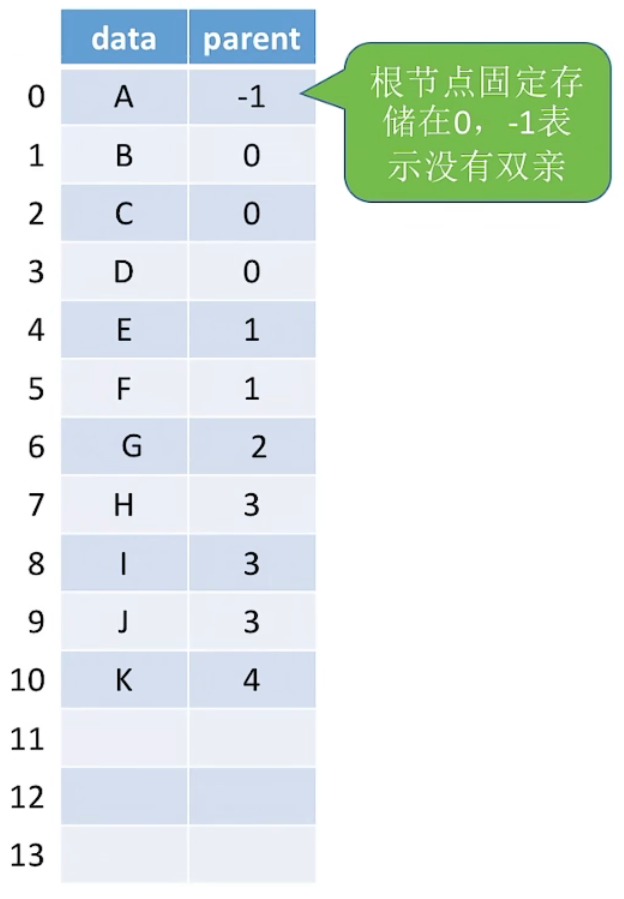
　　1、双亲表示法：每个节点中保存指向双亲的“指针”

　　2、图示：

　　3、代码

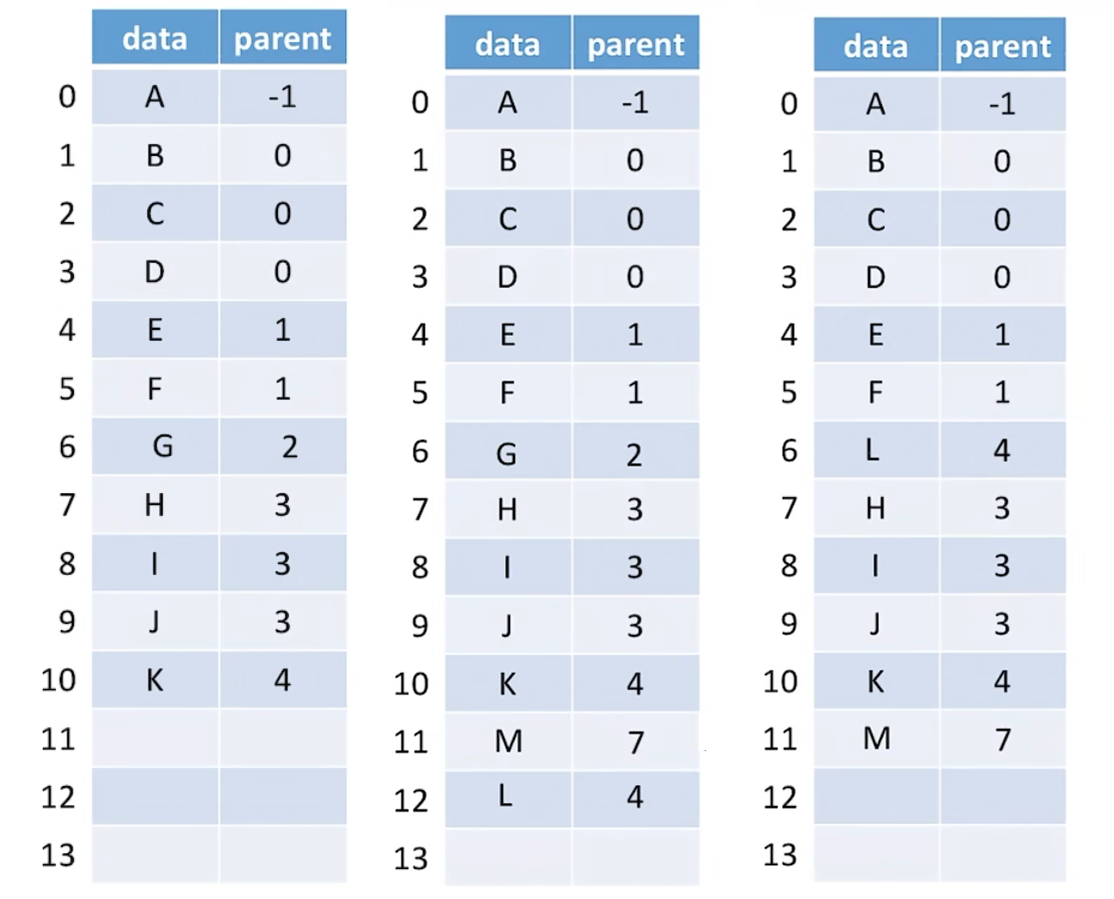
　　4、增加和删除结点

　　(1) 删除叶子结点

　　(2) 非叶子结点

　　需要删除所有的孩子结点。

　　5、寻找孩子结点

　　顺序存储查询指定结点的双亲很方便，查指定结点的孩子只能从头遍历

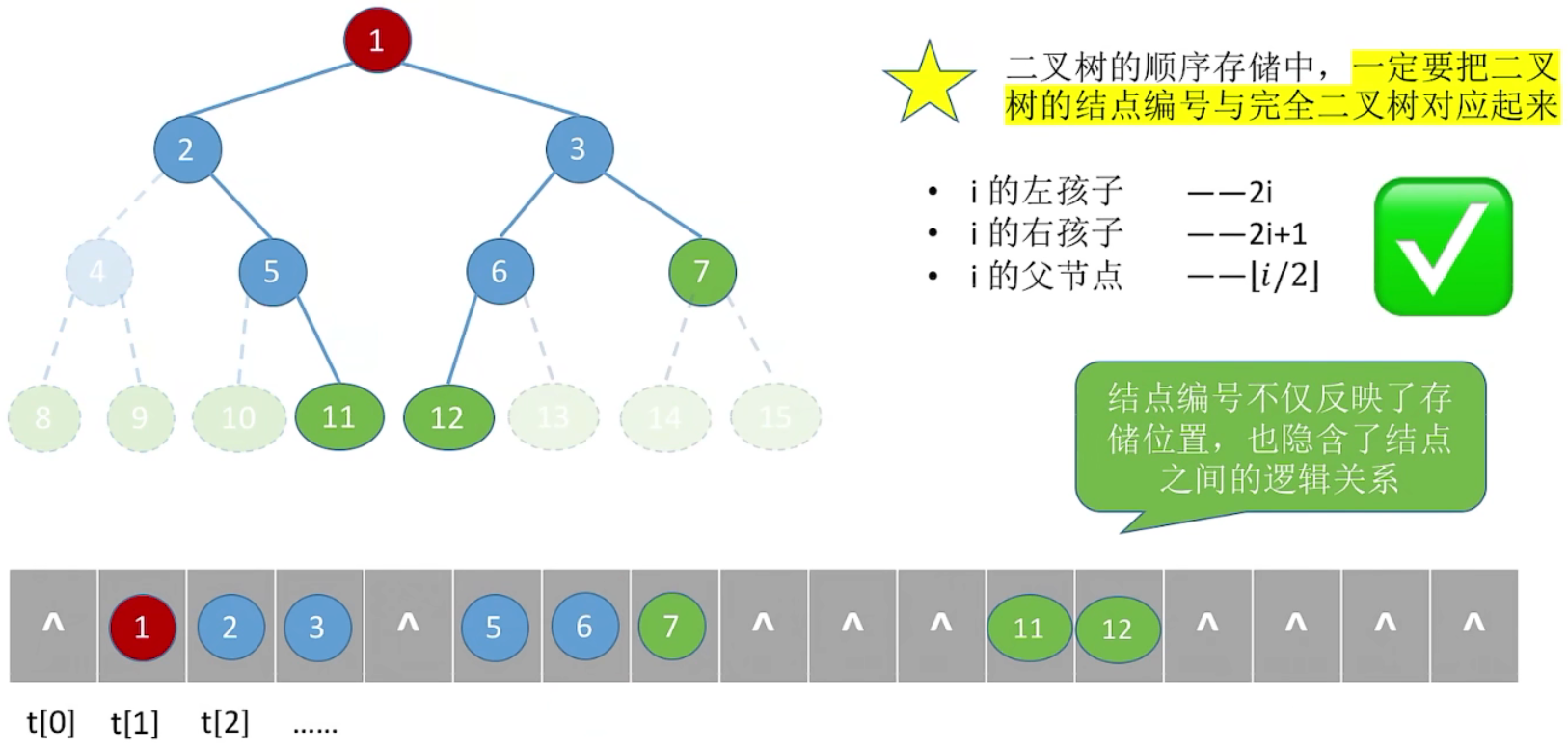
　　6、回顾二叉树的顺序存储

　　双亲表示法存储二叉树也可以

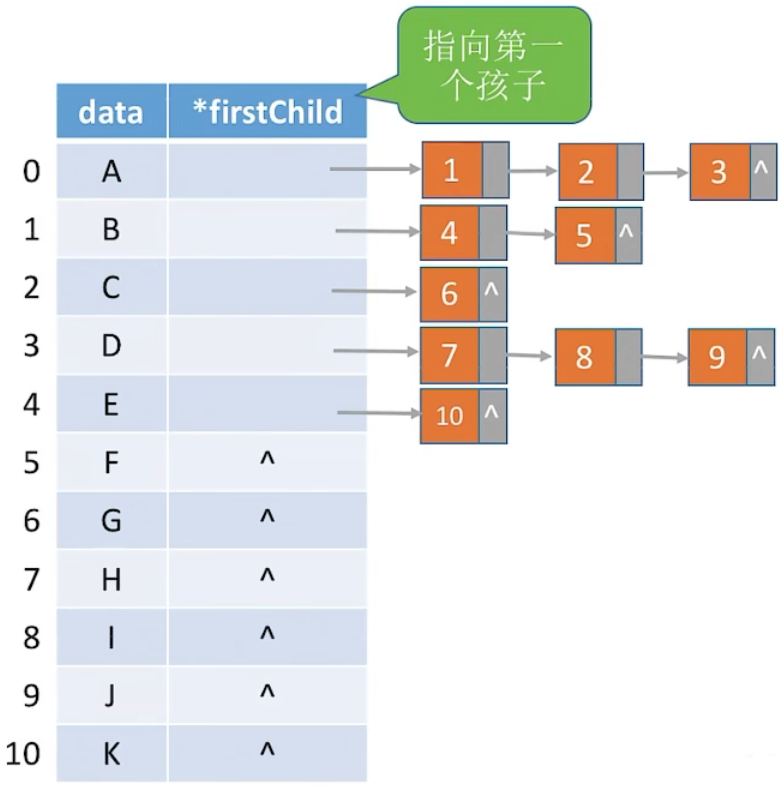
　　8.3 孩子表示法（顺序 + 链式存储）

　　1、图示

　　2、代码

　　3、评价：

　　找孩子方便，找双亲不方便

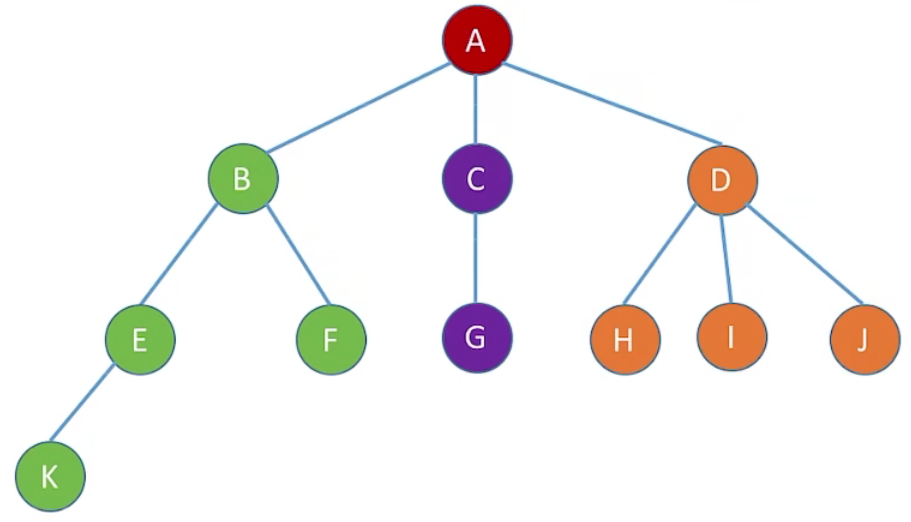
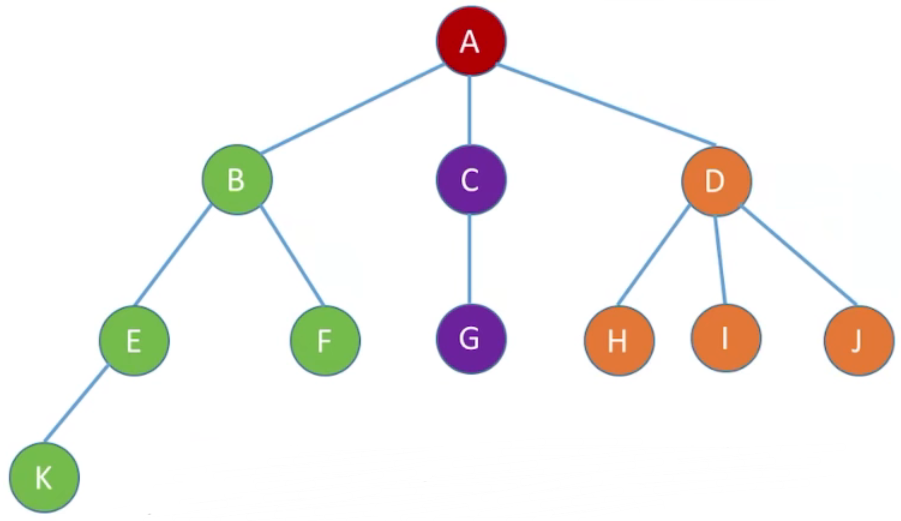
　　8.4 孩子兄弟表示法（链式存储）

　　1、代码

　　2、图示

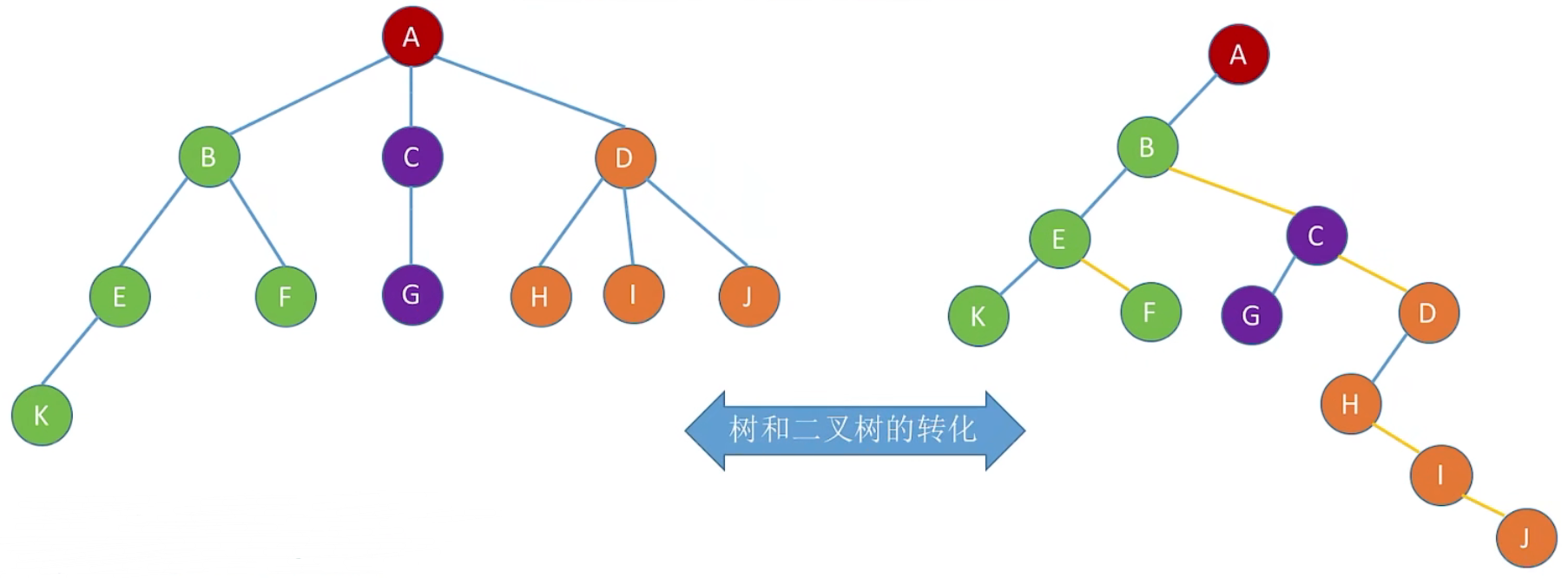
　　A 的 firstchild 指向 B，nextsibling 指向 NULL

　　B 的 firstchild 指向 E，nextsibling 指向 C

　　C 的 firstchild 指向 G，nextsibling 指向 D

　　3、优点：可以用我们熟悉的二叉树操作来处理树

　　4、二叉树转化成树：

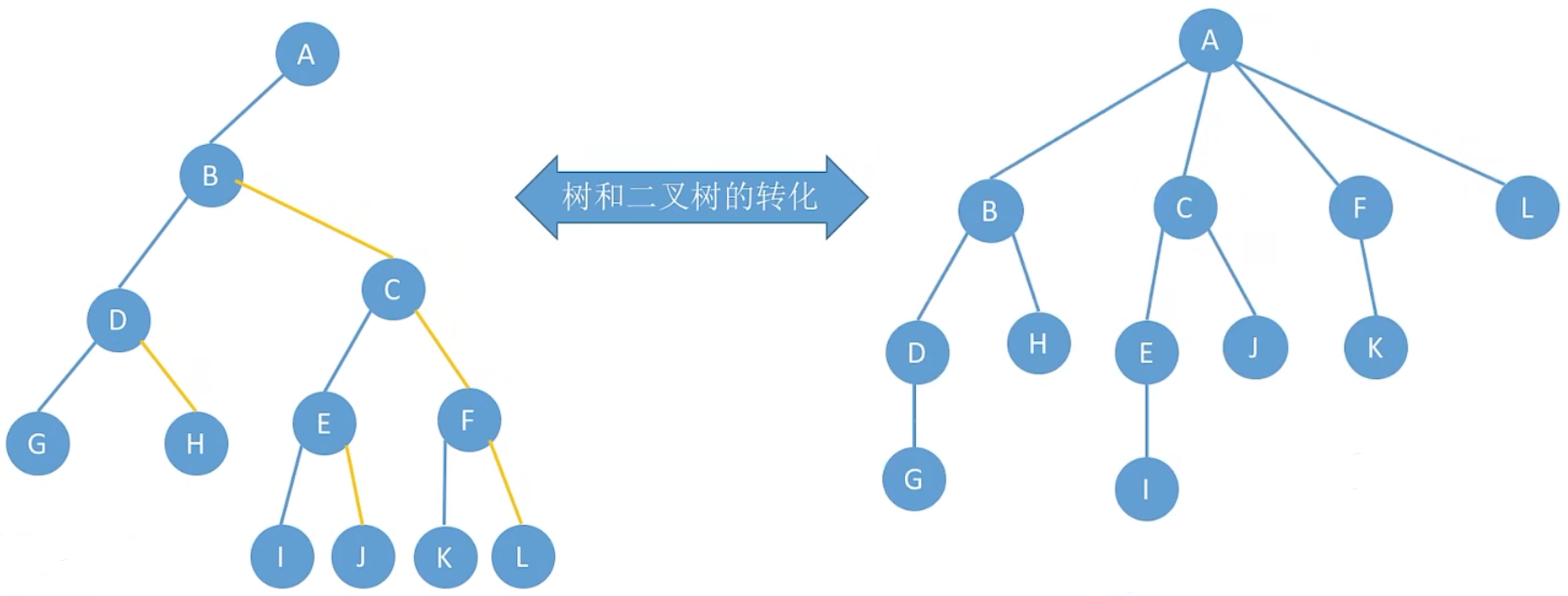
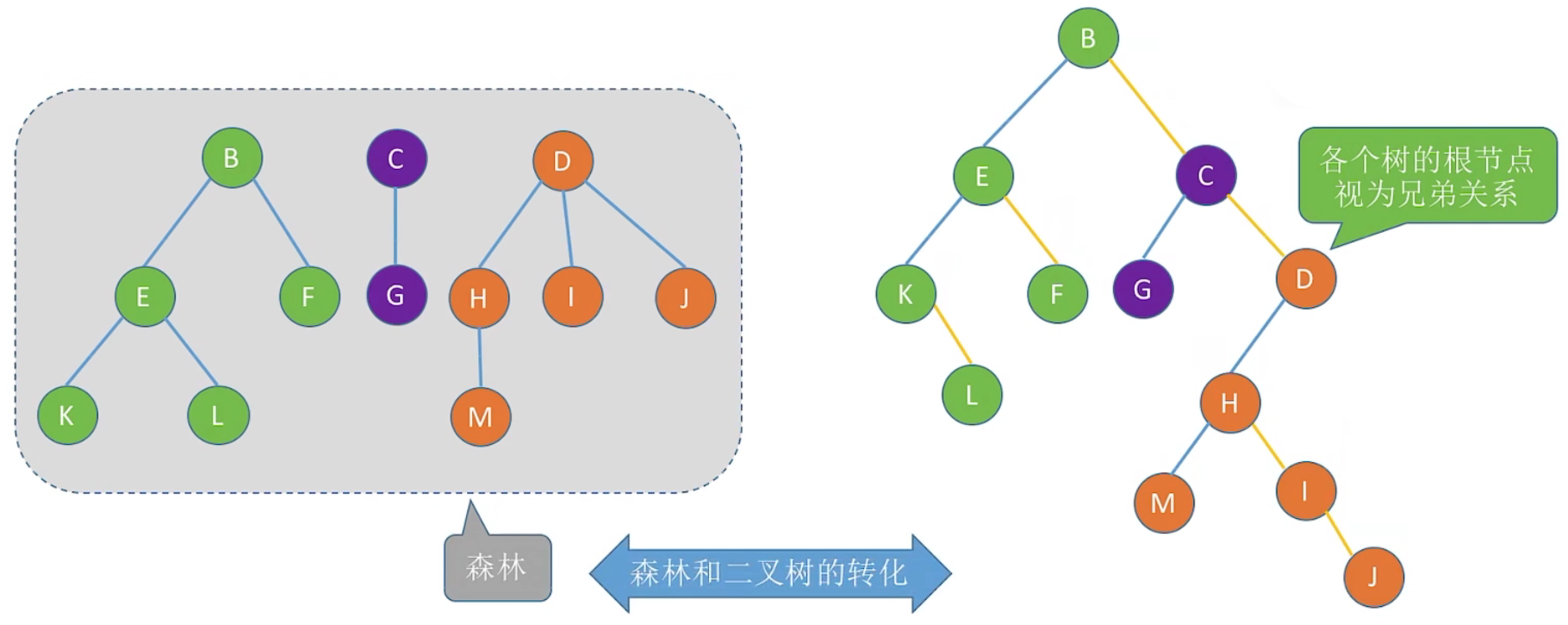
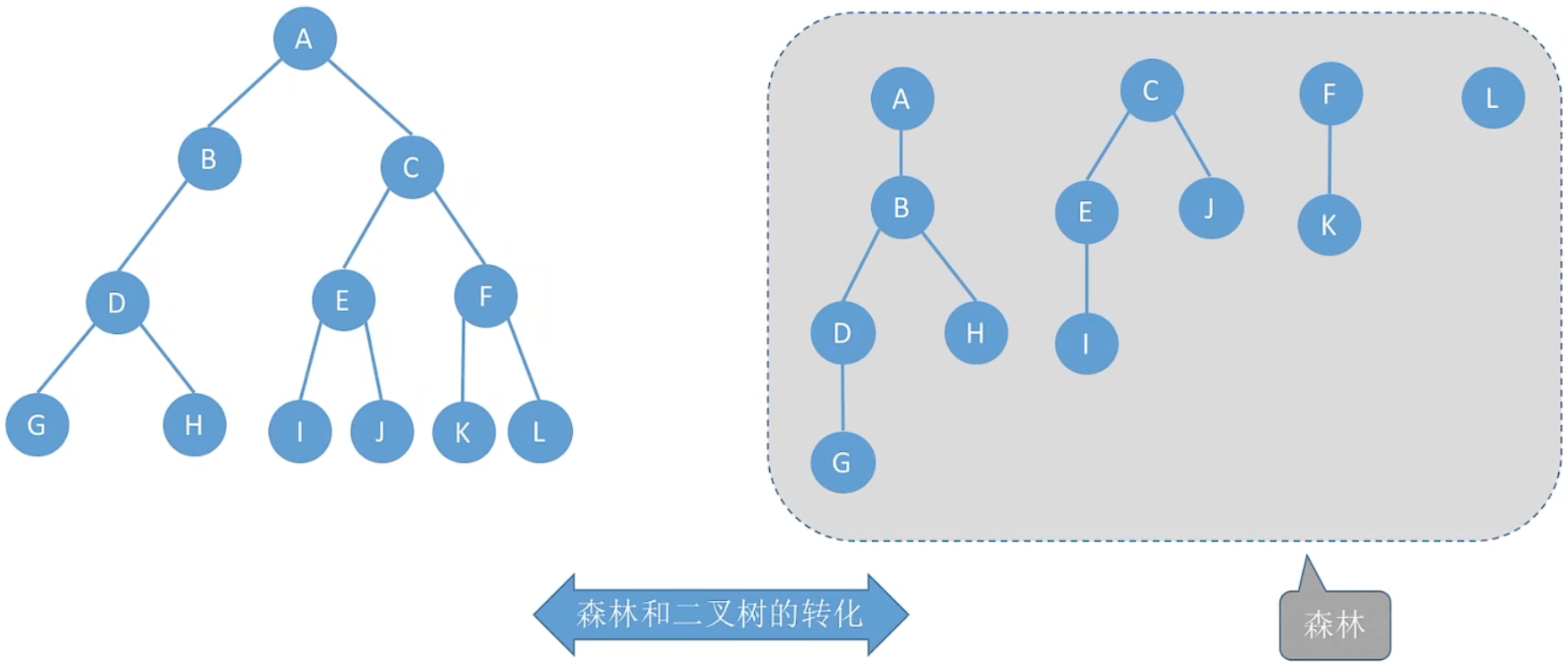
　　8.5 森林和二叉树的转化

　　1、森林：是 m (m ≥ 0) 棵互不相交的树的集合

　　2、森林转化成二叉树

　　可以把各个树的根节点视为兄弟关系

　　3、二叉树转化成森林

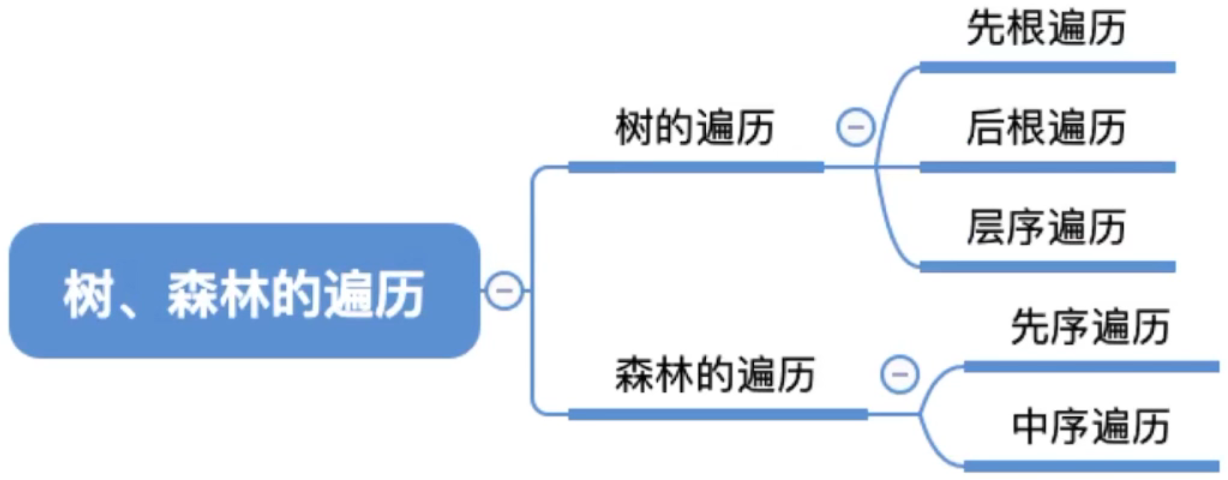
　　九、树、森林的遍历

　　

　　先根/后根遍历被称为深度优先遍历

　　层次遍历称为广度优先遍历

　　9.1 先根遍历

　　1、操作：若树非空，先访问根结点，再依次对每棵子树进行先根遍历。

　　2、代码

　　3、图示

　　树的先遍历序列与这棵树对应二叉树的先序序列相同。

　　9.2 根的后根遍历

　　1、操作：若树非空，先依次对每棵子树进行后根遍历，最后再访问根结点。

　　2、代码

　　3、图示

　　树的后根遍历序列与这棵树相应二叉树的中序序列相同。

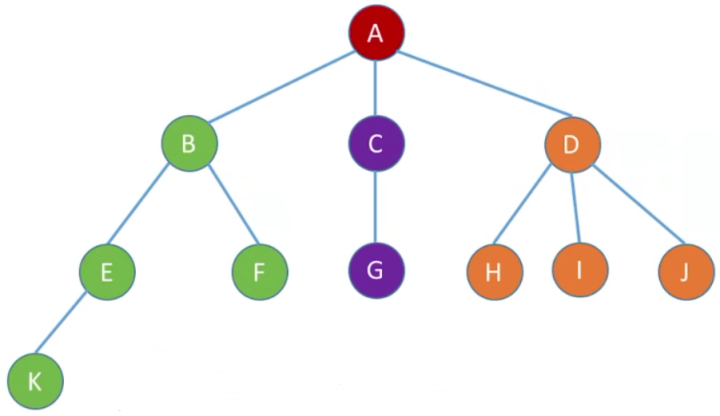
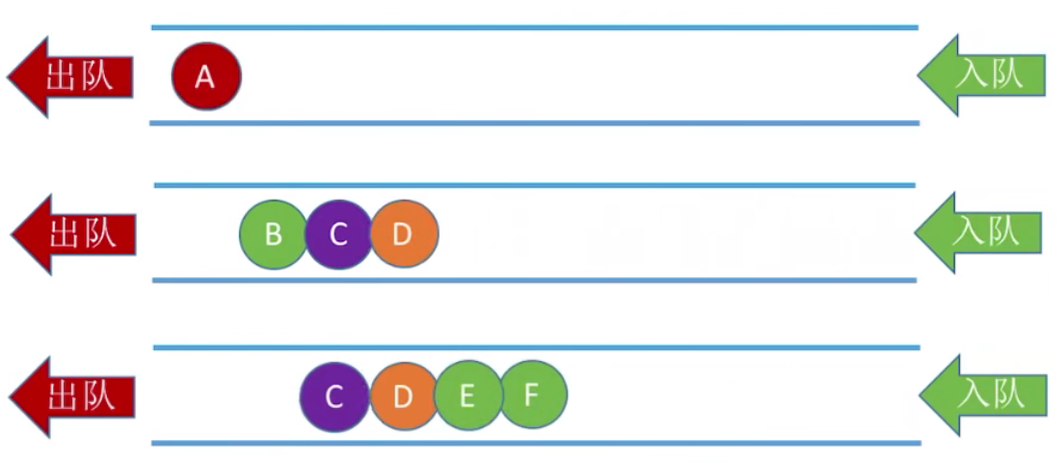
　　9.3 树的层次遍历

　　1、层次遍历（用队列实现）

　　① 若树非空，则根节点入队

　　② 若队列非空，队头元素出队并访问，同时将该元素的孩子依次入队

　　③ 重复 ② 直到队列为空

　　2、图示

　　9.4 森林的先序遍历

　　一棵树去掉根节点后，其各个子树组成森林。

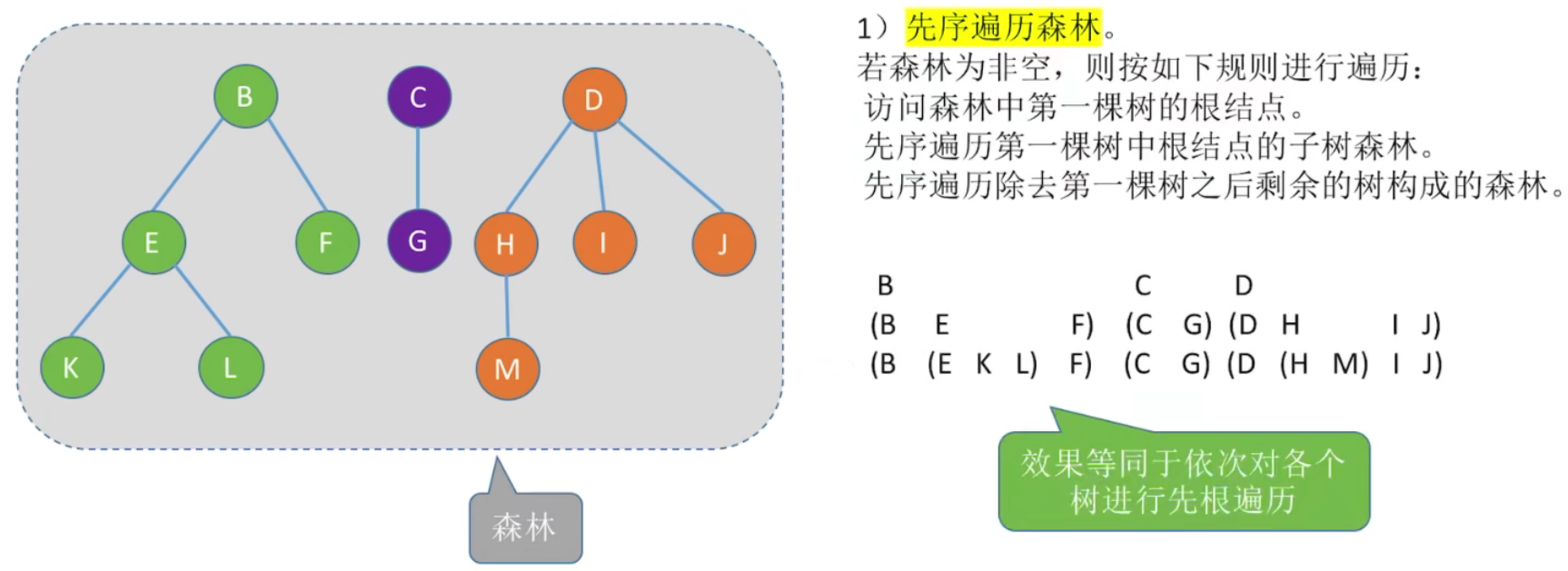
　　1、先序遍历森林

　　若森林为非空，则按如下规则进行遍历：

　　访问森林中第一棵树的根结点。

　　先序遍历第一棵树中根结点的子树森林。

　　先序遍历除去第一棵树之后剩余的树构成的森林。

　　2、图示：

　　9.5 森林的中序遍历

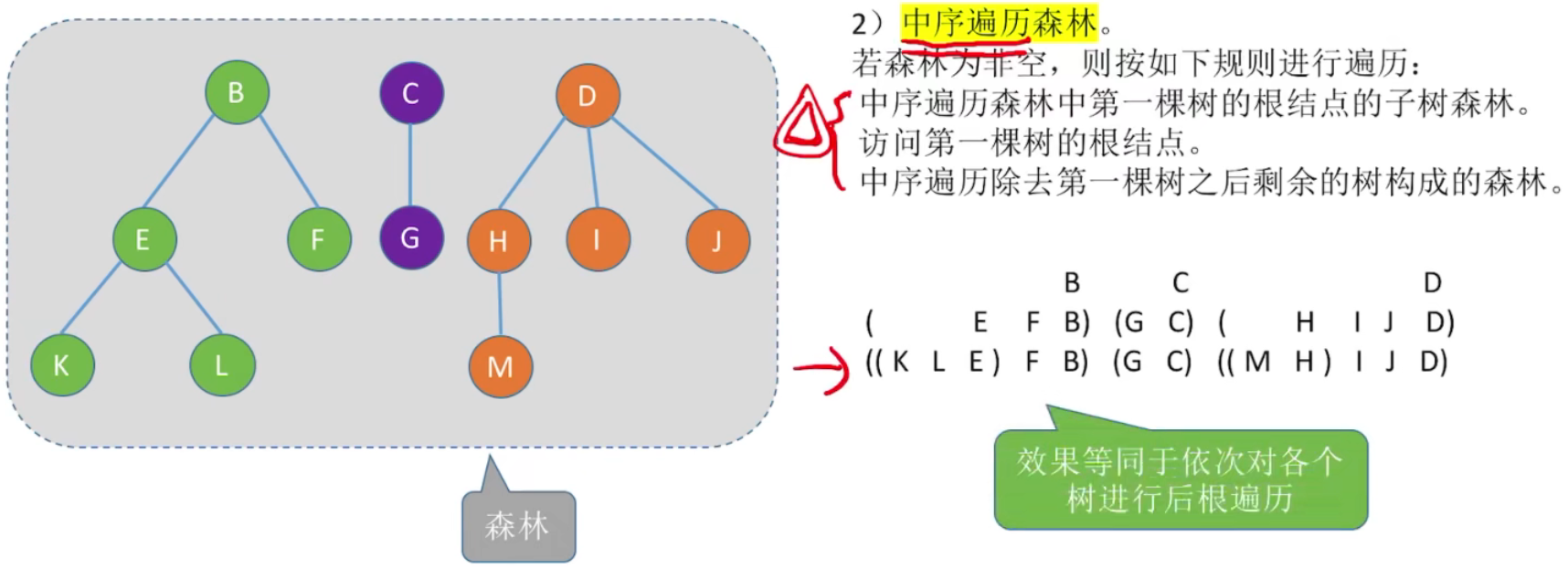
　　1、中序遍历森林

　　若森林为非空，则按如下规则进行遍历：

　　中序遍历森林中第一棵树的根结点的子树森林。

　　访问第一棵树的根结点。

　　中序遍历除去第一棵树之后剩余的树构成的森林。

　　2、图示：

　　9.6 总结

　　树森林二叉树先根遍历先序遍历先序遍历后根遍历中序遍历中序遍历

　　十、二叉排序树

　　10.1 二叉排序树定义

　　1、二叉排序树，又称二叉查找树 ( BST，Binary Search Tree )

　　2、一棵二叉树或者是空二叉树，或者是具有如下性质的二叉树：

　　左子树上所有结点的关键字均小于根结点的关键字；

　　右子树上所有结点的关键字均大于根结点的关键字。

　　左子树和右子树又各是一棵二叉排序树。

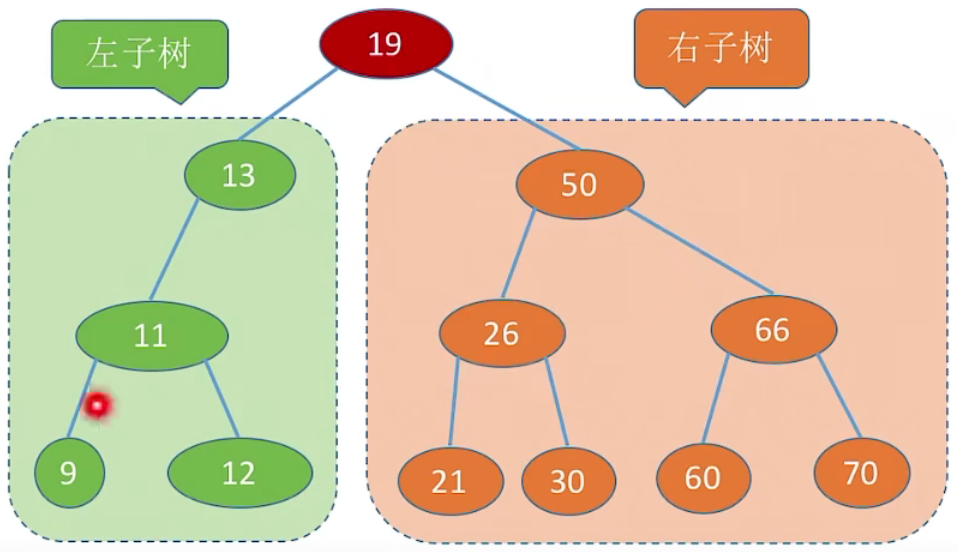
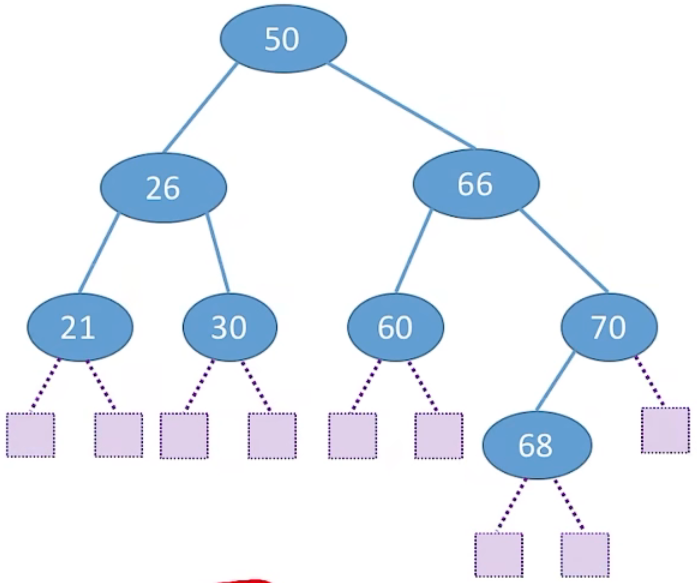
　　3、图示：

　　4、左子树节点值 < 根节点值 < 右子树节点值

　　进行中序遍历，可以得到一个递增的有序序列

　　二叉排序树可用于元素的有序组织、搜索

　　10.2 二叉排序树的查找

　　1、左子树结点值 < 根结点值 < 右子树结点值

　　2、若树非空，目标值与根结点的值比较：

　　若相等，则查找成功;

　　若小于根结点，则在左子树.上查找，否则在右子树上查找。

　　查找成功，返回结点指针；查找失败返回 NULL

　　3、代码（顺序实现）

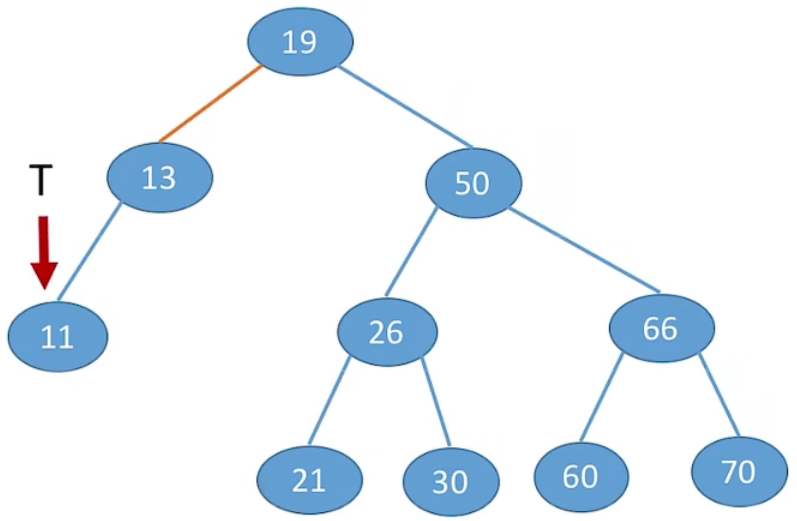
　　4、图示

　　如果输入的是 12，最后指针指向的是 11 的右孩子，也就是 NULL

　　4、代码（递归实现）

　　10.3 二叉排序树的插入和构造

　　1、插入：

　　若原二叉排序树为空，则直接插入结点；否则，若关键字 k 小于根结点值，则插入到左子树，若关键字 k 大于根结点值，则插入到右子树

　　2、构造：

　　不同的关键字序列可能得到同款二叉排序树

　　也可能得到不同款二叉树

　　按照序列 str = { 50, 66, 60, 26, 21, 30, 70, 68 }、str = { 50, 26, 21, 30, 66, 60, 70, 68 } 建立 BST

　　按照序列 str = {26, 21, 30, 50, 60, 66, 68, 70} 建立 BST

　　3、代码

　　C语言指针太难了，用 C++ 引用实现

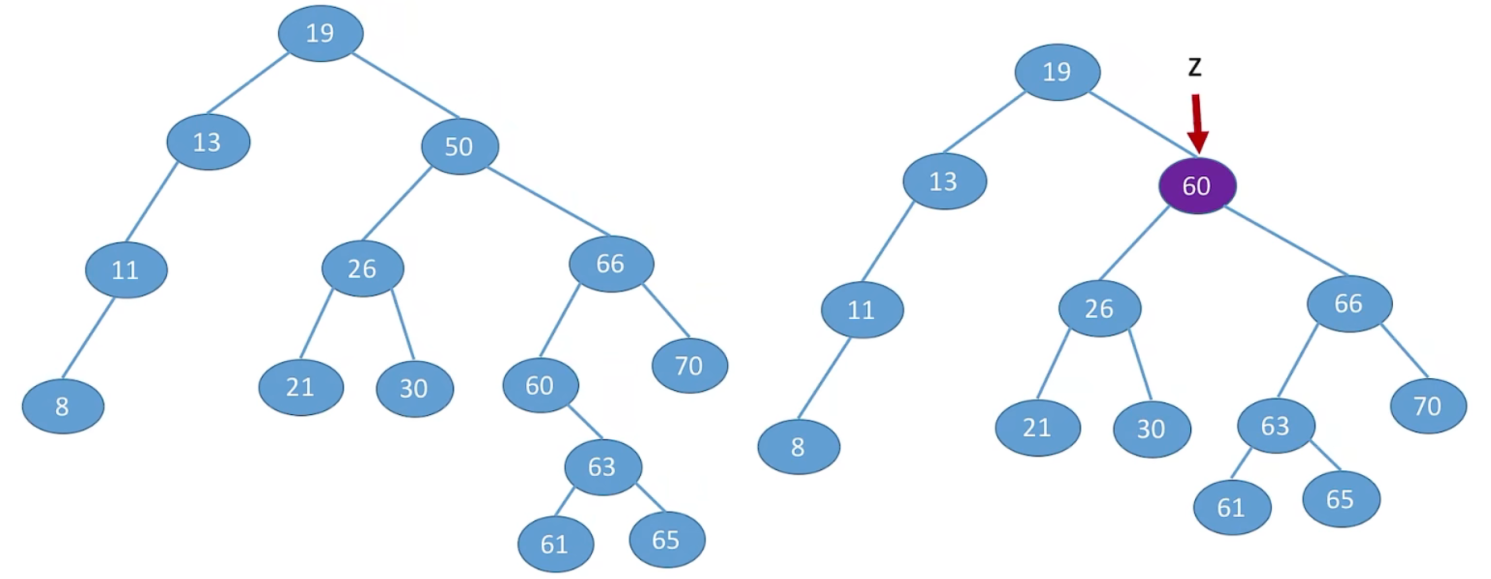
　　10.4 二叉排序树的删除

　　1、先搜索找到目标结点：

　　(1) 若被删除结点 z 是叶结点，则直接删除，不会破坏二叉排序树的性质。

　　(2) 若结点 z 只有一棵左子树或右子树，则让 z 的子树成为 z 父结点的子树，替代 z 的位置。

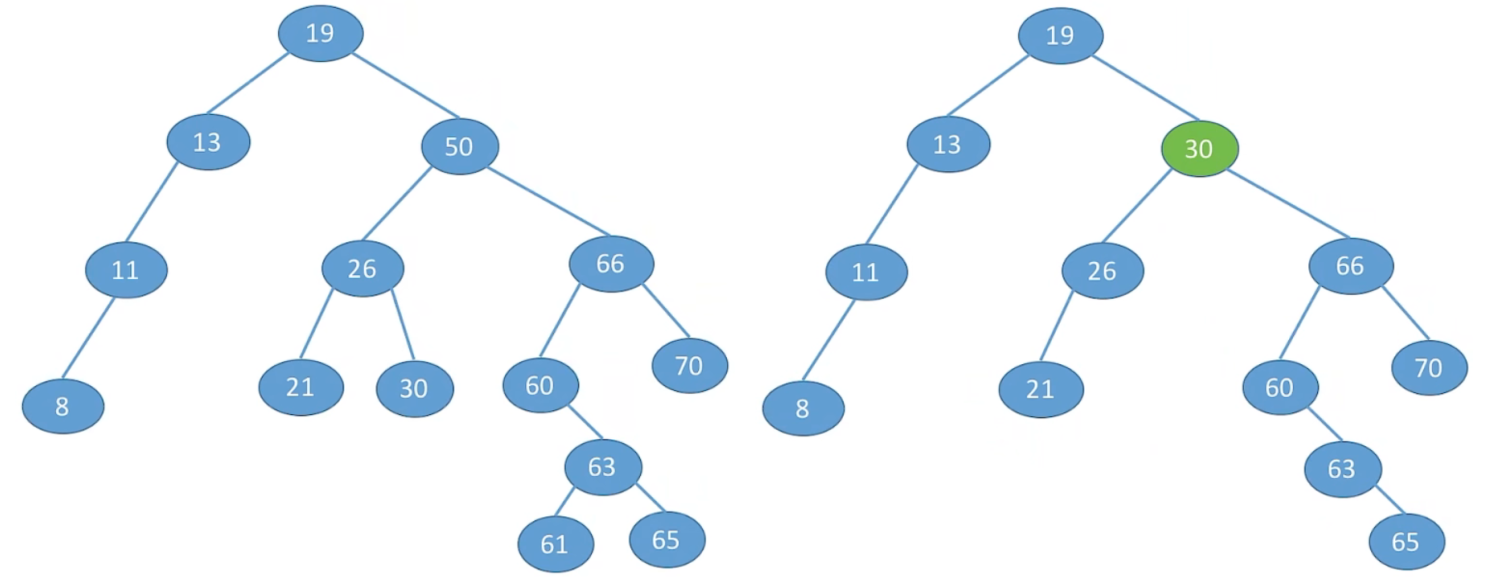
　　(3) 若结点z有左、右两棵子树，则令 z 的直接后继 (或直接前驱) 替代 z，然后从二叉排序树中删去这

　　个直接后继 (或直接前驱)，这样就转换成了第一或第二种情况。

　　① z 的后继：z 的右子树中最左下结点 (该节点定没有左子树)

　　左子树结点值 < 根结点值 < 右子树结点值

　　进行中序遍历，可以得到一个递增的有序序列

　　② z 的前驱：z 的左子树中最右下结点 (该节点一定没有右子树)

　　2、代码（伪代码）

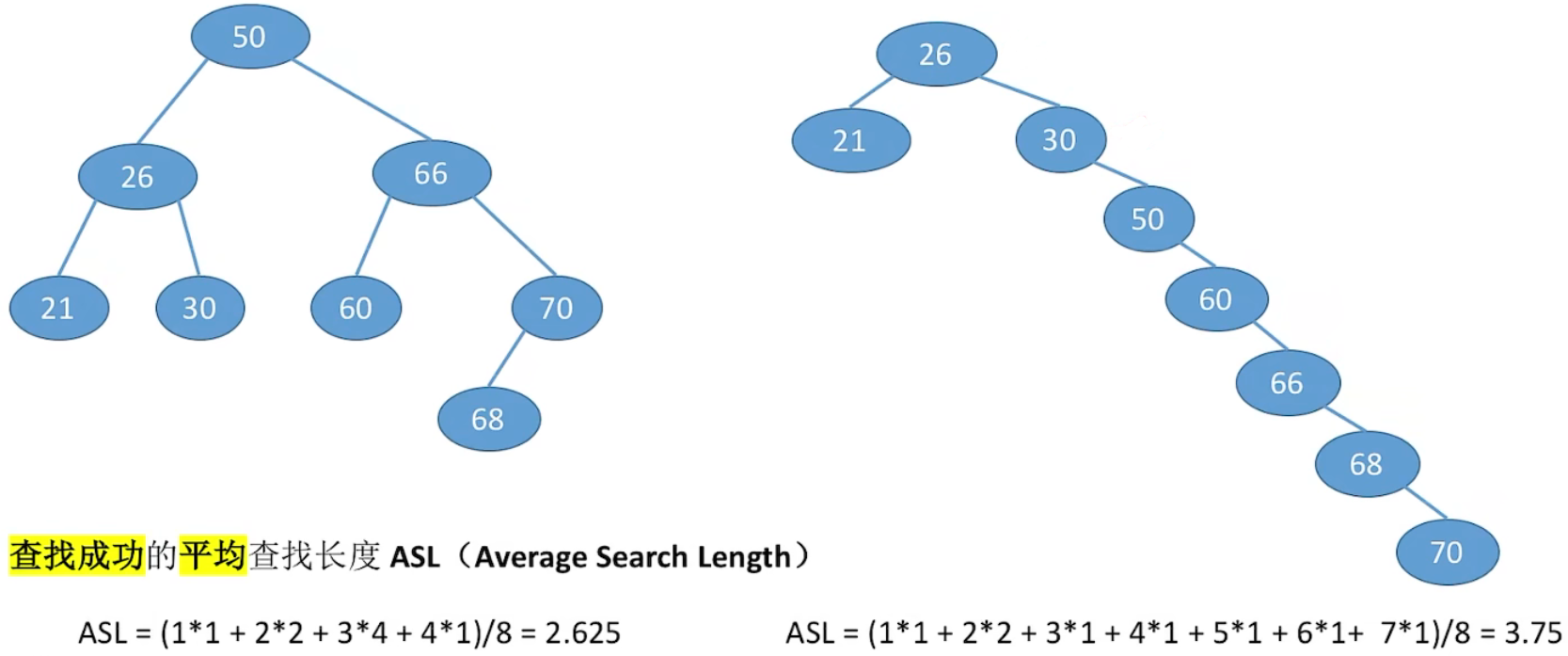
　　10.5 查找效率分析

　　1、查找长度：

　　在查找运算中，需要对比关键字的次数称为查找长度，反映了查找操作时间复杂度

　　2、查找成功的平均查找长度 ASL

　　3、最好情况：

　　n 个结点的二叉树最小高度为

　　平均查找长度 = O( )

　　4、最坏情况：

　　每个结点只有一个分支，树高 h = 节点数 n。平均查找长度 = O(n)

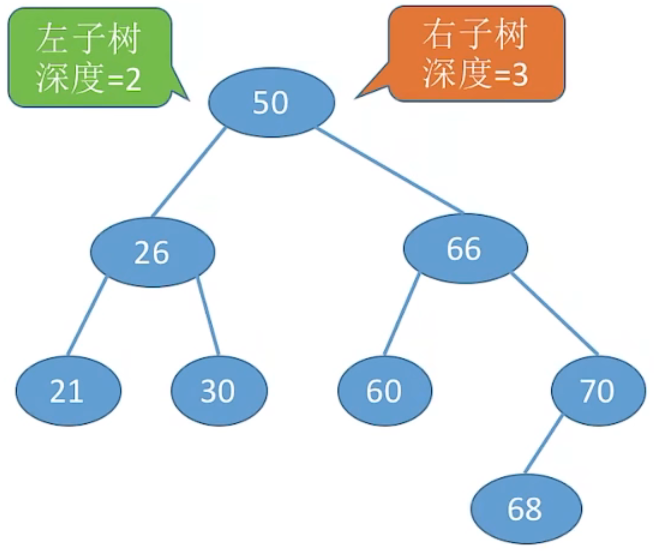
　　5、平衡二叉树

　　树上任一结点的左子树和右子树的深度之差不超过 1。

　　6、查找失败的平均查找长度 ASL

　　ASL = (3 * 7 +4 * 2) / 9

　　十一、平衡二叉树

　　11.1 定义

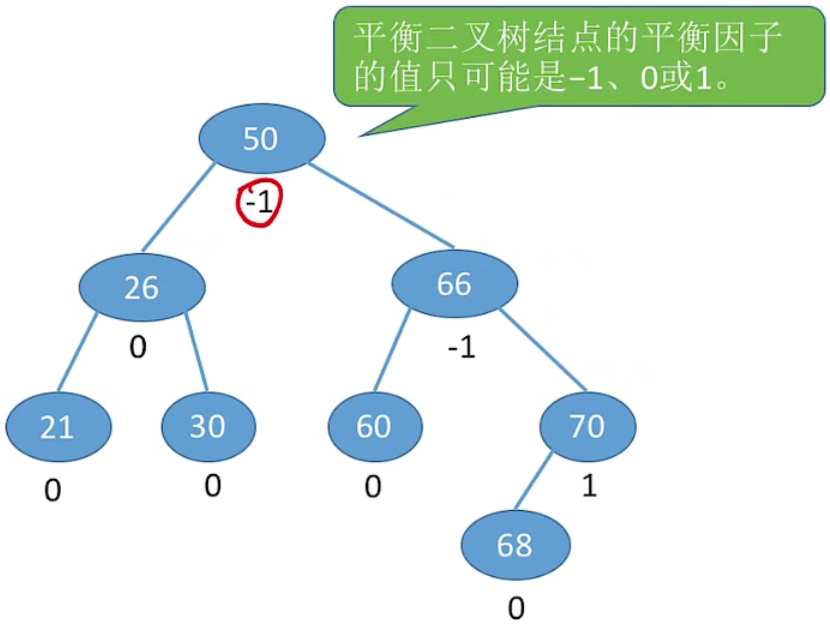
　　1、平衡二叉树 (Balanced BinaryTree)，简称平衡树 (AVL树) —— 树上任一结点的左子树和右子树的高度之差不超过 1。

　　2、结点的平衡因子 = 左子树高 – 右子树高

　　3、代码

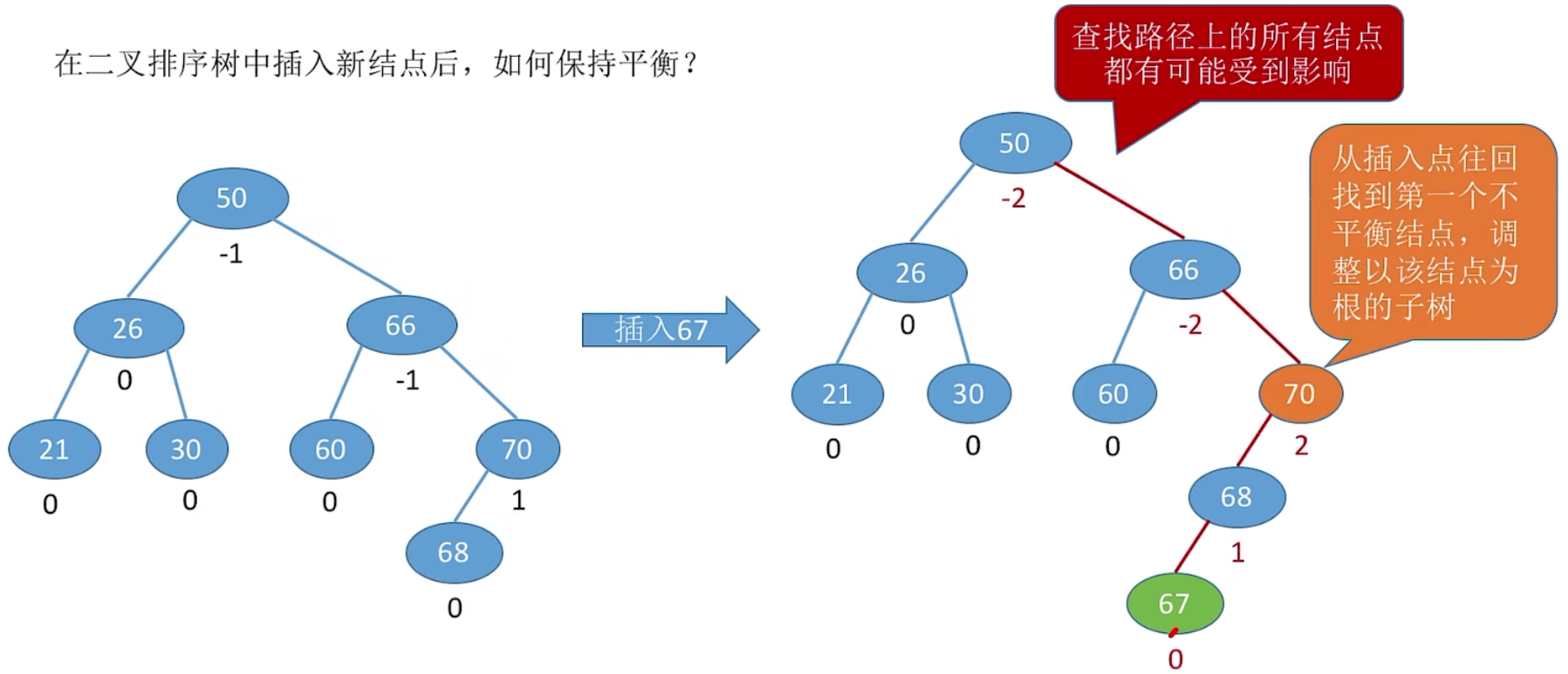
　　11.2 二叉排序树中插入新结点后，如何保持平衡？

　　

　　每次调整的对象都是“最小不平衡子树”

　　

　　11.3 调整最小不平衡子树

　　

　　11.4 LL 和 RR 的情况

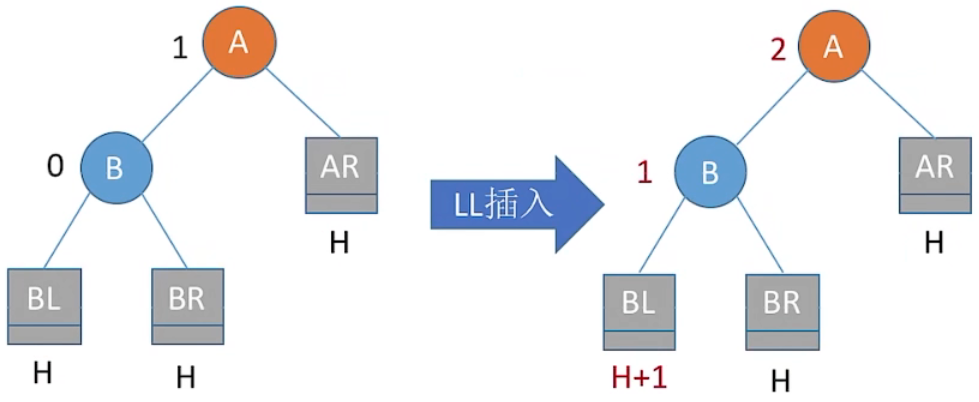
　　1、假定 A 是最小不平衡子树

　　2、目标：恢复平衡；保持二叉排序树特性

　　3、二叉排序树的特性：

　　左子树结点值 < 根结点值 < 右子树结点值

　　BL < B < BR < A < AR

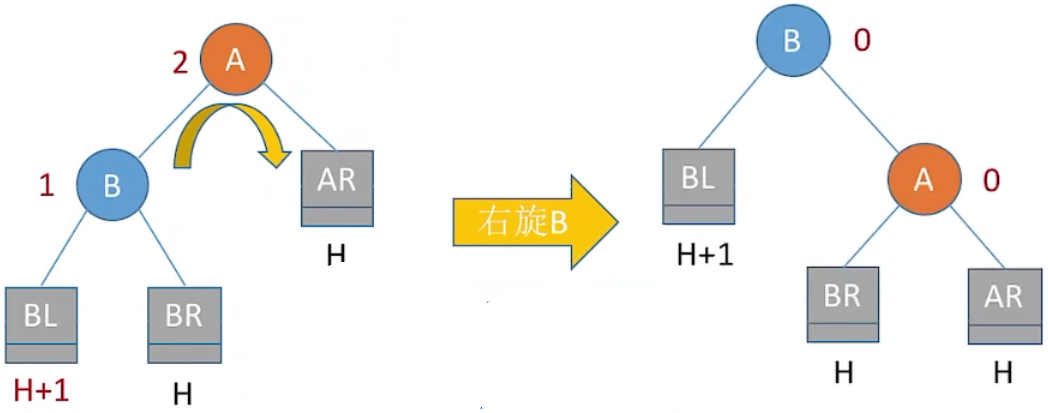
　　4、LL 平衡旋转 (右单旋转)

　　由于在结点 A 的左孩子 (L) 的左子树 (L)，上插入了新结点，A 的平衡因子由 1 增至 2，导致以 A 为根的子树失去平衡，需要一次向右的旋转操作。将 A 的左孩子 B 向右上旋转代替 A 成为根结点，将 A 结点向右下旋转成为 B 的右子树的根结点，而 B 的原右子树则作为 A 结点的左子树。

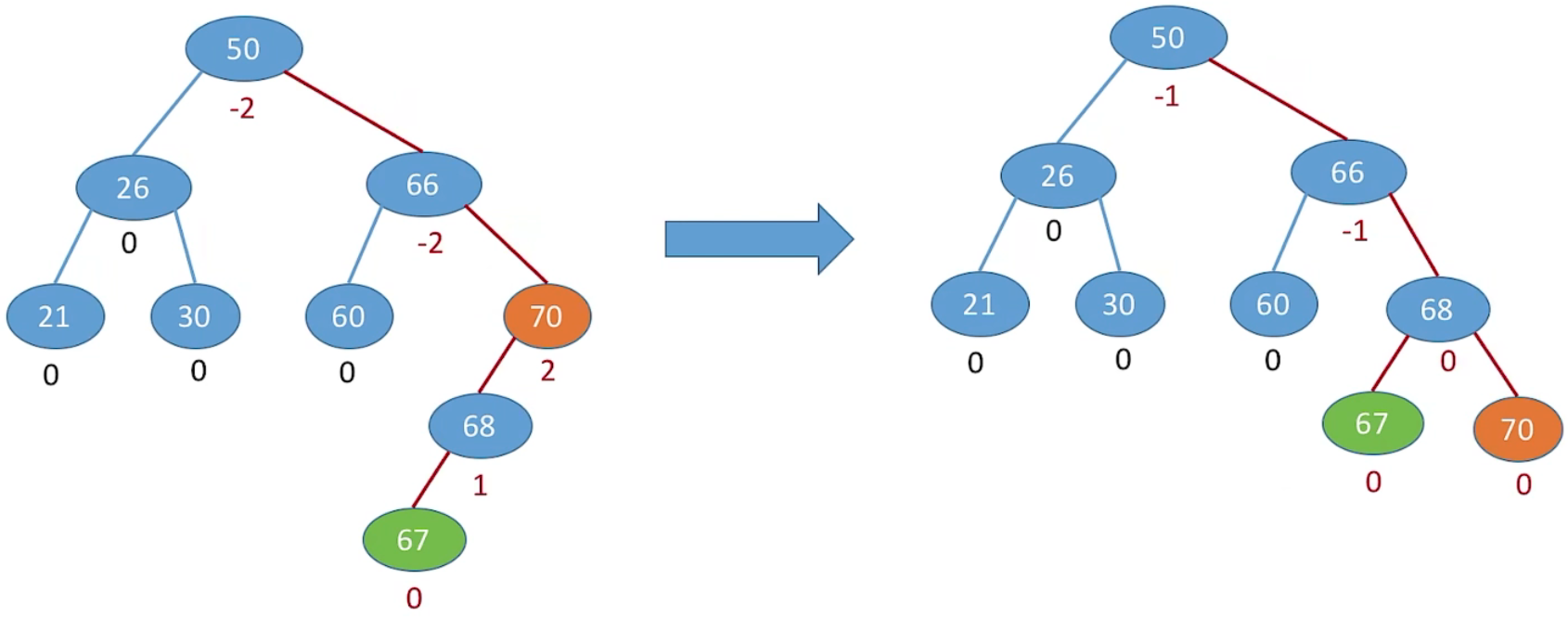
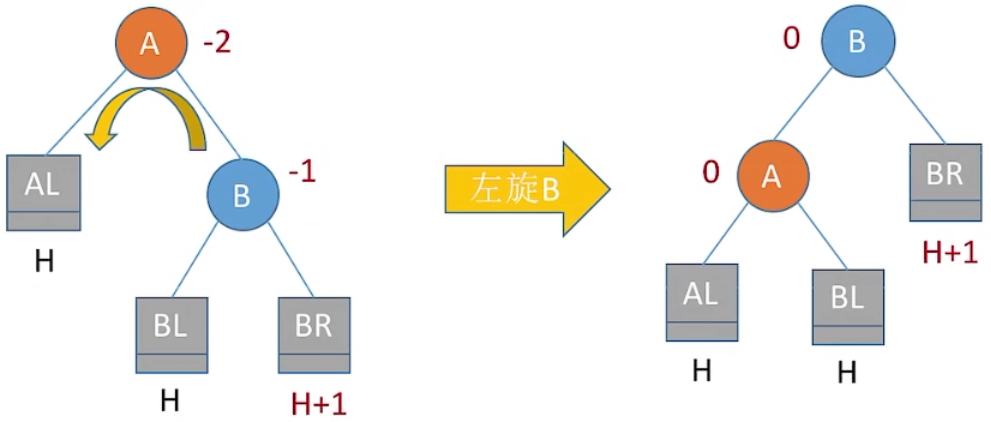
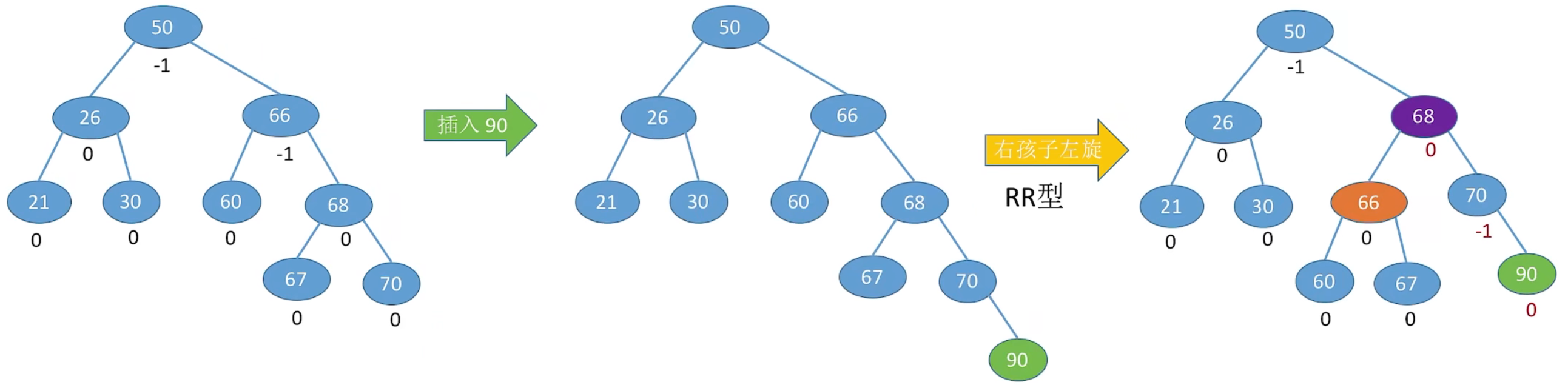
　　5、RR 做平衡旋转 (左单旋转)

　　由于在结点A的右孩子 (R) 的右子树 (R) 上插入了新结点，A 的平衡因子由 -1 减至 -2，导致以 A 为根的子树失去平衡，需要一次向左的旋转操作。将 A 的右孩子 B 向左上旋转代替 A 成为根结点，将 A 结点向左下旋转成为 B 的左子树的根结点，而 B 的原左子树则作为 A 结点的右子树。

　　6、代码思路

　　(1) 实现 f 向右下旋转，p 向右上旋转：

　　其中 f 是爹，p 为左孩子，gf 为 f 的父节点

　　① f->lchild = p->rchild;

　　② p->rchild = f;

　　③ gf->lchild/rchild = p;

　　(2) 实现 f 向左下旋转，p 向左上旋转：

　　其中 f 是爹，p 为右孩子，gf 为 f 的父节点

　　① f->rchild = p->lchild;

　　② p->Ichild = f;

　　③ gf->lchild/rchild = p;

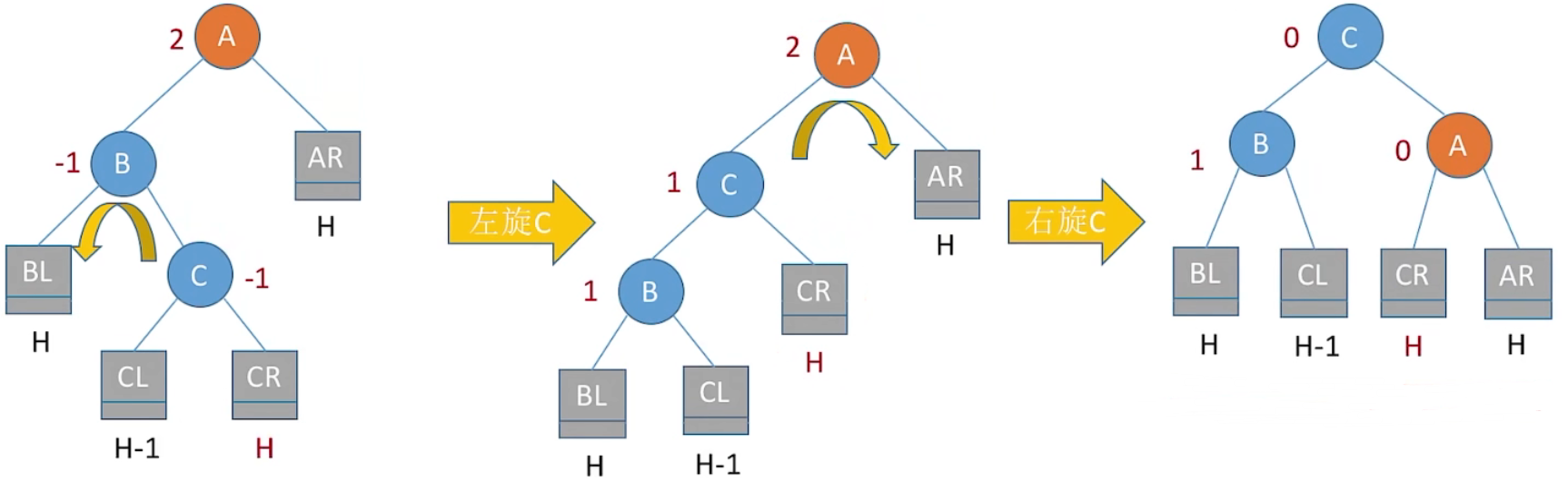
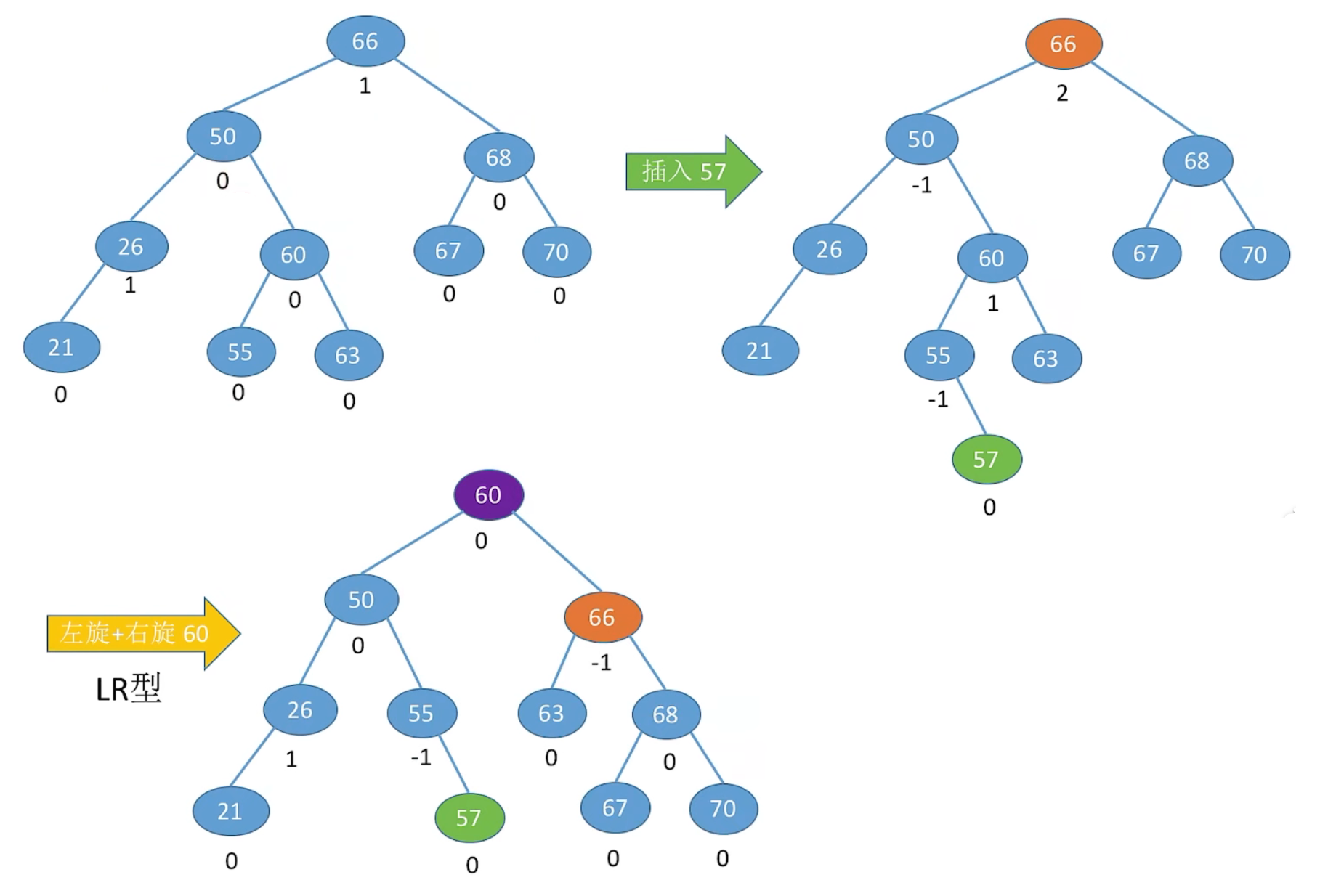
　　11.5 LR 和 RL 的情况

　　1、LR 平衡旋转 (先左后右双旋转)

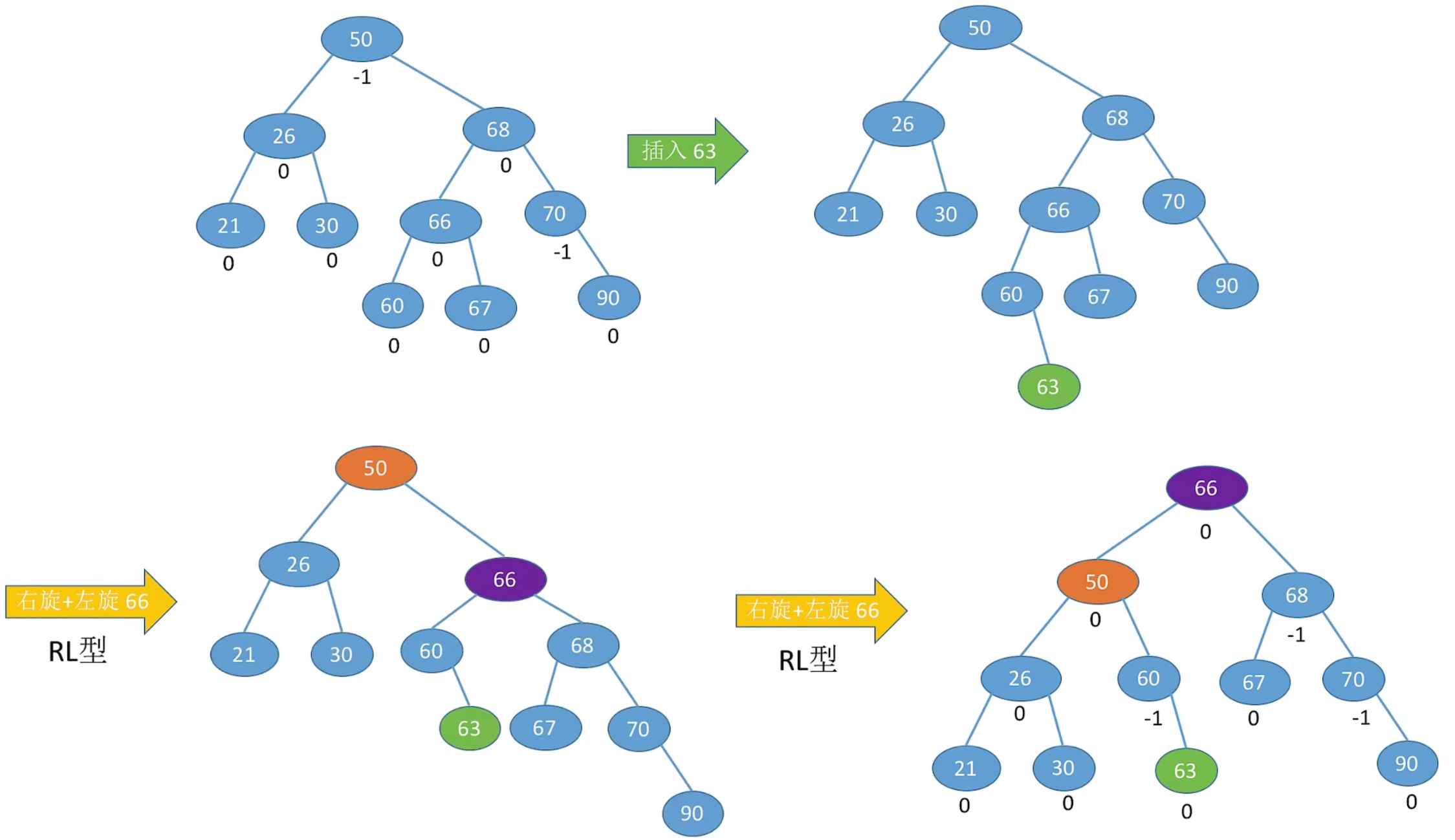
　　由于在 A 的左孩子 (L) 的右子树 (R)，上插入新结点，A 的平衡因子由 1 增至2，导致以 A 为根的子树失去平衡，需要进行两次旋转操作，先左旋转后右旋转先将 A 结点的左孩子 B 的右子树的根结点 C 向左上旋转提升到 B 结点的位置，然后再把该 C 结点向右上旋转提升到 A 结点的位置

　　BL < B < CL < C < CR < A < AR

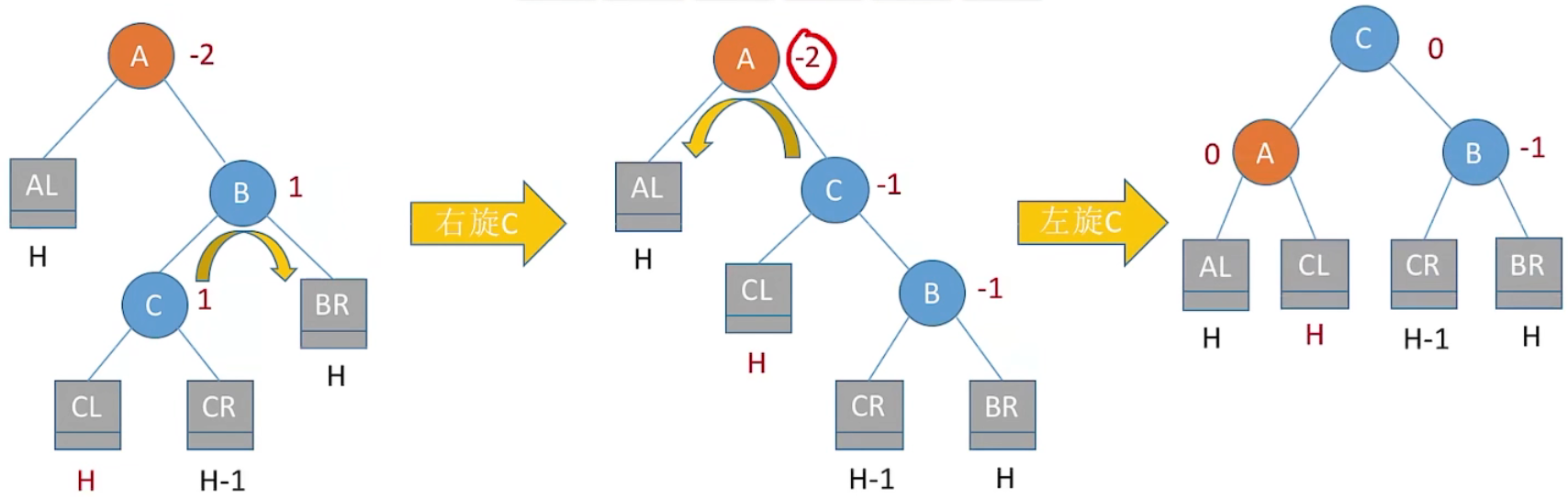
　　2、RL 平衡旋转 (先右后左双旋转)

　　AL < A < CL < CR < B < BR

　　11.6 小总结和练习

　　树高为 H+2，插入结点后变成 H+3，变换后又变成 H+ 2

　　插入操作导致“最小不平衡子树”高度+1，经过调整后高度恢复

　　练习1：

　　练习2：

　　练习3：

　　11.7 查找效率分析

　　若树高为h，则最坏情况下，查找一个关键字最多需要对比 h 次，即查找操作的时间复杂度不可能超过 O(h)

　　平衡二叉树一树上任一结点的左子树和右子树的高度之差不超过 1。

　　假设以 表示深度为 h 的平衡树中含有的最少结点数。

　　则有 = 0, = 1, = 2，并且有

　　可以证明含有 n 个结点的平衡二叉树的最大深度为 平衡二叉树的平均查找长度为

　　十二、哈夫曼树

　　12.1 带权路径长度

　　1、结点的权：

　　有某种现实含义的数值 (如：表示结点的重要性等)

　　2、结点的带权路径长度：

　　从树的根到该结点的路径长度 (经过的边数) 与该结点上权值的乘积

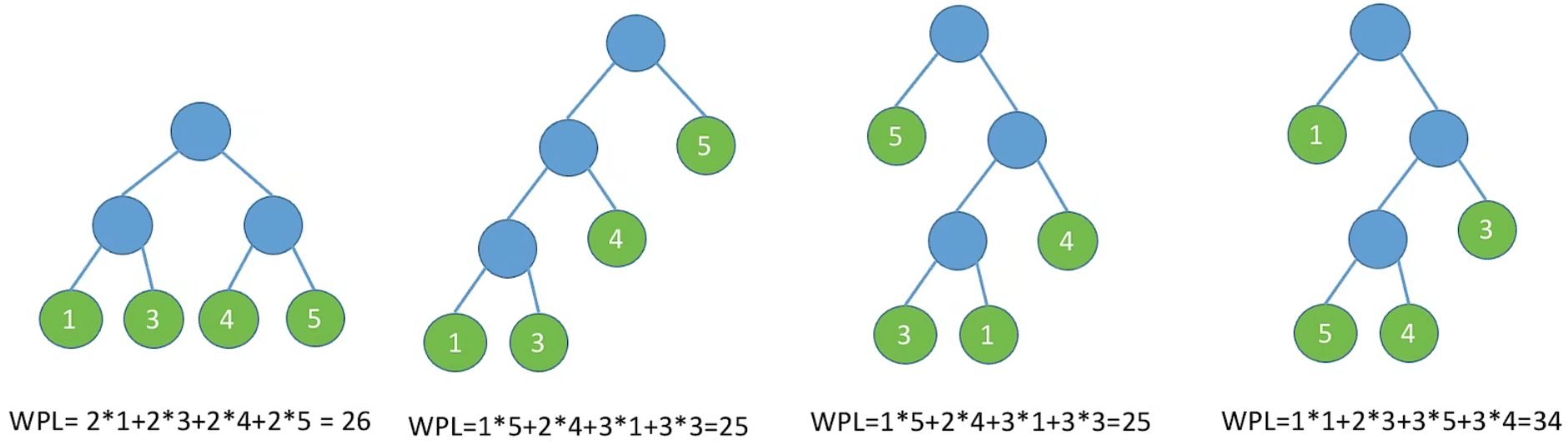
　　3、树的带权路径长度：

　　树中所有叶结点的带权路径长度之和

　　

　　12.2 哈夫曼树的定义

　　

　　在含有 n 个带权叶结点的二叉树中，其中带权路径长度 (WPL) 最小的二叉树称为哈夫曼树，也称最优二叉树

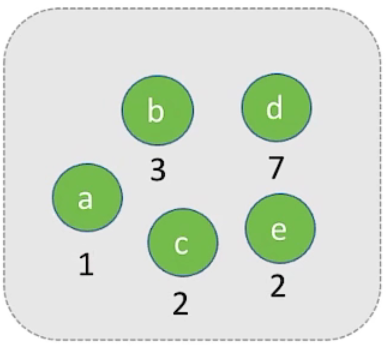
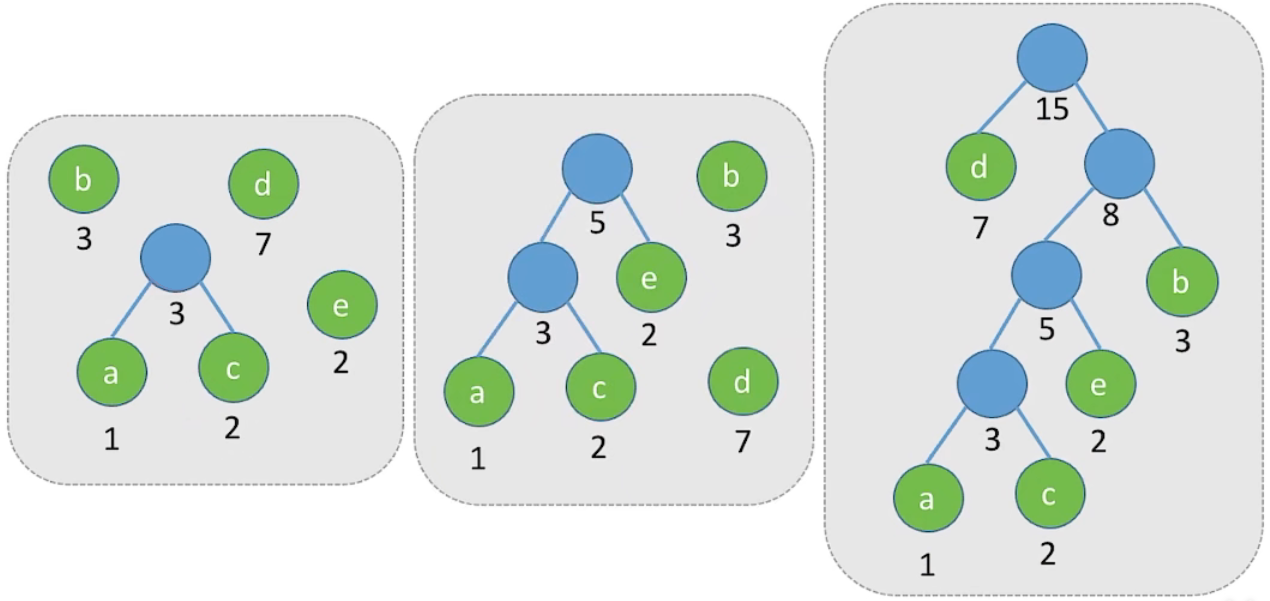
　　12.3 哈夫曼树的构造

　　1、给定 n 个权值分别为 , …. 的结点，构造哈夫曼树的算法描述如下：

　　(1) 将这 n 个结点分别作为 n 棵仅含一个结点的二叉树，构成森林 F

　　(2) 构造一个新结点，从 F 中选取两棵根结点权值最小的树作为新结点的左、右子树，并且将新结点的权值置为左、右子树上根结点的权值之和

　　(3) 从 F 中删除刚才选出的两棵树，同时将新得到的树加入 F 中

　　(4) 重复步骤 (2) 和 (3)，直至 F 中只剩下一棵树为止

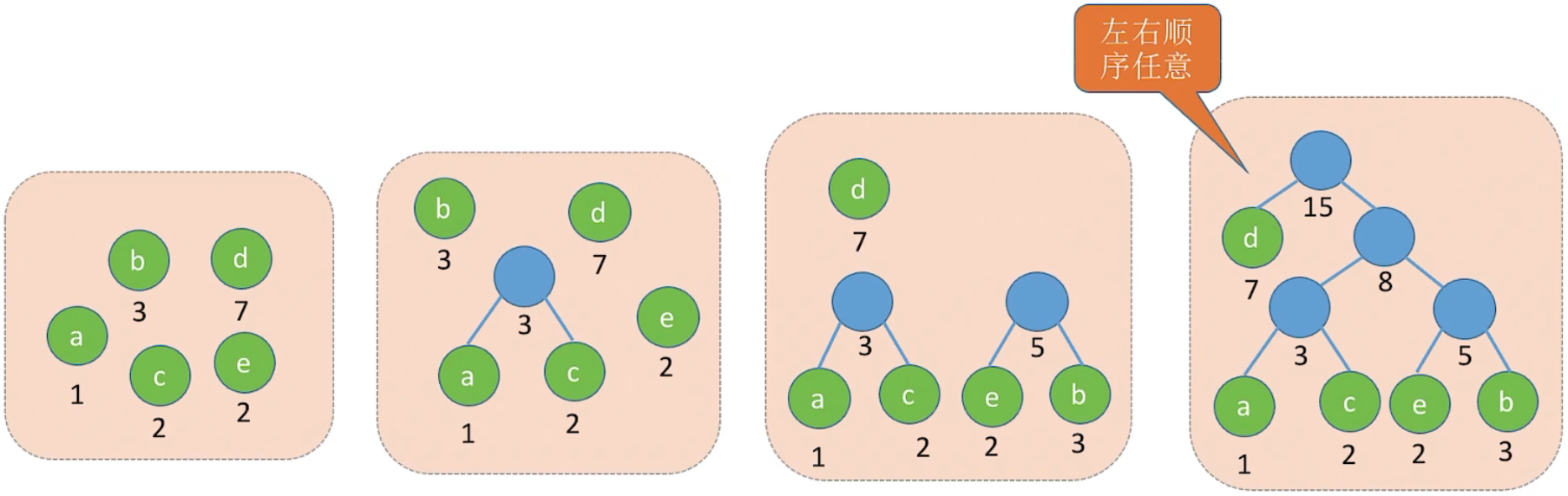
　　2、规律

　　(1) 每个初始结点最终都成为叶结点，且权值越小的结点到根结点的路径长度越大

　　(2) 哈夫曼树的结点总数为 2n-1

　　(3) 哈夫曼树中不存在度为1的结点

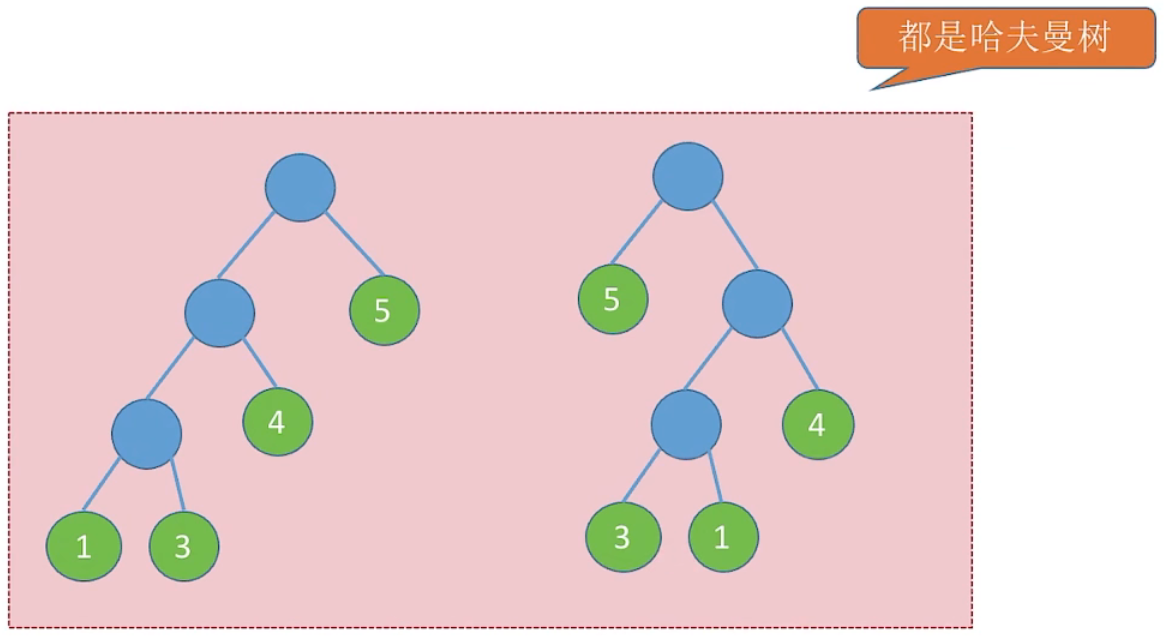
　　(4) 哈夫曼树并不唯一，但 WPL 必然相同且为最优

　　12.4 哈夫曼编码

　　1、电报

　　点、划 两个信号（二进制 0 / 1）

　　2、固定长度编码

　　每个字符用相等长度的二进制位表示

　　3、可变长度编码

　　允许对不同字符用不等长的二进制位表示

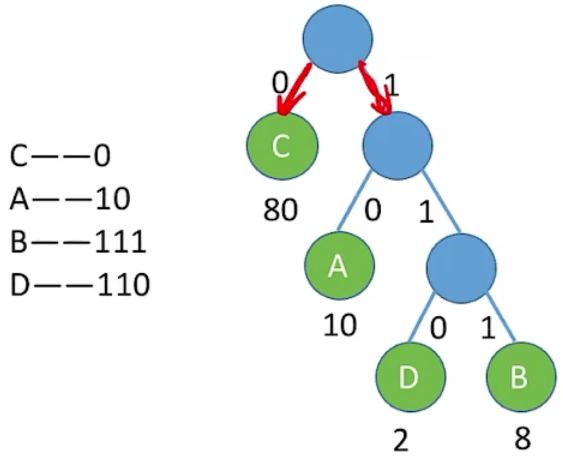
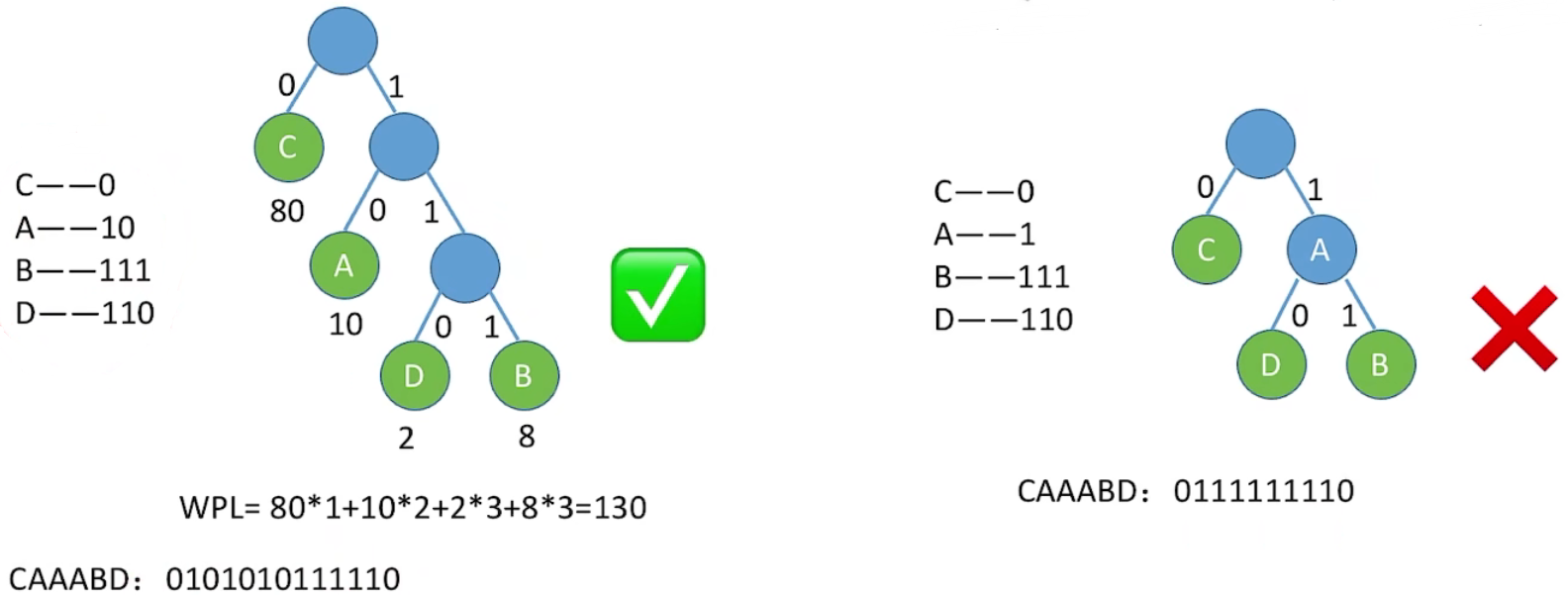
　　WPL = 80 * 1 + 10 * 2 + 2 * 3 + 8 * 3 = 130

　　4、注意：

　　若没有一个编码是另一个编码的前缀，则称这样的编码为前缀编码

　　5、哈夫曼编码

　　有哈夫曼树得到哈夫曼编码 —— 字符集中的每个字符作为一个叶子结点，各个字符出现的频度作为结点

　　的权值，根据之前介绍的方法构造哈夫曼树

　　12.5 例题

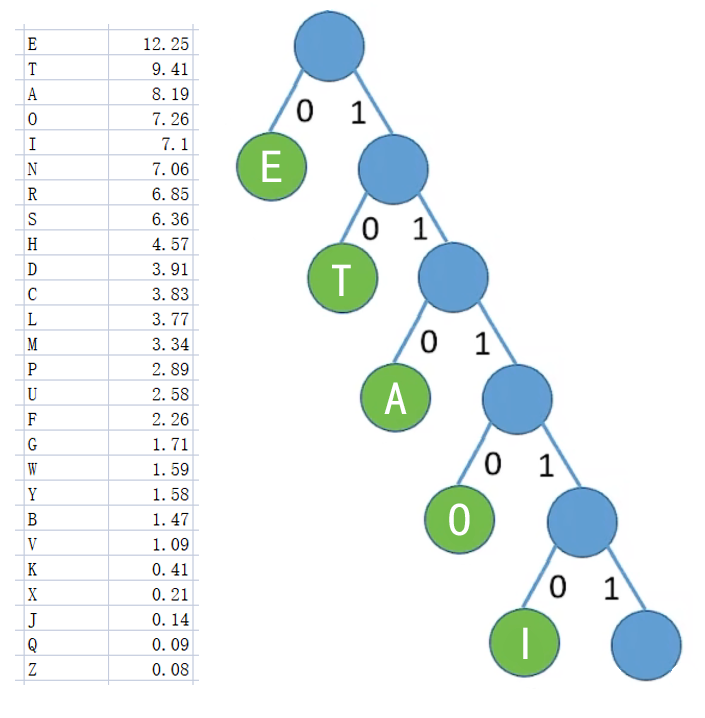
　　根据英文字母频次表设计哈夫曼编码

　　E 0；T 10；A 110；O 1110；I 11110；……

　　参考文献：

　　【1】视频：王道计算机考研 数据结构