二叉排序树查找不成功的asl_二叉排序树查找不成功的平均查找长度

2.PTA题目介绍（0–5分）
　　| 这个作业属于哪个班级 | 数据结构–网络2011/2012 |

　　| —- | —- | —- |

　　| 这个作业的地址 | DS博客作业05–查找 |

　　| 这个作业的目标 | 学习查找的相关结构 |

　　| 姓名 | 付峻霖 |

　　0.PTA得分截图

　　

　　1.本周学习总结（0-5分）

　　1.1 查找的性能指标

　　ASL（Average Search Length）

　　在查找运算中，由于所费时间在关键字的比较上，所以把平均需要和待查找值比较的关键字次数称为平均查找长度。

公式：ASL=∑ni=1pici
ASL是平均查找次数，在期末考中就考了一题哈希表，可以计算查找成功和查找不成功的平均查找长度，ASL可以很直观的计算出查找的效率

　　1.2 静态查找

　　1.2.1 顺序查找

　　顺序查找定义

　　就从头遍历到尾部一个一个找，找到待查找元素即查找成功，若到尾部没有找到，说明查找失败

顺序表的结构体定义

　　代码实现

　　ASL分析

　　成功：从头查找到尾，因此平均查找次数为(1+2+3..+n)/n=(n+1)/2

　　不成功：从头找到尾都没有找到，因此查找次数就为表的长度n

　　1.2.2 二分查找

　　要求是顺序表，根据顺序表构建二叉树，中间数为根，左小右大，也就是判定树
例如

　　

　　如图，根据判定树求解，假设每个元素的查找概率相等，则查找成功时的ASL=（11+22+43+44）/11。第一层的一个数比较成功时所需比较次数一次，第二层的两个数需要两次，依此类推。即查找成功时比较次数：为该结点在判定树上的层次数，不超过树的深度d=log2n+1， 查找不成功的过程就是走了一条从根结点到外部结点的路径d或d-1。
时间复杂度

　　每次查找后，范围缩小一半，因此时间复杂度为O(logn)
ASL分析

　　成功=每一层节点数层次数的总和/总结点数

　　不成功=其他不存在于树中的每一层节点数（层次数-1）/总结点数

　　1.3 二叉搜索树

　　二叉排序树的定义：

　　1.或者是空树

　　2.或者是满足以下性质的二叉树

　　★若它的左子树不空，则左子树上的所有关键字的值均小于根关键字的值

　　★若它的右子树不空，则右子树上的所有关键字的值均大于根关键字的值

　　1.3.1 如何构建二叉搜索树（操作）

　　结合一组数据介绍构建过程

　　设有一个输入数据的序列是 { 46, 25, 78, 62, 12, 80 }, 试画出从空树起，逐个输入各个数据而生成的二叉搜索树。

　　
二叉搜索树的ASL成功和不成功的计算方法。

　　★ASL成功=每个结点的高度相加/结点总数

　　例如：

　　☆ 5，4，3，2，1 五个关键字

　　

　　ASL=(1+2+3+4+5)/5=3

　　☆ 3，4，5，2，1关键字

　　

　　ASL=(1+2+2+3+3)/5=2.2

　　★ASL不成功=其他不存在于树中的每一层节点数（层次数-1）/总结点数

　　例如：

　　

　　1.3.2 如何构建二叉搜索树（代码）

　　结构体定义

　　二叉搜索树的构建操作

　　二叉搜索树的插入操作

　　二叉搜索树的删除操作

　　分析代码的时间复杂度

　　时间复杂度：最好：O(logn)，最坏：O(n)
为什么要用递归实现插入、删除？递归优势体现在代码哪里？

　　1.递归可以使算法大大简化，代码足够精简(意味着不好理解)

　　2.保留父子关系，便于删除和插入顺利找到父亲和孩子

　　1.4 AVL树

　　1.AVL树解决什么问题，其特点是什么？

　　★AVL能解决二叉搜索树存在数据分配不平衡的问题，她将二叉搜索树调整为经可能的矮，这样平均查找长度越小，查找速度越快。

　　★平衡二叉树是二叉排序树的改进版，也就是说平衡二叉树是二叉排序树的一个特殊情况

　　★我们将每个结点的平衡因子的绝对值都不超过1的二叉排序树称为平衡二叉树

　　★平衡因子：左子树高度-右子树高度

　　2.结合一组数组，介绍AVL树的4种调整做法。

　　输入关键字序列{16,3,7,11,9,26,18,14,15}，构造一颗AVL树。 有调整要写成调整类型及结果

　　

　　no picture you say a J8，4种调整做法图中已经画的非常清楚了，我这就不再进行过多的文字赘述

　　3.AVL树的高度和树的总节点数n的关系？

　　高度为 h 的 AVL 树，最多为满二叉树，节点数 N 最多2^h − 1； 最少类似于斐波那契数列，满足N(h)=N(h− 1) +N(h− 2) + 1 的计算公式

　　4.介绍基于AVL树结构实现的STL容器map的特点、用法。

　　Map是STL的一个关联容器，翻译为映射，数组也是一种映射。如：int a[10] 是int 到 int的映射，而a[5]=25,是把5映射到25。数组总是将int类型映射到其他类型。这带来一个问题，有时候希望把string映射成一个int ，数组就不方便了，这时就可以使用map。map可以将任何基本类型（包括STL容器）映射到任何基本类型（包括STL容器）。

　　★可调用函数

　　begin() 返回指向map头部的迭代器

　　end() 返回指向map末尾的迭代器

　　rbegin() 返回一个指向map尾部的逆向迭代器

　　rend() 返回一个指向map头部的逆向迭代器

　　lower_bound() 返回键值>=给定元素的第一个位置

　　upper_bound() 返回键值>给定元素的第一个位置

　　empty() 如果map为空则返回true

　　max_size() 返回可以容纳的最大元素个数

　　size() 返回map中元素的个数

　　clear(） 删除所有元素

　　count() 返回指定元素出现的次数

　　equal_range() 返回特殊条目的迭代器对

　　erase() 删除一个元素

　　swap() 交换两个map

　　find() 查找一个元素

　　get_allocator() 返回map的配置器

　　insert() 插入元素

　　key_comp() 返回比较元素key的函数

　　value_comp() 返回比较元素value的函数

　　1.5 B-树和B+树

　　1.5.1 B-树和AVL树区别，其要解决什么问题？

　　★AVL树结点仅能存放一个关键字，树的高度较高，而B-树的一个结点可以存放多个关键字，降低了树的高度，可以解决大数据下的查找

　　1.5.2 B-树定义。结合数据介绍B-树的插入、删除的操作，尤其是节点的合并、分裂的情况

　　B-树定义

　　也叫B树，即平衡多路查找树，m阶B树表示节点可拥有的最多m个孩子，2-3树是3阶B树，2-3-4树是4阶B树。多叉树可以有效降低树的高度，h=log_m(n)，m为log的底数。

　　★一颗m阶的B树需要满足下列条件：

　　①每个结点最多有m-1个关键字。

　　②根结点最少可以只有1个关键字。

　　③非根结点至少有m/2-1个关键字。

　　④每个结点中的关键字都按照从小到大的顺序排列，每个关键字的左子树中的所有关键字都小于它，而右子树中的所有关键字都大于它。

　　⑤所有叶子结点都位于同一层，或者说根结点到每个叶子结点的长度都相同。

B-树的插入

　　★思路：插入的时候，我们需要记住一个规则：判断当前结点key的个数是否小于等于m-1，如果满足，直接插入即可，如果不满足，将节点的中间的key将这个节点分为左右两部分，中间的节点放到父节点中即可。

　　★举例：在5阶B树中，结点最多有4个key,最少有2个key（注意：下面的节点统一用一个节点表示key和value）。

　　插入18，70，50,40

　　

　　插入22

　　

　　插入22时，发现这个节点的关键字已经大于4了，所以需要进行分裂

　　分裂后结果如下

　　

　　接着再分别插入23，25，39

　　

　　分裂后，得到最终结果

　　

B-树的删除

　　★思路：在B-树中删除节点时，可能会发生向兄弟节点借元素，和孩子节点交换元素，甚至节点合并的过程。

　　★举例：我们以下面的5阶树为基础，每个节点内元素个数为2~4个，依次删除8、16、15、4这4个元素。

　　

　　删除8，因为删除8后，不破坏树的性质，所以直接删除即可。

　　

　　然后删除16，这导致该节点只剩下一个13节点，不满足节点内元素个数为2~4个的要求了。所以需要调整。这里可以向孩子借节点，把17提升上来即可，得到下图。这里不能和兄弟节点借节点，因为从3，6节点中把6借走后，剩下的3也不满要求了。另外，也不能把孩子中的15提升上来，那样会导致剩下的14不满足要求。

　　

　　然后删除15，删除15后同样需要调整。调整的方式是，18上升，17下降到原来15的位置，得到下图。

　　

　　然后删除元素4，删除4后该节点只剩下5，需要调整。可是它的兄弟节点也都没有多余的节点可借，所以需要进行节点合并。节点合并时，方式会有多种，我们选择其中的一种即可。这里，我们选择父节点中的3下沉，和1，2，以及5进行合并，如下图。

　　

　　这次调整后，导致6不符合要求了。另外，6非根节点，但只有2个孩子，也不符合要求。需要继续调整。调整的方式是，将10下沉，和6，以及13，18合并为根节点

　　调整完后得到最终结果

　　

　　1.5.3 B+树定义，其要解决问题

　　B+树定义

　　B+树是应数据库所需而出现的一种 B 树的变形树。

　　★一棵m阶的B+树需要满足下列条件：

　　①每个分支结点最多有m棵子树（子结点）

　　②非叶根结点至少有两棵子树，其他每个分支结点至少有m/2棵子树

　　③结点的子树个数与关键字个数相等

　　④所有叶结点包含全部关键字及指向相应记录的指针，而且叶结点中将关键字按大小顺序排列，并且相邻叶结点按大小顺序相互链接起来。

　　⑤所有分支结点（可看成是索引的索引）中仅包含它的各个子结点（即下一级的索引块）中关键字的最大值及指向其子结点的指针

解决的问题

　　①B树只适合随机检索，B+树同时支持随机检索和顺序检索，因此B+树比B树更适合实际应用中操作系统的文件索引和数据库索引 **

　　②数据库索引要采用B+树，因为B+树的叶子节点使用指针顺序连接在一起，只要遍历叶子节点就可以实现整棵树的遍历。而且在数据库中基于范围的查询是非常频繁的，而B树效率太低**。

　　1.6 散列查找。

　　1.6.1 哈希表的设计主要涉及哪几个内容？

　　定义

　　哈希表又叫散列表，是根据关键码值(Key value)而直接进行访问的数据结构。也就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做散列函数，存放记录的数组叫做散列表。

哈希函数常用构造方法

直接定址法

　　直接定址法是以关键字k本身加上某个常数c作为哈希地址的方法。

　　哈希函数为h(k)=k+c

　　该方法的特点是哈希函数计算简单，若关键字分布不连续将造成内存单元大量浪费。
除留取余法

　　除留余数法是用关键字k除以某个不大于哈希表长度m的整数p所得的余数作为哈希地址。

　　哈希函数为h(k)=k mod p

　　该方法选取的p最好为不大于m的素数，从而尽量减少发生哈希冲突的可能性。

　　1.6.2 结合数据介绍哈希表的构造及ASL成功、不成功的计算

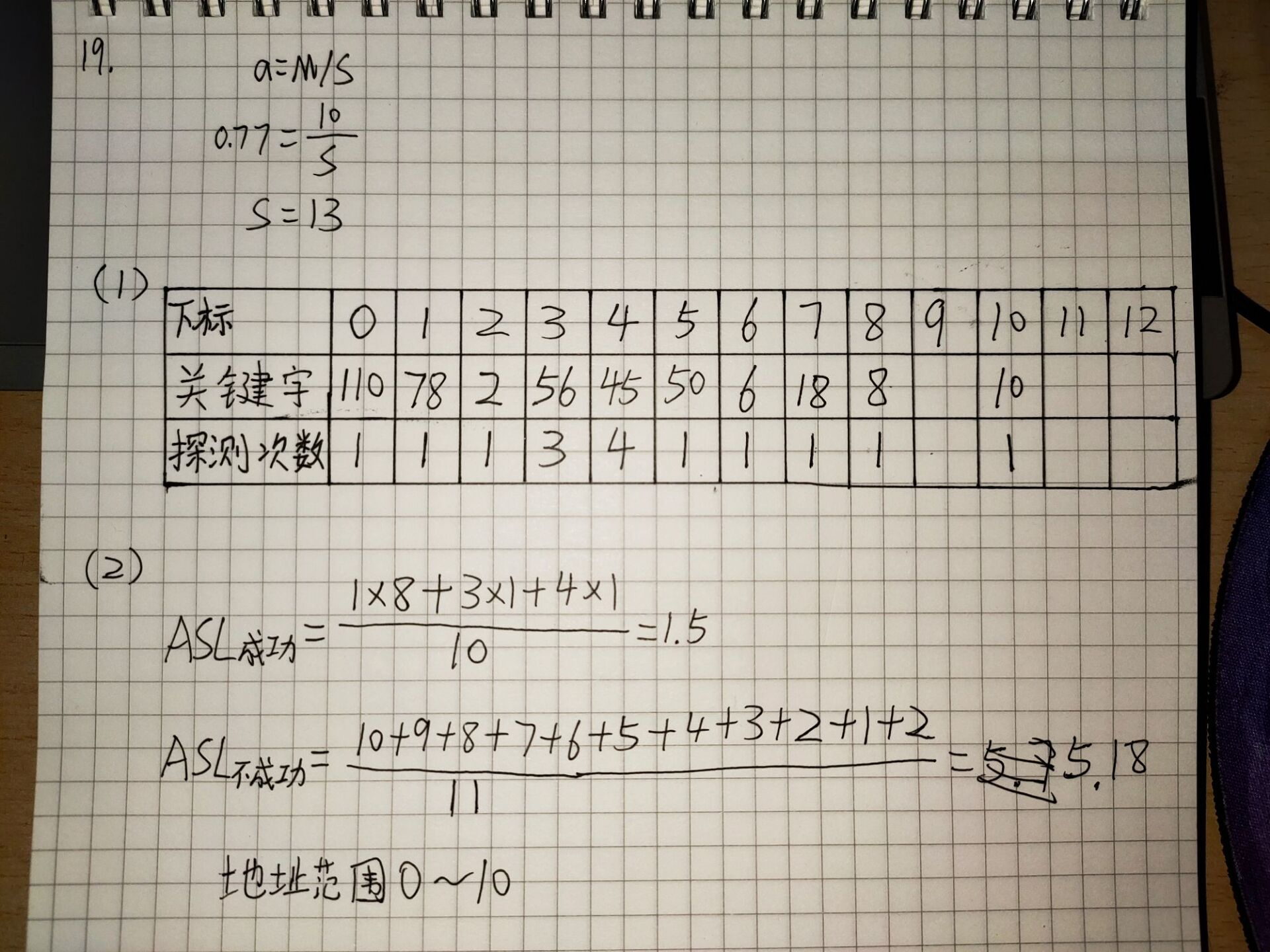
　　例如关键字序列{18,2,10,6,78,56,45,50,110,8}这样一组数据，散列函数为：H(key)=key)mod 11，处理冲突采用线性探测法，装填（载）因子为0.77。

　　首先根据装填因子求出散列表长度为13，画图后，对每个关键字取余11，把他们一个一个放到散列表中，如果有冲突，则采取线性探测法

　　

　　1.6.3 结合数据介绍哈希链的构造及ASL成功、不成功的计算

　　例如关键字序列(25，10，8，27，32，68)这样一组数据，散列表的长度为8，散列函数H(k)=k mod 7

　　用链地址法的好处是不会存在冲突的现象，当出现俩数据取余后的值相同时，则头插法插在同一条链上。

　　

　　2.PTA题目介绍（0–5分）

　　2.1 是否完全二叉搜索树（2分）

　　什么是完全二叉搜索树呢？

　　通俗点来讲，就是完全二叉树+二叉搜索树，需要同时满足这两种树的条件，所以要求

　　①生成结点的顺序是严格按照从上到下，从左往右的顺序来构建的二叉树。

　　②任意一个结点，左子树所有结点的键值要大于结点，右子树所有结点的键值要小于结点
判断一棵树是否是完全二叉树的基本思路

　　①如果树为空，则直接返回错

　　②如果树不为空：层序遍历二叉树

　　★如果一个结点左右孩子都不为空，则pop该节点，将其左右孩子入队列；

　　★如果遇到一个结点，左孩子为空，右孩子不为空，则该树一定不是完全二叉树；

　　★如果遇到一个结点，左孩子不为空，右孩子为空；或者左右孩子都为空；则该节点之后的队列中的结点都为叶子节点；该树才是完全二叉树，否则就不是完全二叉树；

　　

　　如图所示上面这种从上到下，从左到右依次构建二叉树，并且满足二叉搜索树的条件，这样的树就是完全二叉搜索树。

　　

　　而这种，就不是了，因为不满足完全二叉树的条件：从上到下，从左到右依次构建二叉树。

　　2.1.1 伪代码（贴代码，本题0分）

　　2.1.2 提交列表

　　

　　2.1.3 本题知识点

　　①用了层次遍历，因此要借用了队列来存储树中的结点

　　②调用了队列的相关库函数，q.push()，q.front()，q.pop()等等

　　③关于完全二叉搜索树概念的理解：完全＋搜索

　　2.2 航空公司VIP客户查询（2分）

　　2.2.1 伪代码（贴代码，本题0分）

　　2.2.2 提交列表

　　

　　2.2.3 本题知识点

　　①哈希表的运用。利用哈希表来存放结点所在下标。

　　②调用了图的库函数，用M.count(id)求数组M中下标为id的数据是否存在

　　③map<string,int>M

　　④调用max(a,b)函数来求a b中的较大值

　　2.3 基于词频的文件相似度（1分）

　　2.3.1 伪代码（贴代码，本题0分）

　　2.3.2 提交列表

　　

　　2.3.3 本题知识点

　　①调用了图的库函数

　　②利用getchar()吸收回车

　　③使用了迭代器