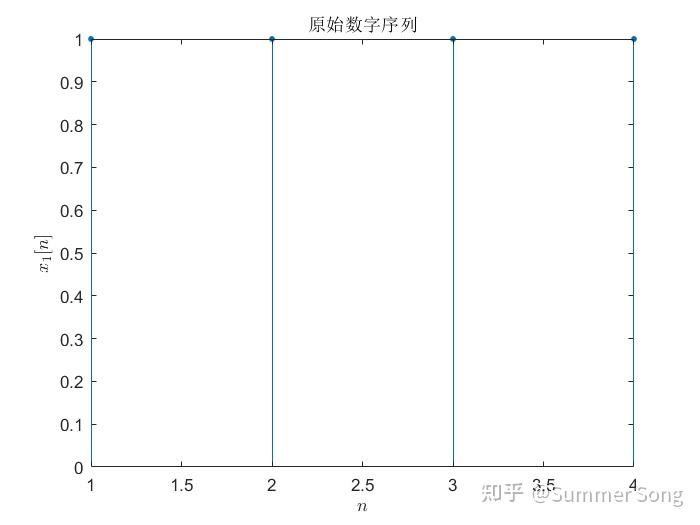
【数字信号处理实验】实验六 利用DFT计算数字信号频谱 本文代码已上传至github:MyShare/DSP Experiment/ex6 at master · TyroGzl/MyShare (github.com)如无法访问,也可以【G的科研生活】,sigusoft【DSPEX】 一、实验目的 掌握数字信号频谱分析方法掌握DFT与DTFT的频谱关系掌握DFT原理及软件编程实现方法掌握补零运算对DFT结果的影响 二、实验过程与结果 1. 数字信号的DFT计算 (1)DFT函数的编写 按照DFT定义式编写计算
![matlab用fft画图像频谱图_MATLAB fft插图3 x_1 [n]=R_4 [n]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)

![matlab用fft画图像频谱图_MATLAB fft插图7 x_1 [n]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)


![matlab用fft画图像频谱图_MATLAB fft插图7 x_1 [n]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)


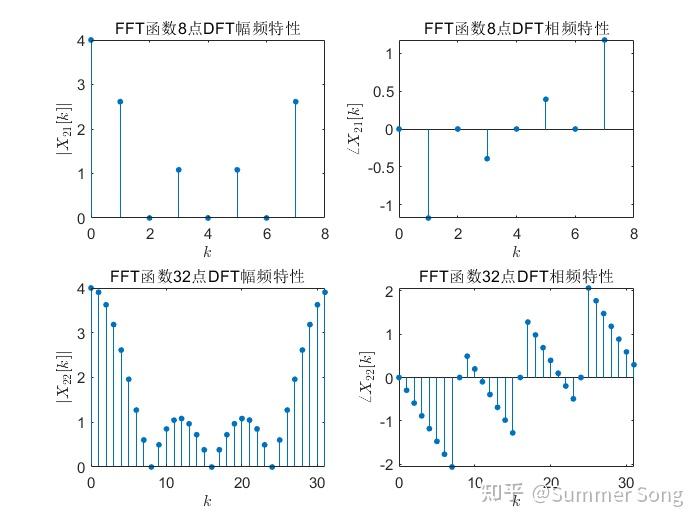
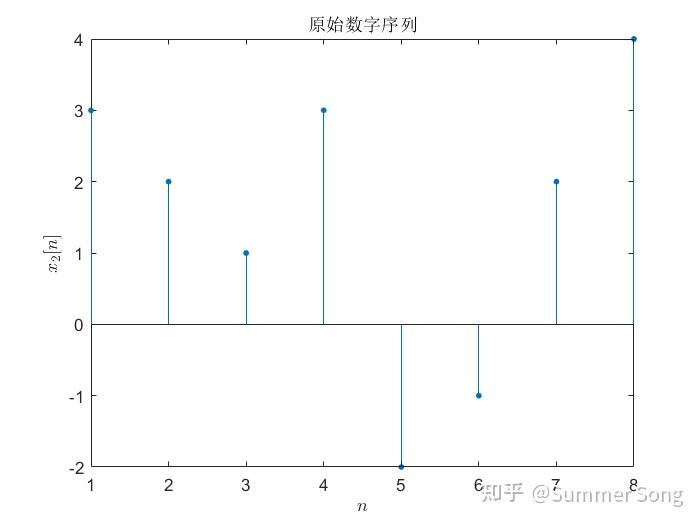
![matlab用fft画图像频谱图_MATLAB fft插图17 x_2 [n]=[3,2,1,3,-2,-1,2,4]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png) 。选取变换点数
。选取变换点数 ,调用MATLAB中的函数计算序列
,调用MATLAB中的函数计算序列![matlab用fft画图像频谱图_MATLAB fft插图21 x_2 [n]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)

![matlab用fft画图像频谱图_MATLAB fft插图21 x_2 [n]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)



![matlab用fft画图像频谱图_MATLAB fft插图21 x_2 [n]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)



![matlab用fft画图像频谱图_MATLAB fft插图33 [0,2]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![matlab用fft画图像频谱图_MATLAB fft插图3 x_1 [n]=R_4 [n]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)


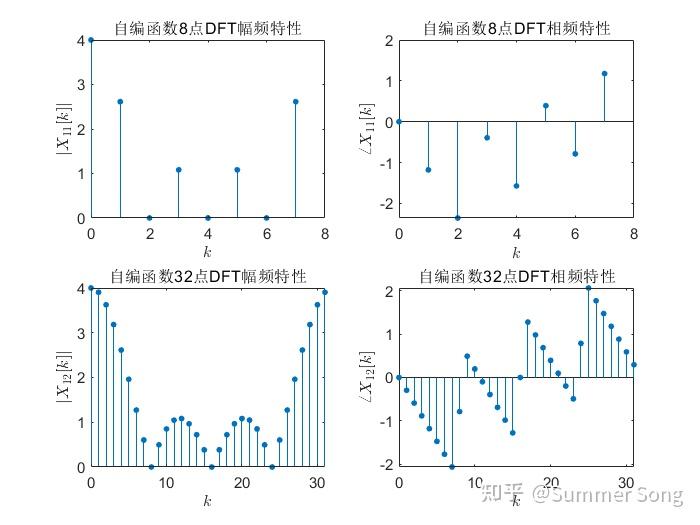
![matlab用fft画图像频谱图_MATLAB fft插图21 x_2 [n]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
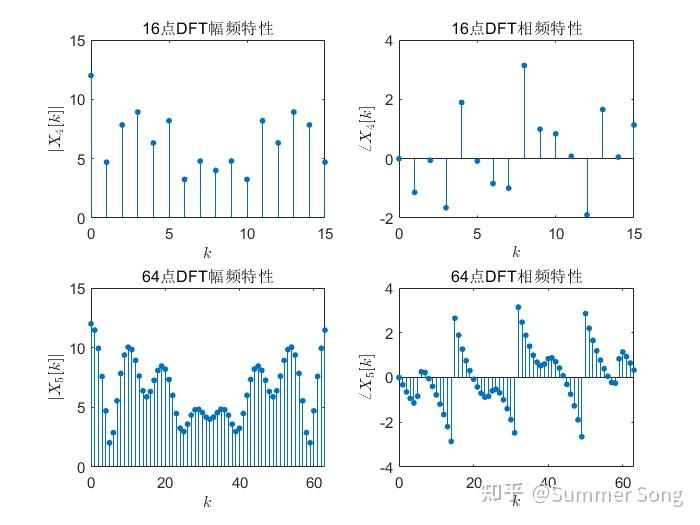
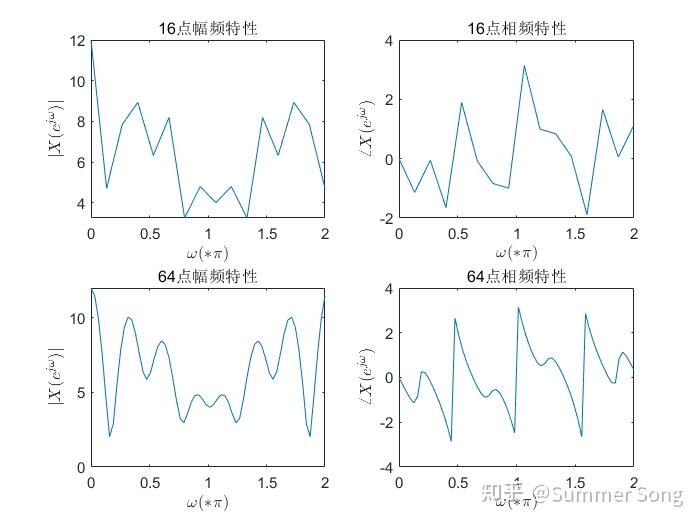
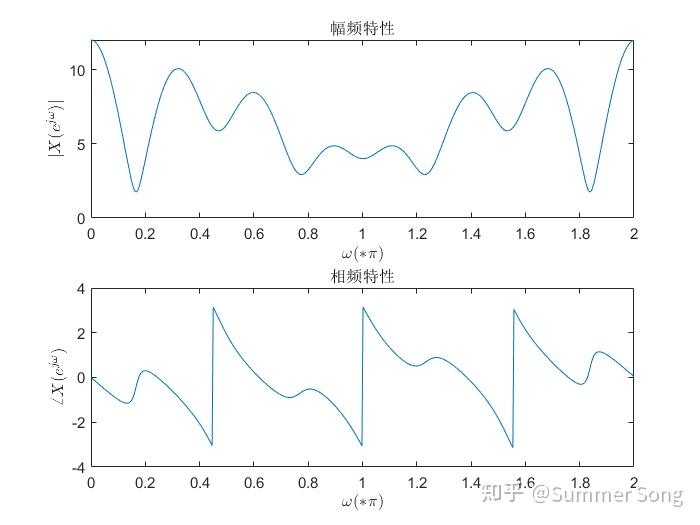
![matlab用fft画图像频谱图_MATLAB fft插图65 [0,2π]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)

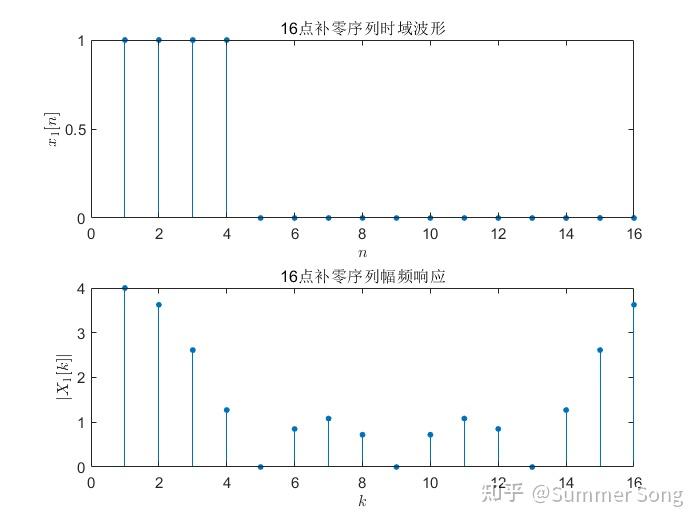
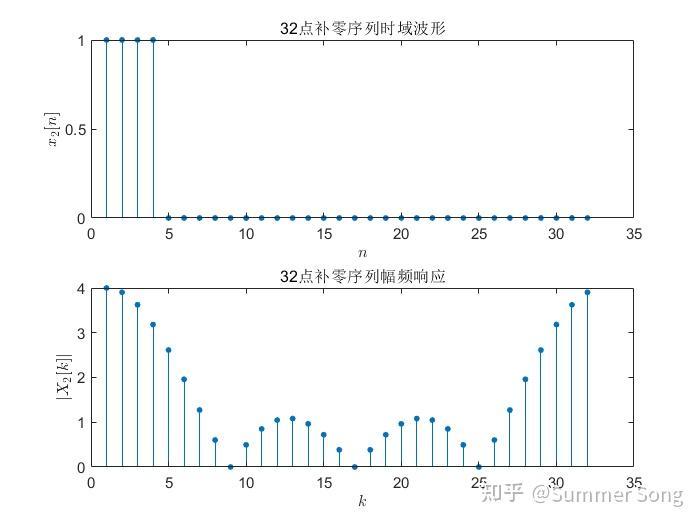
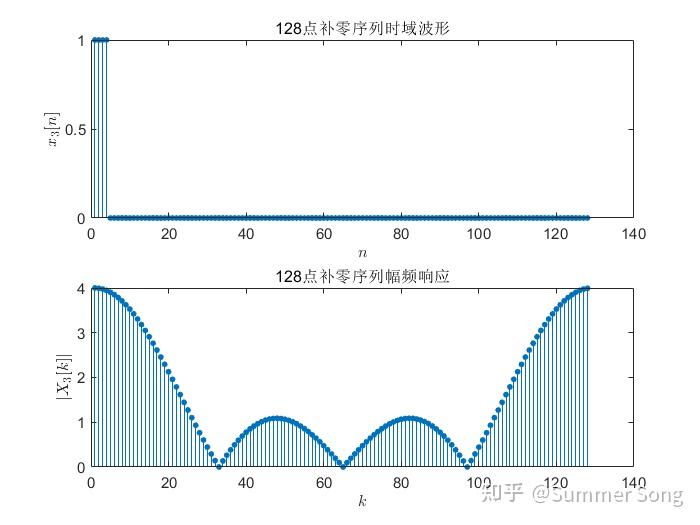
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/79895.html