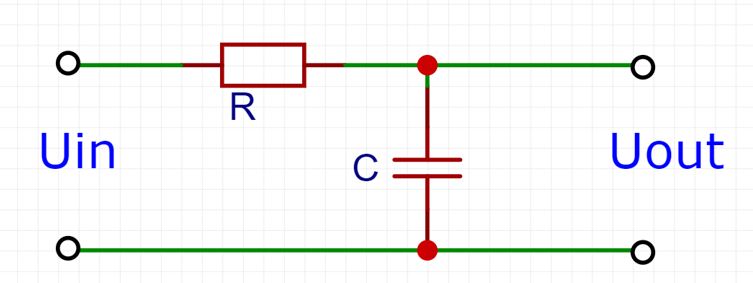
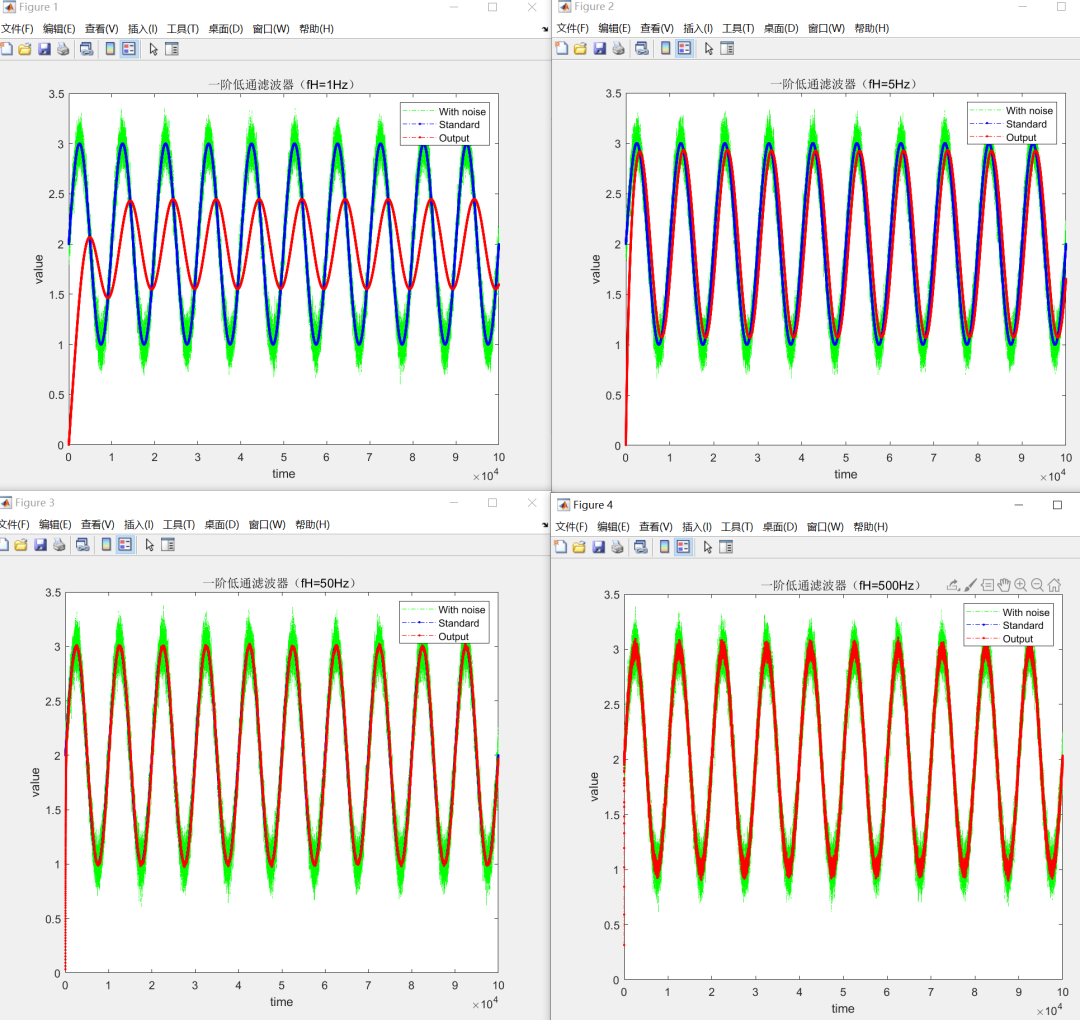
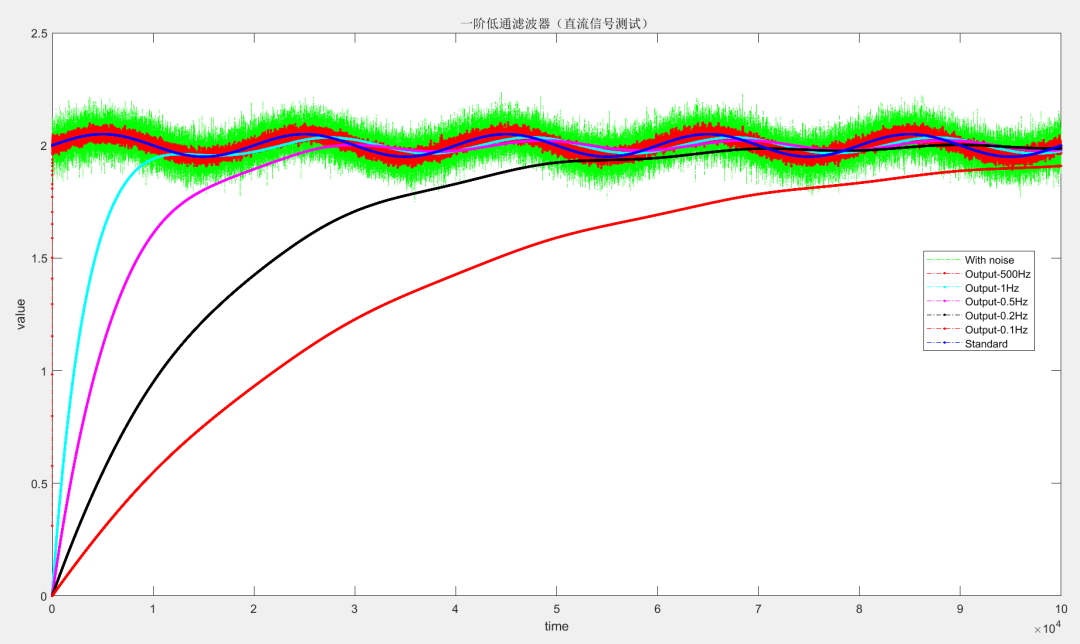
一阶数字低通滤波器原理及公式推导 前面我们基本把有感FOC介绍得差不多了，接下来我本打算进入无感FOC控制的深入学习，奈何导师项目项目太多太杂……………………先把自己这段时间学的东西总结分享一下再说吧。查阅了很多无感FOC控制的相关资料，把基本原理和流程渐渐的了解了一下（以后有时间再详细介绍了），发现很多环节都会用到”一阶低通数字滤波器“（相电流滤波，反电势滤波，角度、转速滤波，校正因子滤波），虽然代码里面只是一个简单的公式，但为了控制系统的参数设计，我还是浅浅的去探究了一下其基本原理，如有错误还望提出指正。 开局先直接给出公式：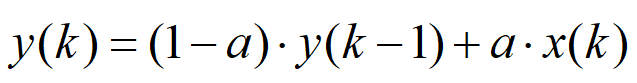 
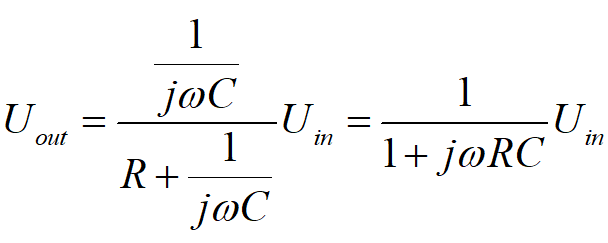
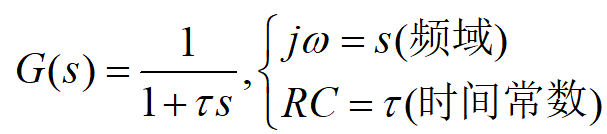
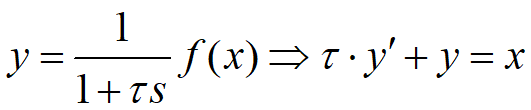
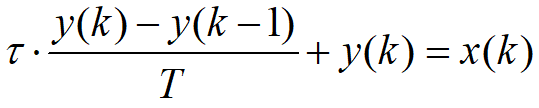
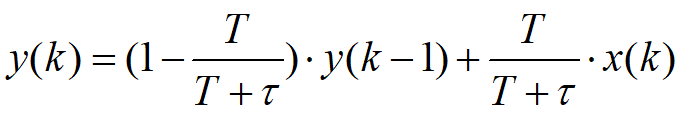
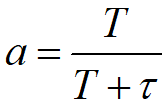
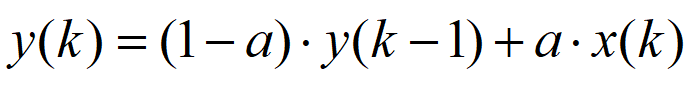
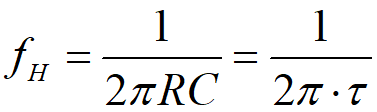
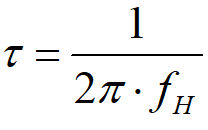
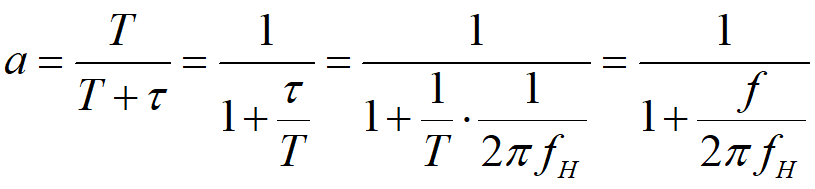
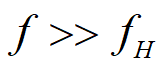
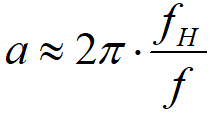
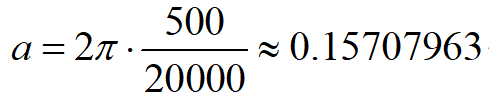
式中：x(k)为当前输入，y(k-1)为上一次的输出，y(k)为当前计算的输出；a为滤波系数，取值范围0~1，a取值越小，当前输入权重就越小，输出波形越平滑，但响应灵敏度降低； 如果只是套用公式写代码的话，看到这里就可以结束了，想要理解其中的原理，以及采样频率、截止频率和参数的计算，那么请接着往下看。 01. 原理及公式推导 ”一阶低通数字滤波器“对应的物理电路模型是”一阶RC低通滤波电路“，电路如下图所示。 
电容的阻抗表示为1/jωC，对于上面电路，有输入输出电压关系： 
上式写成传递函数形式： 
， 在《自动控制原理》中称为一阶惯性环节。 由Y(s)=G(s).F(s)得到时域的微分方程： 
使用一阶后向差分法，对上面微分方程进行离散化，有： 
其中T为采样周期，对上式进行整理化简可写成： 
令
得到一般表达式：
，a称为滤波系数。 02. 截止频率和参数计算 对于电路模型，有截止频率
（截止频率定义为幅频响应曲线衰减 -3db，即为原来的1/sqrt(2)时的频率，模电里面的基础知识这里不细讲） 可得是将常数
代入滤波系数a的表达式得： 
式中f=1/T为采样频率。 在实际的应用中，一般有采样频率远大于截止频率，即有
，故近似有
，所以已知截止频率和采样频率，我么就能够计算滤波系数a的值了。 又会问：截止频率和采样频率怎么确定呢？选取不同的值会对计算输出有什么影响呢？下面为你简单介绍一下。 03. 频率的选择 3.1采样频率的选择 一般人为主观选择，在不影响其他功能性能的条件下，尽量越大越好。 先以我之前做的电机控制为例。在程序中，PWM定时器开启中断，在中断服务函数中用ADC采集相电流，故采样频率就等于PWM定时器频率，我在控制代码中用的是20kHz，即采样频率f=20kHz。 3.2截止频率的选择 根据采样对象信号的频率选择，一般稍大于被采样信号的最大基波频率就好。 还是以我做的电机控制为例。我用的永磁同步电机额定转速为3000rpm，极对数为4，采样对象为相电流。则在额定条件下，相电流的频率为f_current=3000*4/60=200Hz，考虑到电机超负荷运行，瞬时转速可以大于3000，保留一定余量，我取截止频率f_H=500Hz。如此计算得滤波系数
。 在电机运行前，对放大器进行校准时，只考虑直流偏置输入，即被采样的信号频率趋近于0Hz，主要滤掉电路中的高频干扰和噪声，故可把截止频率取得很小，我这里取f_H=5Hz，计算得滤波系数a=0.00157。 04频率选择对输出的影响（附仿真分析） 在采样频率固定的情况下，截止频率越大，滤波系数a的值越大，当前输入的权重就越大，计算的输出和实际的输出跟踪效果更好，即动态响应更好，幅值衰减的影响更小。 减小截止频率，滤波系数a的值越小，当前输入的权重越小，故计算的输出信号更平滑，对噪声干扰和谐波的滤除效果更好，但是动态响应变差，而且会产生一定程度的幅值衰减。 下面是matlab代码和仿真结果分析： 仿真结果： 
图中，绿色为含有噪声的采样信号，蓝色为标准的正弦信号，红色为采样信号经过一阶低通滤波器的计算输出。 可以发现，当截止频率较小时，输出信号幅值衰减明显，且存在一定滞后；随着截止频率的增大，对标准正弦信号的跟踪效果越好；当截止频率过大时，几乎能完全复现采样信号，但是对噪声的滤波效果变差。 下面再看一下对直流信号的测试 
可以看出，随着截止频率的减小，计算输出的信号越来越平滑，接近直流信号，但同时调节时间也增大，对应我前面电机控制中，对放大器的校准时间需要延长。在实际应用中，对于直流信号的滤波，截止频率一般取1~50Hz我觉得就好了（当然也有可能其它情况我没想到）。 最后附上matlab的仿真源代码 代码源程序： 交流信号部分： 直流信号部分： 审核编辑：汤梓红
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/79558.html
