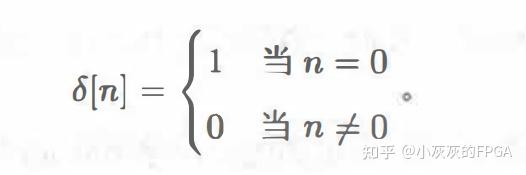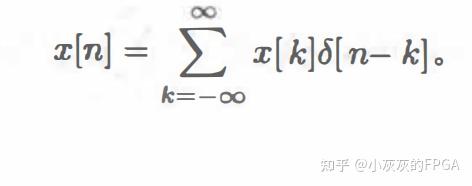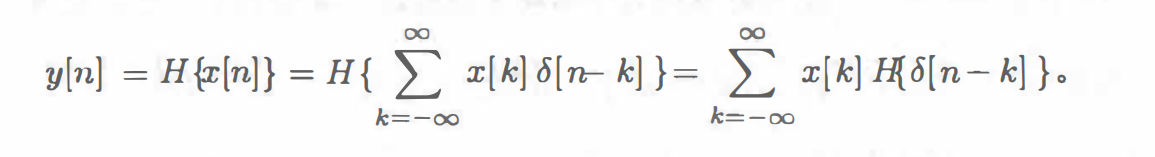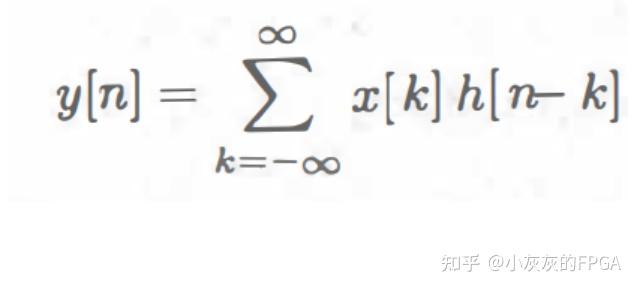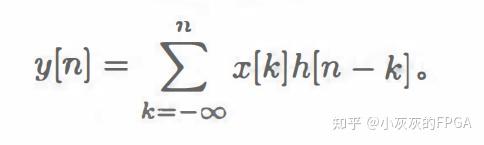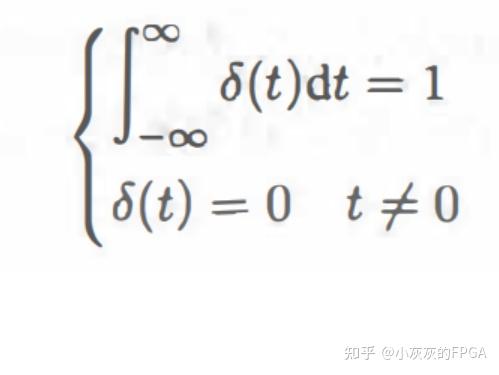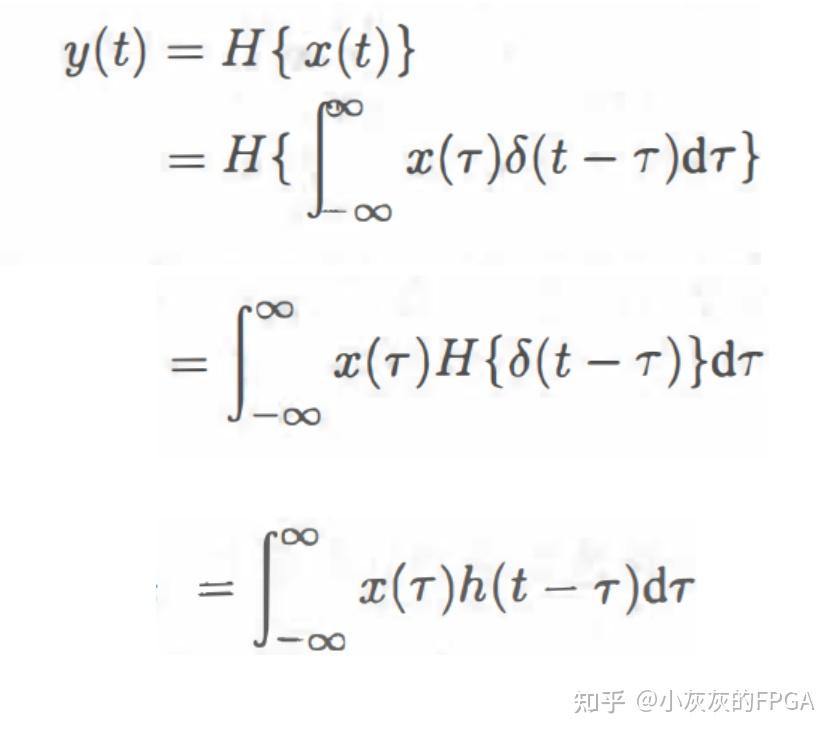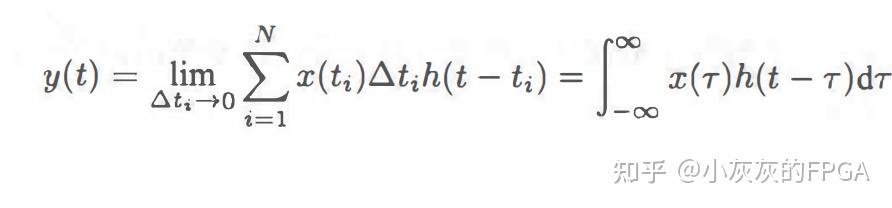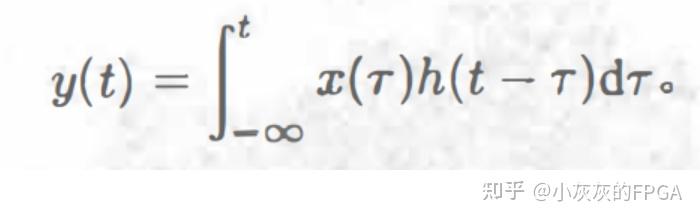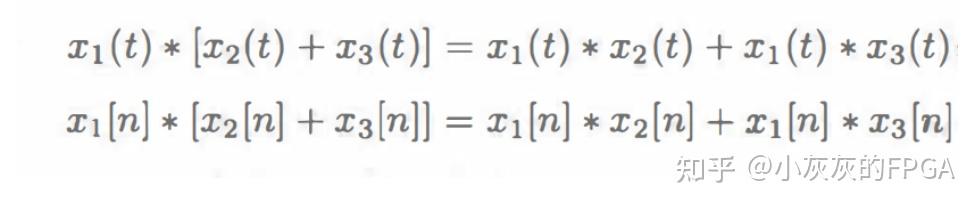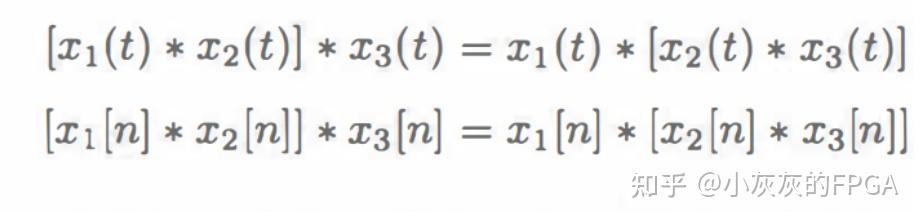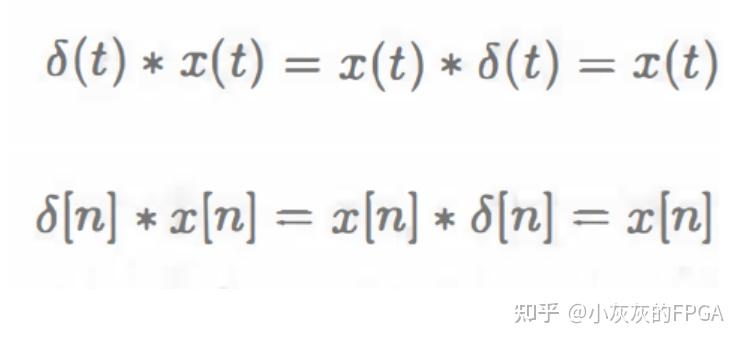matlab 数组移位_matlab 左移如何通俗易懂地解释卷积?我们做个小学乘法:用一个 去和 相乘, 得到的结果是 ,前者它的系数分别为 和 ,结果项的系数分别是 , 这个结果是和卷积严格对应的.因为在做多项式相乘时,我们会用其中一个式子,对另一个式子的系数逐个相乘并并相
如何通俗易懂地解释卷积? 我们做个小学乘法: 用一个
 去和
去和
 相乘, 得到的结果是
相乘, 得到的结果是
 , 前者它的系数分别为
, 前者它的系数分别为
![matlab 数组移位_matlab 左移插图7 [1,1]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 和
和
![matlab 数组移位_matlab 左移插图9 [1,2]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) ,结果项的系数分别是
,结果项的系数分别是
![matlab 数组移位_matlab 左移插图11 [1,3,2]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) , 这个结果是和卷积严格对应的. 因为在做多项式相乘时,我们会用其中一个式子,对另一个式子的系数逐个相乘并并相加。在合并同类型时,其实就是不同维度上(二次、三次、四次、五次项等)进行加和。 所以实际上, 多项式的相乘就是离散卷积啦. 民科一点的说, 卷积就是多项式之间的乘法。之所以叫卷, 而”卷”就是拿着一个多项式去反复作用。 与卷积稍有不同的是互相关运算, 在神经网络里约定俗地称为卷积. 它是用来衡量相似程度的. x1和x2多大程度上相似? 当然是相乘结果为平方的时候. 二维卷积就是把一维卷积后的数字再作一次纵向的卷积. 反正我觉得这是最快最通俗易懂的方式了. 为什么系统的输入与输出之间有一个卷积的关系? 卷积实际上只是在说一件事:输入与输出之间并不是一一对应的关系。某一时刻的输出g(t)与此前多个时刻的输入f(t)都有关系。即 g(t)=f(t)*h(t),h(t)代表权重系数。 看看我的这篇文章吧,应该会对你有所帮助,我,这一系列文章都可以学习本节目录 本节内容 一、线性系统的激励响应 输入信号又称为激励,输出信号又称为响应。一个信号输入给一个线性系统的时候,输出信号会因输入信号不同而不同。 1、离散δ信号 离散δ信号,又称为离散冲激序列,公式可以表述为:
, 这个结果是和卷积严格对应的. 因为在做多项式相乘时,我们会用其中一个式子,对另一个式子的系数逐个相乘并并相加。在合并同类型时,其实就是不同维度上(二次、三次、四次、五次项等)进行加和。 所以实际上, 多项式的相乘就是离散卷积啦. 民科一点的说, 卷积就是多项式之间的乘法。之所以叫卷, 而”卷”就是拿着一个多项式去反复作用。 与卷积稍有不同的是互相关运算, 在神经网络里约定俗地称为卷积. 它是用来衡量相似程度的. x1和x2多大程度上相似? 当然是相乘结果为平方的时候. 二维卷积就是把一维卷积后的数字再作一次纵向的卷积. 反正我觉得这是最快最通俗易懂的方式了. 为什么系统的输入与输出之间有一个卷积的关系? 卷积实际上只是在说一件事:输入与输出之间并不是一一对应的关系。某一时刻的输出g(t)与此前多个时刻的输入f(t)都有关系。即 g(t)=f(t)*h(t),h(t)代表权重系数。 看看我的这篇文章吧,应该会对你有所帮助,我,这一系列文章都可以学习本节目录 本节内容 一、线性系统的激励响应 输入信号又称为激励,输出信号又称为响应。一个信号输入给一个线性系统的时候,输出信号会因输入信号不同而不同。 1、离散δ信号 离散δ信号,又称为离散冲激序列,公式可以表述为:

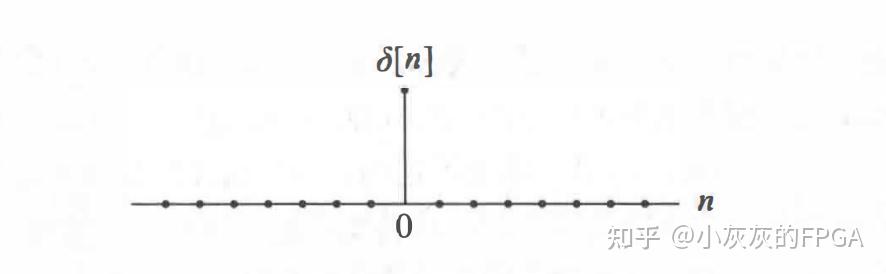
 离散冲激序列的图形可以表示为:
离散冲激序列的图形可以表示为:

 2、离散卷积 任何一个离散信号x[n]都可以表示称为如下的形式:
2、离散卷积 任何一个离散信号x[n]都可以表示称为如下的形式:

 在上式中,只有当k=n时,δ[n-k]=1,其余时刻均为零,求和之后为x[n]。 假设一个离散系统H{.}是一个线性系统,根据叠加性和数乘性可知:
在上式中,只有当k=n时,δ[n-k]=1,其余时刻均为零,求和之后为x[n]。 假设一个离散系统H{.}是一个线性系统,根据叠加性和数乘性可知:

 进一步可以得到:h[n-k]=H{δ[n-k]},从而带入上式中可得:
进一步可以得到:h[n-k]=H{δ[n-k]},从而带入上式中可得:

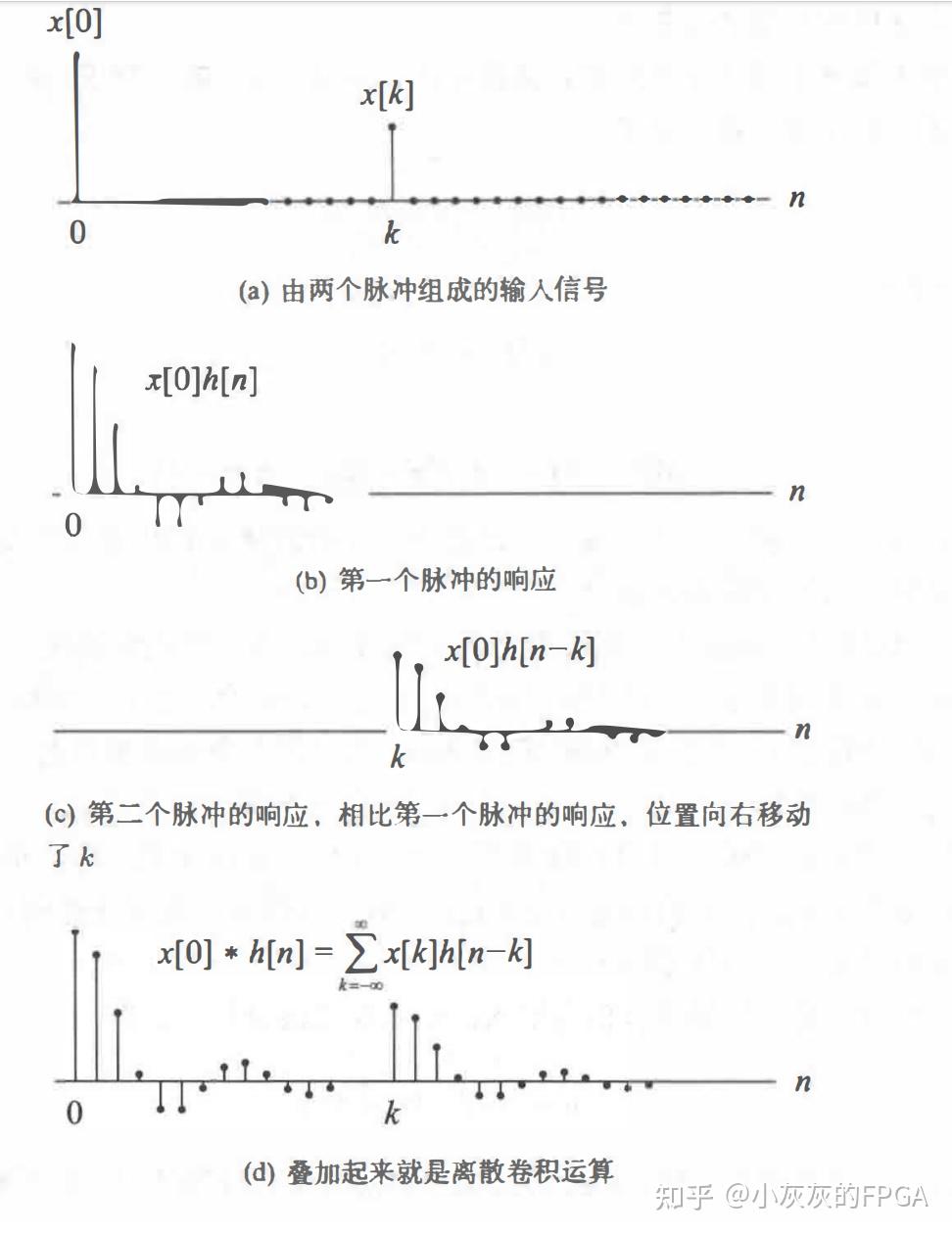
 上式也就是所谓的离散卷积,y[n]=x[n]*h[n]。其中h[n]指的是系统的冲激响应,反映了系统的特性,也就是说系统的输出是输入和冲激响应的卷积。 如何理解离散卷积的计算过程? 输入信号为两个脉冲,第一个脉冲位于位置0处,产生一个响应x[0]h[n],第二个脉冲位置在k处,产生一个响应x[k]h[n-k],系统的输出,也就是所谓的卷积运算,是把两个响应求和。
上式也就是所谓的离散卷积,y[n]=x[n]*h[n]。其中h[n]指的是系统的冲激响应,反映了系统的特性,也就是说系统的输出是输入和冲激响应的卷积。 如何理解离散卷积的计算过程? 输入信号为两个脉冲,第一个脉冲位于位置0处,产生一个响应x[0]h[n],第二个脉冲位置在k处,产生一个响应x[k]h[n-k],系统的输出,也就是所谓的卷积运算,是把两个响应求和。

 n时刻系统的输出信号只与该时刻之前的输入信号有关,和该时刻之后的输入信号无关,因此求和的上限可以取n。
n时刻系统的输出信号只与该时刻之前的输入信号有关,和该时刻之后的输入信号无关,因此求和的上限可以取n。

 3、连续δ信号 连续δ信号,也称为“狄拉克函数”或者“冲激函数”。冲激函数零点的值是无穷,其他位置的值都是零,也就是说在无穷时间上的积分为单位1,具体的公式如下:
3、连续δ信号 连续δ信号,也称为“狄拉克函数”或者“冲激函数”。冲激函数零点的值是无穷,其他位置的值都是零,也就是说在无穷时间上的积分为单位1,具体的公式如下:

 4、连续卷积 假设一个系统y(t)=H{x(t)},其中x(t)为输入信号,y(t)为输出信号,h(t)为系统对δ信号的响应,即:h(t)=H{δ(t)}。
4、连续卷积 假设一个系统y(t)=H{x(t)},其中x(t)为输入信号,y(t)为输出信号,h(t)为系统对δ信号的响应,即:h(t)=H{δ(t)}。

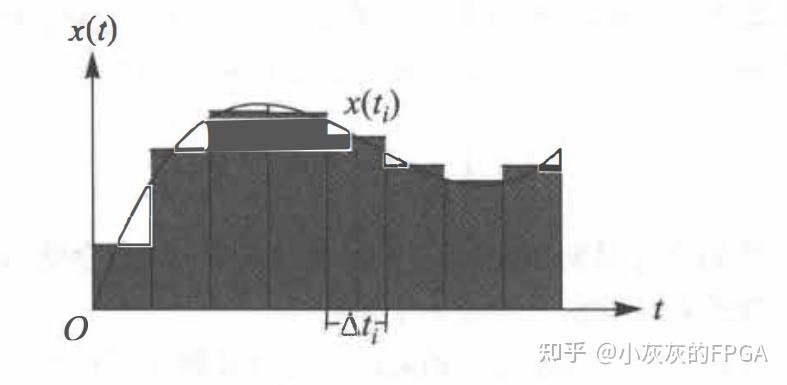
 如何理解连续卷积? 一个连续信号,通过多段的阶梯信号来逼近,将横坐标t划分成很多的小段,保证每一段内的信号水平值差不多,选择一个数值作为此段的代表,从而形成一个阶梯信号。如果每个小段的长度都趋近于零,那么阶梯信号就无限逼近于输入信号x(t)。 将等效的阶梯信号作为系统输入时,每个小的阶梯信号都会产生一个对应的输出信号。当然,等效后的阶梯信号是所有小阶梯信号的和,那么所有小阶梯信号的输出信号的和就是这个等效阶梯信号的输出响应。
如何理解连续卷积? 一个连续信号,通过多段的阶梯信号来逼近,将横坐标t划分成很多的小段,保证每一段内的信号水平值差不多,选择一个数值作为此段的代表,从而形成一个阶梯信号。如果每个小段的长度都趋近于零,那么阶梯信号就无限逼近于输入信号x(t)。 将等效的阶梯信号作为系统输入时,每个小的阶梯信号都会产生一个对应的输出信号。当然,等效后的阶梯信号是所有小阶梯信号的和,那么所有小阶梯信号的输出信号的和就是这个等效阶梯信号的输出响应。

 如何推导并证明连续卷积? 将连续信号分解成N个阶梯,第i个阶梯的信号数值为x(ti),对应的阶梯宽度为∆ti,则这个矩形脉冲的面积为x(ti)×∆ti。用hi(t)表示宽度为∆ti,面积为1的矩形脉冲的输出,则根据线性系统的数乘性,可知面积为x(ti)×∆ti的脉冲信号的输出x(ti)×∆ti×hi(t)。当单位面积的矩形脉冲的宽度趋近于零时,此时矩形脉冲为冲激信号δ(t),系统对它的响应hi(t)逼近于冲激响应h(t),也就得到x(ti)×∆ti×h(t)。根据线性系统的时不变特性,将系统的响应h(t)右移ti,则可得到x(ti)×∆ti×h(t-ti)。将所有的小脉冲的响应累加就是系统对x(t)的响应,公式为:
如何推导并证明连续卷积? 将连续信号分解成N个阶梯,第i个阶梯的信号数值为x(ti),对应的阶梯宽度为∆ti,则这个矩形脉冲的面积为x(ti)×∆ti。用hi(t)表示宽度为∆ti,面积为1的矩形脉冲的输出,则根据线性系统的数乘性,可知面积为x(ti)×∆ti的脉冲信号的输出x(ti)×∆ti×hi(t)。当单位面积的矩形脉冲的宽度趋近于零时,此时矩形脉冲为冲激信号δ(t),系统对它的响应hi(t)逼近于冲激响应h(t),也就得到x(ti)×∆ti×h(t)。根据线性系统的时不变特性,将系统的响应h(t)右移ti,则可得到x(ti)×∆ti×h(t-ti)。将所有的小脉冲的响应累加就是系统对x(t)的响应,公式为:

 t时刻系统的输出信号只与该时刻前的输入信号有关,积分的上限取t,则y(t)可以表示为:
t时刻系统的输出信号只与该时刻前的输入信号有关,积分的上限取t,则y(t)可以表示为:

 y(t)是t时刻系统的输出信号,是由t时刻之前的输入信号的无数的小冲激脉冲引起的,积分上限为t,积分变量为τ,时刻τ处的一个冲激脉冲,强度为x(τ)dτ,所引起的系统输出为x(τ)dτ×h(t-τ),也就是将冲激响应的波形右移τ,然后通过积分后得到y(t)。 二、卷积性质 1、交换律
y(t)是t时刻系统的输出信号,是由t时刻之前的输入信号的无数的小冲激脉冲引起的,积分上限为t,积分变量为τ,时刻τ处的一个冲激脉冲,强度为x(τ)dτ,所引起的系统输出为x(τ)dτ×h(t-τ),也就是将冲激响应的波形右移τ,然后通过积分后得到y(t)。 二、卷积性质 1、交换律

 2、分配律
2、分配律

 3、结合律
3、结合律

 4、与冲激函数卷积
4、与冲激函数卷积

 我来趣味化地解释下卷积的具体应用。 卷积神经网络,是神经网络中的一种,它在至少1层中,把矩阵乘法(matrix multiplication)变成了卷积运算。相比于常规神经网络,它存在的主要意义是:使用filter(也称kernel), 能成功挖掘出图像(data grid)中的空间依赖性(spatial dependencies)。即如果我是图像中的一点,我和周围的点的颜色深浅关系,也构成了图片的特征之一(如我们一起形成了一个角或边),而普通的神经网络,在input时,会把我和邻近点信息分开独立地传进去,很难考虑我和邻近点之间的关系为易于处理图像,可以降低图像(data grid)的大小,但不会失去做预测判断的重要图像特征。即如果需要把我和其他人的图片区别开来,它会选择强化主要特征(如眼睛),并会弱化不重要的特征(如毛孔),通过弱化特征和减小图像尺寸,图像自然就变小了 那么问题来了,图像中到底哪些是重要特征,哪些是不重要特征呢?例如需要区分马蒂斯和塞尚的人物画,人类也许可以从笔触、色彩等多方面做主观判断,但是否能量化成合适的filter呢(如笔触更明显的是马蒂斯),但是不能被人眼明显识别的特征(如阴影表现),是否就不重要了呢?
我来趣味化地解释下卷积的具体应用。 卷积神经网络,是神经网络中的一种,它在至少1层中,把矩阵乘法(matrix multiplication)变成了卷积运算。相比于常规神经网络,它存在的主要意义是:使用filter(也称kernel), 能成功挖掘出图像(data grid)中的空间依赖性(spatial dependencies)。即如果我是图像中的一点,我和周围的点的颜色深浅关系,也构成了图片的特征之一(如我们一起形成了一个角或边),而普通的神经网络,在input时,会把我和邻近点信息分开独立地传进去,很难考虑我和邻近点之间的关系为易于处理图像,可以降低图像(data grid)的大小,但不会失去做预测判断的重要图像特征。即如果需要把我和其他人的图片区别开来,它会选择强化主要特征(如眼睛),并会弱化不重要的特征(如毛孔),通过弱化特征和减小图像尺寸,图像自然就变小了 那么问题来了,图像中到底哪些是重要特征,哪些是不重要特征呢?例如需要区分马蒂斯和塞尚的人物画,人类也许可以从笔触、色彩等多方面做主观判断,但是否能量化成合适的filter呢(如笔触更明显的是马蒂斯),但是不能被人眼明显识别的特征(如阴影表现),是否就不重要了呢?

 左:马蒂斯作品 右:塞尚作品 答案是:让神经网络自己学习,并自己选择适合的filter
左:马蒂斯作品 右:塞尚作品 答案是:让神经网络自己学习,并自己选择适合的filter

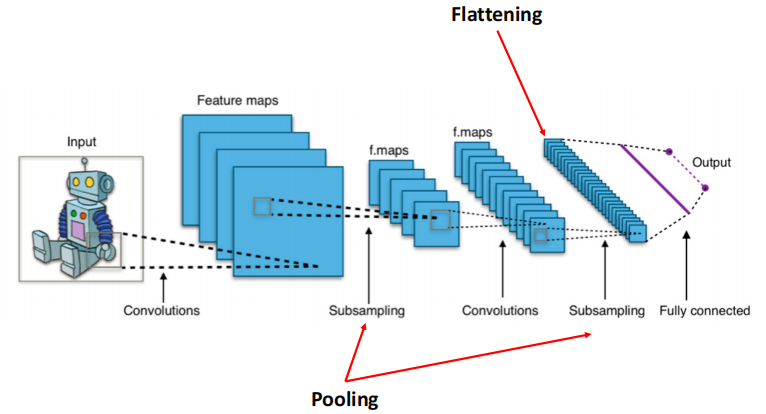
 来源:Wiki,卷积神经网络图示 以上是卷积神经网络(CNN)的各层示意图,而其Output输出的则是一个带有图片特征的向量,被传入常规的神经网络,来判断是哪位画家的作品,并基于预测结果误差,再通过反向传播(backpropagation)来选择适合的filter,并优化ANN的权重
来源:Wiki,卷积神经网络图示 以上是卷积神经网络(CNN)的各层示意图,而其Output输出的则是一个带有图片特征的向量,被传入常规的神经网络,来判断是哪位画家的作品,并基于预测结果误差,再通过反向传播(backpropagation)来选择适合的filter,并优化ANN的权重

 连接了CNN的ANN 知乎上对filter的解释很多,不过要直观感受filter的作用,你可以自己试试这个有趣的工具(前往),如果你选择数字0形状为图片内容,左侧每一个data grid格子中的值(0-1)代表颜色深浅,经过filter卷积运算后,会 输出右侧处理后的图片data grid
连接了CNN的ANN 知乎上对filter的解释很多,不过要直观感受filter的作用,你可以自己试试这个有趣的工具(前往),如果你选择数字0形状为图片内容,左侧每一个data grid格子中的值(0-1)代表颜色深浅,经过filter卷积运算后,会 输出右侧处理后的图片data grid

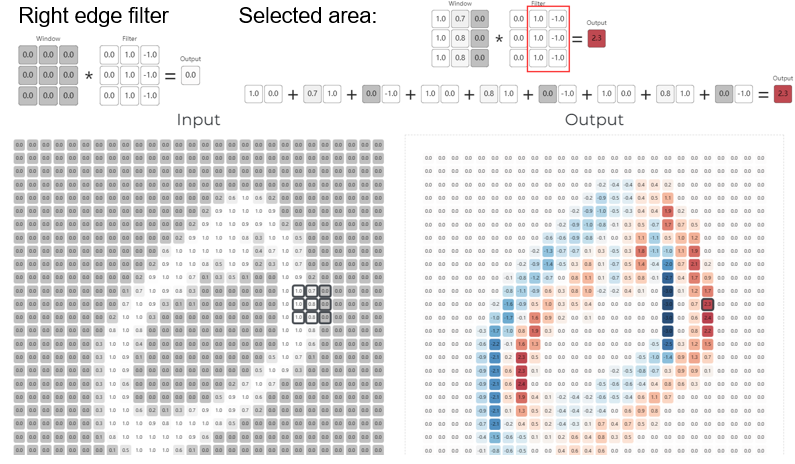
 来源:Deeplizard 每个filter 提取的特征不同,例如提取右侧竖边的filter(right edge filter),每一列的值分别是0, 1,-1,它有什么用呢?以下图左侧选中的这9个点为例,最左侧的3个1,乘以filter矩阵中第一列的3个0后,加总为0,中间的0.7,0.8,0.8,分别乘以filter第二列的1,即加总后为0.7*1+0.8*1+0.8*1=2.3, 右侧的3个0乘以filter最右边列中的-1,加总后也是0, 即左图中选择的9个点,被卷积运算处理后,左侧和右侧共6个点的信息被弱化了,而中间一列点的信息得到了保留及加强(体现在output中,9个点的信息汇集到了左顶点,其数值从1变成了2.3)
来源:Deeplizard 每个filter 提取的特征不同,例如提取右侧竖边的filter(right edge filter),每一列的值分别是0, 1,-1,它有什么用呢?以下图左侧选中的这9个点为例,最左侧的3个1,乘以filter矩阵中第一列的3个0后,加总为0,中间的0.7,0.8,0.8,分别乘以filter第二列的1,即加总后为0.7*1+0.8*1+0.8*1=2.3, 右侧的3个0乘以filter最右边列中的-1,加总后也是0, 即左图中选择的9个点,被卷积运算处理后,左侧和右侧共6个点的信息被弱化了,而中间一列点的信息得到了保留及加强(体现在output中,9个点的信息汇集到了左顶点,其数值从1变成了2.3)

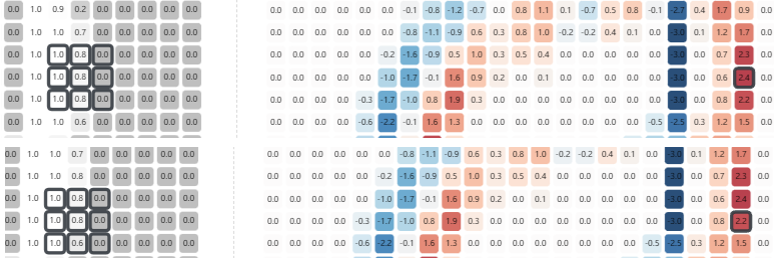
 如果把左侧选中的3 x 3区域下移,分别得到了2.4和2.2,原图中,可以发现,右侧边缘的这几个点,信息同样得到了加强
如果把左侧选中的3 x 3区域下移,分别得到了2.4和2.2,原图中,可以发现,右侧边缘的这几个点,信息同样得到了加强

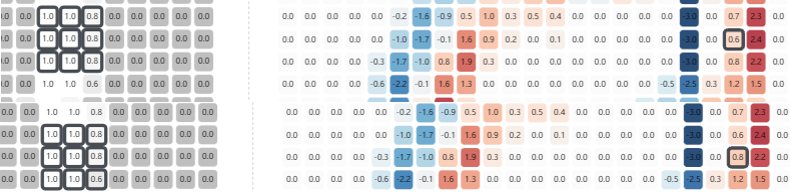
 但如果把左侧选中区域向左边移动1格,会发现汇总到左顶点的数值,从1下降到了0.6和0.8,即对于right edge filter来说,非右侧边缘点的信息受到了减弱(dampen)
但如果把左侧选中区域向左边移动1格,会发现汇总到左顶点的数值,从1下降到了0.6和0.8,即对于right edge filter来说,非右侧边缘点的信息受到了减弱(dampen)

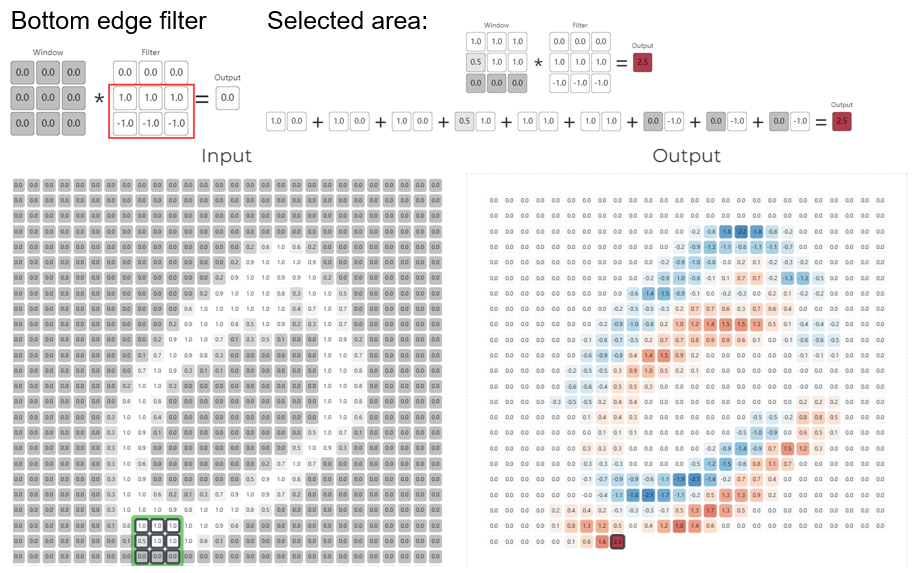
 类似的,如换成提取底部边的filter(bottom edge filter),3×3矩阵变成了第二行是1,第三行为-1,卷积运算后, 原图左右两侧边的信息被弱化到接近于0,但是底部边的信息会被加强到2左右。
类似的,如换成提取底部边的filter(bottom edge filter),3×3矩阵变成了第二行是1,第三行为-1,卷积运算后, 原图左右两侧边的信息被弱化到接近于0,但是底部边的信息会被加强到2左右。

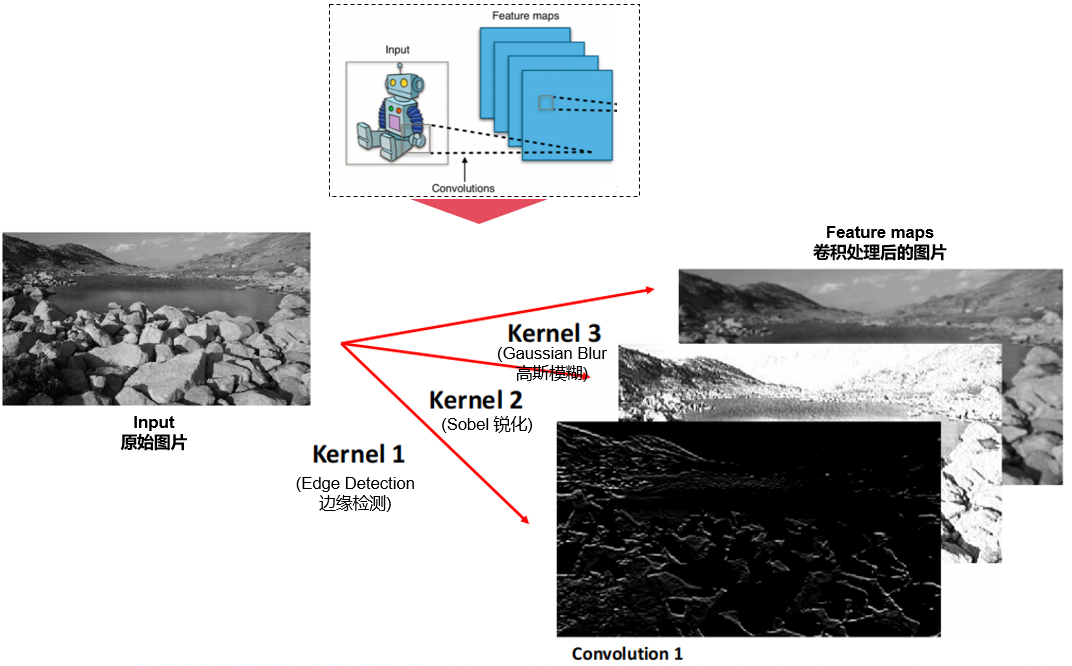
 经过不同的filter(kernel)处理后,图片也会呈现出不同的效果,如被被提取边缘,锐化或高斯模糊等,然后作为Feature maps,再被做subsampling(抽样)
经过不同的filter(kernel)处理后,图片也会呈现出不同的效果,如被被提取边缘,锐化或高斯模糊等,然后作为Feature maps,再被做subsampling(抽样)

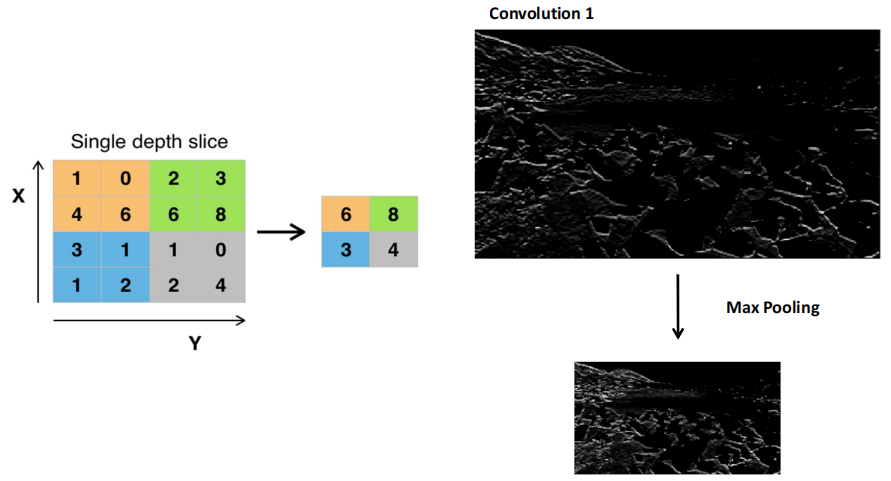
 抽样也有多种方法,以Max pooling 为例,可以在2×2区域内,仅抽取最大值,如下4×4的区域,被Max pooling抽样后,就变成了2×2,处理后的图片仅为原先的1/4,明显减少了图片大小,却保留了其边缘特征
抽样也有多种方法,以Max pooling 为例,可以在2×2区域内,仅抽取最大值,如下4×4的区域,被Max pooling抽样后,就变成了2×2,处理后的图片仅为原先的1/4,明显减少了图片大小,却保留了其边缘特征

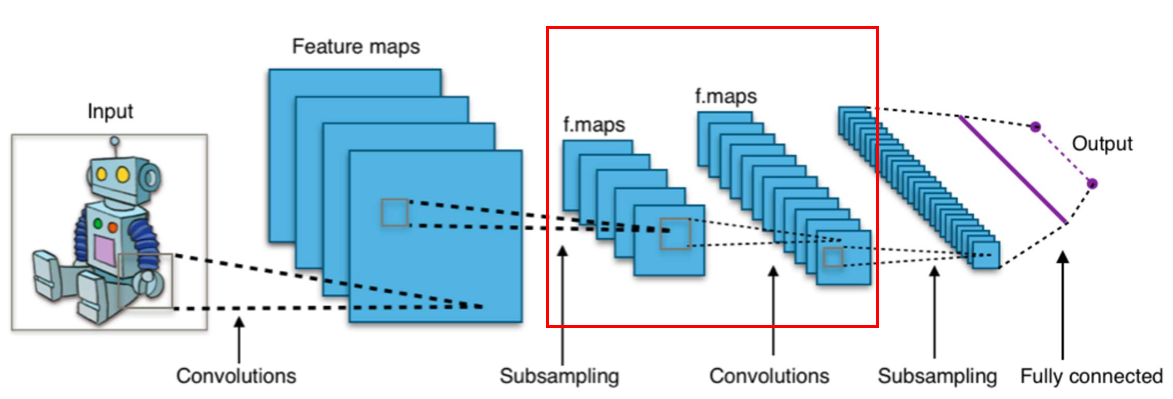
 Max pooling layer 在抽样后,会进行下一次convolution卷积处理(如下红框),那这第2个卷积层,和第1个卷积层有什么不同?
Max pooling layer 在抽样后,会进行下一次convolution卷积处理(如下红框),那这第2个卷积层,和第1个卷积层有什么不同?

 以 Matthew 和 Rob 论文中的卷积层为例,可以发现,第一层主要提取边、对角线等特征,第二层开始有圆弧,角等,第三层提取了形状,到第四、五层提取了明显的物体和人,越往后卷积层提取的图片特征越复杂。
以 Matthew 和 Rob 论文中的卷积层为例,可以发现,第一层主要提取边、对角线等特征,第二层开始有圆弧,角等,第三层提取了形状,到第四、五层提取了明显的物体和人,越往后卷积层提取的图片特征越复杂。

 来源:Visualizing and UnderstandingConvolutional Networks, Matthew D. Zeiler and Rob Fergus 令人兴奋的时刻到了,亲手试试卷积神经网络是怎么工作的吧,这里有个互动demo, 你可以自己来探索下 ; )
来源:Visualizing and UnderstandingConvolutional Networks, Matthew D. Zeiler and Rob Fergus 令人兴奋的时刻到了,亲手试试卷积神经网络是怎么工作的吧,这里有个互动demo, 你可以自己来探索下 ; )

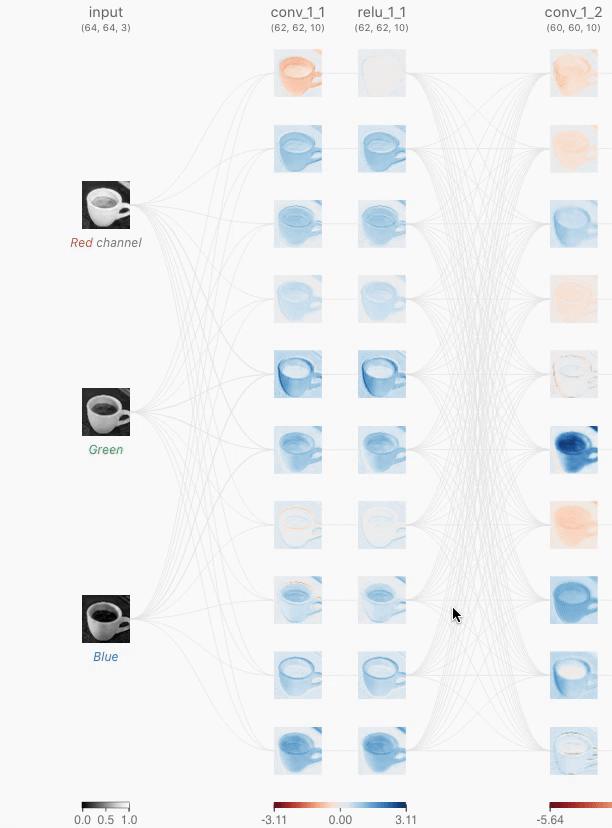
 来源:poloclub.github.io 更多CNN的训练细节,可以参考 Matthew 和 Rob 的论文《Visualizing and Understanding Convolutional Networks》 码字不易,欢迎评论及互动哦~
来源:poloclub.github.io 更多CNN的训练细节,可以参考 Matthew 和 Rob 的论文《Visualizing and Understanding Convolutional Networks》 码字不易,欢迎评论及互动哦~
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。
文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/78758.html



![matlab 数组移位_matlab 左移插图7 [1,1]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![matlab 数组移位_matlab 左移插图9 [1,2]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![matlab 数组移位_matlab 左移插图11 [1,3,2]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)