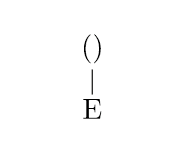
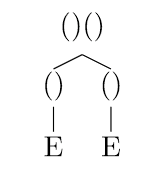
有效的括号是怎么定义的?证明其中一定含有一对紧邻左右括号,将这对括号去掉后剩余的部分也是括号匹配的? 利用栈来判断括号是否匹配,实际上就是不断去除一对紧邻的左右括号,但是怎么证明一个括号匹配的表达式一定含有这样一对紧邻的左右括号?且去除这样一对括号后,不会影响原表达式匹配的判断? 顺便吐槽下小学讲括号时为什么不讲括号匹配的定义,导致现在只会靠肉眼来观察是否匹配。 个人比较喜欢从计算和形象的角度出发考虑这个问题. 由于尽量追求直观/直觉而不是简洁, 所以回答可能会有些长. 考虑题主在其他回答下给出的那种定义:有效的括号表达式,要么是空串””,要么是(A),要么是A+B,其中A、B都是有效的括号表达式。证明:一个括号表达式是匹配的,当且仅当去除其中一对紧邻的左右括号()后,剩余的部分是匹配的。 根据这种定义, 可以为有效表达式定义两对四种运算
 , 其中每对互为逆运算:拼接 – 拆分:
, 其中每对互为逆运算:拼接 – 拆分:
 逆运算:
逆运算:
 套娃 – 脱壳:
套娃 – 脱壳:
 逆运算:
逆运算:
 其中
其中
 和
和
 均为有效表达式. (符号都是随便乱选的, 能明白意思即可, 下同)由于这几种运算都是直接从有效表达式的定义得到的, 下面姑且把它们称作”定义运算”. 有了这个定义运算集合, 和一个人为规定的基本有效表达式”” (简洁直观起见下文写作
均为有效表达式. (符号都是随便乱选的, 能明白意思即可, 下同)由于这几种运算都是直接从有效表达式的定义得到的, 下面姑且把它们称作”定义运算”. 有了这个定义运算集合, 和一个人为规定的基本有效表达式”” (简洁直观起见下文写作
 , 取之意), 我们就可以仅利用正运算自由生成所有满足定义的有效表达式了(为什么强调正运算, 埋个伏笔). 由于这套定义运算覆盖了有效表达式的所有定义情况, 显然一个有效表达式必然能由其他有效表达式通过定义运算得到, 或者说定义运算集的结果集合=全体有效表达式. 而题主的疑惑本质上是另一个大问题的一小部分. 这个问题是这样的: 如果我换一种运算集
, 取之意), 我们就可以仅利用正运算自由生成所有满足定义的有效表达式了(为什么强调正运算, 埋个伏笔). 由于这套定义运算覆盖了有效表达式的所有定义情况, 显然一个有效表达式必然能由其他有效表达式通过定义运算得到, 或者说定义运算集的结果集合=全体有效表达式. 而题主的疑惑本质上是另一个大问题的一小部分. 这个问题是这样的: 如果我换一种运算集
 其中只有一套互逆运算, 定义为: 插入 – 删除
其中只有一套互逆运算, 定义为: 插入 – 删除
 逆运算:
逆运算:
 这个运算集合是从导致题主疑惑的”利用栈判断有效表达式”算法里得到的, 姑且叫做”算法运算”. 其中
这个运算集合是从导致题主疑惑的”利用栈判断有效表达式”算法里得到的, 姑且叫做”算法运算”. 其中
 为有效表达式. 注意
为有效表达式. 注意
 与
与
 本身并不一定是有效表达式, 例如
本身并不一定是有效表达式, 例如
 . 那么, 同样仅从
. 那么, 同样仅从
 出发, 这个运算集是否和定义运算
出发, 这个运算集是否和定义运算
 等价? 换句话说, 是否总能用其中一组的运算来实现另一组运算? 至于为什么问题可以这么解读, 更具体地来说, 问题可以分为两部分:算法运算的表达能力是否大于等于定义运算? 如果答案为是, 那么我们总可以通过算法运算来”模拟”所有定义运算, 这意味着算法运算的结果集合是定义运算的结果集合的父集, 而后者从定义上就是全体有效表达式. 所以证明这一部分将意味着: 不存在算法运算无法得到的有效表达式. 2. 算法运算的表达能力是否小于等于定义运算? 如果答案为是, 那么这意味着算法运算无法得到有效表达式之外的结果. 二者结合,自然也就可以证明算法运算只能得到有效表达式且可以得到每一个有效表达式, 我们也就证明了算法运算和定义运算是等价的. 说清楚问题之后, 证明反而是比较无聊的部分了: 要达成这两个目标有很多方法. 在这篇回答里, 我们尝试进行两次构造性证明:证明定义运算可以模拟所有算法运算再次提示, 这证明了
等价? 换句话说, 是否总能用其中一组的运算来实现另一组运算? 至于为什么问题可以这么解读, 更具体地来说, 问题可以分为两部分:算法运算的表达能力是否大于等于定义运算? 如果答案为是, 那么我们总可以通过算法运算来”模拟”所有定义运算, 这意味着算法运算的结果集合是定义运算的结果集合的父集, 而后者从定义上就是全体有效表达式. 所以证明这一部分将意味着: 不存在算法运算无法得到的有效表达式. 2. 算法运算的表达能力是否小于等于定义运算? 如果答案为是, 那么这意味着算法运算无法得到有效表达式之外的结果. 二者结合,自然也就可以证明算法运算只能得到有效表达式且可以得到每一个有效表达式, 我们也就证明了算法运算和定义运算是等价的. 说清楚问题之后, 证明反而是比较无聊的部分了: 要达成这两个目标有很多方法. 在这篇回答里, 我们尝试进行两次构造性证明:证明定义运算可以模拟所有算法运算再次提示, 这证明了
 2. 证明算法运算可以模拟所有定义运算这证明了
2. 证明算法运算可以模拟所有定义运算这证明了
 综合两个推论便能证明
综合两个推论便能证明
 . 通过定义运算模拟算法运算 首先模拟插入操作. 考虑表达式
. 通过定义运算模拟算法运算 首先模拟插入操作. 考虑表达式
 , 现在希望通过
, 现在希望通过
 实现
实现
 . 其中
. 其中
 为有效表达式. 分类讨论: 若
为有效表达式. 分类讨论: 若
 与
与
 均为有效表达式: 最简单的情况, 可以直接连续应用
均为有效表达式: 最简单的情况, 可以直接连续应用
 运算来模拟插入(我们规定
运算来模拟插入(我们规定
 运算符左结合):
运算符左结合):
 若
若
 其中之一为无效表达式: 考虑逆运算
其中之一为无效表达式: 考虑逆运算
 , 我们知道
, 我们知道
 与
与
 均有效, 但却通过定义运算得到了无效结果
均有效, 但却通过定义运算得到了无效结果
 , 这是不可能的. 同理, 仅
, 这是不可能的. 同理, 仅
 为无效表达式的情况也不存在. 这两种情况舍去. 若
为无效表达式的情况也不存在. 这两种情况舍去. 若
 与
与
 均为无效表达式: 这种情况稍微复杂一些. 由于
均为无效表达式: 这种情况稍微复杂一些. 由于
 是有效表达式, 我们总是能通过两种逆运算
是有效表达式, 我们总是能通过两种逆运算
 实现括号数量的减少, 且结果仍然是有效表达式. 简单来说, 最初
实现括号数量的减少, 且结果仍然是有效表达式. 简单来说, 最初
 是如何通过正运算
是如何通过正运算
 从
从
 构建的, 我们就如何通过相应的逆运算拆回去. 举一些例子, 对于
构建的, 我们就如何通过相应的逆运算拆回去. 举一些例子, 对于
 , 可以拆成
, 可以拆成

 对
对
 则有
则有

 对
对
 会拆解成
会拆解成

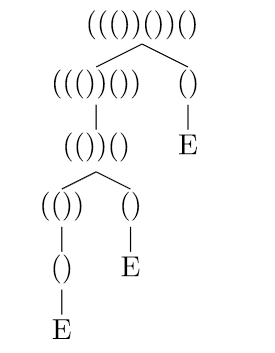
 依此类推.思考题(bushi): 尝试正式地写出上面的拆解算法 为什么要拆解呢? 不妨考虑一个有效表达式
依此类推.思考题(bushi): 尝试正式地写出上面的拆解算法 为什么要拆解呢? 不妨考虑一个有效表达式
 , 其中
, 其中
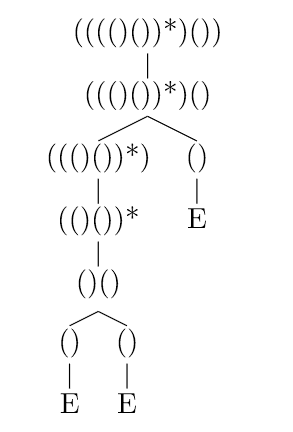
 表示待插入的位置. 将原表达式进行如下拆解:
表示待插入的位置. 将原表达式进行如下拆解:

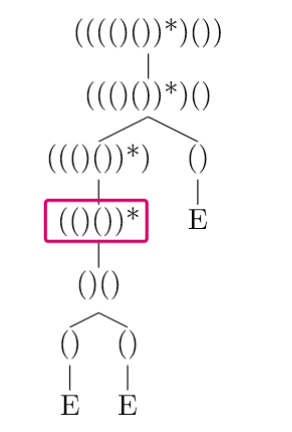
 看起来着实让人眼花, 但我们只需要关心这个位置:
看起来着实让人眼花, 但我们只需要关心这个位置:

 注意到插入位置本身到达了最外层, 与表达式的剩余部分形成了并列关系. 这意味着, 如果将原表达式先拆解到这一层, 则插入操作可以通过
注意到插入位置本身到达了最外层, 与表达式的剩余部分形成了并列关系. 这意味着, 如果将原表达式先拆解到这一层, 则插入操作可以通过
 运算模拟, 即
运算模拟, 即
 接下来, 将修改后的结果再次通过相应的正运算搭建处理, 也就是再自底向上回到树的根部. 容易证明两种正运算
接下来, 将修改后的结果再次通过相应的正运算搭建处理, 也就是再自底向上回到树的根部. 容易证明两种正运算
 均不会破坏已经存在的
均不会破坏已经存在的
 , 所以最终”插入”结果将得到保留, 也就会得到目标表达式. 具体画出来的话是这样的:
, 所以最终”插入”结果将得到保留, 也就会得到目标表达式. 具体画出来的话是这样的:

 左: 逆运算拆解直到*到达最外层; 右: +运算添加括号后原路返回, 可重新构建得到目标 这种转化的唯一要求是插入位置在最外层, 与剩余有效表达式并列, 左右无所谓. 很好, 看来我们接下来要做的大约就是证明对任意有效表达式均存在同一过程, 即插入位置
左: 逆运算拆解直到*到达最外层; 右: +运算添加括号后原路返回, 可重新构建得到目标 这种转化的唯一要求是插入位置在最外层, 与剩余有效表达式并列, 左右无所谓. 很好, 看来我们接下来要做的大约就是证明对任意有效表达式均存在同一过程, 即插入位置
 总会在连续逆运算中的某一步到达最外层. 为了尝试证明这一点, 需要意识到任何含有
总会在连续逆运算中的某一步到达最外层. 为了尝试证明这一点, 需要意识到任何含有
 对括号的表达式内含有
对括号的表达式内含有
 块区域, 而插入位置
块区域, 而插入位置
 必须位于其中之一内. 分别考虑两种逆运算
必须位于其中之一内. 分别考虑两种逆运算
 , 容易证明每进行一次逆运算, 都会干掉至少一对括号, 使得两个区域与最外层合并. 无论如何, 逆运算会使结果的区域总数减少. 逆运算的最终结果全部为基本表达式
, 容易证明每进行一次逆运算, 都会干掉至少一对括号, 使得两个区域与最外层合并. 无论如何, 逆运算会使结果的区域总数减少. 逆运算的最终结果全部为基本表达式
 , 即
, 即
 对括号、
对括号、
 块区域——这块区域自身就是 “最外层”. 随着逆运算拆解的不断进行, 每一条路径上区域数量从初始的
块区域——这块区域自身就是 “最外层”. 随着逆运算拆解的不断进行, 每一条路径上区域数量从初始的
 下降到最后的
下降到最后的
 , 意味着其他
, 意味着其他
 个区域均在中间的某个时刻与剩下的最外层合并了或分岔到其他路径了. 因为我们只关心
个区域均在中间的某个时刻与剩下的最外层合并了或分岔到其他路径了. 因为我们只关心
 所在的那条路径, 所以”分岔到其他路径”的情况不在考虑范围内. 如此一来, 对于每个区域中的
所在的那条路径, 所以”分岔到其他路径”的情况不在考虑范围内. 如此一来, 对于每个区域中的
 , 上述转化过程在路径上必然是存在的——我们总是可以先用一系列逆运算使插入位置
, 上述转化过程在路径上必然是存在的——我们总是可以先用一系列逆运算使插入位置
 在某一步移动到最外层, 然后通过
在某一步移动到最外层, 然后通过
 在该位置插入新的括号, 再通过相应的正运算搭建还原目标表达式. 这就证明了上述例子里的模拟算法是可以普遍应用的.值得注意的是, 这种插入运算模拟的构造方案并没有用到上面
在该位置插入新的括号, 再通过相应的正运算搭建还原目标表达式. 这就证明了上述例子里的模拟算法是可以普遍应用的.值得注意的是, 这种插入运算模拟的构造方案并没有用到上面
 与
与
 均为无效表达式的条件, 也就是说这种构造其实对任意有效
均为无效表达式的条件, 也就是说这种构造其实对任意有效
 均可行. 只不过对于
均可行. 只不过对于
 与
与
 均有效的情况, 前文直接连续
均有效的情况, 前文直接连续
 的方法要简单得多. 到这里我们成功构造了一套仅通过定义运算
的方法要简单得多. 到这里我们成功构造了一套仅通过定义运算
 实现插入运算
实现插入运算
 的方法. 接下来继续模拟插入运算的逆运算, 删除运算
的方法. 接下来继续模拟插入运算的逆运算, 删除运算
 . 考虑删除操作
. 考虑删除操作
 , 尝试用定义运算模拟它. 其中
, 尝试用定义运算模拟它. 其中
 为有效表达式. 另外由上面已经证明的结论,
为有效表达式. 另外由上面已经证明的结论,
 作为
作为
 的结果, 也一定是有效表达式, 因为后者可以被转化为纯定义运算. 因为操作数
的结果, 也一定是有效表达式, 因为后者可以被转化为纯定义运算. 因为操作数
 和
和
 自身仍然不一定有效, 所以同样需要分类讨论. 虽然这个过程有点痛苦, 但是由于证明过程很大程度上可以参考前半段, 实际上颇有似曾相识的感觉.若
自身仍然不一定有效, 所以同样需要分类讨论. 虽然这个过程有点痛苦, 但是由于证明过程很大程度上可以参考前半段, 实际上颇有似曾相识的感觉.若
 与
与
 均为有效表达式: 和前半段一样, 这仍然是最简单的情况, 可以直接写出:
均为有效表达式: 和前半段一样, 这仍然是最简单的情况, 可以直接写出:
 (规定
(规定
 运算符同样为左结合.) 若
运算符同样为左结合.) 若
 与
与
 其中之一为有效表达式: 和之前一样, 这种情况不可能发生: 如果只有
其中之一为有效表达式: 和之前一样, 这种情况不可能发生: 如果只有
 是无效表达式, 那么注意到
是无效表达式, 那么注意到
![匹配括号js_判断表达式中括号是否匹配插图107 X()Y-()Y=X()Y-[() + Y]=X](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 已知
已知
 均有效, 却通过定义运算得到了无效表达式
均有效, 却通过定义运算得到了无效表达式
 , 这是不可能的, 舍去. 仅
, 这是不可能的, 舍去. 仅
 无效的情况同理. 若
无效的情况同理. 若
 与
与
 均为无效表达式: 和上面模拟插入运算的过程高度相似, 篇幅起见尽量简略说明. 由于
均为无效表达式: 和上面模拟插入运算的过程高度相似, 篇幅起见尽量简略说明. 由于
 有效, 所以总是可以通过连续逆运算将
有效, 所以总是可以通过连续逆运算将
 向下降解, 从而能够在其中某一步使待删除
向下降解, 从而能够在其中某一步使待删除
 位于最外层与剩余表达式并列, 这时便可以通过
位于最外层与剩余表达式并列, 这时便可以通过
 运算删除这一括号; 最后, 通过相应的连续正运算重新构建表达式, 即可得到
运算删除这一括号; 最后, 通过相应的连续正运算重新构建表达式, 即可得到
 . 至此第一部分证明完成: 从有效表达式出发, 定义运算
. 至此第一部分证明完成: 从有效表达式出发, 定义运算
 可以模拟所有算法运算
可以模拟所有算法运算
 ; 也可以说, 对有效表达式进行算法运算只可能得到有效表达式:
; 也可以说, 对有效表达式进行算法运算只可能得到有效表达式:
 实际上题主的问题到这里就得证了 (而且其实只需要后半部分
实际上题主的问题到这里就得证了 (而且其实只需要后半部分
 的内容), 因为我们已经证明可以只用定义运算模拟删除
的内容), 因为我们已经证明可以只用定义运算模拟删除
 的运算
的运算
 , 而定义运算作用于任何有效表达式的结果仍然是有效表达式. 如果在连续
, 而定义运算作用于任何有效表达式的结果仍然是有效表达式. 如果在连续
 的过程中, 到达基本表达式
的过程中, 到达基本表达式
 之前, 就遭遇了某个中间结果使得无法进行
之前, 就遭遇了某个中间结果使得无法进行
 运算, 那么也相应地意味着无法进行翻译得到的定义运算, 这说明此表达式无效, 而这又只可能是因为初始的表达式就是无效表达式. 因此, 首先, 对于有效表达式, 算法一定能输出”有效”的结果. 另一方面, 假设存在一条无效表达式能输出”有效”结果, 即它可以通过连续
运算, 那么也相应地意味着无法进行翻译得到的定义运算, 这说明此表达式无效, 而这又只可能是因为初始的表达式就是无效表达式. 因此, 首先, 对于有效表达式, 算法一定能输出”有效”的结果. 另一方面, 假设存在一条无效表达式能输出”有效”结果, 即它可以通过连续
 运算达到
运算达到
 . 但是我们已经证明,
. 但是我们已经证明,
 运算可以全部翻译为纯的定义运算
运算可以全部翻译为纯的定义运算
 . 如果我们把相应的连续
. 如果我们把相应的连续
 运算全部翻译成定义运算, 则这意味着这条无效表达式通过一系列纯定义运算得到了一条有效表达式
运算全部翻译成定义运算, 则这意味着这条无效表达式通过一系列纯定义运算得到了一条有效表达式
 , 这是不可能的. 因此, 对于无效表达式, 算法一定不能输出”有效”的结果. 综上, 通过判断连续
, 这是不可能的. 因此, 对于无效表达式, 算法一定不能输出”有效”的结果. 综上, 通过判断连续
 能否得到
能否得到
 来判断初始表达式是否有效是可行的.实际上这里还略过了对运算数量的证明, 因为算法的可行性还依赖于运算能否在有限次数到达E. 当然, 证明可以通过考虑括号数量完成, 此处按下不表. 现在, 我们已经证明了定义运算表达能力强于或等于算法运算, 也证明了算法的正确性. 但我们不妨继续尝试进一步证明二者的等价性, 这将意味着二者的表达能力实际上精确相等. 通过定义运算模拟算法运算 开始之前, 设想我们有方法利用一系列插入运算
来判断初始表达式是否有效是可行的.实际上这里还略过了对运算数量的证明, 因为算法的可行性还依赖于运算能否在有限次数到达E. 当然, 证明可以通过考虑括号数量完成, 此处按下不表. 现在, 我们已经证明了定义运算表达能力强于或等于算法运算, 也证明了算法的正确性. 但我们不妨继续尝试进一步证明二者的等价性, 这将意味着二者的表达能力实际上精确相等. 通过定义运算模拟算法运算 开始之前, 设想我们有方法利用一系列插入运算
 得到任意有效表达式
得到任意有效表达式
 , 并将这一系列运算记作
, 并将这一系列运算记作
![匹配括号js_判断表达式中括号是否匹配插图113 f[A]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) , 且
, 且
![匹配括号js_判断表达式中括号是否匹配插图113 f[A]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 的位置指代最终插入结果的位置. 那么问题可分解为两部分:使用
的位置指代最终插入结果的位置. 那么问题可分解为两部分:使用
![匹配括号js_判断表达式中括号是否匹配插图113 f[A]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 模拟定义运算中的正运算
模拟定义运算中的正运算
 ; 2. 证明对任意有效表达式
; 2. 证明对任意有效表达式
 , 一定存在一个
, 一定存在一个
![匹配括号js_判断表达式中括号是否匹配插图113 f[A]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) . 二者结合, 就意味着实现了对任意有效表达式的
. 二者结合, 就意味着实现了对任意有效表达式的
 运算的模拟, 而将它们作用在基本表达式
运算的模拟, 而将它们作用在基本表达式
 上就能给我们带来全体有效表达式了! 下面开始第一部分. 模拟套娃运算
上就能给我们带来全体有效表达式了! 下面开始第一部分. 模拟套娃运算
 :
:
![匹配括号js_判断表达式中括号是否匹配插图117 A\bullet=(A): \\ 第一步: f[()] = ()\\ 第二步: (f[A]) = (A)](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 对于第一步, 实际上可以直接找到一个
对于第一步, 实际上可以直接找到一个
![匹配括号js_判断表达式中括号是否匹配插图119 f[()]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 的精确表达:
的精确表达:
![匹配括号js_判断表达式中括号是否匹配插图121 EE\oplus=E()E=()=f[()]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 所以之后的所有
所以之后的所有
![匹配括号js_判断表达式中括号是否匹配插图119 f[()]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 将直接化简写为
将直接化简写为
 . 上面的模拟运算公式可由此简写为:
. 上面的模拟运算公式可由此简写为:
![匹配括号js_判断表达式中括号是否匹配插图123 A\bullet=(A)=(f[A])](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 模拟拼接运算
模拟拼接运算
 :
:
![匹配括号js_判断表达式中括号是否匹配插图125 A+B=AB=f[A] f[B]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 这一部分可以用无聊来形容. 接下来证明
这一部分可以用无聊来形容. 接下来证明
![匹配括号js_判断表达式中括号是否匹配插图113 f[A]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 对任意有效表达式
对任意有效表达式
 的存在性. 使用数学归纳法. 若
的存在性. 使用数学归纳法. 若
![匹配括号js_判断表达式中括号是否匹配插图113 f[A]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 和
和
![匹配括号js_判断表达式中括号是否匹配插图127 f[B]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 存在, 则
存在, 则
![匹配括号js_判断表达式中括号是否匹配插图129 f[A+B]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 存在. 显然
存在. 显然
![匹配括号js_判断表达式中括号是否匹配插图131 f[A+B]=f[AB]=f[A]f[B]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) , 若后两者存在则前者可通过这种形式构造. 2. 若
, 若后两者存在则前者可通过这种形式构造. 2. 若
![匹配括号js_判断表达式中括号是否匹配插图113 f[A]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 存在, 则
存在, 则
![匹配括号js_判断表达式中括号是否匹配插图133 f[(A)]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 存在. 可以通过以下两步得到
存在. 可以通过以下两步得到
![匹配括号js_判断表达式中括号是否匹配插图133 f[(A)]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) :
:
![匹配括号js_判断表达式中括号是否匹配插图135 1. 通过f[()]生成()\\ 2. 在()内部通过f[A]生成A](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E)
![匹配括号js_判断表达式中括号是否匹配插图119 f[()]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 客观存在 (上面已经找到一个具体表达式), 所以只要
客观存在 (上面已经找到一个具体表达式), 所以只要
![匹配括号js_判断表达式中括号是否匹配插图113 f[A]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 也存在时, 可以通过以上方式构造
也存在时, 可以通过以上方式构造
![匹配括号js_判断表达式中括号是否匹配插图133 f[(A)]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) . 3.
. 3.
![匹配括号js_判断表达式中括号是否匹配插图137 f[E]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 存在 只要对
存在 只要对
 啥也不干就能得到
啥也不干就能得到
 了 (废话文学). 当然, 考虑到最初没有在算法运算集
了 (废话文学). 当然, 考虑到最初没有在算法运算集
 里加入”啥也不干”这种零运算, 也可以显式地用一对逆运算生成
里加入”啥也不干”这种零运算, 也可以显式地用一对逆运算生成
 , 效果一样:
, 效果一样:
![匹配括号js_判断表达式中括号是否匹配插图139 f[E]:EE\oplus\ominus=E](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E) 4. 完成归纳 首先回顾一下: 有效表达式的直接定义是能够从
4. 完成归纳 首先回顾一下: 有效表达式的直接定义是能够从
 通过
通过
 进行连续运算得到的表达式. 根据1和2, 通过构造的方法,
进行连续运算得到的表达式. 根据1和2, 通过构造的方法,
 的存在性在
的存在性在
 运算的操作数和结果中总是具有传递性; 由于任意有效表达式都可以转化为对
运算的操作数和结果中总是具有传递性; 由于任意有效表达式都可以转化为对
 进行
进行
 运算的结果, 而在3中又已经证明对于操作数
运算的结果, 而在3中又已经证明对于操作数
 存在一个
存在一个
 , 那么对于作为运算结果的其他全体有效表达式, 也总是可以分别构造出
, 那么对于作为运算结果的其他全体有效表达式, 也总是可以分别构造出
 . 第二部分到这里就结束了. 我们已经从第一部分知道了算法运算的结果集合是全体有效表达式的子集, 刚刚又证明了算法运算的结果集合是全体有效表达式的父集, 那么二者只可能严格相等. 到这里我们就已经不甚严密但还算直观地证明了上面提出的大问题, 即两种运算在实质上是等价的. 当然还是要啰嗦两三句. 虽然二者等价, 哪个都可以作为定义, 但其实插入-删除运算对应的那个定义更加简单也更基本一些, 这从两个部分证明的自然程度可以比较出来. 另一方面, 从实际应用来说也更加符合实践——数学表达式中的括号往往被理解为一个整体, 更看重的是”取出括号不影响有效性”. 基于以上种种原因, 所以我更倾向于将定义选为一个有效的括号表达式, 要么是”()”, 要么是一个有效表达式中插入了另一个有效括号表达式. 最后预防性甩锅 (bushi, 我没有系统学过代数, 鄙人是学物理的, 所以这些内容纯属想着玩的, 说我是民科也行, 溜了溜了
. 第二部分到这里就结束了. 我们已经从第一部分知道了算法运算的结果集合是全体有效表达式的子集, 刚刚又证明了算法运算的结果集合是全体有效表达式的父集, 那么二者只可能严格相等. 到这里我们就已经不甚严密但还算直观地证明了上面提出的大问题, 即两种运算在实质上是等价的. 当然还是要啰嗦两三句. 虽然二者等价, 哪个都可以作为定义, 但其实插入-删除运算对应的那个定义更加简单也更基本一些, 这从两个部分证明的自然程度可以比较出来. 另一方面, 从实际应用来说也更加符合实践——数学表达式中的括号往往被理解为一个整体, 更看重的是”取出括号不影响有效性”. 基于以上种种原因, 所以我更倾向于将定义选为一个有效的括号表达式, 要么是”()”, 要么是一个有效表达式中插入了另一个有效括号表达式. 最后预防性甩锅 (bushi, 我没有系统学过代数, 鄙人是学物理的, 所以这些内容纯属想着玩的, 说我是民科也行, 溜了溜了
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。
文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/68561.html



















































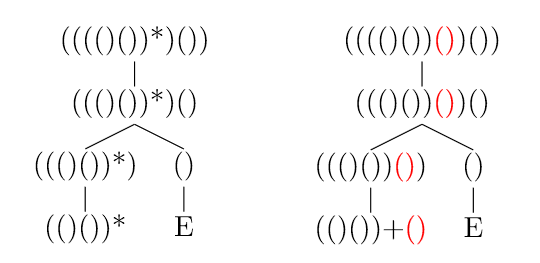





































![匹配括号js_判断表达式中括号是否匹配插图107 X()Y-()Y=X()Y-[() + Y]=X](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)





























![匹配括号js_判断表达式中括号是否匹配插图113 f[A]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![匹配括号js_判断表达式中括号是否匹配插图113 f[A]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![匹配括号js_判断表达式中括号是否匹配插图113 f[A]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)


![匹配括号js_判断表达式中括号是否匹配插图113 f[A]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)



![匹配括号js_判断表达式中括号是否匹配插图117 A\bullet=(A): \\ 第一步: f[()] = ()\\ 第二步: (f[A]) = (A)](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![匹配括号js_判断表达式中括号是否匹配插图119 f[()]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![匹配括号js_判断表达式中括号是否匹配插图121 EE\oplus=E()E=()=f[()]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![匹配括号js_判断表达式中括号是否匹配插图119 f[()]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)

![匹配括号js_判断表达式中括号是否匹配插图123 A\bullet=(A)=(f[A])](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)

![匹配括号js_判断表达式中括号是否匹配插图125 A+B=AB=f[A] f[B]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![匹配括号js_判断表达式中括号是否匹配插图113 f[A]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)

![匹配括号js_判断表达式中括号是否匹配插图113 f[A]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![匹配括号js_判断表达式中括号是否匹配插图127 f[B]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![匹配括号js_判断表达式中括号是否匹配插图129 f[A+B]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![匹配括号js_判断表达式中括号是否匹配插图131 f[A+B]=f[AB]=f[A]f[B]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![匹配括号js_判断表达式中括号是否匹配插图113 f[A]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![匹配括号js_判断表达式中括号是否匹配插图133 f[(A)]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![匹配括号js_判断表达式中括号是否匹配插图133 f[(A)]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![匹配括号js_判断表达式中括号是否匹配插图135 1. 通过f[()]生成()\\ 2. 在()内部通过f[A]生成A](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![匹配括号js_判断表达式中括号是否匹配插图119 f[()]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![匹配括号js_判断表达式中括号是否匹配插图113 f[A]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![匹配括号js_判断表达式中括号是否匹配插图133 f[(A)]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![匹配括号js_判断表达式中括号是否匹配插图137 f[E]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)




![匹配括号js_判断表达式中括号是否匹配插图139 f[E]:EE\oplus\ominus=E](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)











![PhpStorm2024.1.5激活码([转载]PhpStorm2024中文版v2024.1.4 正式版)缩略图 PhpStorm2024.1.5激活码([转载]PhpStorm2024中文版v2024.1.4 正式版)](https://sigusoft.com/wp-content/uploads/2024/08/zy6ga-480x300.png)