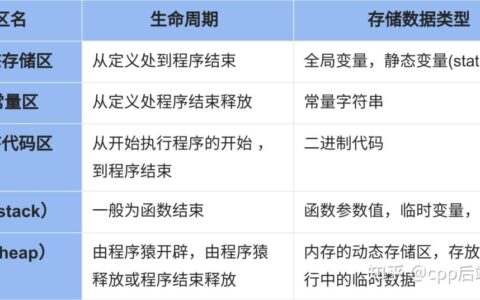
数据结构 具体例子画哈夫曼树和图的邻接矩阵 由于这两个内容相对较少，所以放在一起记录。 哈夫曼树定义：在n个带权叶子节点构成的所有二叉树中，带权路径长度最小的二叉树称为哈夫曼树。 例如，给定4个叶子结点，权值分别为1，3，5，7，可以构造4忠不同的二叉树，如下图所示：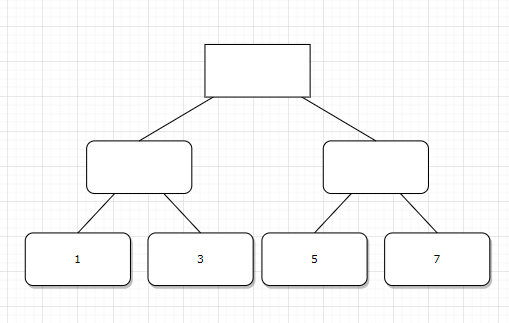
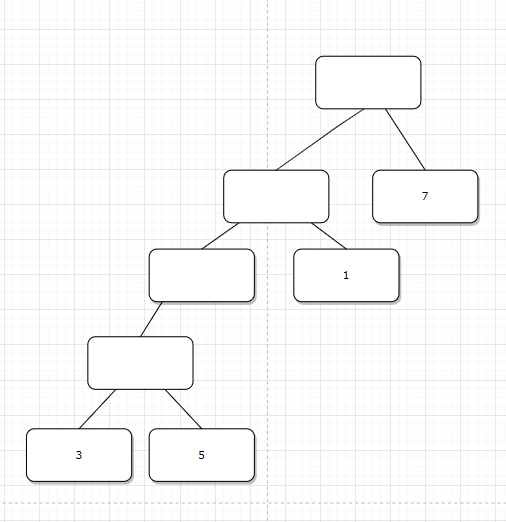
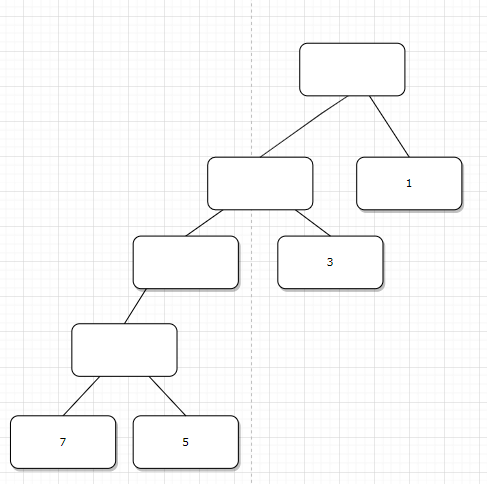
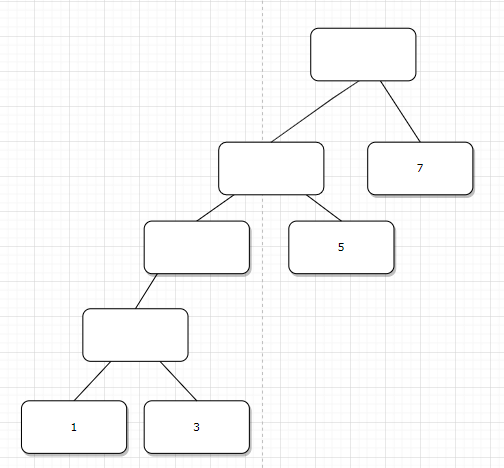其权值分别为：32、33、43、29，由此可见，图4哈夫曼树的带权路径长度最小。 接着来看两道题。 设有a、b、c、d、e、f、g、h几个字母，对应频率为0.07、0.19、0.02、0.06、0.32、0.03、0.21和0.01，试设计哈夫曼树 构造过程如下： 第1步选择频率最低的c和f构造一棵二叉树,其根结点的频率为0. 05，记为结点d1； 第2步选择频率低的d1和d构造一棵二叉树，其根结点的频率为0.11,记为结点d2； 第3步选择频率低的a和h构造一棵二叉树,其根结点的频率为 0.17，记为结点d3； 第4步选择频率低的d2和d3构造一棵二叉树,其根结点的频率为0.28,记为结点d4； 第5步选择频率低的b和g构造一棵二叉树,其根结点的频率为0.4,记为结点d5; 第6步选择频幸低的d4和e构造一棵二叉树，其根结点的频率为 0.6,记为结点d6； 第7步选择领幸低的d5和d6构造一棵二叉树，其根结点的频率为1.0.记为结点d7。 最后构造的哈夫易树如图： 
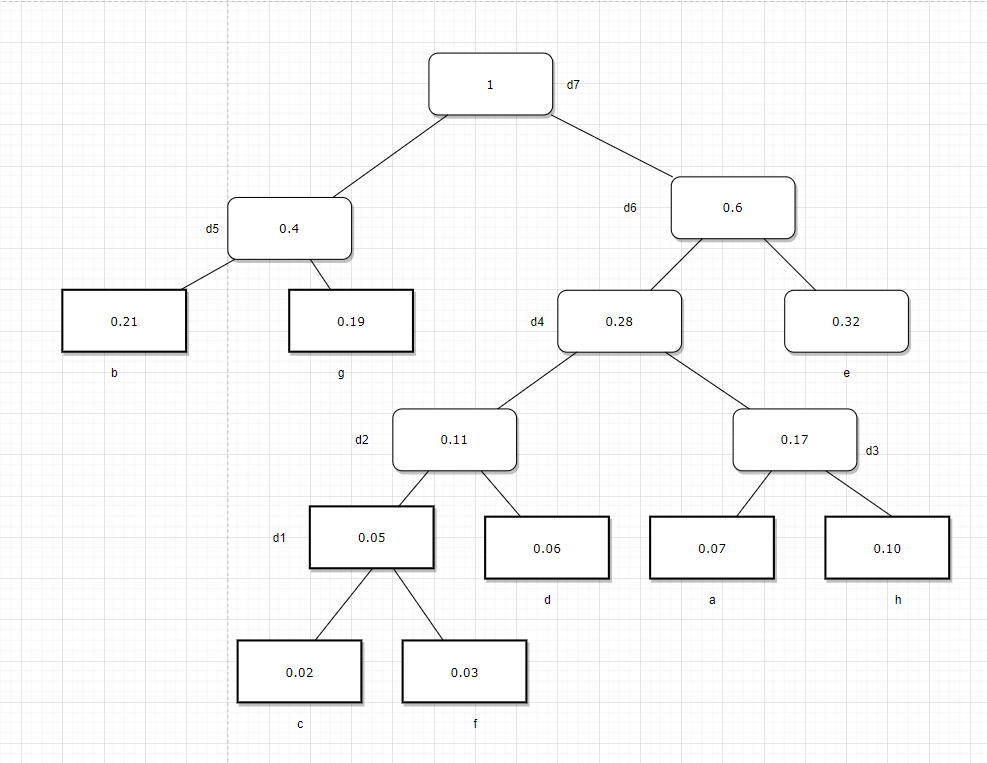2.设有单词the,of,a,to,and,in,that,he,is,at,on,for,his,are,be.对应的频度为:1192,677,541,518,462,450,242,195,190,181,174,157,138,124,123，试设计哈夫曼树。 第1步选择频率最低的be和are构造一棵二叉树,其根结点的频度为247，记为结点d1； 第2步选择频率低的his和for构造一棵二叉树，其根结点的频度为295,记为结点d2； 第3步选择频率低的on和at构造一棵二叉树,其根结点的频度为 355，记为结点d3； 第4步选择频率低的is和he构造一棵二叉树,其根结点的频度为385,记为结点d4； 第5步选择频率低的d1和that构造一棵二叉树,其根结点的频度为489,记为结点d5; 第6步选择频幸低的d2和d3构造一棵二叉树，其根结点的频度为 650,记为结点d6； 第7步选择领幸低的d4和in构造一棵二叉树，其根结点的频度为835.记为结点d7； 第8步选择频率低的d5和and构造一棵二叉树,其根结点的频度为951,记为结点d8； 第9步选择频率低的to和a构造一棵二叉树,其根结点的频度为1059,记为结点d9; 第10步选择频幸低的d6和of构造一棵二叉树，其根结点的频度为 1327,记为结点d10； 第11步选择领幸低的d7和d8构造一棵二叉树，其根结点的频度为1786.记为结点d11； 第12步选择频幸低的d9和the构造一棵二叉树，其根结点的频度为 2251,记为结点d12； 第13步选择领幸低的d10和d11构造一棵二叉树，其根结点的频度为3113.记为结点d13； 第13步选择领幸低的d12和d13构造一棵二叉树，其根结点的频度为5364.记为结点d14； 哈夫曼树如图:
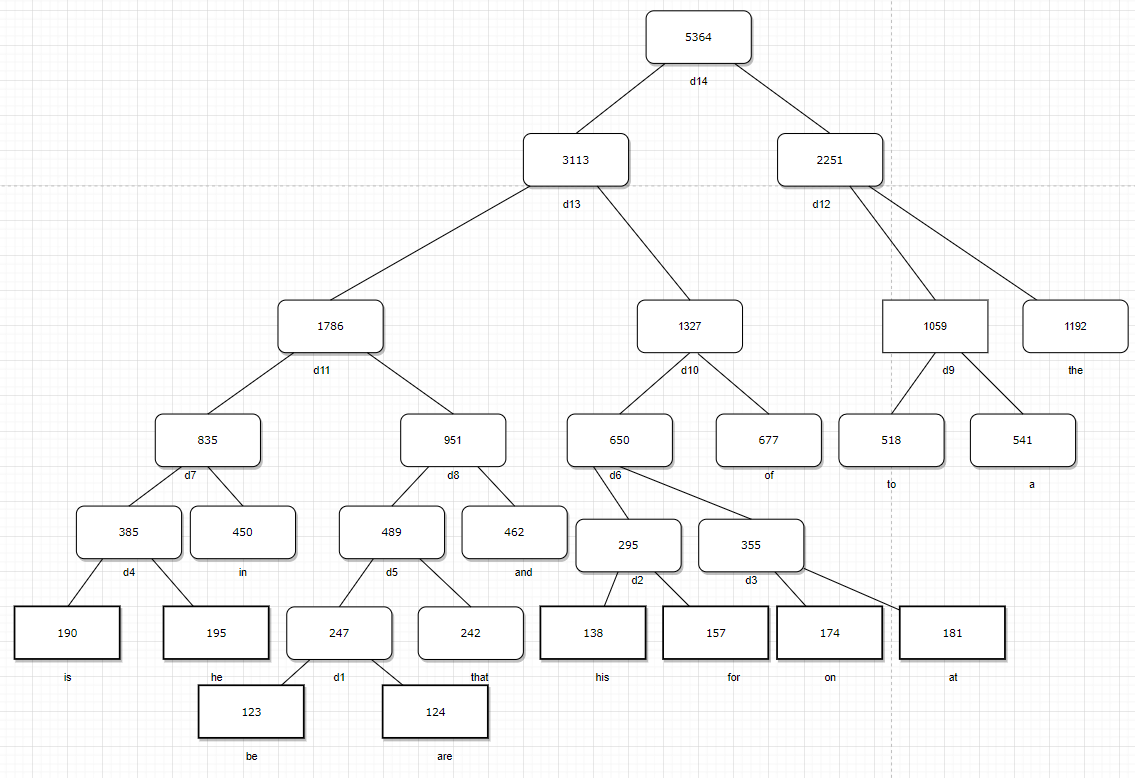邻接矩阵是一种采用邻接矩阵数组表示顶点之间相邻关系的存储结构。 简单点说就是图有连接的的地方矩阵数组就改为1，有向图只有指向的地方才为1； 直接看两个例子：
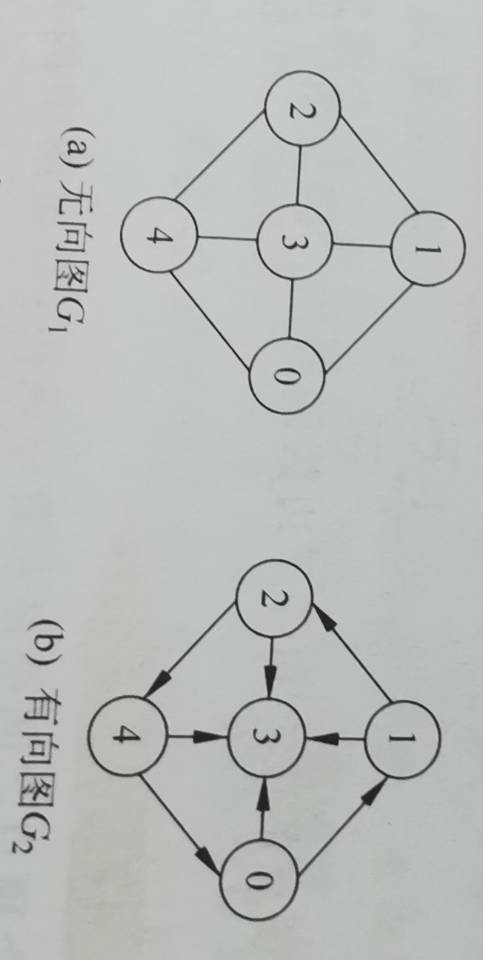图a是无向图G1，图b是有向图G2，分别写出对应的矩阵数组A1和A2；
有错误烦请指正，感谢阅读。
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/68041.html
