jaccard相似性系数_相似性系数的计算公式

样本相似性 – 数据挖掘算法（3）　　样本相似性是指两个或多个样本在某些方面的相似性或接近程度（表现为相对数）。在数据分析和机器学习等领域中，经常需要比较不同样本之间的相似性，以便更好地理解数据或进行更准确的预测。　　相似性（相异性）被许多数据挖掘技术所使用，如聚类、最近邻分类、异常检测等。不同组样本之间的相似度是样本间差异程度的数值度量，两组样本越相似，它们的相异度就越低，相似度越高。通常用各种“相似系数”作为相异度或相似度相异度度量方法。　　一、皮尔逊相关系数(Pearson Correlation coefficient) 　　皮尔逊相关系数也称为简单相关系数，在统计学中，皮尔逊相关系数用于度量两个变量X和Y之间的相关（线性相关）程度，相关系数的取值范围是[-1,1]。相关系数的绝对值越大，则表明X与Y相关度越高，负值表示负相关，正值表示正相关。　　在自然、社会科学领域中，该系数广泛用于度量两个变量之间的相关程度。　　设有m个n维向量
$(X_{k1},X_{k2},\dots,X_{kn}), k=1,2,\dots,m$ ,k=1,2,…,m，向量
$(X_{i1},X_{i2},\dots,X_{in})$ 　　与
$(X_{j1},X_{j2},\dots,X_{jn})$ 间的相关系数公式为：　　
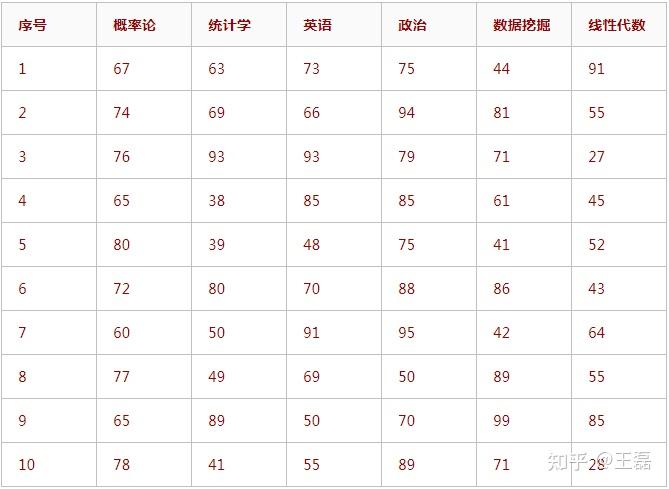
$R_{ij}=\frac{\sum\limits_{k=1}^n(X_{ik}-\overline{X}_i)(X_{jk}-\overline{X}_j)}{\sqrt{(X_{ik}-\overline{X}_i)^2}\sqrt{(X_{jk}-\overline{X}_j)^2}}=\frac{\sum\limits X_{i}X_{j}-\frac{\sum\limits X_{i}\sum\limits X_{j}}{n}}{\sqrt{\sum\limits X_{i}^2-\frac{(\sum\limits X_{i})^2}{n}}\sqrt{\sum\limits X_{j}^2-\frac{(\sum\limits X_{j})^2}{n}}}=\frac{L_{ij}}{\sqrt{L_{ii}L_{jj}}}$ 　　现有10名学生六门课程成绩表如下：

图表1：计算距离时，通常样本数据为数值型　　根据【图表1】中学生成绩表计算第3名和第5名学生成绩之间的皮尔逊相关系数。　　解：第3名成绩向量为A(76,93,93,79,71,27)、第5名成绩向量为B(80,39,48,75,41,52)皮尔逊相关系数，　　
$L_{33}=\sum\limits_{k=1}^mX_{3k}^2-\frac{1}{m}(\sum\limits_{k=1}^mX_{3k})^2=35085-\frac{1}{6}439^2=2964.8333$ 　　
$L_{55}=\sum\limits_{k=1}^mX_{5k}^2-\frac{1}{m}(\sum\limits_{k=1}^mX_{5k})^2=20235-\frac{1}{6}335^2=1530.8333$ 　　
$L_{35}=\sum\limits_{k=1}^mX_{3k}X_{5k}-\frac{1}{m}(\sum\limits_{k=1}^mX_{3k})(\sum\limits_{k=1}^mX_{5k})=24411-\frac{1}{6}439\times 335=-99.8333$ 　　
$R_{35}=\frac{L_{35}}{\sqrt{L_{33}L_{55}}}=\frac{-99.8333}{\sqrt{2964.8333\times 1530.8333}}=-0.12$ 　　皮尔逊相关系数绝对值越小，两组数据相似性越小；相关系数越接近1，两组数据相似性越大；相关系数越接近-1，说明两个同学间各科成绩相反，例如A数学分高而B数学分低，B英语分高而A英语分低。　　同样，可以计算出

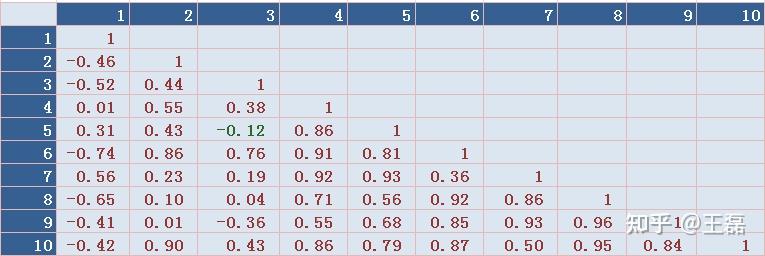
图表2：和距离矩阵不同，此时对角线素为1 　　二、斯皮尔曼秩相关系数（Spearman Rank Correlation）　　斯皮尔曼秩相关系数又称为斯皮尔曼等级相关（Spearman’s correlation coefficient for ranked data）。主要用于解决顺序数据相关的问题。适用于两列变量，而且具有等级变量性质具有线性关系的资料。由英国心理学家、统计学家斯皮尔曼根据积差相关的概念推导而来。斯皮尔曼等级相关系数用来估计两个变量X、Y之间的相关性，其中变量间的相关性可以使用单调函数来描述。如果两个变量取值的两个集合中均不存在相同的两个素，那么，当其中一个变量可以表示为另一个变量的很好的单调函数时（即两个变量的变化趋势相同），两个变量之间的等级相关
$\rho$ 可以达到+1或-1。　　斯皮尔曼等级相关系数对数据条件的要求没有皮尔逊相关系数严格，只要两个变量的观测值是成对的等级评定资料，或者是由连续变量观测资料转化得到的等级资料，不论两个变量的总体分布形态、样本容量的大小如何，都可以用斯皮尔曼等级相关系数来进行研究。　　设有m个n维向量
$(X_{k1},X_{k2},\dots,X_{kn}), k=1,2,\dots,m$ ,k=1,2,…,m，向量
$(X_{i1},X_{i2},\dots,X_{in})$ 　　与
$(X_{j1},X_{j2},\dots,X_{jn})$ 间的斯皮尔曼等级相关系数公式为：　　
$\rho=1-\frac{6\sum\limits_{k=1}^m{d_k^2}}{n(n^2-1)}$ 　　式中
$d$ 为
$X_{i}$ 、
$X_{j}$ 的秩次差平方。　　根据【图表1】中学生成绩表计算第3名和第5名学生成绩之间的斯皮尔曼秩相关系数。　　解：第3名成绩向量为A(76,93,93,79,71,27)、第5名成绩向量为B(80,39,48,75,41,52)，斯皮尔曼秩相关系数计算表如下，

图表3：将向量A从大到小排序，排序后向量A中的76其序位为4，秩次为4。向量A中有2个93，秩次为1和2。在向量B，中，80的秩次为1,39的秩次为6 　　
$\rho=1-\frac{6\sum\limits_{k=1}^m{d_k^2}}{n(n^2-1)}=1-\frac{6\times 48}{6(6^2-1)}=-0.37143$ 　　三、肯德尔秩相关系数（Kendall Rank Correlation）　　肯德尔秩相关系数是一个用来测量两个随机变量相关性的统计值。一个肯德尔检验是一个无参数假设检验，它使用计算而得的相关系数去检验两个随机变量的统计依赖性。肯德尔相关系数的取值范围在-1到1之间，当肯德尔相关系数为1时，表示两个随机变量拥有一致的等级相关性；当肯德尔相关系数为-1时，表示两个随机变量拥有完全相反的等级相关性；当肯德尔相关系数为0时，表示两个随机变量是相互独立的。　　设有m个n维向量
$(X_{k1},X_{k2},\dots,X_{kn}), k=1,2,\dots,m$ ,k=1,2,…,m，向量
$(X_{i1},X_{i2},\dots,X_{in})$ 　　与
$(X_{j1},X_{j2},\dots,X_{jn})$ 间的肯德尔秩相关系数：　　
$\tau=\frac{2P}{\frac{1}{2}n(n-1)}-1=\frac{4P}{n(n-1)}-1$ 　　式中
$P$ 为
$X_{i}$ 对
$X_{j}$ 或
$X_{j}$ 对
$X_{i}$ 的秩次贡献之和。对
$P$ 值的理解参见下例：　　设有8名学生身高和体重统计数据如下表，

　　计算肯德尔秩相关系数。　　解、通常情况下，人的身高和体重呈正比例关系，先将升高样本按大到小排序，

　　对身高排序后可以看出身高最高者体重不是最重者，但是身材高者体重总体来说还是较重的，为进一步体现两者关系，计算两者的秩次和体重的秩次贡献，数据如下表：

　　表中A学生身材最高（秩次为1），体重排名为3（秩次为1），在A学生后面所有其他学生体重中，A学生体重超过5个人，取贡献
$P_1=5$ 。A学生身材最高，他的体重完全贡献分应该能达到7分。　　B学生身材第二高（秩次为2），体重排名为4（秩次为4），在B学生后面所有其他学生体重中，B学生体重超过4个人，取贡献
$P_2=4$ 。其他学生体重贡献得分同理。　　体重贡献和：
$P=5+4+5+4+3+1+0+0=22$ 。肯德尔秩相关系数为，　　
$\tau=\frac{2P}{\frac{1}{2}n(n-1)}-1=\frac{4P}{n(n-1)}-1=\frac{4\times 22}{8(8-1)}-1\approx 0.5714$ 　　四、余弦相似度(Cosine Similarity) 　　几何中夹角余弦可用来衡量两个向量方向的差异，机器学习中用这一概念来衡量样本向量之间的差异。夹角余弦的取值范围为[-1,1]。夹角余弦越大表示两个向量的夹角越小，夹角余弦越小表示两向量的夹角越大。当两个向量的方向重合时夹角余弦取最大值1，当两个向量的方向完全相反夹角余弦取最小值-1。　　设有m个n维向量
$(X_{k1},X_{k2},\dots,X_{kn}), k=1,2,\dots,m$ ,k=1,2,…,m，向量
$(X_{i1},X_{i2},\dots,X_{in})$ 　　与
$(X_{j1},X_{j2},\dots,X_{jn})$ 间的余弦相似度：　　
$\cos(\theta)=\frac{\sum\limits_{k=1}^nX_{ik}\times X_{jk}}{\sqrt{\sum\limits_{k=1}^nX_{ik}^2\times\sum\limits_{k=1}^nX_{jk}^2}}$ 　　根据附表I中学生成绩表计算第3名和第5名学生成绩之间的余弦相似度。　　解：第3名成绩向量为A(76,93,93,79,71,27)、第5名成绩向量为B(80,39,48,75,41,52)，两者余弦相似度为，　　
$\sum\limits_{k=1}^6X_{ik}\times X_{jk}=76\times 80+93\times 39+93\times 48+79\times 75+71\times 41+27\times 52=24411$ 　　
$\sum\limits_{k=1}^6X_{ik}^2=76^2+93^2+93^2+79^2+71^2+27^2=35085$ 　　
$\sum\limits_{k=1}^6X_{jk}^2=80^2+39^2+48^2+75^2+41^2+52^2=20235$ 　　
$\cos(\theta)=\frac{\sum\limits_{k=1}^6X_{ik}\times X_{jk}}{\sqrt{\sum\limits_{k=1}^6X_{ik}^2\times\sum\limits_{k=1}^6X_{jk}^2}}=\frac{24411}{\sqrt{35085\times 20235}}=0.916164$ 　　余弦相似度和前面几种相似度方法区别是：两组样本趋同时，余弦相似度趋近于0，其它方法则趋近于1。　　各种相似性方法的取值范围都是[-1，1]，计算值趋于1表示高度“相似”、计算值趋于-1表示高度“相异”。　　各种“距离”和“相似性”方法中，欧氏距离是最常见的距离度量，而余弦相似度则是最常见的相似度度量，很多的距离度量和相似度度量都是基于这两者的变形和衍生。　　从计算角度可，马氏距离计算量较大，通常将数据采取标准化（中心化）处理后运用欧氏距离即可替代。原因是结果中心化处理的数据协方差很小，可以忽略不计

jaccard相似性系数_相似性系数的计算公式

相关推荐