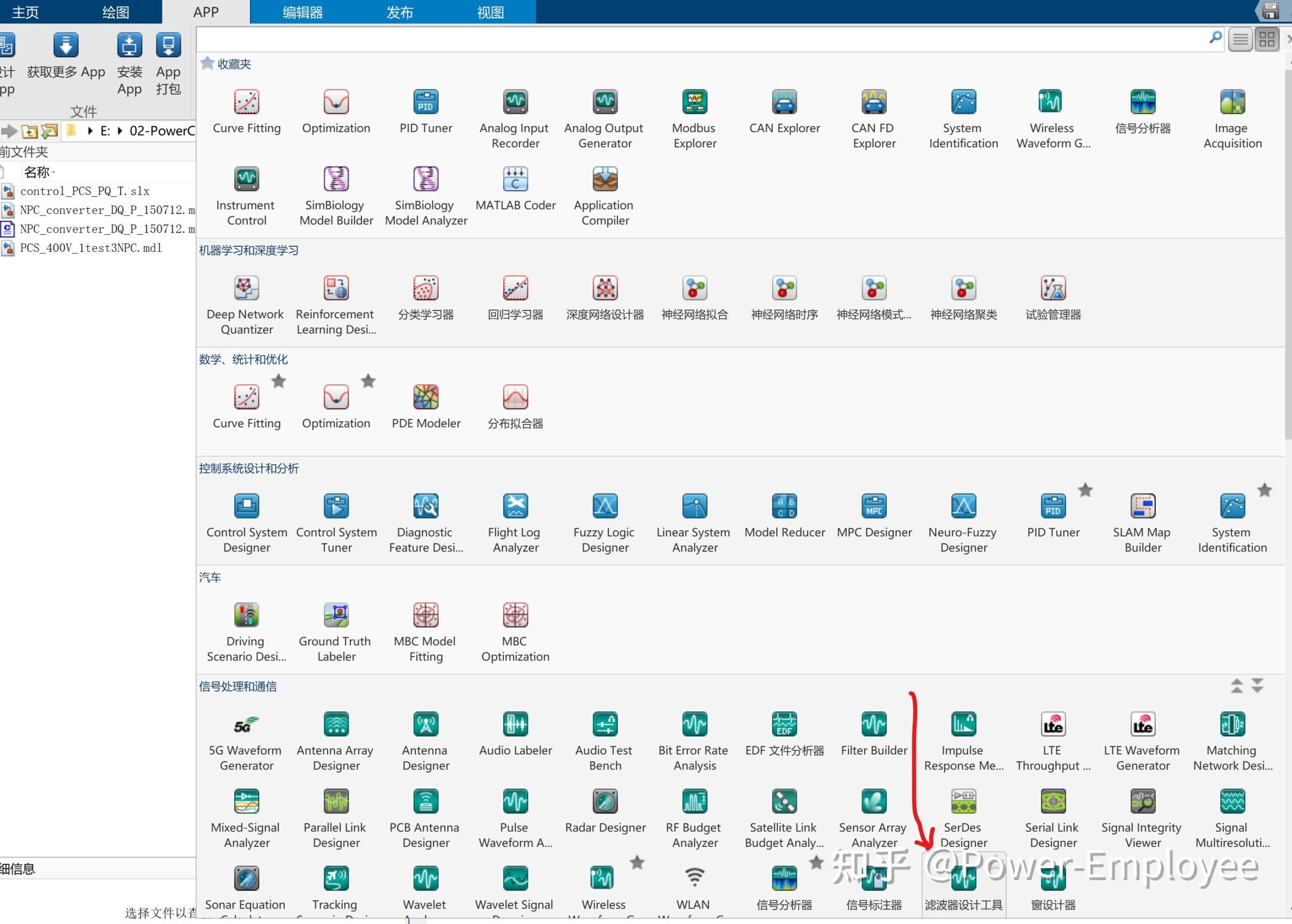
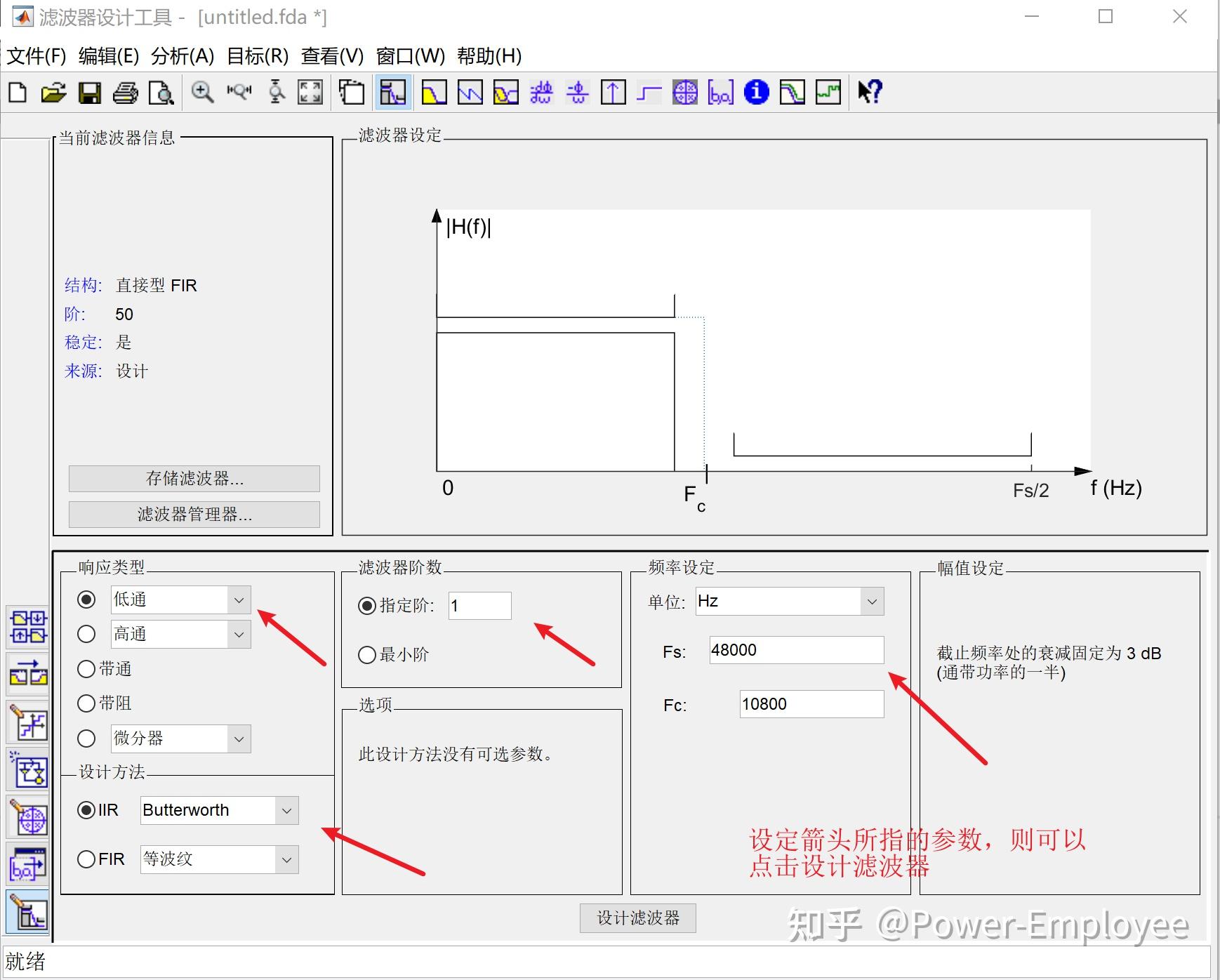
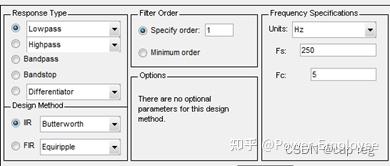
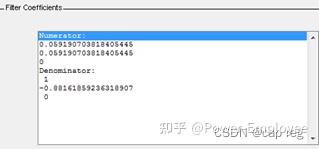
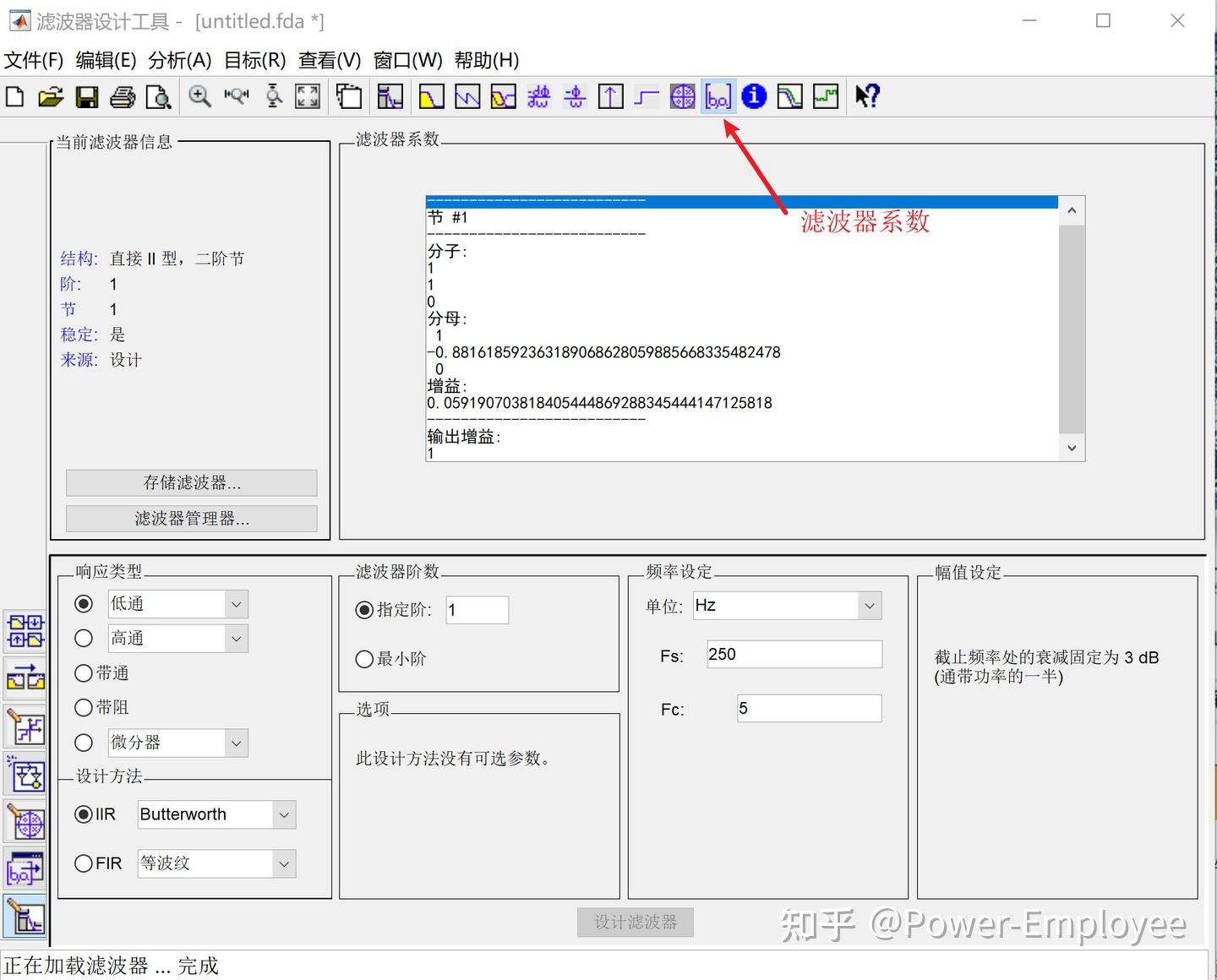
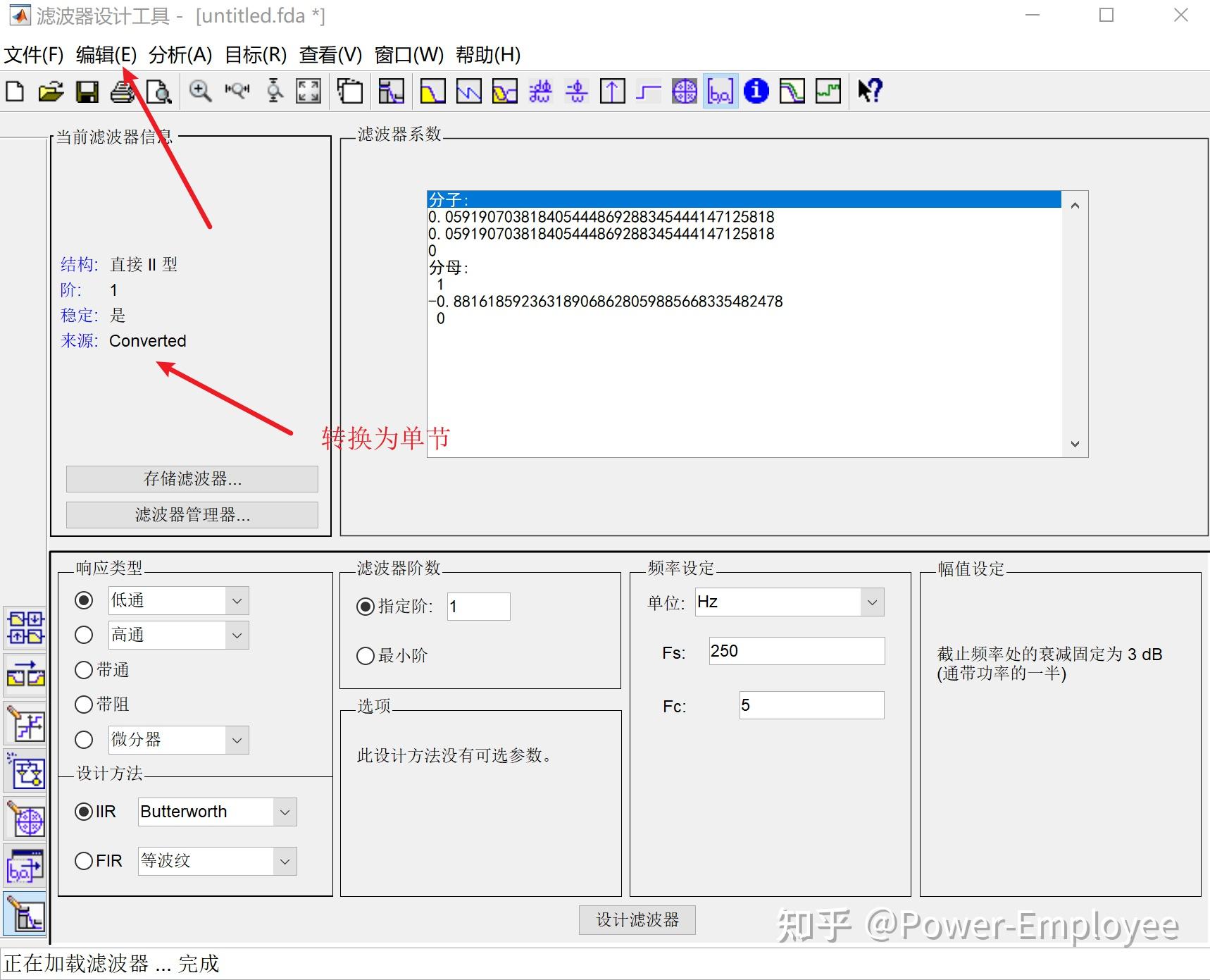
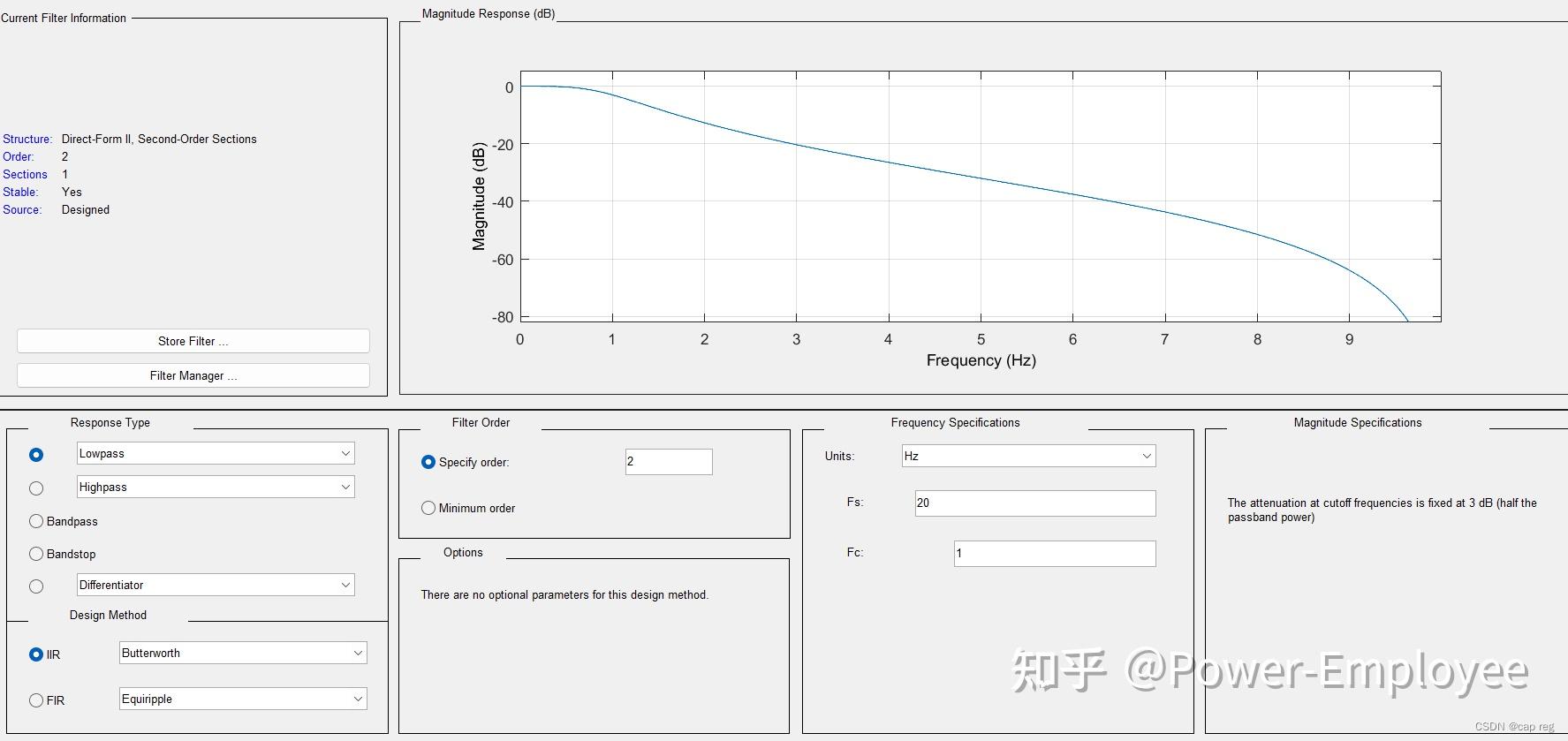
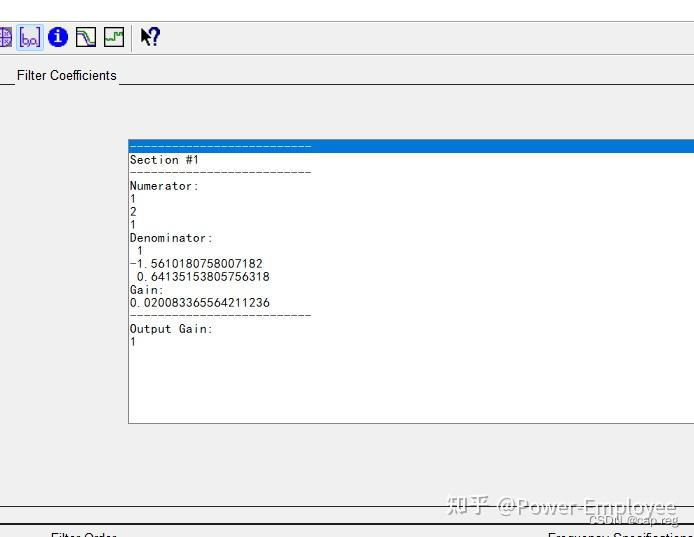
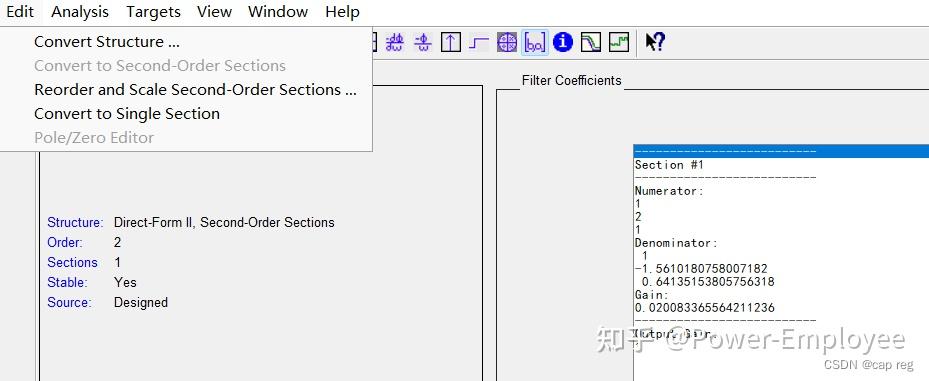
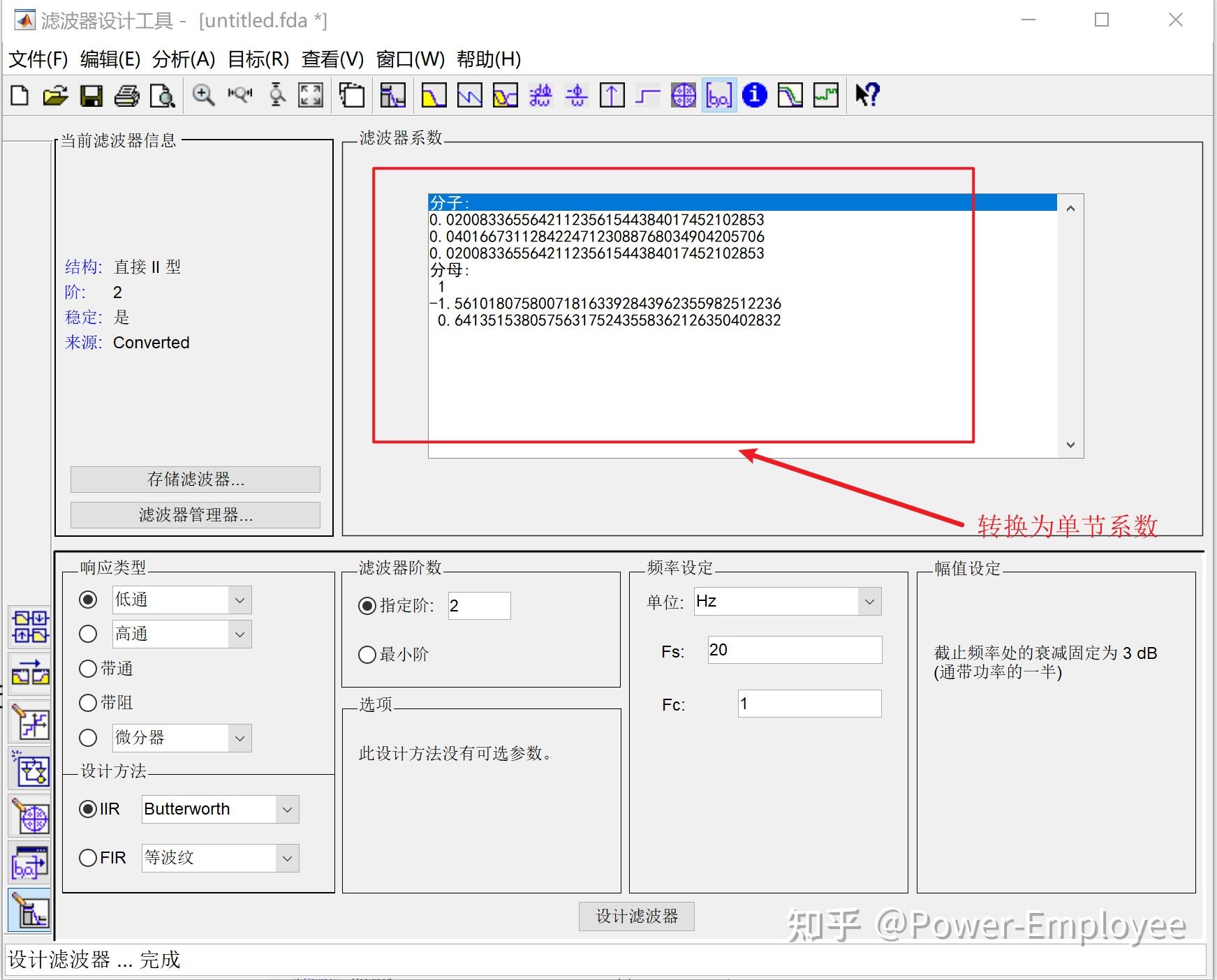
二阶低通巴特沃斯滤波系数(工程实现) 概述 工程常用滤波器通常为一阶或二阶,常用的滤波RC滤波,或均值滤波等。巴特沃斯滤波器因为其固有的特性经常用于信号提取,常用工控、图像和通信。 巴特沃斯滤波器的特点是通频带内的频率响应曲线最大限度平坦,没有起伏,而在阻频带则逐渐下降为零。 Matlab 设计滤波器 一阶巴特沃斯滤波设计 第一步:其参数A和B的求取可以通过Matlab的滤波器工具箱。 步骤:打开Matlab软件,依次Start(在Matlab界面的左下角)->Toolboxes->Filter Design->Filter Design & Analysis Tool (fdatool),打开的界面如下:(老版本英文版本)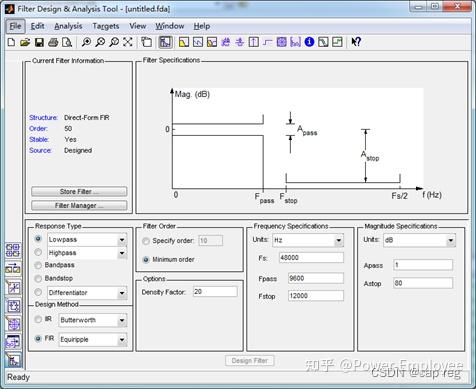

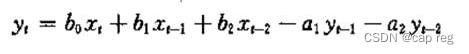


2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/63427.html