判断括号是否匹配的算法_实现两种括号的匹配判断

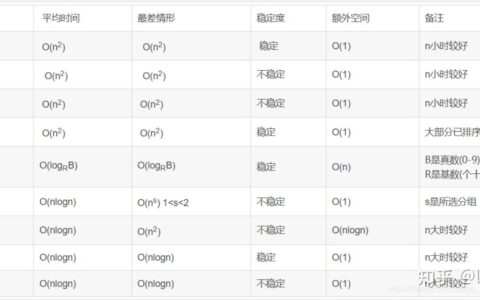
常言道「算法才是编程的灵魂」，不管是 Java，python，还是 PHP，都跨不过算法这个门 　　王国维先生在《人间词话》中写道：古今之成大事业、大学问者，必经过三种境界：“昨夜西风凋碧树。独上高楼，望尽天涯路。”此第一境也。“衣带渐宽终不悔，为伊消得人憔悴。”此第二境也。“众里寻他千百度，蓦然回首，那人却在，灯火阑珊处。”此第三境也。算法的学习之道也是如此。 　　一、夯实基础 　　在最初的阶段，算法世界的大门刚刚打开，这个时候迷茫是正常的，解决迷茫的要诀在于少想多做，勇往直前。怀着一颗”千磨万击还坚韧，任尔东西南北风”的恒心，爬上算法的高楼，做到”望尽天涯路”。 　　从一个算法萌新入门，第一步便在于打牢根基。推荐阅读书籍： 　　1.《算法第 4 版》- Robert Sedgewick 　　适合初学者入门 　　2.《大话数据结构》- 程杰 　　3.《算法图解》- Aditya Bhargava 　　《大话数据结构》和《算法图解》这两本书的特点是有趣、易理解，也非常适合初学者。 　　4.《数据结构和算法分析- C 语言描述》- Mark Allen Weiss 　　需要有一定 C 语言基础 　　进阶： 　　1.《编程珠玑》- Jon Bentley 　　本书讨论了程序设计人员面对一系列的实践问题以及处理问题的措施（处理计划的代码以 C/C++ 言语编写）。书当选取了许多具有典型意义的复杂编程和算法问题，并论述和总结了许多共同精妙的设计准绳、考虑和处理问题的办法以及适用的程序设计技巧。 　　2.《算法导论》- Cormen,T.H. 　　《算法导论》的特点是全面，它是一本算法的百科全书，着重在于开阔算法视野，适合有一定算法基础后再去学习。 　　入门阶段是看一些天赋的，花费时间因人而异，大约在 3～6 月之间，将上述提到的书籍选择其中一本看完基本就能入门了。在这个阶段中，需要了解几类常用的算法： 　　1. 常用的数据结构：数组、字符串、链表、树（如二叉树）等 　　2. 常用的算法：分治、贪心、穷举、动态规划、回溯、二分算法、深度优先搜索等 　　可搭配力扣的题目进行练习
算法思维导图 　　其中，暴力枚举、贪心算法容易理解，可以很快上手。数论相关的算法需求用到一些数学技巧，包括位运算、幂函数、求模等等性质。二分算法和深度优先搜索算法相对有些技巧性，好在他们都有固定的模板。另外，不得不提的是，深度优先搜索算法的思想非常重要，而且深度优先搜索是动态规划、分治和回溯的基础，需求重点控制。 　　在此过程中，可以辅以力扣（LeetCode）中的简单标题，它们常常都代表了一类经典算法，如： 　　70. 爬楼梯假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 　　每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？ 　　动态规划 算法的经典题目，通过此题目可以了解状态、边界条件、状态转移方程等基本概念。 　　112. 路径总和给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。 　　深度优先算法 的入门题目，递归实现和迭代实现都不难，可以学习到深度优先算法的层层嵌套搜索、找到答案或到达边界停止的基本解题思路。 　　35. 搜索插入位置给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。 　　二分算法 的典型题目，使用二分算法的解题模板可以轻松解决，二分算法的算法思想清晰明确，一通百通。 　　169. 求众数给定一个大小为 n 的数组，找到其中的众数。众数是指在数组中出现次数大于 的素。 　　你可以假设数组是非空的，并且给定的数组总是存在众数。 　　分治算法 的简单题目，如果我们知道数组左边一半和右边一半的众数，我们就可以用线性时间知道全局的众数是哪个。这道题妙就妙在可以有多种解题方式，让初学者至少可以写出暴力枚举算法 AC 题目，然后再逐步深入，优化算法。 　　944. 删列造序给定由 N 个小写字母字符串组成的数组 A，其中每个字符串长度相等。 　　选取一个删除索引序列，对于 A 中的每个字符串，删除对应每个索引处的字符。 所余下的字符串行从上往下读形成列。 　　假设，我们选择了一组删除索引 ，那么在执行删除操作之后， 中所剩余的每一列都必须是 非降序 排列的，然后请你返回 的最小可能值。 　　这是一道 贪心算法 的简单题目，贪心算法理解简单，上手容易，适合作为初学者掌握的第一个算法。 　　时间充裕的同学可以按照下图进行系统性地学习： 　　
　　二、融会贯通 　　学习算法理论如同阅读了一本武功秘籍，然而仅仅掌握理论是不够的，接下来就要进入到实际练习阶段。 　　实战练习非常重要，不经过实战练习，理论仅仅是纸上谈兵。比如，不经过大量练习，永远不会知道二分算法是多么容易出现死循环。一个边界条件控制不好，程序就会显示无情的”Time Limit Exceeded”。在 20 分钟的调试后，或许仅仅是将 while (left <= right) 改为了 while (left < right) 。程序员说到底也是手艺人，这一个字符的改动，正是”台上一分钟，台下十年功”的体现，需要在大量的练习中才能理解两者之间的不同作用。 　　再比如，动态规划算法中，递归的函数就像是《盗梦空间》中的”梦中梦”，一层套一层，又渐次展开，很难整体把控。在不断的练习后，才会知道，动态规划算法的重点是抓住动态转移方程，只处理两个状态之间的过渡和边界条件，慢慢”大事化小，小事化了”。 　　
　　这一阶段花费的时间将会很长很长，伴随着不断地摔倒、爬起，你会对每类算法逐渐融会贯通。好在这一阶段是不看天赋只看勤奋的，每次从坑里爬起，都是献给成长的一份力量。 　　推荐的进阶书籍有《编程珠玑》，本书探讨了程序设计人员面对一系列的实际问题以及解决问题的措施（解决方案的代码以 C/C++ 语言编写）。书中选取了许多具有典型意义的复杂编程和算法问题，并阐述和总结了许多独特精妙的设计原则、思考和解决问题的方法以及实用的程序设计技巧。 　　在这个阶段，可以尝试练习力扣上的中等题目，中等题目基本上也只会使用一种算法，加上一些特殊的限制，好比让你在学习了直拳的理论后衍生出左勾拳和右勾拳。推荐练习题目有： 　　1048. 最长字符串链给出一个单词列表，其中每个单词都由小写英文字母组成。 　　如果我们可以在 word1 的任何地方添加一个字母使其变成 word2，那么我们认为 word1 是 word2 的前身。例如，”abc” 是 “abac” 的前身。 　　词链是单词 [word_1, word_2, …, word_k] 组成的序列，k >= 1，其中 word_1 是 word_2 的前身，word_2 是 word_3 的前身，依此类推。 　　从给定单词列表 words 中选择单词组成词链，返回词链的最长可能长度。 　　分析题目可知，要求出答案必须遍历所有可能的词链，动态规划算法在其中起备忘录的作用，用于记录已经算过的答案，减少计算次数。 　　47. 全排列 II给定一个可包含重复数字的序列，返回所有不重复的全排列。 　　这道题是 46. 全排列 的加强版，全排列 I 的题目是：给定一个 没有重复 数字的序列，返回其所有可能的全排列。使用深度优先搜索算法即可解决。本题在其基础上加强了难度，有两种方法可解。第一种方法最简单，直接用全排列 I 的答案去重即可，第二种方法是先将数组排序，全排列时遇到重复数字则跳过，这样的剪枝优化可以减少遍历次数，提高算法效率。 　　40. 组合总和 II给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。 　　candidates 中的每个数字在每个组合中只能使用一次。 　　深度优先搜索算法衍生出来的回溯算法，同样用到 47 题的剪枝优化思想：相同数字只允许递归第一个。 　　89. 格雷编码格雷编码是一个二进制数字系统，在该系统中，两个连续的数值仅有一个位数的差异。 　　给定一个代表编码总位数的非负整数 n，打印其格雷编码序列。格雷编码序列必须以 0 开头。 　　动态规划 算法的实际应用之一。 　　79. 单词搜索给定一个二维网格和一个单词，找出该单词是否存在于网格中。 　　单词必须按照字母顺序，通过相邻的单格内的字母构成，其中“相邻”单格是那些水平相邻或垂直相邻的单格。同一个单格内的字母不允许被重复使用。 　　深度优先搜索的中级应用，使用单独数组标记已使用过的素，这也是 DFS 中较为常见的做法，难点在于将标记数组复原的时机，需要反复练习，熟练掌握。 　　当你把每一类算法的中等题目刷起来得心应手时，不妨开始尝试困难题目的练习。困难题目总是融合两种或两种以上算法，或是加深难度的经典算法，如二维甚至三维动态规划。练习困难题目好比同时用上左勾拳和扫堂腿，不仅让思维酣畅淋漓，在每次 AC 之后还会带来无与伦比的成就感。推荐练习题目有： 　　679. 24 点游戏你有 4 张写有 1 到 9 数字的牌。你需要判断是否能通过 ，，，，， 的运算得到 24。 　　只有 4 张牌，且只能执行 4 种操作。即使所有运算符都不进行交换，最多也只有 12 * 6 * 2 * 4 * 4 * 4 = 9216 种可能性，这使得我们可以尝试所有这些可能，如果用深度优先搜索算法则需要费一番功夫。 　　124. 二叉树中的最大路径和给定一个非空二叉树，返回其最大路径和。 　　本题中，路径被定义为一条从树中任意节点出发，达到任意节点的序列。该路径至少包含一个节点，且不一定经过根节点。 　　首先，考虑实现一个简化的函数：计算每个节点及其子树对路径和的最大贡献。再考虑第二点：最大路径不一定包括根节点。这意味着我们在每一步都检查哪种选择更好：是继续当前路径或者以当前节点作为最高节点计算新的路径。 　　410. 分割数组的最大值给定一个非负整数数组和一个整数 m，你需要将这个数组分成 m 个非空的连续子数组。设计一个算法使得这 m 个子数组各自和的最大值最小。 　　二分算法和贪心算法的综合练习，仔细分析可知其单调关系：数组和的最大值越小，分组数越大。并且数组和的范围是可以确定的。根据此特性，可以将题目转换为：当子数组的和最大为 maxSum 时，至少需要分多少组，能否在最多 m 组的限制范围内完成分割。在每次分割时，采用贪心策略，尽可能多的放置素，直到一组放不下，再另起一组。如果满足分割条件，记录当前值，利用二分法，缩小子数组总和。否则扩大子数组总和，直到找到最佳答案。 　　三、推陈出新 　　事实上，大量程序员停留在第二重境界就无法再进一步。当提到某一类算法时，你可以说：”我知道”、”我会用”、”踩过坑”，但能说出”我完全理解其思想”、甚至”我能想办法改进”的人却很少很少。这一步仿佛武学中的攻守之道，当你掌握到这一层，便可不再拘泥于一刀一剑、一招一式，如金书中所说：飞花摘叶皆可伤人、草木竹石均可为剑。 　　开创算法的过程是艰难又孤独的。每一个经典算法的诞生都伴随着”一将功成万骨枯”。比如现在我们在很多语言中都可以直接调用实现快速排序，而在快速排序算法出现之前，曾有一段时间仅有冒泡、选择、插入三种排序算法。直到1959年，希尔提出”希尔排序”算法，或许现在知道此算法的人已经很少了。但它是首个突破了复杂度的排序算法，它的基本算法思想如下：选择一个增量序列t1，t2，…，tk，其中 ti > tj， tk = 1； 按增量序列个数k，对序列进行k 趟排序； 每趟排序，根据对应的增量ti，将待排序列分割成若干长度为 m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。 　　动图演示如下：
　　希尔排序算法较为晦涩难懂，而且并不是最优的排序算法，现在已经被后来的快速排序算法给淘汰了。然而不可否认希尔对排序算法的演进具有开创性贡献，在攀越算法高峰的路上，每一步都走得战战兢兢，我们只有铭记这些伟大的引路人，以此激励自己不断前行。 　　算法世界不尽完美。不仅有经典算法在前奠基，后起之秀遗传算法、深度学习算法也熠熠生辉。算法世界还有许多”所罗门王的宝藏”，一直静静地守候在”灯火阑珊处”，等待着人们去发掘。 　　四、学习方法 　　我给大家整理了一个学习计划，可以保存下图进行学习：
　　现在网上有很多资源、博客、论坛可供我们更方便地学习知识片段。然而这种类似兵来将挡、水来土掩般的学习方法虽然有用，却并不特别的好。这里推荐大家在网上寻找一些系统的学习教程，以帮助自己由浅入深，一路成长。 　　五、真题演练 　　力扣将   里比较新的题目按照类别进行了整理，以供大家按模块练习。 　　模拟 　　134. 加油站 　　146. LRU缓存机制 　　202. 快乐数 　　289. 生命游戏 　　371. 两整数之和 　　412. Fizz Buzz 　　数组 　　152. 乘积最大子序列 　　169. 求众数 　　189. 旋转数组 　　217. 存在重复素 　　283. 移动零 　　384. 打乱数组 　　350. 两个数组的交集 II 　　334. 递增的三子序列 　　240. 搜索二维矩阵 II 　　238. 除自身以外数组的乘积 　　链表 　　138. 复制带随机指针的链表 　　141. 环形链表 　　148. 排序链表 　　160. 相交链表 　　206. 反转链表 　　234. 回文链表 　　237. 删除链表中的节点 　　328. 奇偶链表 　　堆 　　155. 最小栈 　　215. 数组中的第K个最大素 　　295. 数据流的中位数 　　378. 有序矩阵中第K小的素 　　347. 前K个高频素 　　栈 　　150. 逆波兰表达式求值 　　227. 基本计算器 II 　　341. 扁平化嵌套列表迭代器 　　哈希 / Map 　　171. Excel表列序号 　　454. 四数相加 II 　　380. 常数时间插入、删除和随机素 　　队列 　　239. 滑动窗口最大值 　　树 　　230. 二叉搜索树中第K小的素 　　236. 二叉树的最近公共祖先 　　297. 二叉树的序列化与反序列化 　　线段树 　　218. 天际线问题 　　排序 　　179. 最大数 　　324. 摆动排序 II 　　二分检索 　　162. 寻找峰值 　　287. 寻找重复数 　　315. 计算右侧小于当前素的个数 　　滑动窗口 　　395. 至少有K个重复字符的最长子串 　　动态规划 　　124. 二叉树中的最大路径和 　　128. 最长连续序列 　　198. 打家劫舍 　　279. 完全平方数 　　300. 最长上升子序列 　　322. 零钱兑换 　　329. 矩阵中的最长递增路径 　　图论 　　127. 单词接龙 　　200. 岛屿的个数 　　207. 课程表 　　210. 课程表 II 　　数学 & 位运算 　　136. 只出现一次的数字 　　149. 直线上最多的点数 　　166. 分数到小数 　　172. 阶乘后的零 　　190. 颠倒二进制位 　　191. 位1的个数 　　204. 计数质数 　　268. 缺失数字 　　326. 3的幂 　　字符串 　　125. 验证回文串 　　131. 分割回文串 　　139. 单词拆分 　　140. 单词拆分 II 　　208. 实现 Trie (前缀树) 　　212. 单词搜索 II 　　242. 有效的字母异位词 　　387. 字符串中的第一个唯一字符 　　344. 反转字符串 　　最后呢，这里希望各位小伙伴们都能够学有所成，这里呢 准备了些福利给大家。 　　

　　这个图书学习路径出自，leecode 全站第一 的人之手  。什么？看书枯燥？来看视频课程吧。

　　资料下载地址：https://www.code0.cn 　　课程目标：深入掌握java高级数据结构，写出高品质代码，突破技术瓶颈 　　数据结构与算法—-课程大纲 　　开篇词：算法是进入IT名企的钥匙 　　第一部分：数据结构 　　一 数据结构基础 　　1.1什么是数据结构 　　1.2基本概念和术语 　　1.3抽象数据类型的表示与实现 　　1.4算法和算法分析 　　1.4.1算法 　　1.4.2算法设计的要求 　　1.4.3算法的时间复杂度度量与空间复杂度度量 　　1.4.4算法的存储空间需求 　　二 线性表 　　2.1线性表的类型定义 　　2.2线性表的业务结构 　　2.3 ArrayList类的完整实现 　　2.4线性表的链式表示和实现 　　2.5LinkedList单链表类的实现 　　2.7循环单链表实现 　　2.8双向链表实现 　　2.9双向环链表实现 　　2.10 大数乘法的数组与链表实战 　　2.11数组排序 　　2.11.1选择排序与性能分析优化 　　2.11.2冒泡排序与性能分析优化 　　2.11.3希尔排序与性能分析优化 　　2.11.4插入排序与性能分析优化 　　2.11.5二分查找插入排序与性能分析优化 　　2.11.6归并排序与性能分析优化 　　2.11.7快速排序与性能分析优化 　　2.11.8奇偶排序与性能分析优化 　　2.11.9基数排序与性能分析优化 　　2.11.10木桶排序与性能分析优化 　　2.11.11归并排序与性能分析优化 　　2.11.12鸡尾酒排序与性能分析优化 　　2.11.13地精排序与性能分析优化 　　2.11.14堆排序与性能分析优化 　　2.11.15锦标赛排序与性能分析优化 　　2.11.16梳子排序与性能分析优化 　　2.12查找 　　2.12.1无序查找 　　2.12.2有序查找 　　2.12.3.1 二分查找 　　2.12.3.2 中值查找 　　2.12.3.3 斐波那契查找 　　2.12.3.4 三分查找 　　2.12.3.5 二分查找近似查找 　　2.13链表排序 　　2.13.1链表插入排序 　　2.13.2链表选择排序 　　2.13.3链表冒泡排序 　　2.13.4链表快速排序 　　2.13.5链表归并排序 　　2.14数组与链表时空效率比较 　　三 哈希表与集合 　　3.1哈希函数 　　3.2哈希碰撞 　　3.3哈希表数组实现 　　3.4哈希表链表实现 　　3.5集合概念 　　3.6交集，并集，差集 　　3.7数组集合 　　3.8链表集合 　　3.9哈希集合 　　3.10哈希表用于数据查找 　　3.11集合用于数据处理 　　四 栈和队列 　　4.1栈 　　4.1.1抽象数据类型栈的定义 　　4.1.2栈的表示和实现 　　4.1.2.1 数组栈 　　4.1.2.2 正向链式栈 　　4.1.2.3 反向链式栈 　　4.2栈的应用举例 　　4.2.1数制转换 　　4.2.2括号匹配的检验 　　4.2.3行编辑程序 　　4.2.4迷宫求解 　　4.2.5表达式求值 　　4.2.6汉诺塔 　　4.3栈与递归的实现 　　4.4队列 　　4.4.1抽象数据类型队列的定义 　　4.4.2链队列——队列的数组表示和实现 　　4.4.3链队列——队列的链式表示和实现 　　4.4.4循环队列——队列的数组表示和实现 　　4.4.5双端队列——队列的数组表示和实现 　　4.4.6双端队列——队列的链表表示和实现 　　4.4.7优先队列初步——队列的数组表示和实现 　　4.4.8优先队列初步——队列的链表表示和实现 　　4.5离散事件模拟 　　4.6用栈模拟递归 　　4.7用队列模拟递归 　　4.8树状文件夹遍历 　　4.9栈的用途 　　4.10队列的用途 　　五 字符串 　　5.1 串及串匹配 　　5.2 蛮力算法 　　5.3 KMP算法 　　5.4 BM算法 　　5.5 Karp-Rabin算法 　　5.6字符串实现高精度加法 　　5.7字符串实现高精度减法 　　5.8字符串实现高精度乘法 　　5.9字符串实现高精度除法 　　5.10AC自动机 　　5.11分词与SIM哈希 　　六   数组和矩阵 　　6.1 数组 　　6.1.1 抽象数据类型 　　6.1.2 不规则二维数组 　　6.1.3 数组嵌套 　　6.2 矩阵 　　6.2.1 定义和操作 　　6.2.2 类matrix 　　6.3 特殊矩阵 　　6.3.1 定义和应用 　　6.3.2 对角矩阵 　　6.3.3 三对角矩阵 　　6.3.4 三角矩阵 　　6.3.5 对称矩阵 　　6.4 特殊矩阵与稀疏矩阵 　　6.4.1 基本概念 　　6.4.2 用单个线性表描述 　　6.4.3 用多个线性表描述 　　6.4.4 性能测量 　　6.4.5矩阵的压缩存储 　　6.5广义表的定义 　　6.6广义表的存储结构 　　6.7m多项式的表示 　　6.8广义表的递归算法 　　6.8.1求广义表的深度 　　6.8.2复制广义表 　　6.8.3建立广义表的存储结构 　　七  树和二叉树 　　7.1树的定义和基本术语 　　7.2二叉树 　　7.2.1二叉树的定义 　　7.2.2二叉树的性质 　　7.2.3二叉树的存储结构 　　7.2.4二叉树的实现 　　7.3遍历二叉树和线索二叉树 　　7.3.1遍历二叉树 　　7.3.2线索二叉树 　　7.4树和森林 　　7.4.1树的存储结构 　　7.4.2森林与二叉树的转换 　　7.4.3树和森林的遍历 　　7.5树与等价问题 　　7.6编码树，Huffman树及其应用 　　7.7.1最优二叉树（Huffman树） 　　7.7.2Huffman编码实现压缩解压缩 　　7.7回溯法与树的遍历 　　7.8树的计数 　　八 平衡搜索树 　　8.1 AVL树 　　8.1.1 定义 　　8.1.2 AVL树的高度 　　8.1.3 AVL树的描述 　　8.1.4 AVL搜索树的搜索 　　8.1.5 AVL搜索树的插入 　　8.1.6 AVL搜索树的删除 　　8.2 红-黑树 　　8.2.1 基本概念 　　8.2.2 红-黑树的描述 　　8.2.3 红-黑树的搜索 　　8.2.4 红-黑树的插入 　　8.2.5 红-黑树的删除 　　8.2.6 实现细节的考虑及复杂性分析 　　8.3 分裂树 　　8.3.1 介绍 　　8.3.2 分裂树的操作 　　8.3.3 折算复杂性 　　8.4 B-树 　　8.4.1 索引顺序访问方法 　　8.4.2 m叉搜索树 　　8.4.3 m阶B-树 　　8.4.4 B-树的高度 　　8.4.5 B-树的搜索 　　8.4.6 B-树的插入 　　8.4.7 B-树的删除 　　8.4.8 节点结构 　　九  图 　　9.1 基本概念 　　9.2 应用和更多的概念 　　9.3 特性 　　9.4 抽象数据类型graph 　　9.5 无权图的描述 　　9.5.1 邻接矩阵 　　9.5.2 邻接链表 　　9.5.3 邻接数组 　　9.6 加权图的描述 　　9.7 类实现 　　9.7.1 不同的类 　　9.7.2 邻接矩阵类 　　9.7.3 扩充chain类 　　9.7.4 链表类 　　9.8 图的遍历 　　9.8.1 广度优先搜索 　　9.8.2 广度优先搜索的实现 　　9.8.3 方法graph:bfs的复杂性分析 　　9.8.4 深度优先搜索 　　9.8.5 深度优先搜索的实现 　　9.8.6 方法graph:dfs的复杂性分析 　　9.9 应用 　　9.9.1 寻找一条路径Dijskra算法 　　9.9.2 连通图及其构成 　　9.9.3 最小生成树，普里姆算法，克鲁斯卡尔算法 BottleNeck算法，MstReducePrim算法，SecondaryMst算法 　　9.9.4 最短路径 A*算法  floyd算法 Dijskra算法  Bellman算法，SPFA算法，JohnSon算法 　　9.9.5拓扑排序 　　9.10  网络流 　　9.10.1　流网络 　　9.10.2　FordFulkerson方法 　　9.10.3　最大二分匹配 　　9.10.4　推送重贴标签算法 　　9.10.5　前置重贴标签算法 　　9.11拓扑排序 　　9.12欧拉回路 　　9.13DAG有向无环图 　　第10天 跳表和字典 　　10.1 字典 　　10.2 抽象数据类型 　　10.3 线性表描述 　　10.4 跳表表示（可选） 　　10.4.1 理想情况 　　10.4.2 插入和删除 　　10.4.3 级的分配 　　10.4.4 结构skipNode 　　10.4.5 类skipList 　　10.4.6 skipList方法的复杂度 　　十一  bitmap与布隆过滤器 　　11.1位运算快速回顾与bitset实现 　　11.2 bitmap实战 　　11.3 布隆过滤器实现 　　十二  外部排序 　　12.1外存信息的存取 　　12.2外部排序的方法 　　12.3多路平衡归并的实现 　　12.4置换选择排序 　　12.5最佳归并树 　　十三   文件 　　13.1有关文件的基本概念 　　13.2顺序文件 　　13.3索引文件 　　13.4isam文件和vsam文件 　　13.4.1isam文件 　　13.4.2vsam文件 　　13.5直接存取文件（散列文件） 　　13.6多关键字文件 　　13.6.1多重表文件 　　13.6.2倒排文件 　　十四 优先级队列 　　14.1 定义和应用 　　14.2 抽象数据类型 　　14.3 线性表 　　14.4 堆 　　14.4.1 定义 　　14.4.2 大根堆的插入 　　14.4.3 大根堆的删除 　　14.4.4 大根堆的初始化 　　14.4.5 类maxHeap 　　14.4.6 堆和STL 　　14.5 左高树 　　14.5.1 高度优先与宽度优先的最大及最小左高树 　　14.5.2 最大HBLT的插入 　　14.5.3 最大HBLT的删除 　　14.5.4 两棵最大HBLT的合并 　　14.5.5 初始化 　　14.5.6 类maxHblt 　　14.6 堆延申 　　14.6.1 斐波那契堆 　　14.6.2 Treap 　　14.6.3 pair堆 　　14.6.4 rank-pair堆 　　14.6.5 二项堆 　　14.7 应用 　　14.7.1 堆排序 　　14.7.2 机器调度 　　十五  Java JVM内存回收管理演变 　　15.1概述 　　15.2可利用空间表及分配方法 　　15.3边界标识法 　　15.3.1可利用空间表的结构 　　15.3.2分配算法 　　15.3.3回收算法 　　15.4伙伴系统 　　15.4.1可利用空间表的结构 　　15.4.2分配算法 　　15.4.3回收算法 　　15.5无用单收集 　　15.6存储紧缩 　　十六 竞赛树 　　16.1 赢者树和应用 　　16.2 抽象数据类型WinnerTree 　　16.3 赢者树的实现 　　16.3.1 表示 　　16.3.2 赢者树的初始化 　　16.3.3 重新组织比赛 　　16.3.4 类completeWinnerTree 　　16.4 输者树 　　16.5 应用 　　16.5.1 用最先适配法求解箱子装载问题 　　16.5.2 用相邻适配法求解箱子装载问题 　　第17章 高级树 　　17.1  伸展树 　　17.2  B+树 　　17.3  2-3树 　　17.4  kd-树 　　17.5  树堆 　　17.6  散列树 　　17.7 topTree 　　17.8 笛卡尔树 　　17.9 T树 　　17.10 Dancing Tree 　　17.11 前缀树后缀树基数树 　　17.12 R树 线段树 　　17.13 区间树 　　17.14PQ树 　　17.15 VEB树 　　17.16  Link-cut tree与Cover tree 　　17.17 并查集 　　第二部分：算法 　　一  数学基础 　　1.1 函数增长与复杂性分类 　　1.1.1 渐进符号 　　1.1.2 阶的计算 　　1.1.3 复杂性分类 　　1.2 概率论 　　1.2.1 事件与概率 　　1.2.2 期望与方差 　　1.3 代数学 　　1.3.1 矩阵 　　1.3.2 行列式 　　1.3.3 解线性方程组 　　1.3.4 多项式 　　1.1.5 复数 　　1.1.6 群 　　1.4 组合学 　　1.4.1 排列与组合 　　1.4.2 鸽巢原理 　　1.4.3 容斥原理 　　1.4.4 特殊计数序列 　　1.4.5 Pólya计数定理 　　1.5 博弈论 　　1.5.1 博弈树 　　1.5.2 SG函数 　　1.5.3 Nim游戏与Nim 　　1.6 数论 　　1.6.1 整除 　　1.6.2 不定方程 　　1.6.3 同余方程与欧拉定理 　　1.6.4 原根、离散对数和二项同余方程 　　1.6.5 连分数 　　二  初等数论与组合数学 　　2.1 整除 　　2.2 质数与合数 　　2.3 质数筛法 　　2.4 质因数分解 　　2.5 最大公约数和最小公倍数 　　2.6 模运算 　　2.7 同余 　　2.8 欧几里得算法 　　2.9 扩展欧几里得算法 　　2.10 模意义下的乘法逆 　　2.11 与质数有关的定理 　　2.12 线性同余方程 　　2.13 中国剩余定理 　　2.14基本计数原理 　　2.15 排列 　　2.16 组合 　　2.17 杨辉三角 　　2.18 特殊排列组合 　　2.19     stirling数 　　2.20 Catalan数 　　2.21 容斥原理 　　2.22 鸽巢原理 　　三 暴力求解法 　　3.1 简单枚举 　　3.2 枚举排列 　　3.2.1 生成1~n的排列 　　3.2.2 生成可重集的排列 　　3.2.3 解答树 　　3.2.4 下一个排列 　　3.3 子集生成 　　3.3.1 增量构造法 　　3.3.2 位向量法 　　3.3.3 二进制法 　　3.4 回溯法 　　3.4.1 八皇后问题 　　3.4.2 其他应用举例 　　3.5 路径寻找问题 　　3.6 迭代加深搜索 　　四　数论算法 　　4.1　基础数论概念 　　4.2　最大公约数 　　4.3　模运算 　　4.4　求解模线性方程 　　4.5　中国余数定理 　　4.6　素的幂 　　4.7　RSA公钥加密系统 　　4.8　素数的测试 　　4.9　整数的因子分解 　　五　概率分析和随机算法 　　5.1　雇用问题 　　5.2　指示器随机变量 　　5.3　随机算法 　　5.4　概率分析和指示器随机变量的进一步使用 　　5.4.1　生日悖论 　　5.4.2　球与箱子 　　5.4.3　特征序列 　　5.4.4　在线雇用问题 　　六 贪婪算法 　　6.1 最优化问题 　　6.2 贪婪算法思想 　　6.3 应用 　　6.3.1 货箱装载 　　6.3.2 0/1背包问题 　　6.3.3 拓扑排序 　　6.3.4 二分覆盖 　　6.3.5 单源最短路径 　　6.3.6 最小成本生成树 　　6.3.7赫夫曼编码 　　6.3.8　拟阵和贪心算法 　　6.3.9　用拟阵求解任务调度问题 　　七  分而治之 　　7.1 算法思想 　　7.2 应用 　　7.2.1 残缺棋盘 　　7.2.2 归并排序 　　7.2.3 快速排序 　　7.2.4 选择 　　7.2.5 相距最近的点对 　　7.3 解递归方程 　　7.4 复杂度的下限 　　7.4.1 最小最大问题的下限 　　7.4.2 排序算法的下限 　　7.4.3　最大子数组问题 　　7.4.4　矩阵乘法的Strassen算法 　　7.4.5 用代入法求解递归式 　　7.4.5　用递归树方法求解递归式 　　7.4.6　用主方法求解递归式 　　7.4.7　证明主定理 　　7.4.8　对b的幂证明主定理 　　7.4.9  向下取整和向上取整 　　八 动态规划 　　8.1 算法思想 　　8.2 应用 　　8.2.1 0/1背包问题 　　8.2.2 矩阵乘法链 　　8.2.3 所有顶点对之间的最短路径 　　8.2.4 带有负值的单源最短路径 　　8.2.5 网组的无交叉子集 　　8.2.6　钢条切割 　　8.2.7　最长公共子序列 　　8.2.8　最优二叉搜索树 　　8.2.9 最大连续子序列和 　　8.2.10 最长不下降子序列（LIS） 　　8.2.11 最长回文子串 　　8.2.12 DAG最长路 　　8.2.13 背包问题 　　九 回溯法 　　9.1 算法思想 　　9.2 应用 　　9.2.1 货箱装载 　　9.2.2 0/1背包问题 　　9.2.3 最大完备子图 　　9.2.4 旅行商问题 　　9.2.5 电路板排列 　　十 分支定界 　　10.1 算法思想 　　10.2 应用 　　10.2.1 货箱装载 　　10.2.2 0/1背包问题 　　10.2.3 最大完备子图 　　10.2.4 旅行商问题 　　10.2.5 电路板排列 　　十一　摊还分析 　　11.1　聚合分析 　　11.2　核算法 　　11.3　势能法 　　11.4　动态表 　　11.4.1　表扩张 　　11.4.2　表扩张和收缩 　　十二　线性规划 　　12.1　标准型和松弛型 　　12.2　将问题表达为线性规划 　　12.3　单纯形算法 　　12.4　对偶性 　　12.5　初始基本可行解 　　十三　多项式与快速傅里叶变换 　　13.1　多项式的表示 　　13.2　DFT与FFT 　　13.3　高效FFT实现 　　十四　计算几何学 　　14.1 多边形 　　14.1.1 计算几何误差修正 　　14.1.2 计算几何点类 　　14.1.3 计算几何线段类 　　14.1.4 多边形类 　　14.1.5 多边形的重心 　　14.1.6 多边形内格点数 　　14.1.7 凸多边形类 　　14.1.8 凸多边形的直径 　　14.1.9 半平面切割多边形 　　14.1.10 半平面交 　　14.1.11 凸多边形交 　　14.1.12 多边形的核 　　14.1.13 凸多边形与直线集交 　　14.2 圆 　　14.2.1 圆与线求交 　　14.2.2 圆与多边形交的面积 　　14.2.3 最小圆覆盖 　　14.2.4 圆与圆求交 　　14.2.5 圆的离散化 　　14.2.6 圆的面积并 　　14.3 三维计算几何 　　14.3.1 三维点类 　　14.3.2 三维直线类 　　14.3.3 三维平面类 　　14.3.4 三维向量旋转 　　14.3.5 长方体表面两点最短距离 　　14.3.6 四面体体积 　　14.3.7 最小球覆盖 　　14.3.8 三维凸包 　　14.4 其他 　　14.4.1 三角形的四心 　　14.4.2 最近点对 　　14.4.3 平面最小曼哈顿距离生成树 　　14.4.4 最大空凸包 　　14.4.5 平面划分 　　十五　NP完全性 　　15.1　多项式时间 　　15.2　多项式时间的验证 　　15.3　NP完全性与可归约性 　　15.4　NP完全性的证明 　　15.5　NP完全问题 　　15.5.1　团问题 　　15.5.2　顶点覆盖问题 　　15.5.3　哈密顿回路问题 　　15.5.4　旅行商问题 　　15.5.5　子集和问题 　　十六　近似算法 　　16.1　顶点覆盖问题 　　16.2　旅行商问题 　　16.2.1　满足三角不等式的旅行商问题 　　16.2.2　一般旅行商问题 　　16.3　集合覆盖问题 　　16.4　随机化和线性规划 　　16.5　子集和问题 　　十七 高级算法专题 　　17.1 爬山法 　　17.2 模拟退火法 　　17.3 遗传算法 　　17.4 粒子群算法 　　17.5 LRU缓存算法 　　17.6 蚂蚁群算法 　　17.7 神经网络算法 　　第三部分：高并发算法 　　一　多线程算法 　　1.1　动态多线程基础 　　1.2　多线程矩阵乘法 　　1.3　多线程归并排序 　　1.4   多线程快速排序 　　1.5  多线程计算递归 　　1.6  多线程粒子群算法 　　1.7  多线程CAS算法 　　二   线程安全数据结构 　　2.1 线程安全 　　2.2 线程安全队列 　　2.3 线程安全数据结构通用范式 　　三  排名，锁，高并发高性能的秒杀实战 　　3.1 并发优先队列排名 　　3.2 锁与秒杀 　　3.3 高并发实现限流计数器法 　　3.4 高并发实现限流漏桶法 　　3.5 高并发实现限流令牌桶 　　四 调度算法 　　4.1优先调度算法 　　4.1.1.先来先服务调度算法（FCFS） 　　4.1.2.短作业(进程)优先调度算法 　　4.2高优先权优先调度算法 　　4.2.1.非抢占式优先权算法 　　4.2.2.抢占式优先权调度算法 　　4.2.3.高响应比优先调度算法 　　4.3 基于时间片的轮转调度算法 　　4.3.1.时间片轮转法 　　4.3.2.多级反馈队列调度算法 　　4.4 circuit-breaker 熔断算法 　　第四部分：分布式数据结构算法 　　一 分布式哈希表 　　二 分布式负载均衡算法 　　轮询法 　　随机法 　　源地址哈希法 　　加权轮询法 　　加权随机法 　　键值范围法 　　最小连接数法 　　最快响应速度法 　　观察模式法 　　三 分布式选举老大算法 　　四  一致性哈希算法 　　五 分布式安全队列 　　六 分布式安全树 　　七 分布式遗传算法 　　八 分布式投票算法 　　九 KNN分类算法的分布式 　　十Ensemble Selection分布式算法 　　十一 raft共识算法 　　十二 paxos共识算法 　　第五部分：推荐算法 　　1推荐算法概述 　　1.1基于流行度的算法 　　1.2协同过滤算法 　　1.2.1用关联算法做协同过滤 　　1.2.2用聚类算法做协同过滤 　　1.2.3用分类算法做协同过滤 　　1.2.4用回归算法做协同过滤 　　1.2.5用矩阵分解做协同过滤 　　1.2.6用神经网络做协同过滤 　　1.2.7用图模型做协同过滤 　　1.2.8用隐语义模型做协同过滤 　　1.3基于内容的算法 　　1.4基于模型的算法 　　1.5基于约束的推荐系统 　　1.6基于邻域的推荐方法 　　1.6.1基于用户的评分预测 　　1.6.2基于用户的分类预测方法 　　1.6.3基于物品的推荐 　　1.7情境感知推荐系统 　　1.5混合算法 　　第六部分密码学算法 　　1.哈希算法 　　2.对称加密算法 　　3.非对称加密算法 　　4.国密算法 　　第七部分：leetcode实战 　　腾讯算法50题 　　1二叉树的最大深度 　　2反转字符串 　　3Nim游戏 　　4反转字符串中的单词 III 　　5删除链表中的节点 　　6只出现一次的数字 　　7反转链表 　　8求众数 　　9回文数 　　10二叉搜索树的最近公共祖先 　　11合并两个有序链表 　　12买卖股票的最佳时机 II 　　13最小栈 　　14买卖股票的最佳时机 　　15 2的幂 　　16 存在重复素 　　17 爬楼梯 　　18 删除排序数组中的重复项 　　19 合并两个有序数组 　　20 最大子序和 　　21 有效的括号 　　22 环形链表 　　23 相交链表 　　24 最长公共前缀 　　25反转整数 　　26 子集 　　27螺旋矩阵 II 　　28 全排列 　　29 二叉搜索树中第K小的素 　　30 除自身以外数组的乘积 　　31格雷编码 　　32排序链表 　　33数组中的第K个最大素 　　34不同路径 　　35盛最多水的容器 　　36二叉树的最近公共祖先 　　37 最接近的三数之和 　　38旋转链表 　　39字符串相乘 　　40搜索旋转排序数组 　　41螺旋矩阵 　　42两数相加 　　43环形链表 II 　　44最长回文子串 　　45三数之和 　　46字符串转整数 (atoi) 　　47合并K个排序链表 　　48LRU缓存机制 　　49二叉树中的最大路径和 　　50约瑟夫环链表