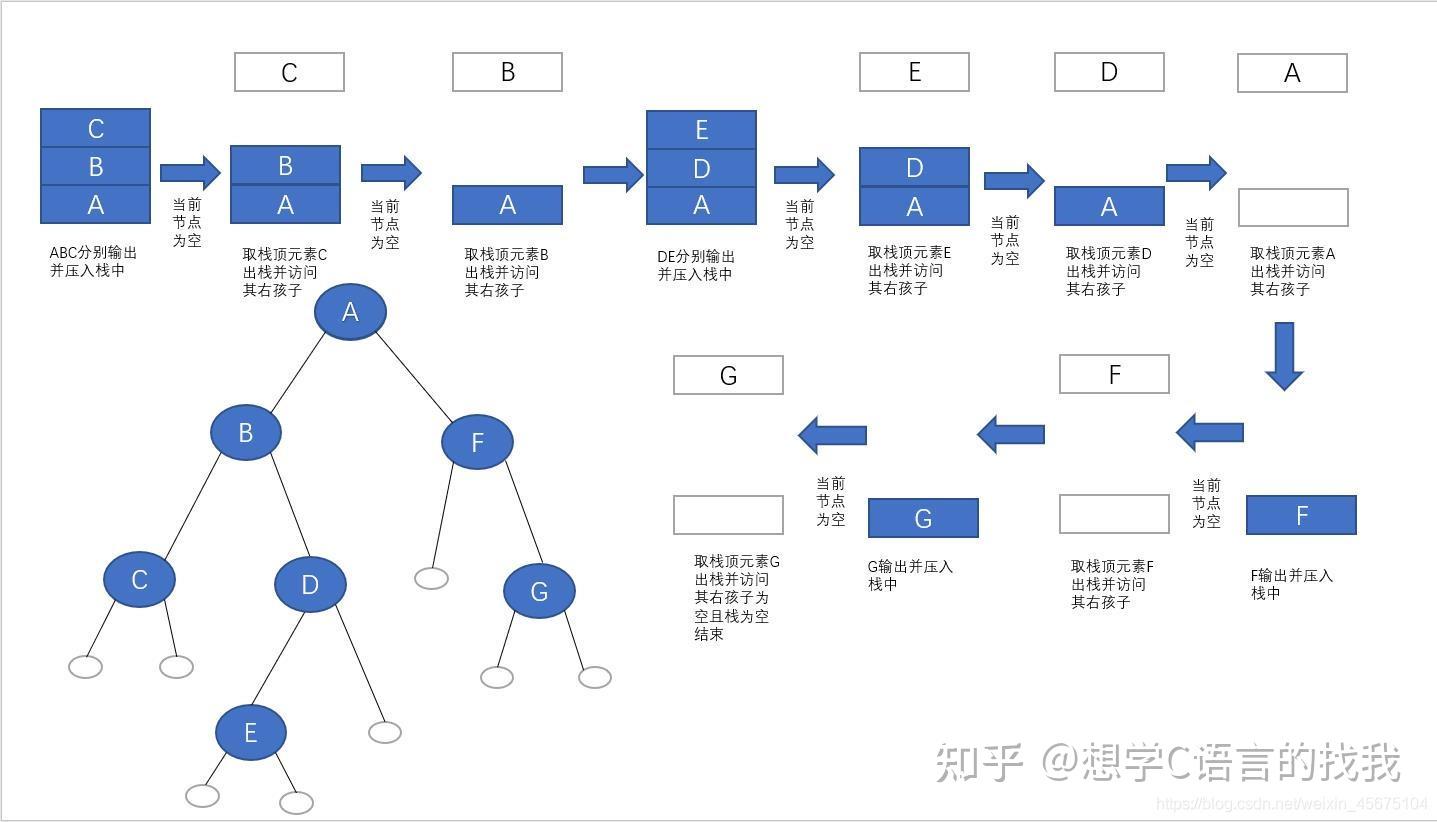
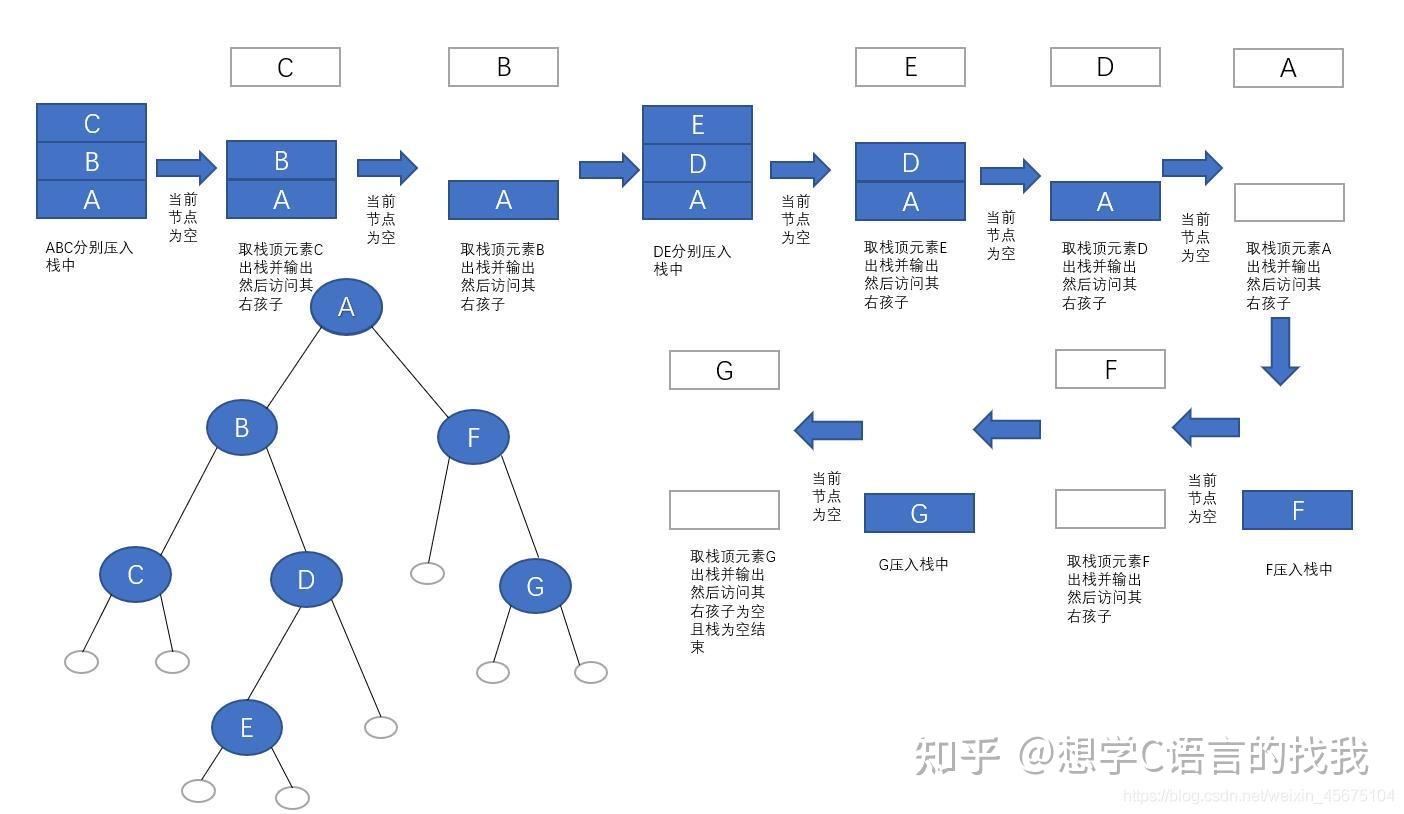
二叉搜索树的后序遍历序列_中序遍历一棵二叉排序数可得到一个二叉树的前序遍历,中序遍历和后序遍历分别有什么作用?先序遍历:在第一次遍历到节点时就执行操作,一般只是想遍历执行操作(或输出结果)可选用先序遍历;中序遍历:对于二分搜索树,中序遍历的操作顺序(或输出结果顺序)是符合从小到大(或从大到小)顺序的,故要遍历输出排序好的结果需要使用中序遍历
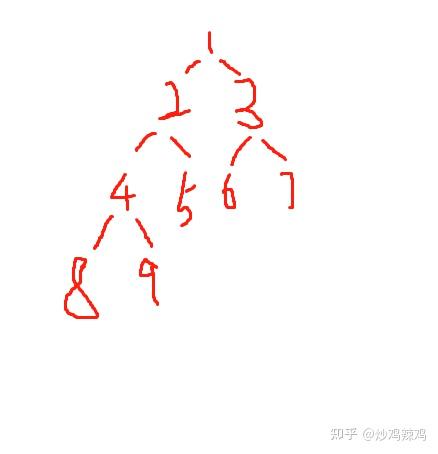
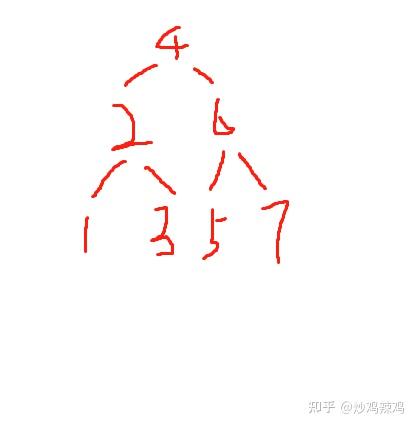
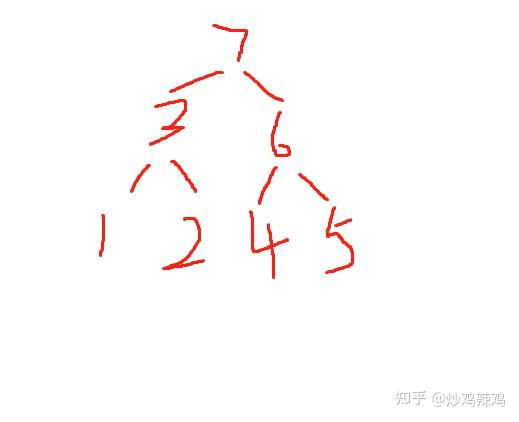
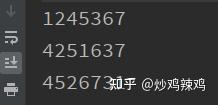
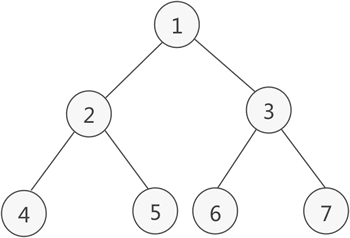
二叉树的前序遍历,中序遍历和后序遍历分别有什么作用? 先序遍历:在第一次遍历到节点时就执行操作,一般只是想遍历执行操作(或输出结果)可选用先序遍历; 中序遍历:对于二分搜索树,中序遍历的操作顺序(或输出结果顺序)是符合从小到大(或从大到小)顺序的,故要遍历输出排序好的结果需要使用中序遍历 后序遍历:后续遍历的特点是执行操作时,肯定已经遍历过该节点的左右子节点,故适用于要进行破坏性操作的情况,比如删除所有节点 什么是二叉树 简单理解为对于一个节点来说,最多拥有一个上级节点,同时最多具备左右两个下级节点的数据结构。 由于很多排序算法都是基于二叉树实现的,多叉树也是二叉树延伸过去的,所以二叉树的建树和遍历就显得非常重要。 二叉树建树 一般情况是给你一个串,要求让你以前序,中序,后序的方式建树。那么此时我们就需要首先了解三个概念:前序遍历中序遍历后序遍历 我们来看看一棵二叉树的结构: 0 / \ 1 2 / \ / \ 3 4 5 60就是整个二叉树的根节点,1就是0这个节点的左子树,2就是0这个节点的右子树。有了这个知识,我们就可以理解前中后序遍历这个位置属性就是指的根在哪个位置,前序遍历就是根在前,所以就是根左子树右子树的遍历方式;中序遍历就是根在中间,所以就是左子树根右子树的遍历方式;后序遍历就是根在最后,所以就是左子树右子树根的遍历方式。 遍历的方式有三种,对应的建树方式有已知中序和前序建树,已知中序和后序建树,已知前序和后序建树三种。如果我们仅仅是想构建一棵二叉平衡树,可以简单使用某一种序列建树。用伪代码表示这三种遍历方式就是前序遍历的方式建树 中序遍历的方式建树 后序遍历的方式建树 前序建树 我们现在以序列 1, 2, 3, 4, 5, 6, 7, 8, 9 为例,如果是前序建树方式,那么二叉树的结构应该为:
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们 举报,一经查实,本站将立刻删除。
文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/57326.html