fft的横坐标_fft输出频谱的横纵坐标

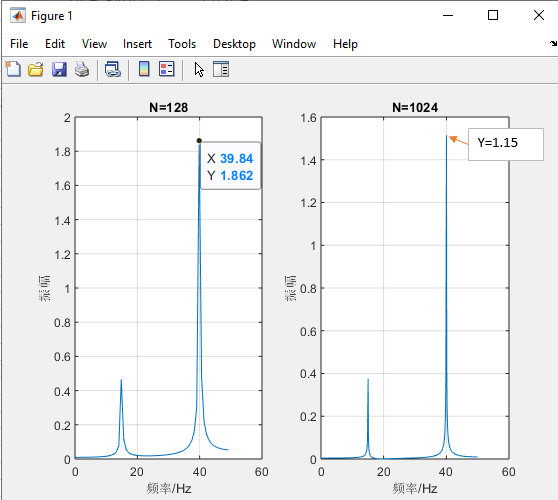
在matlab里面，如何用FFT函数计算出谐波的真实幅值？　　下面的程序是对x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t)做FFT分析，分别在采样点N=128和1024的时候得出的结果如下图，但是都和实际谐波幅值不一样，请问怎样才能求出真实的谐波幅值？　　clf; 　　fs=100;N=128; %采样频率和数据点数　　n=0:N-1;t=n/fs; %时间序列　　x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号就是t=0/100, 1/100, 2/100,…, 126,100, 127/100 　　y=fft(x,N); %对信号进行快速Fourier变换　　mag=abs(y)*2/N; %求得Fourier变换后的振幅　　f=n*fs/N; %频率序列　　subplot(1,2,1),plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅　　xlabel(‘频率/Hz’); 　　ylabel(‘振幅’);title(‘N=128’);grid on; 　　%对信号采样数据为1024点的处理　　fs=100;N=1024;n=0:N-1;t=n/fs; 　　x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); %信号　　y=fft(x,N); %对信号进行快速Fourier变换　　mag=abs(y)*2/N; %求取Fourier变换的振幅　　f=n*fs/N; 　　subplot(1,2,2) 　　plot(f(1:N/2),mag(1:N/2)); %绘出Nyquist频率之前随频率变化的振幅　　xlabel(‘频率/Hz’); 　　ylabel(‘振幅’);title(‘N=1024’);grid on;
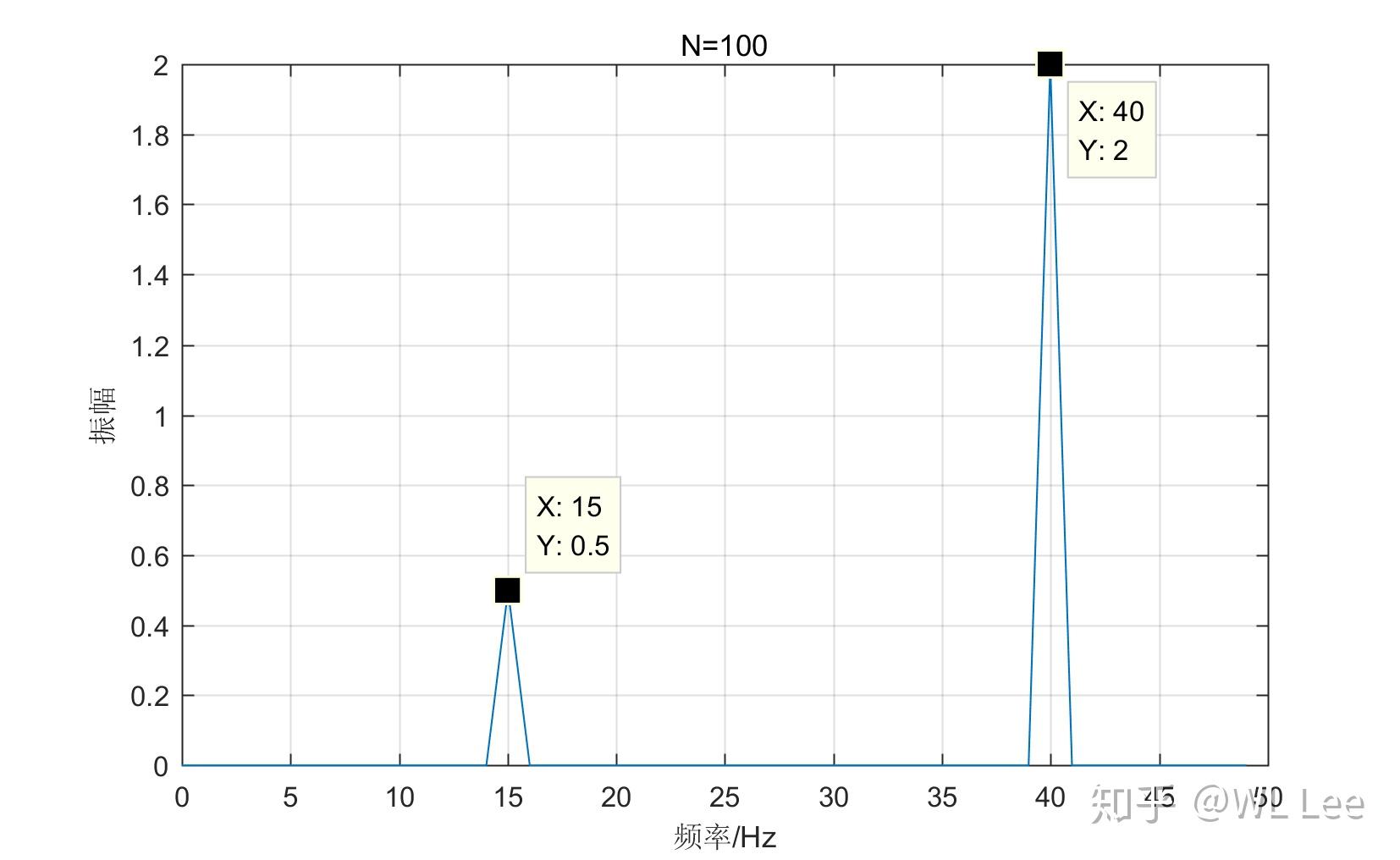
　　泻药。　　之前刚好遇到过这个问题，不是FFT计算的结果幅值不对，而是FFT计算的结果没有信号频率点的幅值，因为信号频率位于两个谱线之间。对于上述问题，可以更改FFT的采样点数，使得信号频率刚好落在谱线上，譬如
　　结果如下:

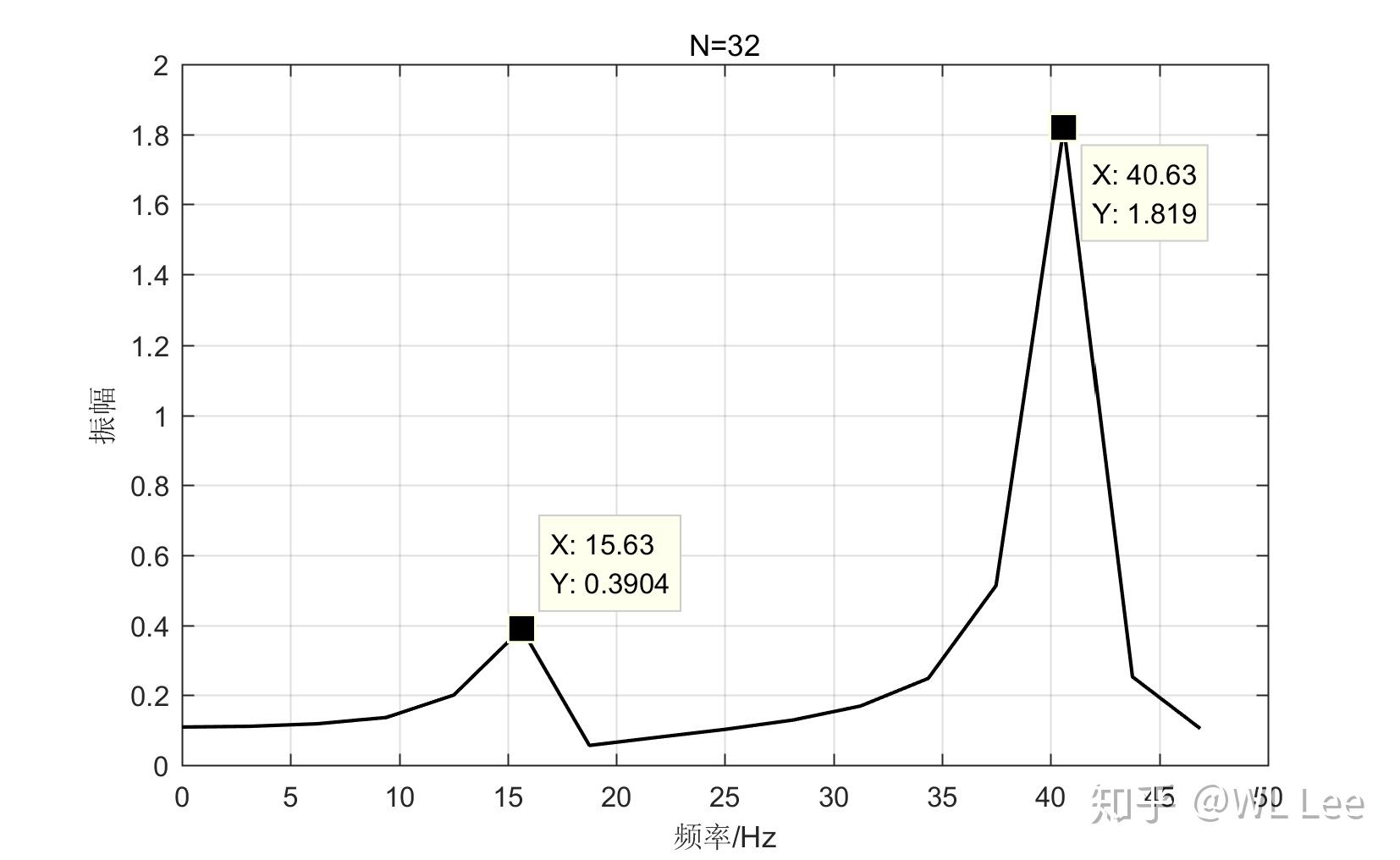
　　当然，真实情况下，信号频率通常是未知的，可以通过一些校正手段来校正FFT计算的峰值。　　依然考虑题主所用的信号，取FFT的采样点数为
(假设不知道信号频率，故取采样点数为2的n次幂加快算法速度) 　　主程序：　　校正函数：　　运行主程序后，先输入谐波个数，然后再用鼠标左键框选出峰值即可

　　校正结果：

　　可以看到，校正结果比直接FFT的结果准确几个量级。具体技术细节可以参考论坛：离散频谱的比值校正法 – MATLAB中文论坛　　虽然理论上二倍的最高信号频率就够了，但是一般采样频率还是五到十倍比较好。如果要精确计算幅值的话首先要对的准，就是采样点正好能落在最高点上，所以别做128或者1024点直接1000点比较好。　　还有你最后，计算幅值是直接abs然后非零频率处乘2就行不是平方。你那是在计算功率　　

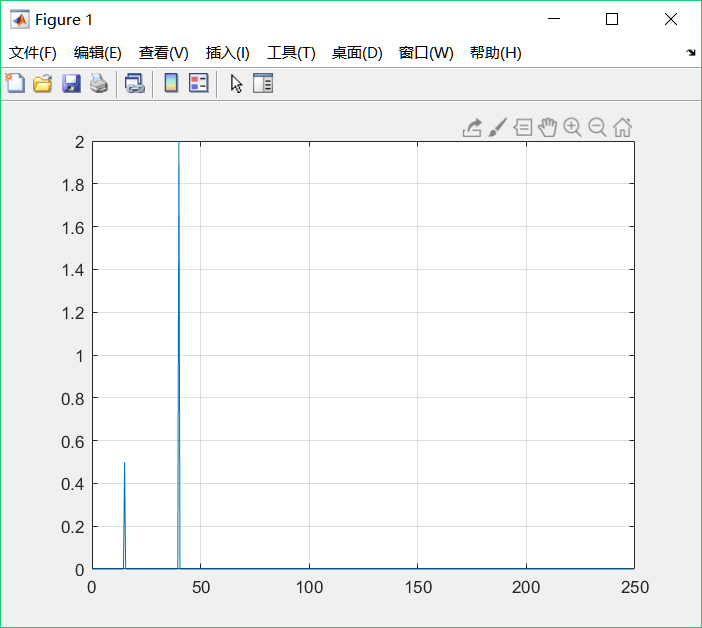
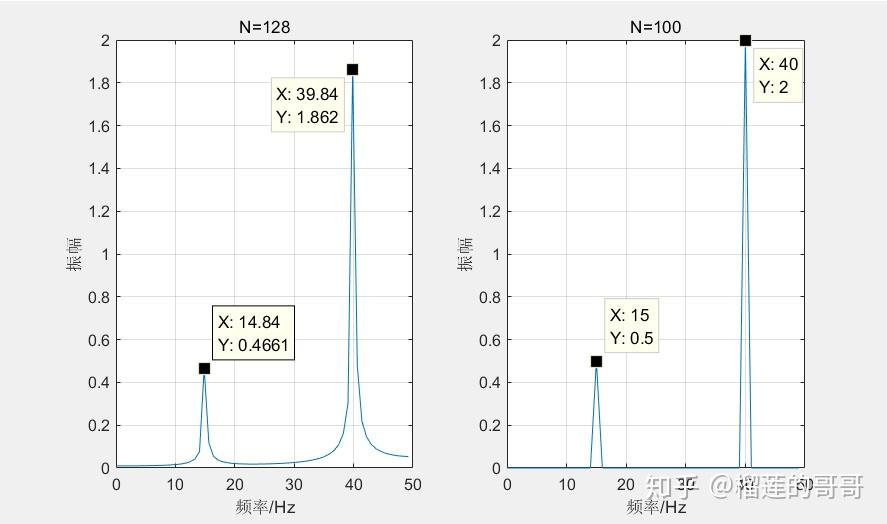
　　根据采样定律你的采样频率取是没错的，工程上一般取5-10倍。你的图像里的幅值和频率不精确，主要是因为出现了频率和幅值泄露的现象。你的采样频率fs是100，也就是说在一秒内你采样了100个点，而你的数据点数N为128、1024，也就是说你在几个采样周期内多出了28个采样点或者24个，而这多出来的点数，经过fft之后不能完全表达出一个采样周期中的频率和幅值，即把剩余的72个或76个点中的幅值和频率给泄露了。　　下图是用你的程序，采用不同数据点数的fft后的对比，左边为128 右边是100。

　　结论：选取的采样点数N 应为采样频率fs 的正整数倍　　细分频率
$\Delta f = \frac{f_s}{N}$ 　　当N=128时，
$\Delta f = 100/128 = 0.78125Hz$ ，15Hz和40Hz都无法被
$\Delta f$ 整除，出现“栅栏效应”——40Hz分量被分散到它的周边频率上，在15Hz分量附近也是同样的现象。另外，为何N=128的图里最高峰处x=39.84，是因为
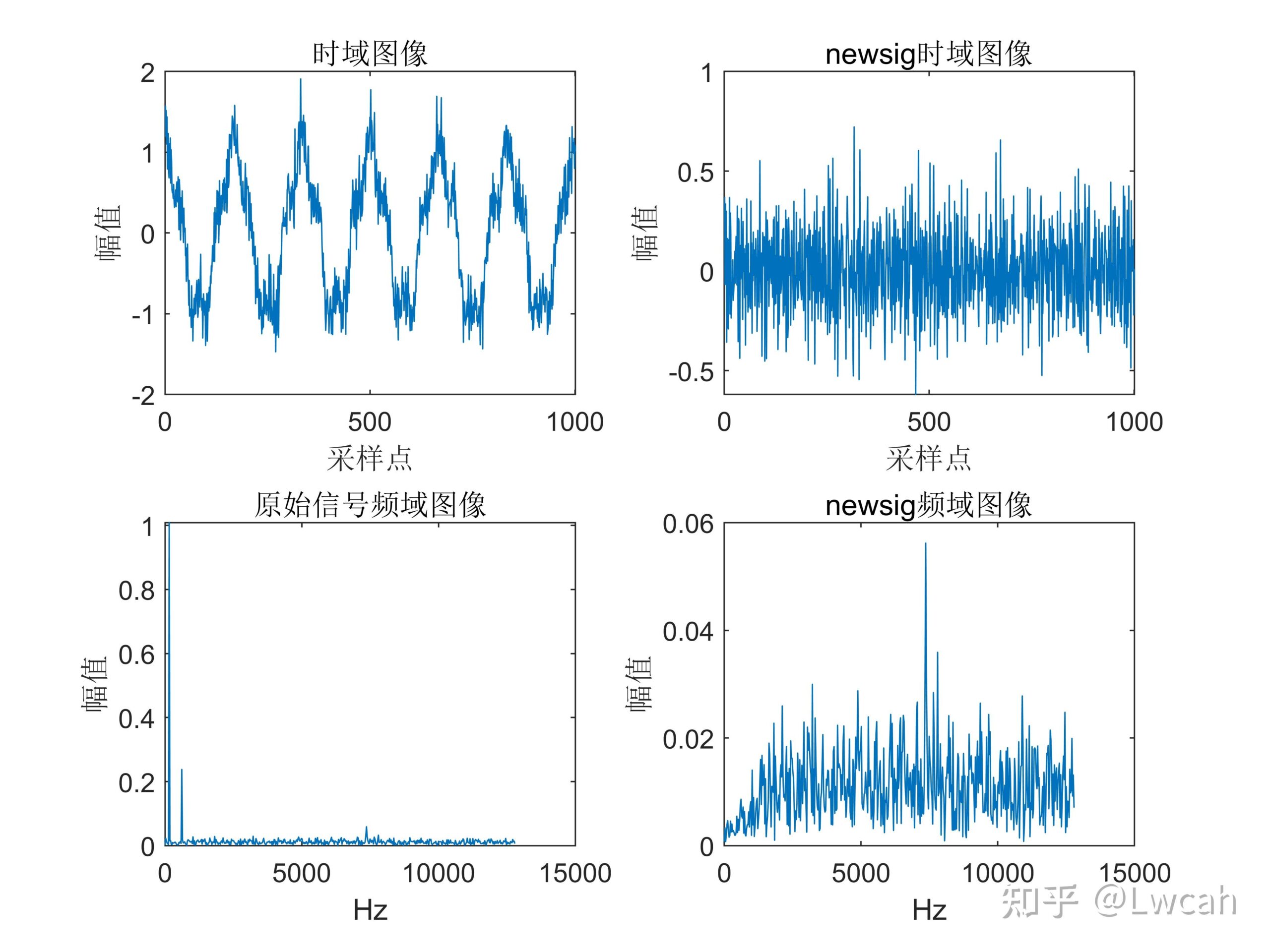
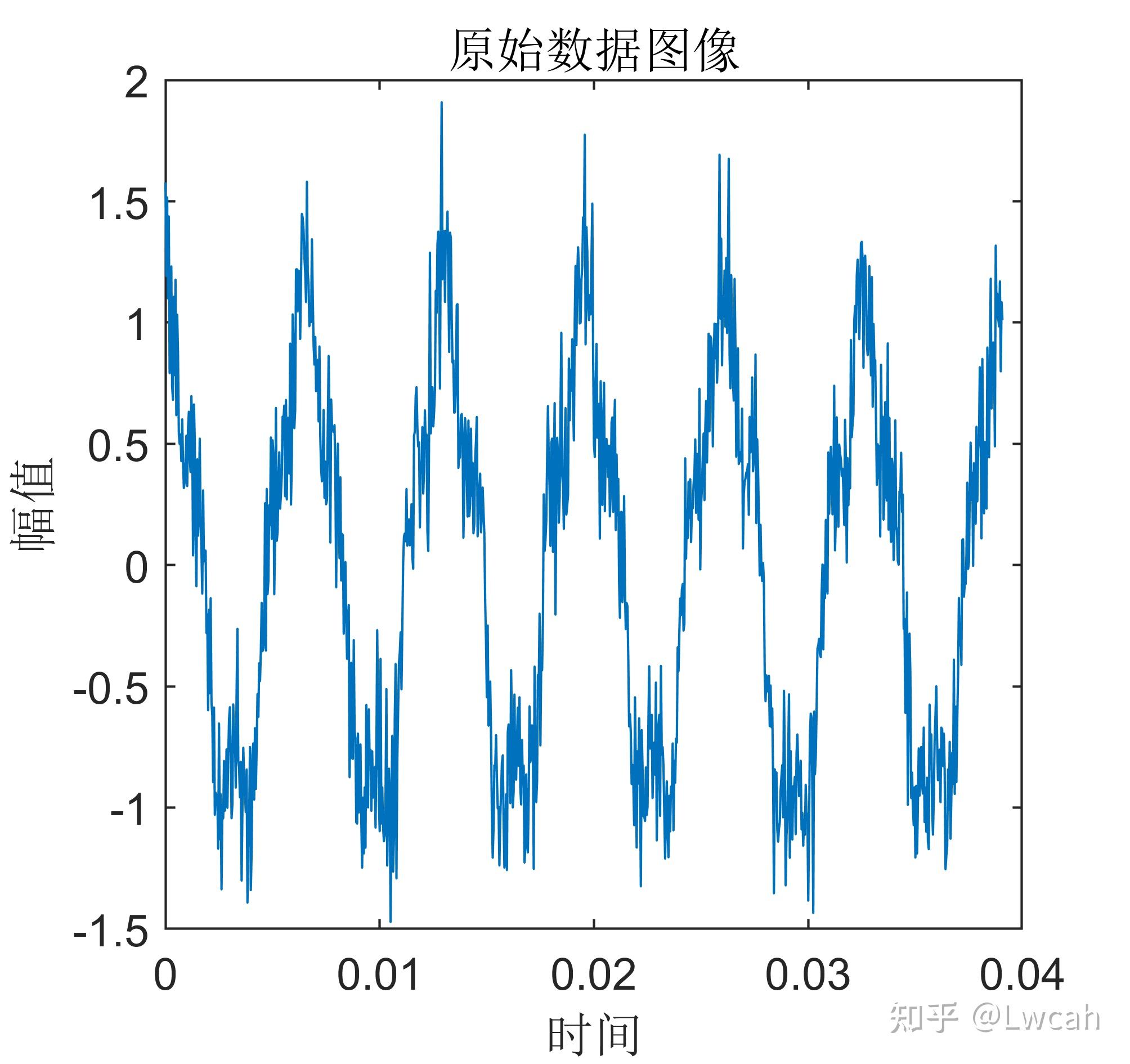
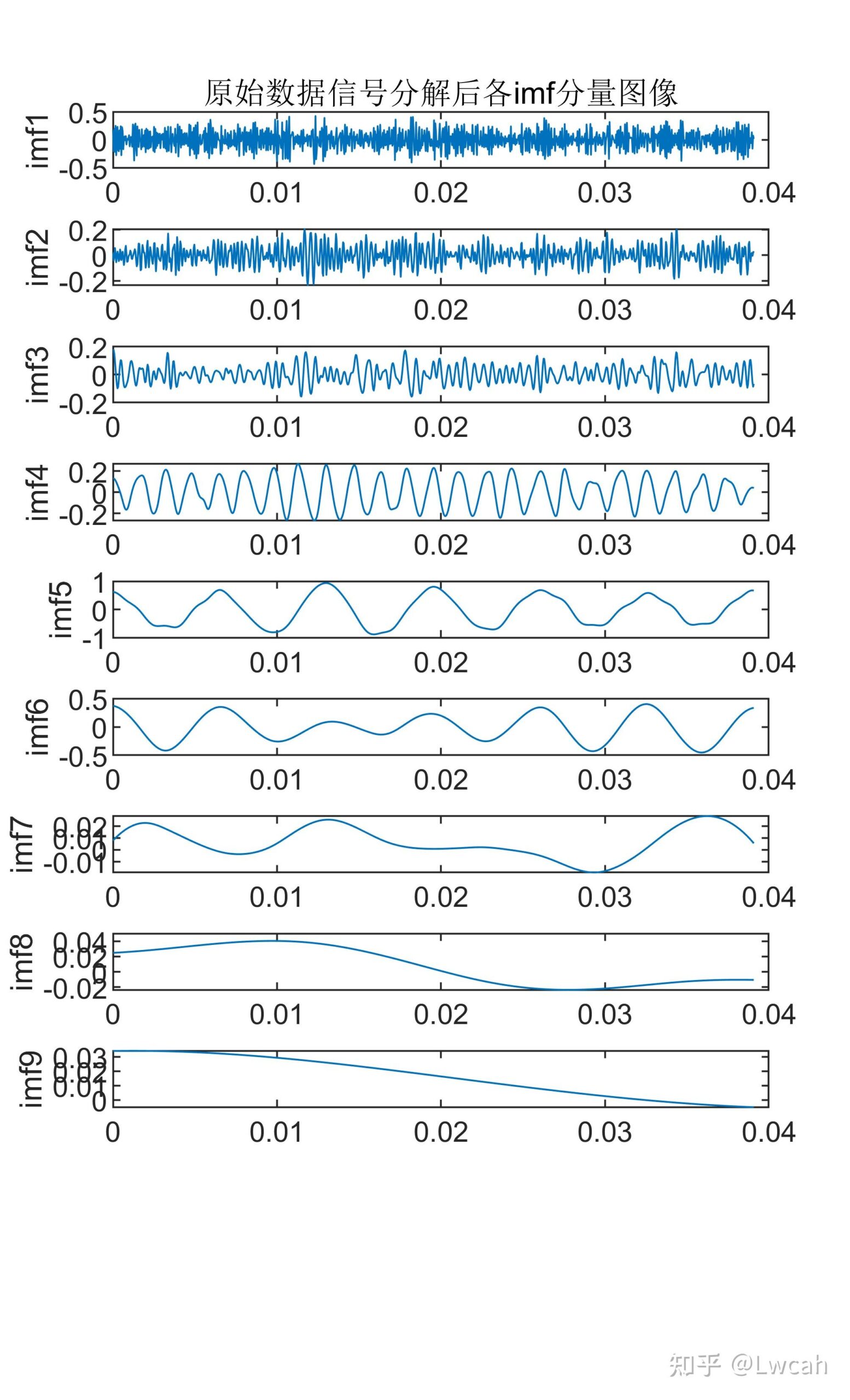
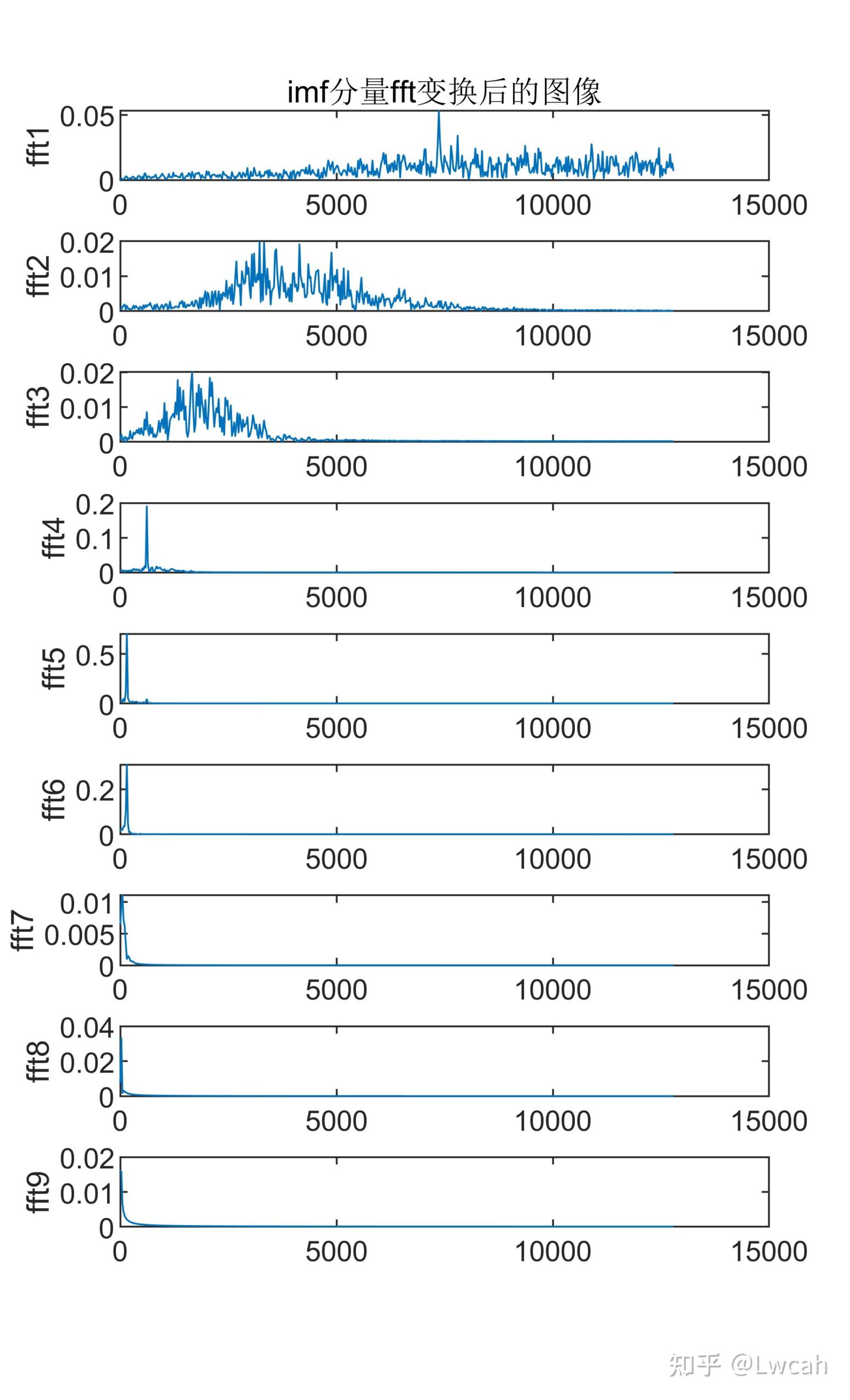
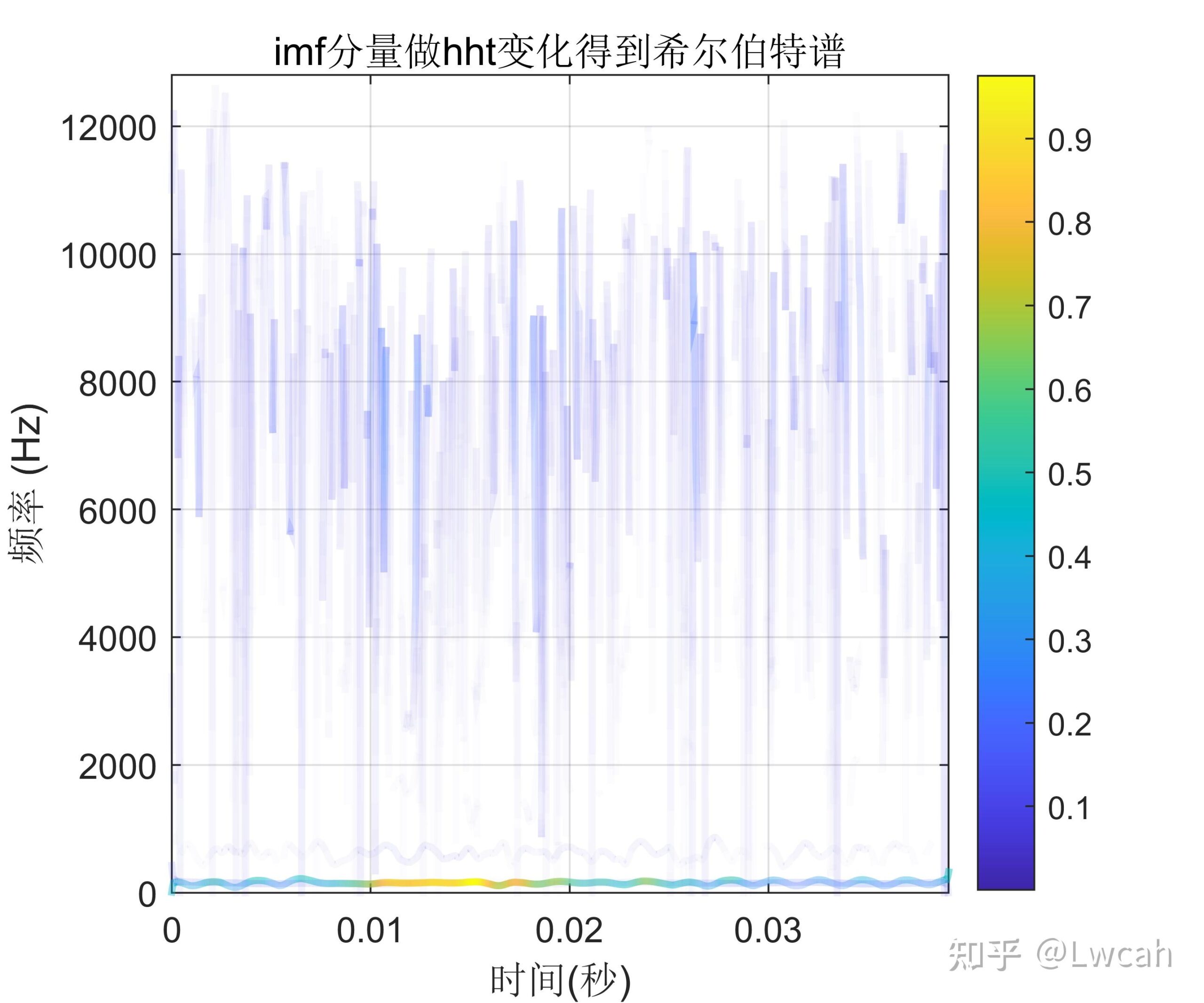
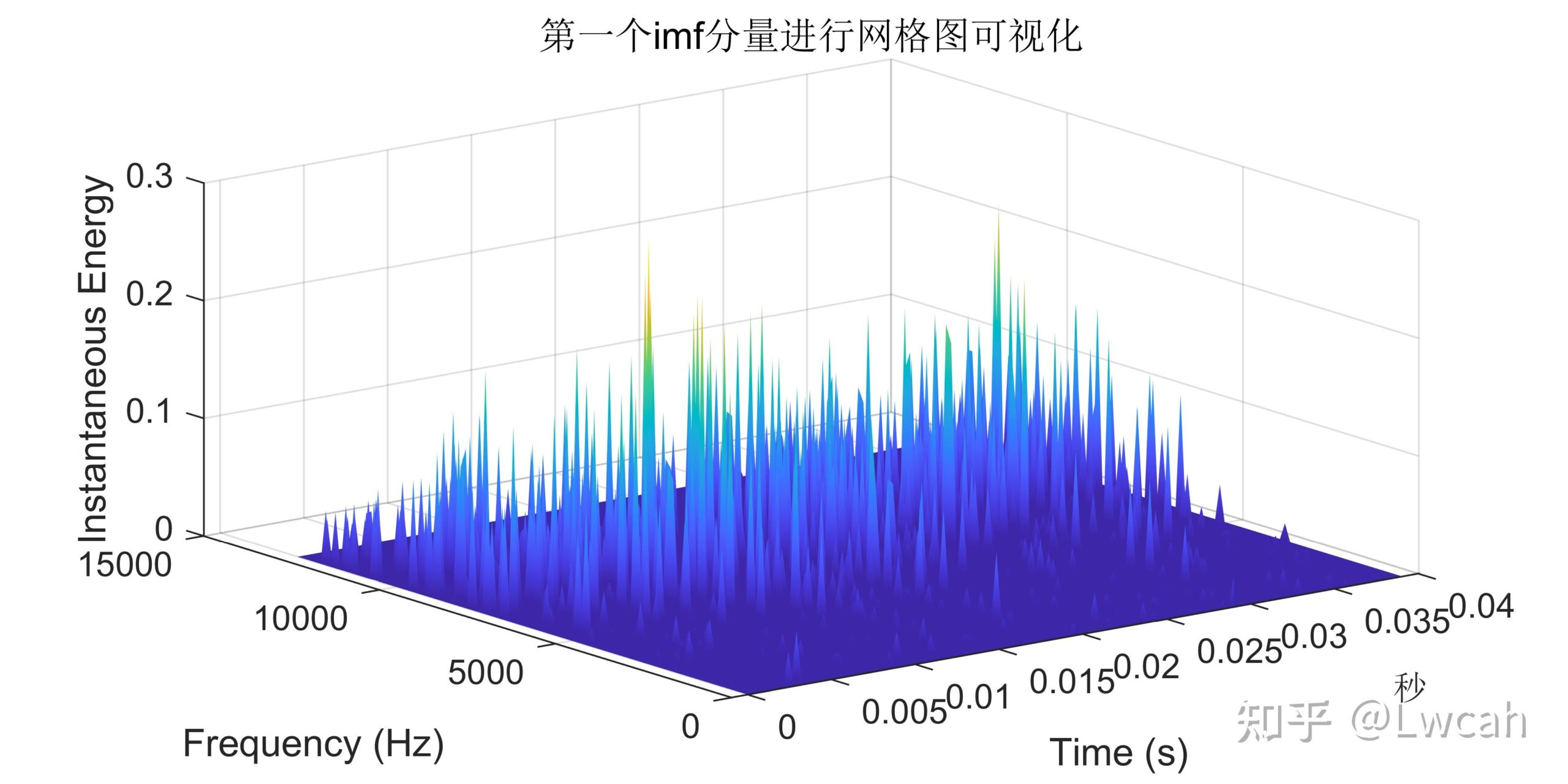
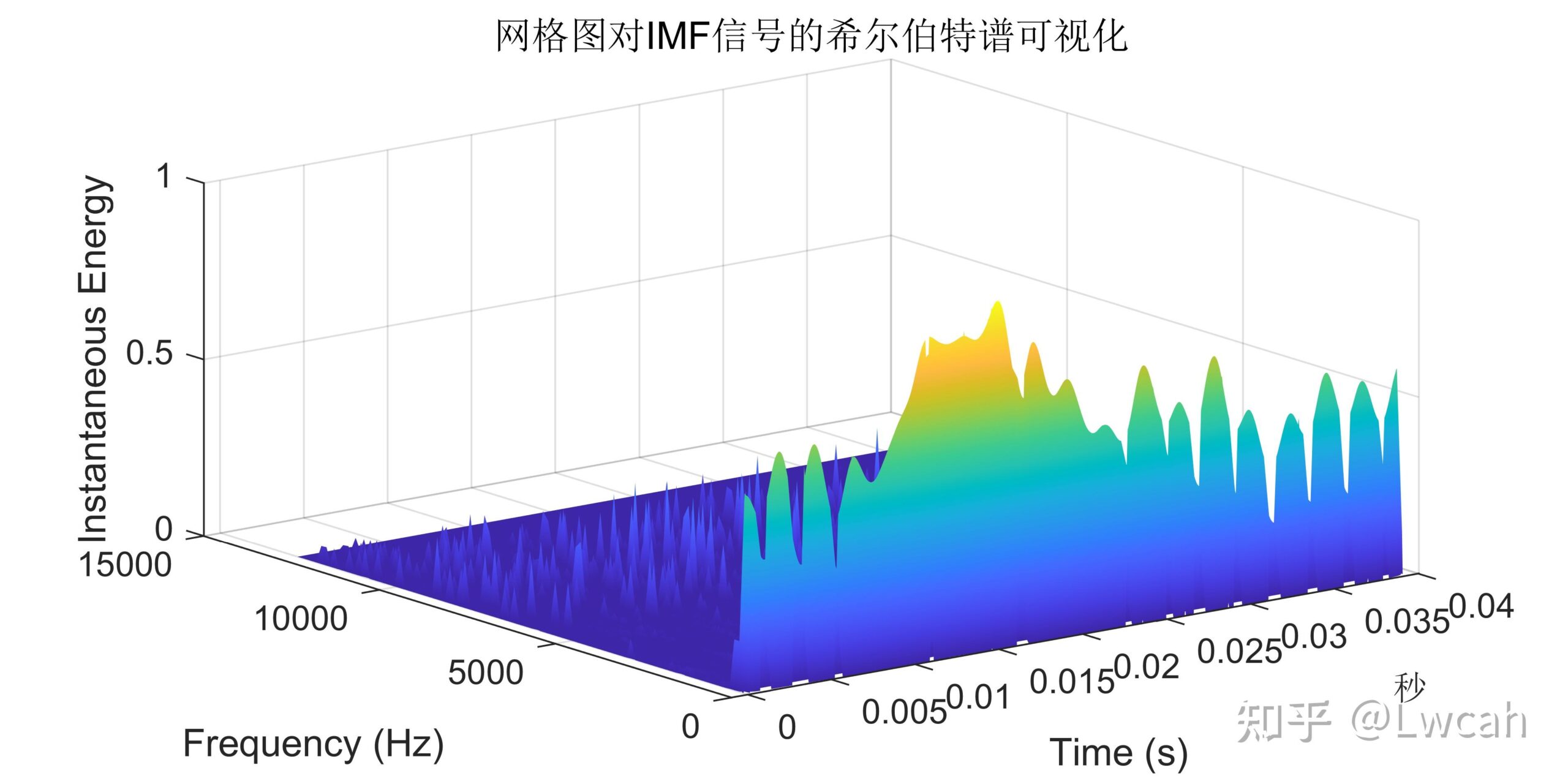
$\Delta f \times 51 = 0.78125 \times 51 = 39.84375Hz$ 　　当N=1024时，还是由于“栅栏效应”，所以幅值也不对。王俊：1周学FFT——第2天 DFT和IDFT的MATLAB实现　　有意向代码，请转文末观看代码方式~也可转原文链接~ 　　1 基本定义　　CEEMD+FFT+HHT组合算法是一种综合性的信号分析方法，它结合了CEEMD（完全经验模态分解）、FFT（快速傅里叶变换）和HHT（希尔伯特-黄变换）三种算法的优点。　　CEEMD是一种经验模态分解方法，可以将一个信号分解成有限个固有模态函数（IMF）的和，每个IMF都是具有局部特征的振动模式。该方法能够处理非线性和非平稳信号，并且不需要预先设定基函数。　　FFT是一种高效计算离散傅里叶变换（DFT）及其逆变换的方法，被广泛应用于信号处理、图像处理等领域。其主要思想是通过合理选择样本点，将离散傅里叶变换和逆变换的计算转化为高效计算矩阵乘法和傅里叶级数。FFT可以快速地计算出信号的频谱。　　HHT是一种新的信号分析方法，能够同时提供信号的时间和频率信息，适用于非线性和非平稳信号的分析。HHT主要由EMD和希尔伯特谱分析两部分组成。在EMD中，每个IMF都代表了信号中的一个频率分量，通过选择合适的模态分量，可以将信号的不同频率成分有效地分离。而希尔伯特谱分析则可以对分离出的频率分量进行时间上的分析，进一步揭示信号的频率和时间分布特征。　　在CEEMD+FFT+HHT组合算法中，首先利用CEEMD对信号进行分解，得到一系列的IMF和一个残余分量。对每个IMF进行FFT计算，得到其频谱信息。然后利用HHT对每个IMF进行希尔伯特谱分析，得到每个IMF的时间和频率信息。通过这种组合算法，可以更全面地分析信号的特征，提取出有用的信息。　　需要注意的是，在实际应用中，CEEMD、FFT和HHT的具体算法可能存在一定的差异和优化，以适应不同的应用场景和数据特点。此外，这种组合算法也需要一定的计算资源和时间成本，需要根据实际情况进行选择和应用。　　除了上述提到的优点，CEEMD+FFT+HHT组合算法还有一些其他的优点。　　首先，该算法可以有效地处理非线性和非平稳信号，能够提取出信号中的复杂特征和模式。这使得它在许多领域中都有广泛的应用，例如机械故障诊断、生物医学信号处理、地震勘探等。　　其次，该算法结合了经验模态分解、傅里叶变换和希尔伯特-黄变换三种基本方法，可以相互补充，提高信号分析的精度和可靠性。例如，CEEMD可以弥补传统经验模态分解方法在处理非线性和非平稳信号时的不足，而FFT和HHT则可以提供更全面的频率和时间信息。　　此外，该算法还具有较好的可解释性和可理解性。经验模态分解和傅里叶变换都是经典的信号处理方法，具有广泛的应用基础和理论支持。希尔伯特-黄变换则提供了时间-频率-能量三位一体的完备表述，使得分析结果更加直观和易于理解。　　最后，该算法还具有较好的鲁棒性和适应性。在处理实际信号时，可能会存在噪声干扰、信号缺失等问题。CEEMD+FFT+HHT组合算法能够适应各种复杂情况，通过对信号的分解和频谱分析，能够提取出有用的特征和模式，提高信号处理的效率和精度。　　需要注意的是，虽然CEEMD+FFT+HHT组合算法具有许多优点，但在实际应用中仍需要根据具体情况选择合适的参数和方法。此外，由于该算法涉及到多个步骤和计算过程，因此需要使用合适的编程语言和工具来实现，以保证计算的准确性和效率。　　2 出图效果　　附出图效果如下：

　　附视频教程操作：【MATLAB】CEEMD+FFT+HHT组合算法_哔哩哔哩_bilibili 　　3 代码　　MATLAB 开源算法及绘图代码合集汇总一览　　https://www.aliyundrive.com/s/9GrH3tvMhKf 　　提取码: f0w7

fft的横坐标_fft输出频谱的横纵坐标

相关推荐