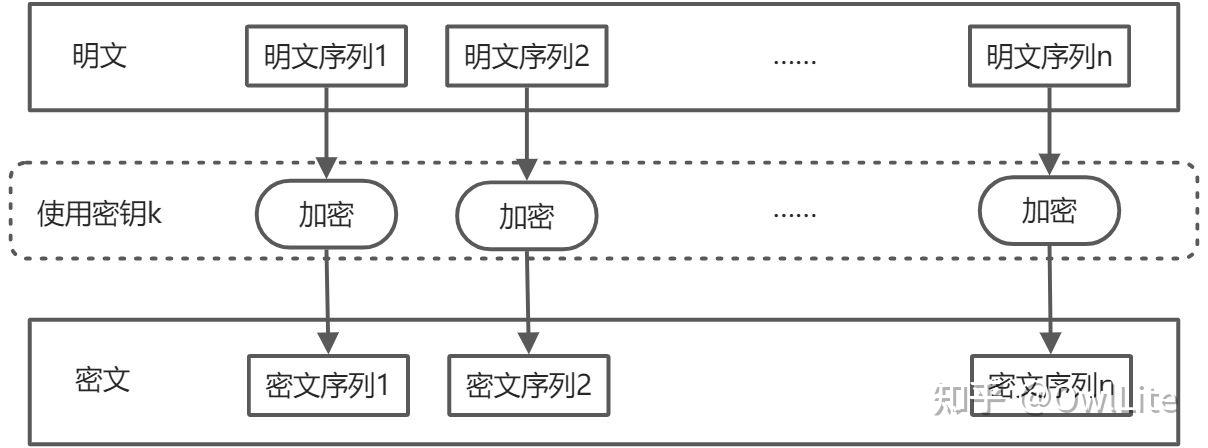
密码学基础体系 密码学本质上是研究加密通信的技术学科，该技术让信息发出者跟指定的信息接受者之间形成可信信道，从而进行第三方不可见的信息传输。从定义上看，密码学跟“加密”就有着紧密的联系，当然，其内涵明显大于后者。 随着 欧洲通用数据保护条例(General Data Protection Regulation, GDPR)和效仿它的《中华人民共和国个人信息保护法》的提出和施行，个人信息保护成为一个越来越重要而且现实的问题。一方面，处理大量用户数据的企业有着合法合规的需要，另一方面，在日渐严格的信息保护规则下，如何发掘这些被加密之后的数据的价值，成为新的迫切应用需求。而密码学 以及强依赖于它的隐私计算技术，自然地成为了一种现实的解决方案。 密码学在计算中的应用，不可避免地会增加通信成本和数据计算成本，相比于明文式的用户数据直接计算，隐私计算目前的计算成本经常要高出数个数量级。这种成本本质上是信任成本，可以划归为经济活动“信息租金”的范畴。 对称密码体制 古典密码学 密码学的最初发展的阶段为古典密码学。在最早的战争时期，同一阵营需要相互传递消息（不管是快马、飞鸽还是电报），为避免重要的情报被敌方，他们会将原本想要传递的消息（被称为明文）利用加密密钥进行加密（密文），从而进行传递。对方收到密文后，会用在战前商量好的解密密钥进行解密，恢复成为明文。 作为古典密码学的最简单形式之一，移位密码非常好理解，举例而言：Alice想要给Bob发送消息“SEEYOUATSCHOOL”，但他们不想让其他人知道消息的内容，那么他们商量好密钥k = 5，将消息中的每个字母按照字典序加五后（模26）的字母表示。即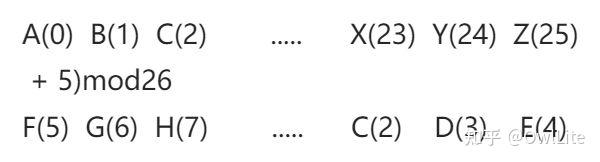
因此，S(18)变为X(23), E(4)变为J(9)…，加密后的密文为 “XJJDTZFYXHMTTQ”Bob收到密文后，将消息中的每个字母按照字典序减五后（模26）的字母表示，则恢复成为了明文，明白Alice约定与他在学校见面。 古典密码还包括了代换密码、放射密码、希尔密码等等，这里就不一一介绍。 分组密码体制 连续的明文用相同的密钥来加密，这样的密码体制为分组密码。详细描述而言，可以认为是将被编码后的明文序列，划分为长度相等的若干组。对于每组使用相同的密钥加密成为等长的密文序列，再按顺序拼接成为完整密文。（上述古典密码学中的密码体制中的移位密码，其实就属于每组序列长度为1的分组密码。）
商密中的分组密码标准[1]为SM4，国际分组密码标准包括AES[2]、3DES[3]、IDEA[4]. 流密码 流密码在加密过程中不会一直使用相同的密钥，而是由密钥种子生成一个密钥流，然后利用加密算法会逐字节的使用密钥流来加密明文流，从而产生密文流。这里的密钥流可以通过硬件（线性反馈移位寄存器）的方式实现。
哈希函数 密码学上的哈希函数可为数据完整性提供保障。哈希函数通常用来构造数据的短“指纹”：一旦数据改变，指纹就不再正确。通常指纹也被称为“消息摘要”。 哈希函数具有的重要特性为单向性，即消息A，哈希之后变为消息摘要B，但是由B却很难推出A。 所以安全的哈希函数需要抗击以下三种攻击：抗原像攻击：B推不出A抗第二原像攻击：无法找到A’，使得A’推出B抗碰撞攻击：多次尝试，无法碰撞出B的消息A。（md5[5]已经被碰撞攻击攻破，目前不再使用） 对称密码体制的缺陷 对称密码体制的加密密钥e和解密密钥d或者相同，或者解密密钥还可以从加密密钥容易的导出。所以它需要消息传递的两方（比如Alice 和 Bob）在首次传输密文之前，使用一个安全信道来协商密钥。实际上在过去这是很难达到的。 非对称密码-公钥密码体制 非对称密码体制，又称为公钥密码体制，显然其与对称密码体制最根本的区别在于加密密钥和解密密钥是非“对称”的：即由加密密钥e推出解密密钥d是计算上不可行的。 因此，非对称密码体制和对称密码体制在用法上就会有所区别：对称密码体制可以用于两方相互沟通，Alice可以传递消息给Bob，Bob也可以使用用同一套密码传递消息给Alice；但非对称密码体制却可以这样使用，Alice把自己的加密密钥（公钥）e公布给允许向她传递消息的Bob、Cathy、David…，而只有Alice自己才拥有解密密钥（私钥）d，这样Bob、Cathy、David都可以用e加密消息传递给Alice，而只有她自己才可以进行解密。 公钥，即可以公布出的钥匙，所以非对称密码体制通常被称为公钥密码体制。因此公钥密码体制并不需要一个预先共享/协商密钥的安全信道。 构建公钥密码体制的核心在于陷门单向函数。 单向函数：一个函数容易计算却难于求逆 陷门单向函数：一个单向函数，在具有特定陷门的知识（私钥）后容易求出其逆 公钥密码算法 现实中，多用公钥密码算法去加密一个对称密码算法的密钥，然后使用对称密码算法来加密一个大的数据（大文件 or 视频）。原因是公钥密码算法的速度比对称密码算法会慢几个数量级。 所以公钥密码体制通常用来做两件事情，1. 加密对称密码的密钥；2. 数字签名。 商密公钥加密标准：SM2信封加密。国际公钥加密标准包括RSA[6]、ECIES[7]、E1Gamal[8]等 数字签名 顾名思义，签名是为了证明消息公布者的身份。所以签名与加密的公私钥相反，加密密钥是私钥，而解密密钥才是公钥。 签名：签名者用私钥作用在明文上，生成签名。将（消息、签名）发布后，所有的验证者可以用公钥进行验证。 验证：验证者用公钥 + 签名计算出一个值，若这个值与提前公布好的值相等，则验证成功。 数字签名可以保证签名和消息的完整性，同时也可以满足抗抵赖性的要求。 商密数字签名标准：SM2数字签名算法。国际数字签名标准包括RSA、ECDSA、DSA等 常用公钥密码体制 RSA密码体制 RSA是人类发现的第一个公钥密码算法，由Ron Rivest、Adi Shamir、Leonard Adleman三人提出，RSA就是他们的姓氏首字母拼接得到的。 RSA的数学基础是大数因子分解困难。具体算法描述如下：Alice任意选取两个不同的大素数p、q，计算二者乘积
，则 选择大整数e，且 ，作为加密密钥（公钥）使用扩展欧几里得求出e对于 的模拟d，即满足 . d就是解密密钥（私钥）。Alice公开整数n和e，秘密保存d。Bob加密： 对于明文m，使用公钥e进行加密 – ， 形成密文c. 将c发送给Alice。Alice解密：对于密文c，使用私钥d进行解密 – ，计算出Bob的明文m. 消息传递成功 . 这里的 ，是由数论中的拉格朗日定理推理得到的。这里解释大数因子分解困难为什么是RSA的数学基础：在4中，Alice公布了整数n和e，如果对n可以轻易的计算出因子分解后的p和q，那么就可以直接计算出 ，那么任何人在知道 的情况下都可以计算出私钥d，那么他就可以对所有的密文进行解密，这套密码也就被完全攻破了。为何大数因子分解是困难的呢？对于一个大数n，想要对它最分解只有暴力搜索所有可能的解这一种方式，对于一个足够大的数，解它的时间复杂度是O(n)。当然，我们的“足够大”是相对于计算资源而言的，对于普通cpu和量子计算机的“足够大”的n肯定不是同一量级。 RSA的签名算法 消息签名者Alice任意选取两个不同的大素数p、q，计算二者乘积 ，则 选择大整数e，且 ，作为加密密钥（私钥）使用扩展欧几里得求出e对于 的模拟d，即满足 . d就是解密密钥（公钥）。Alice公开整数n和d，秘密保存e。Alice签名：对于消息x， ，公布（x，y）Bob验证：若计算 得到的结果与x相等，则验证成功，证明消息是Alice发布的，否则验证失败。 第一种量子计算算法秀尔算法，把分解整数质因素的指数时间复杂度 缩减到多项式时间 [9]，这意味着，依赖大数因数分解困难性的RSA加密算法，在量子计算下变得不再安全了[10]. E1Gamal密码体制 E1Gamal密码体制是基于求解离散对数困难的问题，这里介绍最基础的E1Gamal密码体制，基于椭圆曲线的E1Gamal密码体制（ECC）这里就不展开描述了。具体算法如下：Alice取一个大素数p, 是 的一个本原。 的阶为 ，即 .Alice公布 ，a为私钥Bob加密：秘密选取随机数 ， 对明文m加密后的结果为 , 将 发送给Alice. 其中 Alice解密： . 其中 这里解释求解离散对数困难为什么是E1Gamal的数学基础：由于 都已经被公布出来，如果求解离散对数并不困难，那么私钥 便可被任何人求出。显然，这样的密码体制是不安全的。为何求解离散对数困难是困难的呢？求解对数是计算 ，这本身并不困难（可用泰勒展开），但要在模p的正整数中寻找 结果，是非常困难的。
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/55352.html
