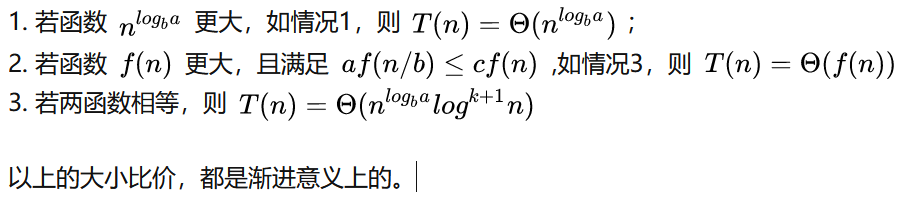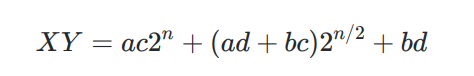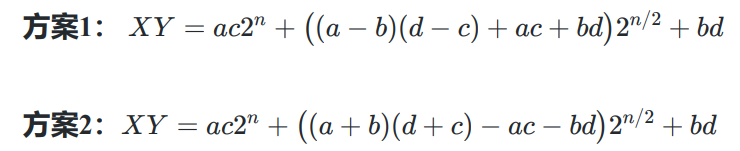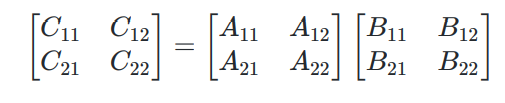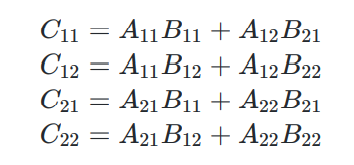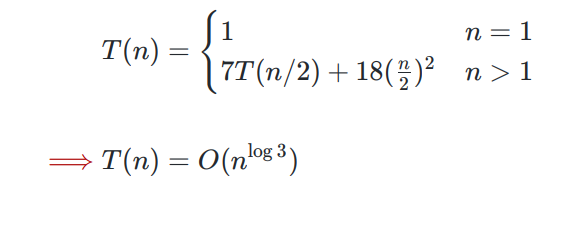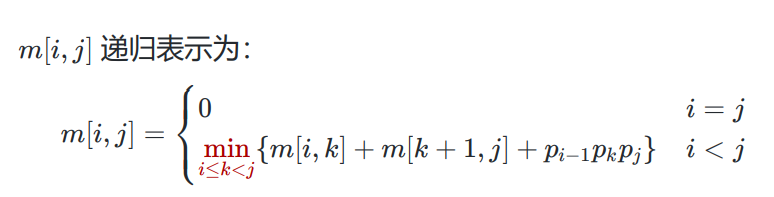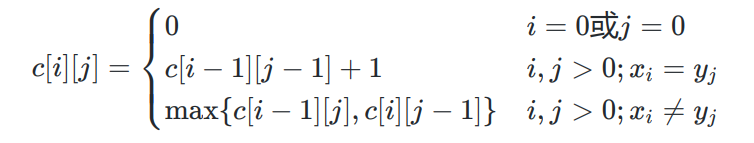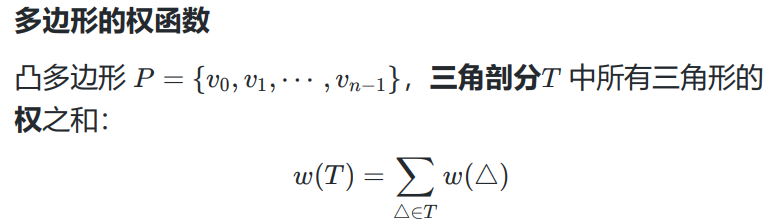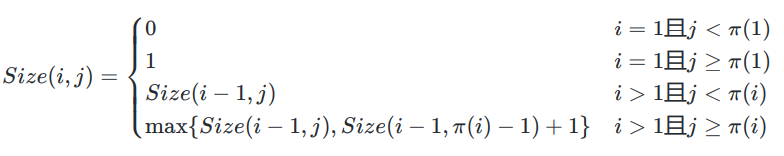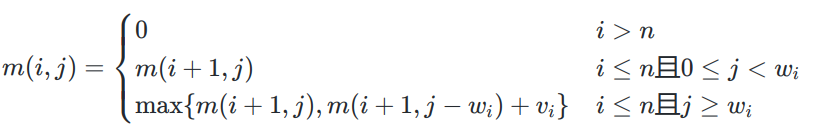哈夫曼树的算法实现_哈夫曼树算法思想2021BNU算法期末复习提纲复杂度分析master主定理计算时间复杂度排序归并排序1)分:将序列分成两个子序列,分别进行排序,递归求解2)治:将排序好的子序列不断比较生成一个顺序的序列时间复杂度空间复杂度快速排序坑填数+分治法平均时
2021BNU算法期末复习提纲 复杂度分析 master主定理计算时间复杂度





 排序 归并排序 1)分:将序列分成两个子序列,分别进行排序,递归求解 2)治:将排序好的子序列不断比较生成一个顺序的序列
排序 归并排序 1)分:将序列分成两个子序列,分别进行排序,递归求解 2)治:将排序好的子序列不断比较生成一个顺序的序列

 时间复杂度 空间复杂度 快速排序
时间复杂度 空间复杂度 快速排序

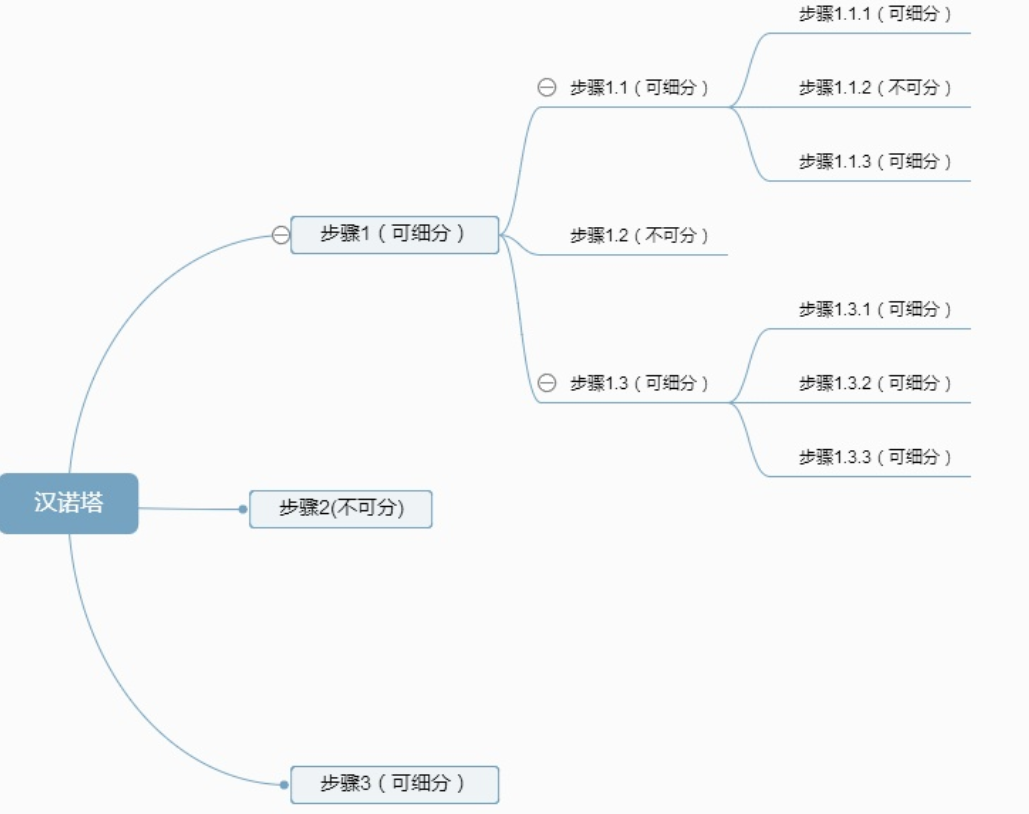
 坑填数+分治法 平均时间复杂度 最坏时间复杂度 空间复杂度 递归 汉诺塔问题 将n个环从小到大标为1,2,3…n 三根柱子(从左到右标为a,b,c): 1.只有两个环的情况 1)将1移到c上,交换b和c,此时c在中间位置 a,c,b 2)将2移到b上,交换a和c,此时c在最左边,b在最右边 c,a,b 3)将1移到b上。 c,a,b 即第一步是将1通过c移到b上,然后移动2(最大环)到c,然后将1通过a移动到c上 2.有n个环的情况 1)将前n-1个视为整体 2)不断递归求得最终解
坑填数+分治法 平均时间复杂度 最坏时间复杂度 空间复杂度 递归 汉诺塔问题 将n个环从小到大标为1,2,3…n 三根柱子(从左到右标为a,b,c): 1.只有两个环的情况 1)将1移到c上,交换b和c,此时c在中间位置 a,c,b 2)将2移到b上,交换a和c,此时c在最左边,b在最右边 c,a,b 3)将1移到b上。 c,a,b 即第一步是将1通过c移到b上,然后移动2(最大环)到c,然后将1通过a移动到c上 2.有n个环的情况 1)将前n-1个视为整体 2)不断递归求得最终解

 四根柱子(从左到右标为a,b,c,d): n个环:
四根柱子(从左到右标为a,b,c,d): n个环:

 分治 大整数乘法 n位整数和m位整数相乘,将n位分成a,b两段,m位分成c,d两段;n=a+b,m=c+d; 将两个大整数拆分成如下的形式
分治 大整数乘法 n位整数和m位整数相乘,将n位分成a,b两段,m位分成c,d两段;n=a+b,m=c+d; 将两个大整数拆分成如下的形式

 尽量减少乘法的次数,甚至可以用因式分解和配凑,来减小时间复杂度
尽量减少乘法的次数,甚至可以用因式分解和配凑,来减小时间复杂度

 矩阵乘法
矩阵乘法

 for循环 时间复杂度 分治法1 :n阶矩阵分块乘法
for循环 时间复杂度 分治法1 :n阶矩阵分块乘法



 n * n —> n/2 * n/2 8次乘法 + 4次加法 时间复杂度还是 分治法2 : 矩阵乘法
n * n —> n/2 * n/2 8次乘法 + 4次加法 时间复杂度还是 分治法2 : 矩阵乘法



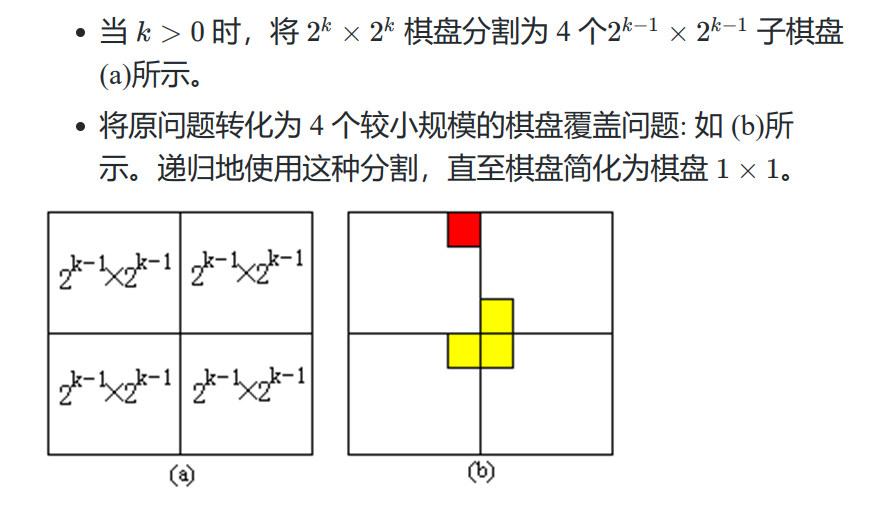
 棋盘覆盖
棋盘覆盖

 分割,在四个子棋盘中生成一个L型框,递归,覆盖 动态规划 分治法要求子问题相互独立,当子问题发生重叠时,子问题被重复计算,浪费计算资源。 动态规划在求解子问题时将每个子问题计算后保存答案,避免重复计算。 动态规划时常用于全局寻优,将待求解问题分解成若干个子问题,满足一定条件时原问题的最优解可以通过子问题的最优解计算得出。 动态规划需要证明解具有最优子结构性质(一般用反证法)。 动态规划算法的两大要素 1)最优子结构特性;2)重叠子问题特性。 矩阵连乘积 矩阵A,B,C,D求乘积 1.穷举法暴力计算
分割,在四个子棋盘中生成一个L型框,递归,覆盖 动态规划 分治法要求子问题相互独立,当子问题发生重叠时,子问题被重复计算,浪费计算资源。 动态规划在求解子问题时将每个子问题计算后保存答案,避免重复计算。 动态规划时常用于全局寻优,将待求解问题分解成若干个子问题,满足一定条件时原问题的最优解可以通过子问题的最优解计算得出。 动态规划需要证明解具有最优子结构性质(一般用反证法)。 动态规划算法的两大要素 1)最优子结构特性;2)重叠子问题特性。 矩阵连乘积 矩阵A,B,C,D求乘积 1.穷举法暴力计算

 2.动态规划求解 最优解的结构特征(最优子结构性质/最优性原理):的最优计算次序 —> 和 计算次序最优
2.动态规划求解 最优解的结构特征(最优子结构性质/最优性原理):的最优计算次序 —> 和 计算次序最优



 子问题:即(i,j)对的取值个数 非递归法: public static void matrixChain(int [] p, int [][] m, int [][] s){ int n=p.length-1; for (int i = 1; i <= n; i++) m[i][i] = 0; for (int r = 2; r <= n; r++) for (int i = 1; i <= n – r+1; i++) { int j=i+r-1; m[i][j] = m[i+1][j]+ p[i-1]*p[i]*p[j]; s[i][j] = i; for (int k = i+1; k < j; k++) { int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j]; if (t < m[i][j]) { m[i][j] = t; s[i][j] = k; } } }} 递归算法: int RecurMatrixChain(int i, int j){ if (i==j) return 0; int u=RecurMatrixChain(i, i) + RecurMatrixChain(i+1, j) +p[i-1]*p[i]*p[j]; s[i][j]=i; for (int k = i+1; k < j; k++) { int t =RecurMatrixChain(i, k) + RecurMatrixChain(k+1, j)+p[i-1]*p[k]*p[j]; if (t < u) { u = t; s[i][j] = k; } } return u;} 最长公共子序列
子问题:即(i,j)对的取值个数 非递归法: public static void matrixChain(int [] p, int [][] m, int [][] s){ int n=p.length-1; for (int i = 1; i <= n; i++) m[i][i] = 0; for (int r = 2; r <= n; r++) for (int i = 1; i <= n – r+1; i++) { int j=i+r-1; m[i][j] = m[i+1][j]+ p[i-1]*p[i]*p[j]; s[i][j] = i; for (int k = i+1; k < j; k++) { int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j]; if (t < m[i][j]) { m[i][j] = t; s[i][j] = k; } } }} 递归算法: int RecurMatrixChain(int i, int j){ if (i==j) return 0; int u=RecurMatrixChain(i, i) + RecurMatrixChain(i+1, j) +p[i-1]*p[i]*p[j]; s[i][j]=i; for (int k = i+1; k < j; k++) { int t =RecurMatrixChain(i, k) + RecurMatrixChain(k+1, j)+p[i-1]*p[k]*p[j]; if (t < u) { u = t; s[i][j] = k; } } return u;} 最长公共子序列

 case 1: 有一个序列为空
case 1: 有一个序列为空

 case 2: 序列最后一个素相等
case 2: 序列最后一个素相等

 case 3: 序列最后一个素不相等
case 3: 序列最后一个素不相等

 综上所述可以建立递归关系:
综上所述可以建立递归关系:

 动态规划算法:
动态规划算法:

 计算序列长度:
计算序列长度:

 凸多边形最优三角剖分 任意三角剖分T中, 1)各弦不相交,且集合T达到最大(即不在集合T中的弦至少和T中的一条弦相交); 2)恰有n-3条弦和n-2个三角形 权的概念: 1)
凸多边形最优三角剖分 任意三角剖分T中, 1)各弦不相交,且集合T达到最大(即不在集合T中的弦至少和T中的一条弦相交); 2)恰有n-3条弦和n-2个三角形 权的概念: 1)

 2)
2)

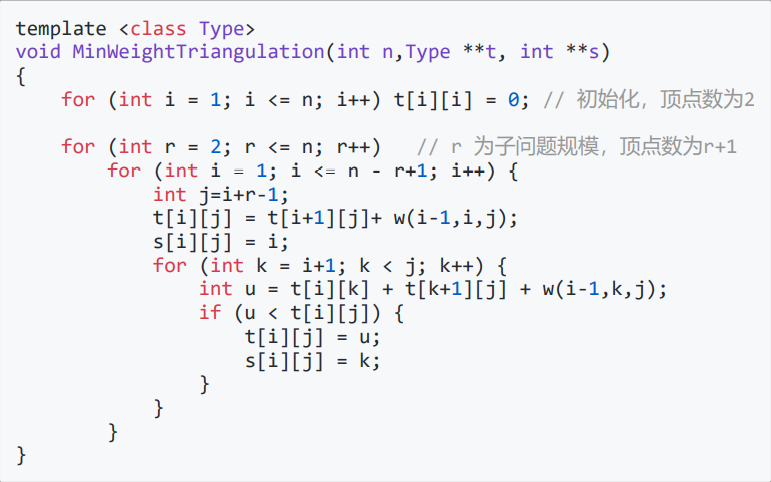
 权最小的剖分就是最优三角剖分 凸n+1边形的最优三角剖分可以分为两个子多边形的最优三角剖分和一个三角形 算法:
权最小的剖分就是最优三角剖分 凸n+1边形的最优三角剖分可以分为两个子多边形的最优三角剖分和一个三角形 算法:

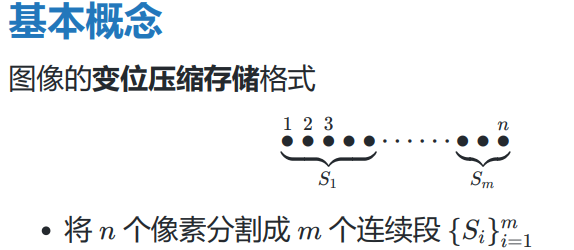
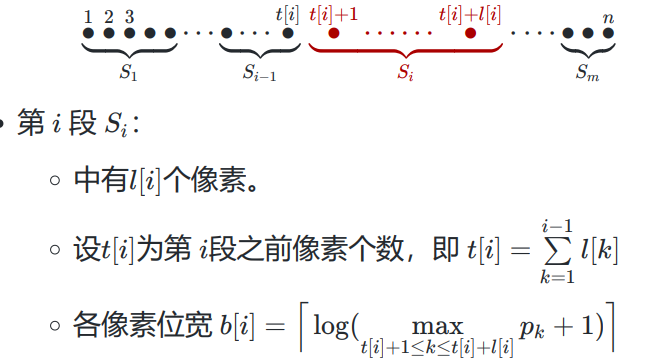
 图像压缩
图像压缩



 最优子结构性质: 假设最优分段,表示出子问题的最优分段,用反证法求解。 递归公式:
最优子结构性质: 假设最优分段,表示出子问题的最优分段,用反证法求解。 递归公式:

 电路布线 给定的上下接线柱的映射关系 ,确定导线集的最大不相交子集 连线和条连线相交的充要条件为
电路布线 给定的上下接线柱的映射关系 ,确定导线集的最大不相交子集 连线和条连线相交的充要条件为

 最优子结构性质:
最优子结构性质:



 其他思路:
其他思路:

 流水作业调度(!!!)
流水作业调度(!!!)





 0-1背包问题 最优子结构:
0-1背包问题 最优子结构:

 剩余重量:
剩余重量:

 递归关系:
递归关系:

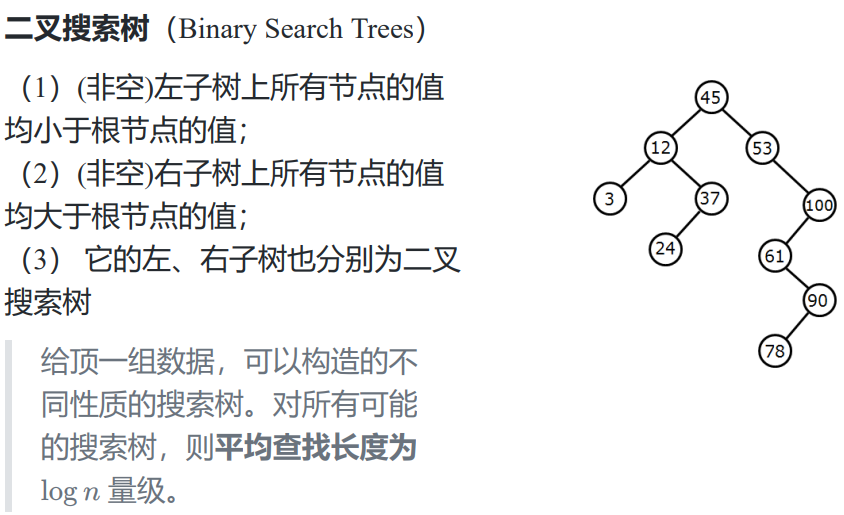
 最优二叉搜索树 基本概念:
最优二叉搜索树 基本概念:

 最优检索树问题: 在所有可能的建树的方案 中选择期望耗费 最少的树 最优子结构性质:
最优检索树问题: 在所有可能的建树的方案 中选择期望耗费 最少的树 最优子结构性质:

 通过计算查找到各个节点的概率和期望值,来证明最优子结构性质
通过计算查找到各个节点的概率和期望值,来证明最优子结构性质

 贪心算法 活动安排问题
贪心算法 活动安排问题

 贪心算法的基本要素 1)贪心选择性质:问题的整体最优解可以通过一系列局部最优策略(即贪心选择)得到;通常采用自顶向下的形式,每做一次贪心选择之后,问题化简为更小规模的子问题; 2)最优子结构性质 分数背包问题 贪心算法求解,基本步骤: 1)计算每种物品单位重量的价值 2)贪心策略将单位重量价值最高的物品尽量装入背包,若未超过背包容量,则继续…直到背包装满。 涉及到对单位重量价值的排序 最优装载 在不超过总载重的情况下,将尽可能多个数的物品装到容器里边,第个物品的重量为.(物品的体积不受限制) 贪心选择属性: 每次从集装箱中选择重量最小的,直到总载重量不超过容量限制的最大值
贪心算法的基本要素 1)贪心选择性质:问题的整体最优解可以通过一系列局部最优策略(即贪心选择)得到;通常采用自顶向下的形式,每做一次贪心选择之后,问题化简为更小规模的子问题; 2)最优子结构性质 分数背包问题 贪心算法求解,基本步骤: 1)计算每种物品单位重量的价值 2)贪心策略将单位重量价值最高的物品尽量装入背包,若未超过背包容量,则继续…直到背包装满。 涉及到对单位重量价值的排序 最优装载 在不超过总载重的情况下,将尽可能多个数的物品装到容器里边,第个物品的重量为.(物品的体积不受限制) 贪心选择属性: 每次从集装箱中选择重量最小的,直到总载重量不超过容量限制的最大值



 哈夫曼编码 根据字符出现的频率,用0,1串表示各字符的最优表示方式—-基本思路:高–短,低–长 自底向上构造表示最优前缀码的二叉树。(构造哈夫曼树) 单源最短路径 计算带权有向图内一个源点到其他各点的最短路径长度(Dijkstra算法) 最小生成树 各边的权的总和最小的生成树叫做最小生成树 算法
哈夫曼编码 根据字符出现的频率,用0,1串表示各字符的最优表示方式—-基本思路:高–短,低–长 自底向上构造表示最优前缀码的二叉树。(构造哈夫曼树) 单源最短路径 计算带权有向图内一个源点到其他各点的最短路径长度(Dijkstra算法) 最小生成树 各边的权的总和最小的生成树叫做最小生成树 算法



 算法
算法

 多机调度问题 回溯法 回溯法的算法框架
多机调度问题 回溯法 回溯法的算法框架

 完备性特点:若E中前j项不满足约束集,则不是有效解
完备性特点:若E中前j项不满足约束集,则不是有效解

 一般的深度搜索
一般的深度搜索

 带剪枝的深度优先搜索——回溯法(添加一个剪枝的约束条件)
带剪枝的深度优先搜索——回溯法(添加一个剪枝的约束条件)

 两种解空间结构 1)子集树(用边来表示是否选中,左分支记为1,右分支记为0);2)排列树(第i层边表示排列中的第i个素) 装载问题(子集树)
两种解空间结构 1)子集树(用边来表示是否选中,左分支记为1,右分支记为0);2)排列树(第i层边表示排列中的第i个素) 装载问题(子集树)

 1.将第一艘轮船尽可能装满(0-1背包问题) 2.将剩余集装箱装上第二艘轮船 可行性约束:
1.将第一艘轮船尽可能装满(0-1背包问题) 2.将剩余集装箱装上第二艘轮船 可行性约束:

 取值为0或1 限界函数:
取值为0或1 限界函数:

 批处理作业调度(排列树) n个作业先后由机器1,2处理 ??? 符号三角形问题
批处理作业调度(排列树) n个作业先后由机器1,2处理 ??? 符号三角形问题

 第一行有n个符号,计算可以有多少个不同的符号三角形 算法思路:n-1个符号确定了子符号三角形,增加第n个符号则符号三角形右侧增加一条边 回溯法:子集树(符号三角形第一行的符号取值) 可行性约束函数:符号三角形所包含的+和-的个数均不超过 无解:若总符号数为奇数,则+和-的个数不相等,即无解 n皇后问题 任意两个皇后不能放在同一行、同一列或同一斜线上
第一行有n个符号,计算可以有多少个不同的符号三角形 算法思路:n-1个符号确定了子符号三角形,增加第n个符号则符号三角形右侧增加一条边 回溯法:子集树(符号三角形第一行的符号取值) 可行性约束函数:符号三角形所包含的+和-的个数均不超过 无解:若总符号数为奇数,则+和-的个数不相等,即无解 n皇后问题 任意两个皇后不能放在同一行、同一列或同一斜线上

 0-1背包问题
0-1背包问题

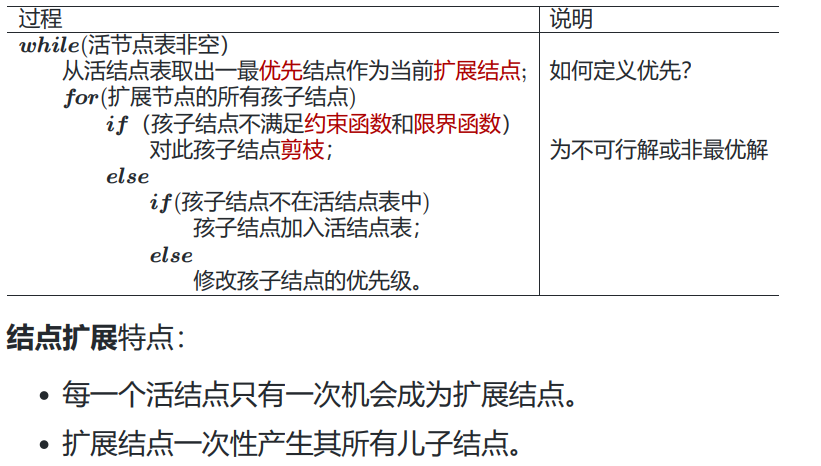
 分支限界法 基本思想
分支限界法 基本思想


2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。
文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/52016.html