[数据结构笔记]8 二叉搜索树及其常见操作 1、查找问题：分静态查找和动态查找 [静态查找] 如果是有序序列，二分查找比顺序查找快很多。 查找次数==发生比较的次数，取决于生成二叉判定树的深度 由于二叉判定树是完全二叉树，所以判定树深度是：[log2 n]+1 换算阶O（log2 n） 最好：1 最坏：O（log2 n） [动态查找] 查找序列可能有增删素，不过始终保证是有序排列 -》 这种问题借助 二叉搜索树（普通的树没有排序，就没法确定新增素的位置了，所以一定是搜索树）。 二叉搜索树可能是完全二叉树，也可能不是。 依然，查找次数==发生比较的次数，因此最坏情况下的搜索效率依然取决于树深度。 同一n个节点按照搜索树规则建立搜索树，形成的树并不确定。只有顺序确定树才是唯一的。 同一n个节点，根据插入顺序不同，会形成不同深度的二叉搜索树，不过都满足左树所有<根<右树所有的规则：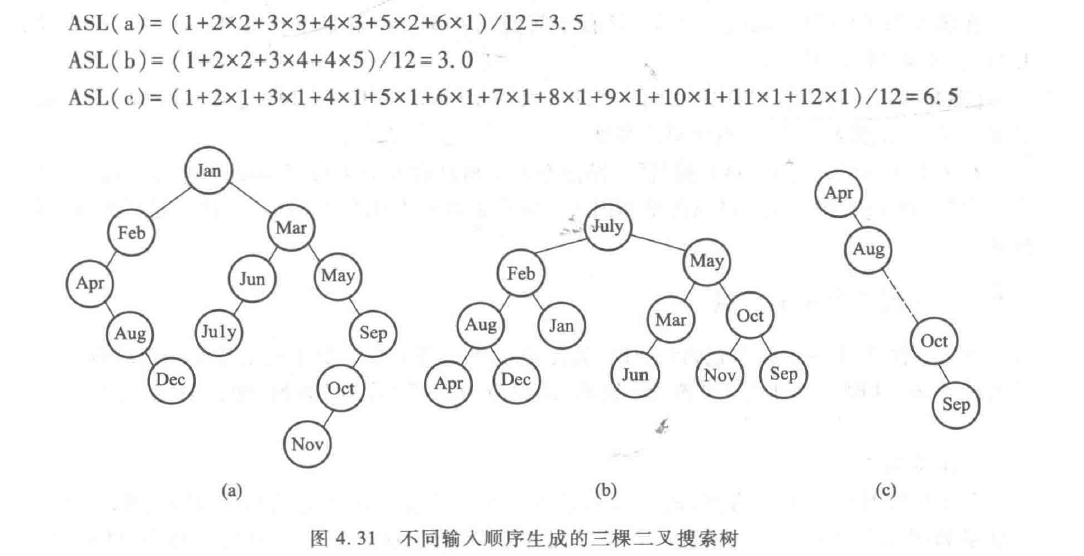
ASL是平均计算长度，都叫搜索树……它们的查找效率不同 越接近完全二叉树，深度越小，ASL也越小，效率整体越高： 如果n个节点排成完全二叉树，搜索次数最大值O（log n），这是最理想的； 如果n个节点排成斜二叉树，搜索次数最大值O（ n），这是最不理性的； 这说明安排插入的顺序很关键，毕竟建树就是为了查找！ 尽量建成完全二叉树，实在不行就尽量建成接近它的平衡树 如果不是完全二叉树，但是接近完全二叉树，也能获得不错的效率，搜索次数最大值接近O（log n），仅次于完全二叉树， -》后面的平衡二叉树 2、二叉搜索树 BST 左树所有<根<右树所有 常见的操作：findXfindMinfindMaxinsertXdeleteX 3、findX的实现 1）递归实现 这是一个尾递归，尾递归都可以用循环实现。 2）迭代实现 效率与树的高度有关。 而同样n个节点的树，高度是不同的。尽量平衡高度会比较小。 4、findMin的实现(可递归可迭代）找到最靠左的素） 5、findMax同理，这里用迭代 化简 6、insertX 这个插入不需要改变已有！只是新增一个叶子节点 用了递归 关于为什么函数有返回？为了递归的实现！ 递归到尽头时，不仅要新建一个节点，还要让已经存在的上一个节点指向它。不返回去递归调用的上一层，如何做到？ 7、deleteX 删除一个节点需要考虑父节点和子节点。 可能会改变父节点的Next； 删除的节点可能有0、1、2个子节点，分别考虑。子节点如果存在，需要用字节点填充。 尤其是有2个子节点的情况，应取左子树最大，或者，右子树最小。 找到待删除素bt时，怎么样再去找到父节点（需要修改Next）？ 这里依然用递归返回，把bt返回到上一层递归函数，那里就有父节点。 这里函数返回仅2种可能：删了没有填充返回NULL，删了被填充或者没有找到返回原bt 因此这样bt->right=deleteX(bt->right,X);没有问题。 8、判断题 若一搜索树（查找树）是一个有n个结点的完全二叉树，则该树的最大值一定在叶结点上.（x） 完全二叉树的最大值可能有左儿子，所以最大值不一定在叶结点上 若一搜索树（查找树）是一个有n个结点的完全二叉树，则该树的最小值一定在叶结点上.（√） 感觉最小值节点也可能有右儿子?只有有右儿子一定有左儿子，才是完全二叉树！
2024最新激活全家桶教程，稳定运行到2099年，请移步至置顶文章：https://sigusoft.com/99576.html
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请联系我们举报，一经查实，本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处：https://sigusoft.com/46936.html
