三种时间复杂度算法求解斐波那契数列 0. 问题描述 在数学当中,由斐波那契数字(Fibonacci number,记作




















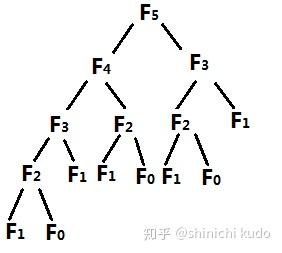



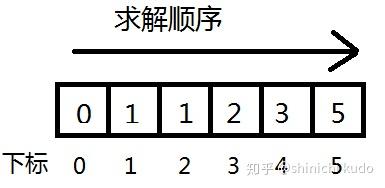






![二叉树的时间复杂度和空间复杂度_二叉树前中后序遍历插图39 \left[\begin{array}{cccc} F_2 \\ F_1 \\ \end{array}\right] = \left[\begin{array}{cccc} 1 & 1 \\ 1 & 0 \\ \end{array}\right] \times \left[\begin{array}{cccc} F_1 \\ F_0 \\ \end{array}\right]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![二叉树的时间复杂度和空间复杂度_二叉树前中后序遍历插图41 \left[\begin{array}{cccc} F_3 \\ F_2 \\ \end{array}\right] = \left[\begin{array}{cccc} 1 & 1 \\ 1 & 0 \\ \end{array}\right] \times \left[\begin{array}{cccc} F_2 \\ F_1 \\ \end{array}\right] = \left[\begin{array}{cccc} 1 & 1 \\ 1 & 0 \\ \end{array}\right]^2 \times \left[\begin{array}{cccc} F_1 \\ F_0 \\ \end{array}\right]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)
![二叉树的时间复杂度和空间复杂度_二叉树前中后序遍历插图43 \left[\begin{array}{cccc} F_n \\ F_{n-1} \\ \end{array}\right] = \left[\begin{array}{cccc} 1 & 1 \\ 1 & 0 \\ \end{array}\right]^{n-1} \times \left[\begin{array}{cccc} F_1 \\ F_0 \\ \end{array}\right] = \left[\begin{array}{cccc} 1 & 1 \\ 1 & 0 \\ \end{array}\right]^{n-1} \times \left[\begin{array}{cccc} 1 \\ 0 \\ \end{array}\right]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)

![二叉树的时间复杂度和空间复杂度_二叉树前中后序遍历插图45 \left[\begin{array}{cccc} F_n \\ F_{n-1} \\ \end{array}\right]](https://sigusoft.com/wp-content/themes/justnews/themer/assets/images/lazy.png)















2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。 文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/42325.html