二叉查找树最好情况下复杂度_二叉树的时间复杂度希赛2022年软件设计师考前N页纸软件设计师考前N页纸数组与矩阵:2、顺序表与链表对比:3、循环链表:队空条件:head=tail;队满条件:(tail+1)%size=head。4、树的概念:(1)双亲、孩
希赛2022年软件设计师考前N页纸 软件设计师考前N页纸 数组与矩阵:

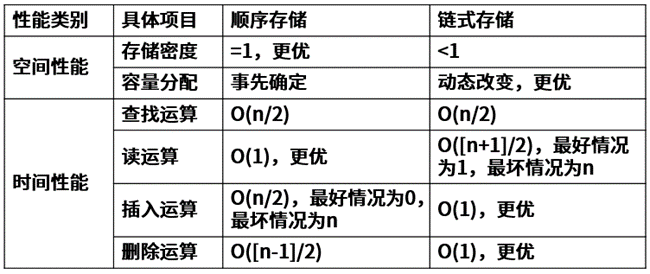
 2、顺序表与链表对比:
2、顺序表与链表对比:

 3、循环链表:队空条件:head=tail;队满条件:(tail+1)%size=head。 4、树的概念: (1)双亲、孩子和兄弟:结点的子树的根称为该结点的孩子;相应地,该结点称为其子结点的双亲。具有相同双亲的结点互为兄弟。 (这里涉及到2个层次,第一个层次的子树,这棵子树的根是第一层结点的孩子结点,第一层结点是其子节点的双亲节点/父节点)。 (2)结点的度:一个结点的子树的个数记为该结点的度 (3)叶子节点:也称为终端结点,指度为0的结点 (4)内部结点:指度不为0的结点,也称为分支节点或非终端节点。除根结点之外,分支结点也称为内部结点。 (5)结点的层次:根为第一层,根的孩子为第二层,依次类推,若某节点在第i层,则其孩子结点在第i+1层 (6)树的高度:一颗树的最大层次数记为树的高度(深度) 5、二叉树的重要特性: (1)在二叉树的第i层上最多有2i-1个结点(i≥1); (2)深度为k的二叉树最多有2k -1个结点(k≥1); (3)对任何一棵二叉树,如果其叶子结点数为n0,度为2的结点数为n2,则n0=n2+1。 (4)如果对一棵有n个结点的完全二叉树的结点按层序编号(从第1层到 L log2n ˩+1层,每层从左到右),则对任一结点i(1≤i≤n),有: 如果i=1,则结点i无父结点,是二叉树的根;如果i>1,则父结点是L i/2 ˩ ; 如果2i>n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i; 如果2i+1>n,则结点i无右子叶点,否则,其右子结点是结点2i+1。 6、特殊的树: (1)二叉树:二叉树是每个结点最多有两个孩子的有序数,可以为空树,可以只有一个结点。 (2)满二叉树:任何结点,或者是树叶,或者恰有两棵非空子树。 (3)完全二叉树:最多只有最小面的两层结点的度可以小于2,并且最下面一层的结点全都集中在该层左侧的若干位置。 (4)平衡二叉树:树中任一结点的左右子树高度之差不超过1。 (5)查找二叉树:又称之为排序二叉树。任一结点的权值,大于其左孩子结点,小于其右孩子结点。 (6)线索二叉树:在每个结点中增加两个指针域来存放遍历时得到的前驱和后继信息。 (7)最优二叉树:又称为哈弗曼树,它是一类带权路径长度最短的树。 7、最优二叉树(哈弗曼树)的构造过程:(1)根据给定的权值集合,找出最小的两个权值,构造一棵子树将这两个权值作为其孩子结点,二者权值之和作为根结点;(2)在原集合中删除这两个结点的权值,并引入根节点的权值;(3)重复步骤(1)和步骤(2),直到原权值集合为空。 8、二叉树的遍历:遍历是按某种策略访问树中的每个结点,且仅访问一次的过程。 (1)前序遍历:又称为先序遍历,按根 -> 左 -> 右的顺序进行遍历。 (2)后序遍历:按左 -> 右 -> 根的顺序进行遍历。 (3)中序遍历:按左 -> 根 -> 右的顺序进行遍历。 (4)层次遍历:按层次顺序进行遍历。 9、图的邻接矩阵表示:用一个n阶方阵R来存放图中各结点的关联信息,其矩阵素Rij定义为:
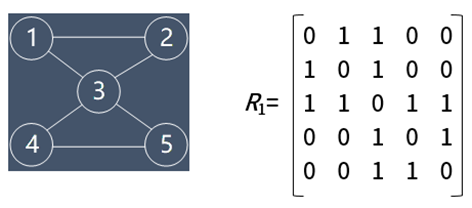
3、循环链表:队空条件:head=tail;队满条件:(tail+1)%size=head。 4、树的概念: (1)双亲、孩子和兄弟:结点的子树的根称为该结点的孩子;相应地,该结点称为其子结点的双亲。具有相同双亲的结点互为兄弟。 (这里涉及到2个层次,第一个层次的子树,这棵子树的根是第一层结点的孩子结点,第一层结点是其子节点的双亲节点/父节点)。 (2)结点的度:一个结点的子树的个数记为该结点的度 (3)叶子节点:也称为终端结点,指度为0的结点 (4)内部结点:指度不为0的结点,也称为分支节点或非终端节点。除根结点之外,分支结点也称为内部结点。 (5)结点的层次:根为第一层,根的孩子为第二层,依次类推,若某节点在第i层,则其孩子结点在第i+1层 (6)树的高度:一颗树的最大层次数记为树的高度(深度) 5、二叉树的重要特性: (1)在二叉树的第i层上最多有2i-1个结点(i≥1); (2)深度为k的二叉树最多有2k -1个结点(k≥1); (3)对任何一棵二叉树,如果其叶子结点数为n0,度为2的结点数为n2,则n0=n2+1。 (4)如果对一棵有n个结点的完全二叉树的结点按层序编号(从第1层到 L log2n ˩+1层,每层从左到右),则对任一结点i(1≤i≤n),有: 如果i=1,则结点i无父结点,是二叉树的根;如果i>1,则父结点是L i/2 ˩ ; 如果2i>n,则结点i为叶子结点,无左子结点;否则,其左子结点是结点2i; 如果2i+1>n,则结点i无右子叶点,否则,其右子结点是结点2i+1。 6、特殊的树: (1)二叉树:二叉树是每个结点最多有两个孩子的有序数,可以为空树,可以只有一个结点。 (2)满二叉树:任何结点,或者是树叶,或者恰有两棵非空子树。 (3)完全二叉树:最多只有最小面的两层结点的度可以小于2,并且最下面一层的结点全都集中在该层左侧的若干位置。 (4)平衡二叉树:树中任一结点的左右子树高度之差不超过1。 (5)查找二叉树:又称之为排序二叉树。任一结点的权值,大于其左孩子结点,小于其右孩子结点。 (6)线索二叉树:在每个结点中增加两个指针域来存放遍历时得到的前驱和后继信息。 (7)最优二叉树:又称为哈弗曼树,它是一类带权路径长度最短的树。 7、最优二叉树(哈弗曼树)的构造过程:(1)根据给定的权值集合,找出最小的两个权值,构造一棵子树将这两个权值作为其孩子结点,二者权值之和作为根结点;(2)在原集合中删除这两个结点的权值,并引入根节点的权值;(3)重复步骤(1)和步骤(2),直到原权值集合为空。 8、二叉树的遍历:遍历是按某种策略访问树中的每个结点,且仅访问一次的过程。 (1)前序遍历:又称为先序遍历,按根 -> 左 -> 右的顺序进行遍历。 (2)后序遍历:按左 -> 右 -> 根的顺序进行遍历。 (3)中序遍历:按左 -> 根 -> 右的顺序进行遍历。 (4)层次遍历:按层次顺序进行遍历。 9、图的邻接矩阵表示:用一个n阶方阵R来存放图中各结点的关联信息,其矩阵素Rij定义为:

 如:
如:

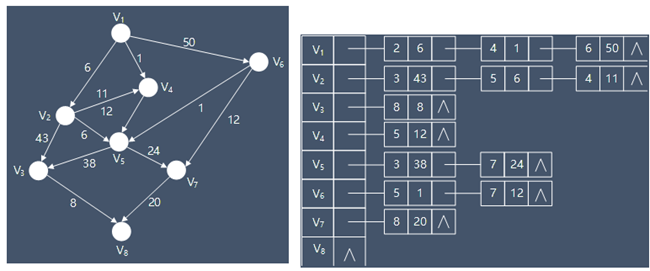
 10、图的邻接表表示:首先把每个顶点的邻接顶点用链表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。如:
10、图的邻接表表示:首先把每个顶点的邻接顶点用链表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。如:

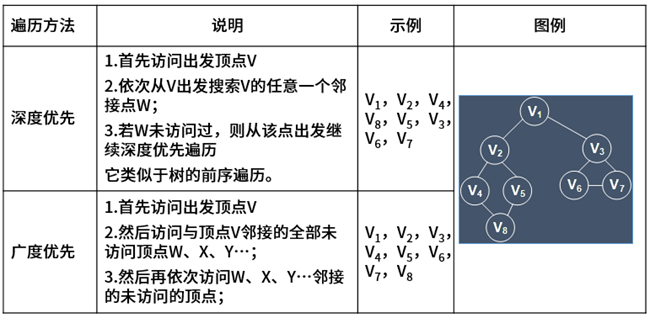
 11、图的遍历:
11、图的遍历:

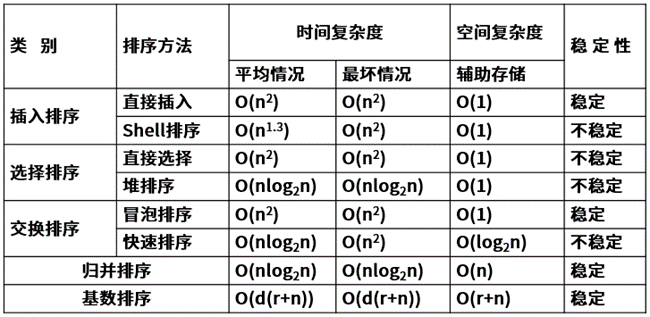
 12、图的拓扑排序:拓扑排序是将AOV网中的所有顶点排成一个线性序列的过程,并且该序列满足:若在AOV网点中从顶点Vi到Vj有一条路径,则在该线性序列中,顶点Vi必然在顶点Vj之前。 13、顺序查找的思想:将待查找的关键字为key的素从头到尾与表中素进行比较,如果中间存在关键字为key的素,则返回成功;否则,则查找失败。 14、A二分法查找的基本思想是:(设R[low,…,high]是当前的查找区) (1)确定该区间的中点位置:mid=L(low+high)/2˩; (2)将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下: 若R[mid].key>k,则由表的有序性可知R[mid,…,n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low,…,mid–1]中。因此,新的查找区间是左子表R[low,…,high],其中high=mid–1。 若R[mid].key<k,则要查找的k必在mid的右子表R[mid+1,…,high]中,即新的查找区间是右子表R[low,…,high],其中low=mid+1。 若R[mid].key=k,则查找成功,算法结束。 (3)下一次查找是针对新的查找区间进行,重复步骤(1)和(2)。 (4)在查找过程中,low逐步增加,而high逐步减少。如果high<low,则查找失败,算法结束。 折半查找在查找成功时关键字的比较次数最多为 L log2n +1 ˩ 次。 折半查找的时间复杂度为 O(log2n)次。 16、散列表查找的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关键字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0..n-1](n<<m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。 18、各种排序算法对比:
12、图的拓扑排序:拓扑排序是将AOV网中的所有顶点排成一个线性序列的过程,并且该序列满足:若在AOV网点中从顶点Vi到Vj有一条路径,则在该线性序列中,顶点Vi必然在顶点Vj之前。 13、顺序查找的思想:将待查找的关键字为key的素从头到尾与表中素进行比较,如果中间存在关键字为key的素,则返回成功;否则,则查找失败。 14、A二分法查找的基本思想是:(设R[low,…,high]是当前的查找区) (1)确定该区间的中点位置:mid=L(low+high)/2˩; (2)将待查的k值与R[mid].key比较,若相等,则查找成功并返回此位置,否则需确定新的查找区间,继续二分查找,具体方法如下: 若R[mid].key>k,则由表的有序性可知R[mid,…,n].key均大于k,因此若表中存在关键字等于k的结点,则该结点必定是在位置mid左边的子表R[low,…,mid–1]中。因此,新的查找区间是左子表R[low,…,high],其中high=mid–1。 若R[mid].key<k,则要查找的k必在mid的右子表R[mid+1,…,high]中,即新的查找区间是右子表R[low,…,high],其中low=mid+1。 若R[mid].key=k,则查找成功,算法结束。 (3)下一次查找是针对新的查找区间进行,重复步骤(1)和(2)。 (4)在查找过程中,low逐步增加,而high逐步减少。如果high<low,则查找失败,算法结束。 折半查找在查找成功时关键字的比较次数最多为 L log2n +1 ˩ 次。 折半查找的时间复杂度为 O(log2n)次。 16、散列表查找的基本思想是:已知关键字集合U,最大关键字为m,设计一个函数Hash,它以关键字为自变量,关键字的存储地址为因变量,将关键字映射到一个有限的、地址连续的区间T[0..n-1](n<<m)中,这个区间就称为散列表,散列查找中使用的转换函数称为散列函数。 18、各种排序算法对比:

 19、排序算法应用情景对比: (1)若待排序列的记录数目n较小,可采用直接插入排序和简单选择排序。由于直接插入排序所需的记录移动操作较简单选择排序多,因而当记录本身信息量大时,用简单选择排序方法较好。 (2)若待排记录按关键字基本有序,宜采用直接插入排序或冒泡排序。 (3)当n很大且关键字位数较少时,采用基数排序较好。 (4)若n很大,则应采用时间复杂度为O(nlog2n)的排序方法,例如快速排序、堆排序或归并排序: 快速排序目前被认为是内部排序中最好的方法,当待排序的关键字为随机分布时,快速排序的平均运行时间最短; 堆排序只需要一个辅助空间,并且不会出现在快速排序中可能出现的最快情况。 快速排序和堆排序都是不稳定的排序方法,若要求排序稳定,可选择归并排序。 20、常见的对算法执行所需时间的度量: O(1)<O(log2n)<O(n)<O(nlog2n)<O(n2)<O(n3)<O(2n) 21、常见算法逻辑的时间复杂度: (1)单个语句,或程序无循环和复杂函数调用:O(1) (2)单层循环:O(n);双层嵌套循环:O(n2);三层嵌套循环:O(n3)。 (3)树形结构、二分法、构建堆过程:O(log2n)。 (4)堆排序、归并排序:O(nlog2n)。 (5)所有不同可能的排列组合:O(2n)。 22、分治法:把一个问题拆分成多个小规模的相同子问题,一般可用递归解决。 23、动态规划法:划分子问题(最优子结构),并把子问题结果使用数组存储,利用查询子问题结果构造最终问题结果。 24、贪心法:局部最优,但整体不见得最优。每步有明确的,既定的策略。 25、回溯法:系统的搜索一个问题的所有解或任一解。有试探和回退的过程。 26、面向对象基本概念: 对象:属性(数据)+方法(操作)+对象ID 封装:隐藏对象的属性和实现细节,仅对外公开接口(信息隐藏技术) 类(实体类/控制类/边界类) 接口:一种特殊的类,他只有方法定义没有实现 继承与泛化:复用机制(单重继承和多重继承) 重置/覆盖(Overriding):在子类中重新定义父类中已经定义的方法 重载:一个类可以有多个同名而参数类型不同的方法 多态:不同对象收到同样的消息产生不同的结果 过载多态:同一个名字在不同的上下文中所代表的含义不同。 动态绑定:根据接收对象的具体情况将请求的操作与实现的方法进行连接(运行时绑定) 消息和消息通信:对象之间进行通信的一种构造叫做消息。消息是异步通信的(消息传递:接收到信息的对象经过解释,然后予以响应)
19、排序算法应用情景对比: (1)若待排序列的记录数目n较小,可采用直接插入排序和简单选择排序。由于直接插入排序所需的记录移动操作较简单选择排序多,因而当记录本身信息量大时,用简单选择排序方法较好。 (2)若待排记录按关键字基本有序,宜采用直接插入排序或冒泡排序。 (3)当n很大且关键字位数较少时,采用基数排序较好。 (4)若n很大,则应采用时间复杂度为O(nlog2n)的排序方法,例如快速排序、堆排序或归并排序: 快速排序目前被认为是内部排序中最好的方法,当待排序的关键字为随机分布时,快速排序的平均运行时间最短; 堆排序只需要一个辅助空间,并且不会出现在快速排序中可能出现的最快情况。 快速排序和堆排序都是不稳定的排序方法,若要求排序稳定,可选择归并排序。 20、常见的对算法执行所需时间的度量: O(1)<O(log2n)<O(n)<O(nlog2n)<O(n2)<O(n3)<O(2n) 21、常见算法逻辑的时间复杂度: (1)单个语句,或程序无循环和复杂函数调用:O(1) (2)单层循环:O(n);双层嵌套循环:O(n2);三层嵌套循环:O(n3)。 (3)树形结构、二分法、构建堆过程:O(log2n)。 (4)堆排序、归并排序:O(nlog2n)。 (5)所有不同可能的排列组合:O(2n)。 22、分治法:把一个问题拆分成多个小规模的相同子问题,一般可用递归解决。 23、动态规划法:划分子问题(最优子结构),并把子问题结果使用数组存储,利用查询子问题结果构造最终问题结果。 24、贪心法:局部最优,但整体不见得最优。每步有明确的,既定的策略。 25、回溯法:系统的搜索一个问题的所有解或任一解。有试探和回退的过程。 26、面向对象基本概念: 对象:属性(数据)+方法(操作)+对象ID 封装:隐藏对象的属性和实现细节,仅对外公开接口(信息隐藏技术) 类(实体类/控制类/边界类) 接口:一种特殊的类,他只有方法定义没有实现 继承与泛化:复用机制(单重继承和多重继承) 重置/覆盖(Overriding):在子类中重新定义父类中已经定义的方法 重载:一个类可以有多个同名而参数类型不同的方法 多态:不同对象收到同样的消息产生不同的结果 过载多态:同一个名字在不同的上下文中所代表的含义不同。 动态绑定:根据接收对象的具体情况将请求的操作与实现的方法进行连接(运行时绑定) 消息和消息通信:对象之间进行通信的一种构造叫做消息。消息是异步通信的(消息传递:接收到信息的对象经过解释,然后予以响应)
2024最新激活全家桶教程,稳定运行到2099年,请移步至置顶文章:https://sigusoft.com/99576.html
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请联系我们举报,一经查实,本站将立刻删除。
文章由激活谷谷主-小谷整理,转载请注明出处:https://sigusoft.com/42099.html